Matemtica Financeira Valor do Dinheiro no Tempo Matemtica


































![Funções Financeiras da HP 12 C [n]: abastece ou calcula o número de períodos Funções Financeiras da HP 12 C [n]: abastece ou calcula o número de períodos](https://slidetodoc.com/presentation_image/392b85938029e76f32c9fbe23b26956c/image-37.jpg)































































- Slides: 116

Matemática Financeira - Valor do Dinheiro no Tempo

Matemática Financeira Módulo A

Módulo A – Introdução a Matemática Financeira • Objetivo do Módulo: • Ao final deste módulo o aluno deve ser capaz de : • Compreender a importância do valor do dinheiro no tempo, da Matemática Financeira na vida das pessoas e das empresas. • Conceituar Taxa de Juros e Diagrama do Fluxo de Caixa e critérios de capitalização dos juros

Módulo A – Introdução a Matemática Financeira • - Porque estudar o Valor do Dinheiro no Tempo? • - Importância de se fazer um Planejamento Financeiro • - Porque estudar Matemática Financeira? • - Objetivos da Matemática Financeira

Módulo A – Introdução a Matemática Financeira • Preparação Prévia: - Leitura prévia do Texto 1 ou de qualquer capítulo de qualquer livro sobre o assunto

Módulo A – Introdução a Matemática Financeira • Organize sua vida financeira e descubra que possui mais recursos do que pensa ter para investir. • Faça um PLANEJAMENTO FINANCEIRO e responda: - Para onde vai o meu dinheiro? Por que investir? Mantenho minhas aplicações ou pago minhas dívidas? Como selecionar meus objetivos? Quais são as minhas opções de investimentos?

Exemplo: • Se um amigo lhe pedisse $ 1. 000, 00 para lhe pagar os mesmos $ 1. 000, 00 daqui a um ano, o que você acharia ? • Com certeza, por melhor que fosse seu amigo, a proposta não seria vista com bons olhos!!! • Alguns pontos vêm a mente: – Será que ele vai me pagar? – Será o poder de compra dos $ 1. 000, 00 daqui a um ano será o mesmo? – Se eu permanecesse com os $ 1. 00, poderia aplicá -los na poupança e ganhar rendimentos?

• Os pontos questionados remetem ao custo do dinheiro. • Ao transportar valores no tempo, existe um custo que pode ser decomposto em: – inflação – risco de crédito – taxa real de juros • Nunca some valores em datas diferentes

• Objetivos da Matemática Financeira - Transformar fluxos de caixa em outros equivalentes, com aplicação das taxas de juros de cada período, para se levar em consideração o valor do dinheiro no tempo. - Analisar e comparar diversas alternativas de fluxos de caixa para uma mesma operação.

• Fluxo de Caixa - Entradas e saídas de caixa de uma operação financeira ao longo do seu prazo de duração. • As operações financeiras precisam ser representadas pelos seus fluxos de caixa para poderem ser corretamente analisadas com os conceitos de matemática financeira. • As saídas de caixa correspondem aos pagamentos, têm sinais negativos e são representadas por setas apontadas para baixo. • As entradas de caixa correspondem aos recebimentos, têm sinais positivos e são representadas por setas apontadas para cima.

Fluxo de Caixa - Convenções Convenção de Final de Período Valores que ocorrem ao longo dos períodos são representados nos finais dos respectivos períodos. Unidades de Tempo Ano; Semestres; Trimestres; Meses e Dias

Valor do dinheiro no tempo • DEFINIÇÕES DE JUROS • - Remuneração do dinheiro aplicado. • - Custo do dinheiro tomado emprestado. • REGIMES DE JUROS • - Juros simples (Linear, Progressão Aritmética) • - Juros Compostos (Exponencial, Progressão Geométrica) • TAXAS DE JUROS • ___% a. d. (diárias) ___% a. a. (anuais) • ___% a. s. (semestrais) ___% a. t. (trimestrais) • ___% a. m. (mensais) • Taxa ( i ) e Número de Períodos ( n ) devem estar sempre na mesma base!!

Simbologia e Convenções Adotadas • • Final de período -Type =0 Início de período - Type = 1 Série postecipada (END) Série antecipada (BEGIN) n - Número de períodos de capitalização de juros; i - Taxa de juros em cada período, em %; PV - Valor presente, capital inicial aplicado; FV - Valor futuro, montante no final de n períodos; PMT - Pagamentos periódicos de mesmo valor que ocorrem no final (end) ou no início de cada período (begin)

Conceitos Gerais - Juros • “Juro (J) é a diferença entre o que foi emprestado no presente (PV) e o que é cobrado no período de tempo futuro (FV), quer seja ano, mês ou dia J = FV – PV J = PV. i

Conceitos Gerais - Juros • A Taxa percentual – refere-se aos “centos” do capital, ou seja, o valor dos juros para cada centésima parte do capital. • Ex: Um capital de $ 1. 000, aplicado a 20% ao ano rende juro, no final deste período de: Juro = 1000 / 100 x 20 = Juro = 10 x 20 = 200 = remuneração do capital investido.

Conceitos Gerais - Juros • A Taxa unitária – refere-se a unidade de capital. Reflete o rendimento de 0, 20 (20% / 100) por cada unidade de capital aplicada. • Ex: Um capital de $ 1. 000, aplicado a 20% ao ano rende juro, no final deste período de: Juro = 1000 x 20 / 100 = Juro = 1000 x 0, 20 = 200 = remuneração do capital investido.

Regimes de Juros • JUROS SIMPLES • Juros de cada período são sempre calculados sobre o capital inicial aplicado (principal). • Juros acumulados ao longo dos períodos não rendem apesar de ficarem retidos pela instituição financeira. • Crescimento do dinheiro, ao longo do tempo, é linear (ou em progressão aritmética • JUROS COMPOSTOS • Juros de cada período são calculados sobre o saldo existente no início do respectivo período. • Juros acumulados ao longo dos períodos, quando retidos pela instituição financeira, são capitalizados e passam a render juros. • Crescimento do dinheiro, ao longo do tempo, é exponencial ou em progressão geométrica).

Próximo Módulo: Trabalharemos – Juros Simples • Preparação Prévia: - Leitura prévia do Cap. 1 – do item 1. 8 até item 1. 11 da bibliografia básica - ou de qualquer livro sobre o assunto – Juros Simples

Matemática Financeira Módulo B

Módulo B – Juros Simples • Objetivo do Módulo: • Ao final deste módulo o aluno deve ser capaz de: • Desenvolver e aplicar a fórmula de juros simples, através de exercícios. • Conceituar – Montante e Capital • Compreender o significado de taxa proporcional, juro exato e comercial.

Módulo B – Juros Simples • Preparação Prévia: - Leitura prévia do Cap. 1 – do item 1. 8 até item 1. 11 da bibliografia básica - ou de qualquer capítulo de qualquer livro sobre o assunto – Juros Simples

Módulo B – Juros Simples • As parcelas adicionais são dadas por um valor proporcional ao capital inicial e ao tempo de aplicação Jn = PV. i. n FV = PV + Jn • Combinando as equações FV= PV. ( 1+ i. n ) • PV é o capital inicial; • FV é o montante no final do período n. • Jn são os juros acumulados até o final de n períodos de capitalização; • n é o número de períodos capitalizados; • i é a taxa de juros empregada por período de capitalização.

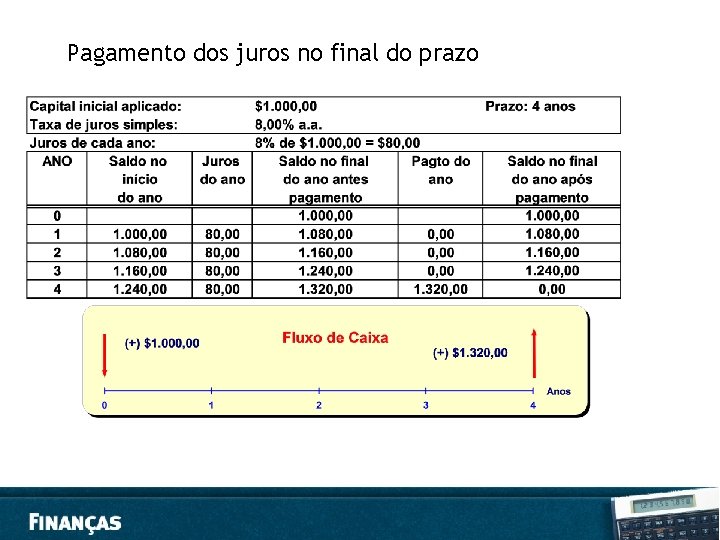
Exemplo - Juros Simples • Qual o montante equivalente a R$ 1. 000, 00 capitalizados a 8% ao ano em quatro anos? • Extrai-se do enunciado diretamente que PV = 1. 000, i = 8% ao ano e n = 4 anos. J = PV. i. n De outra forma: J = 1. 000× 0, 08× 4 = 320 FV = PV × (1+ i × n) FV = PV + J FV = 1. 000 × (1+0, 08× 4) FV = 1. 000 + 320 = 1. 320 FV = 1. 320, 00 Taxa ( i ) e Número de Períodos ( n ) devem estar sempre na mesma base!!

Pagamento dos juros no final do prazo


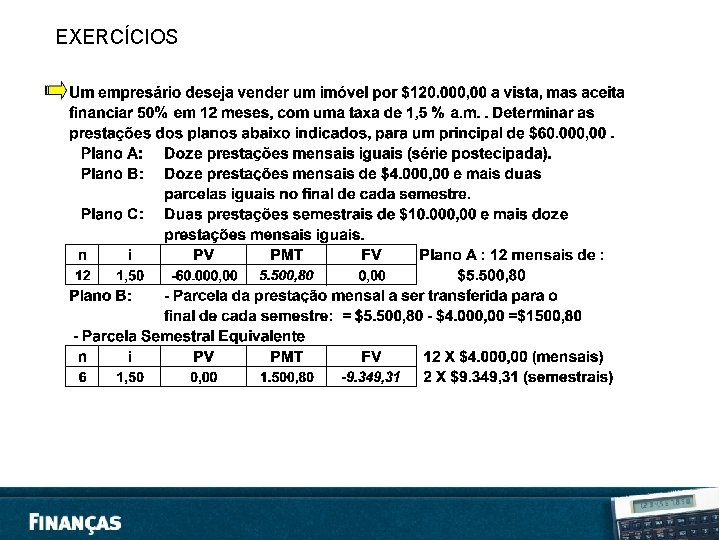
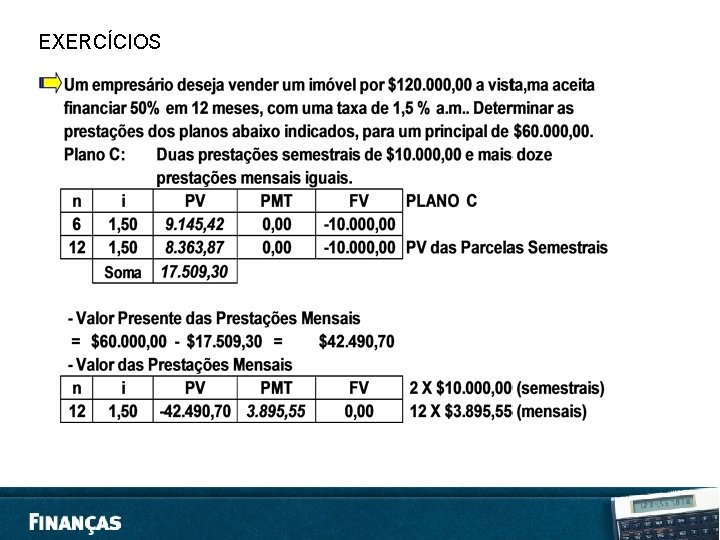
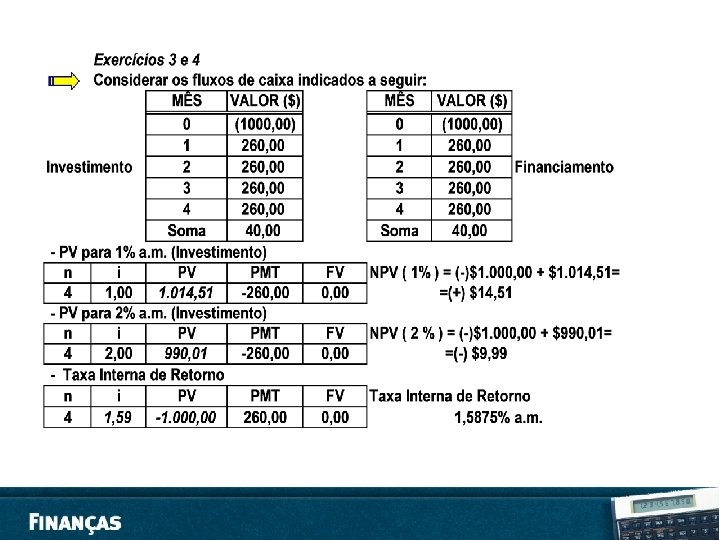
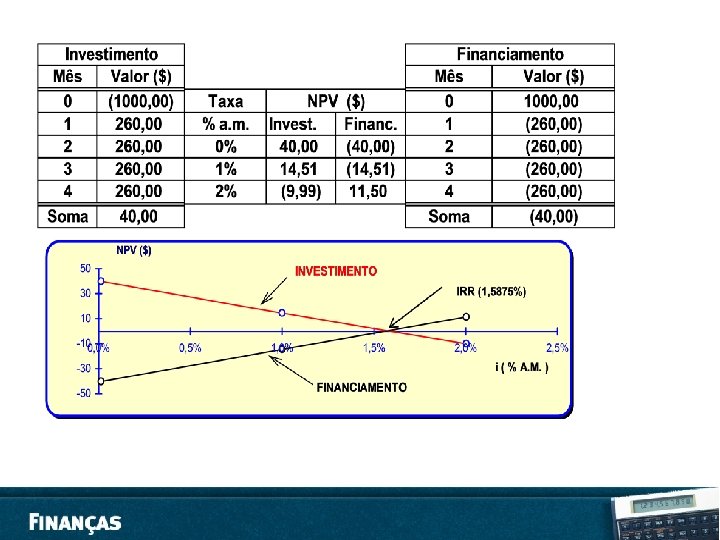
EXERCÍCIOS • 1. Que montante receberá um investidor que tenha aplicado R$ 280, 00 durante 15 meses, à taxa de 3% ao mês? • • SOLUÇÃO: O problema pede o valor resgatado (montante) e não os juros. Para isso basta adicionar os juros ao capital inicial. Assim, temos: VP = R$ 280, 00. . . . capital inicial ou principal n = 15 meses i = 3% a. m. = 0, 03 a. m. • Lembrando que VF = VP(1 + i n) vem: VF = 280, 00 (1 + 0, 03*15) = 280, 00 * 1, 45 = 406, 00, isto é, VF = R$ 406, 00 • Solução deste problema também pode ser obtida do seguinte modo: J = 280, 00 * 0, 03 * 15 = 126, 00 como VF = VP + J = 280, 00 + 126, 00 = 406, 00 ou seja VF = R$ 406, 00 • Com a CALCULADORA FINANCEIRA HP 12 C, temos: f FIN. . . limpa os dados registros financeiros f 2. . . estabelece o número de casas decimais 280 CHS PV. . . muda o valor atual para negativo e armazena em PV 3 ENTER 12 x i. . . Devemos entrar com a taxa em percentual ao ano (3% x 12) 15 ENTER 30 x n. . . Devemos entrar com o tempo em dias (15 x 30) f INT. . . Com este comando a calculadora apresentará, no visor, o valor dos juros: R$ 126, 00

EXERCÍCIOS • 1. Um investidor aplicou R$ 2. 500, 00 em Letras de Câmbio, por 60 dias, e, ao resgatá-las, após esse prazo, recebeu a quantia de R$ 2. 590, 00. – – • a. Quanto recebeu de juros? b. A que taxa esteve aplicado seu capital durante esse período? 2. Um industrial pediu um empréstimo de R$ 250. 000, 00 numa instituição financeira, por certo tempo. No dia em que foi liberado o empréstimo, pagou, antecipadamente, 22% de juros, conforme previa o contrato. – – a. Quanto pagou de juros? b. Se os juros foram retidos na data da liberação do empréstimo, qual foi a quantia efetivamente liberada? • 3. Um capital de R$ 80. 000, 00 ficou aplicado durante seis meses a 10% ao mês. Calcule o montante no fim de cada mês nos regimes de capitalização simples. • 4. Represente com um diagrama de fluxo de caixa as seguintes operações financeiras: – – – a. Uma aplicação de R$ 50. 000, 00 pela qual o investidor recebe R$ 80. 000, 00 após dois anos. b. A compra de um objeto, cujo preço a vista é R$ 30. 000, em 12 prestações mensais de R$ 2. 600, vencendo a primeira na data da compra. c. Depósitos de R$ 5. 000, 00 na Caderneta de Poupança, no fim de cada mês durante um ano, e retirada de R$ 61. 677, 81 dois meses após o último depósito.

EXERCÍCIOS 5. Qual o capital inicial para se ter um montante de R$ 148. 000, 00 daqui a 18 meses, a uma taxa de 48% ao ano, no regime de juro simples? Resp: 86. 047, 00. 6. Uma pessoa consegue um empréstimo de R$ 86. 400, 00 e promete pagar ao credor, após 10 meses, a quantia de R$ 116. 640, 00. Determine a taxa de juro anual cobrada? Resp: 42% ao ano. 7. Por quanto tempo deve ser aplicado o capital de R$ 800. 000, à taxa de juro de 16% ao ano, para obtermos um montante de R$ 832. 000, 00? Resp: 3 meses. 8. Uma loja vende toca-fitas por R$ 15, 00 à vista. A prazo, vende por R$ 16, 54 , sendo R$ 4, 00 de entrada e o restante após 4 meses. Qual é a taxa de juro mensal cobrada? Resp: 3, 5% ao mês.

Taxas de Juros -TAXAS PROPORCIONAIS Duas taxas são proporcionais quando os seus valores formam uma proporção direta com os tempos a elas referidos, reduzidos à mesma unidade. - Juro Exato Calendário do ano civil (365 dias) - Juro Comercial que admite o mês com 30 dias e o ano com 360 dias Sendo i a taxa de juro relativa a um período e ik a taxa proporcional queremos determinar, relativa à fração 1/k do período, temos: EXEMPLO: Calcule a taxa mensal proporcional a 30% ao ano? Lembrando que 1 ano = 12 meses, temos: • i 12 = 30/12 = 2, 5 isto é 2, 5% a. m.

• EXERCÍCIOS PROPOSTOS • 1. Transformar 2 anos, 3 meses e 12 dias em: a. Anos b. meses c. dias Resp: - 2, 28 anos; 27, 4 meses; 832 dias • 2. Qual a taxa anual proporcional a 1, 4% ao mês? Resp: - 16, 8% a. a. • 3. Calcular os juros de um investimento de R$ 2. 500, à taxa de 3% ao mês, pelo prazo de 1 ano, 4 meses e 10 dias. Resp: - R$ 1. 225, 00 • 4. Um investimento de R$ 2. 800, 00 rendeu em 1 ano, 5 meses e 3 dias a importância de R$ 2. 872, 80. Calcular a taxa mensal dessa rentabilidade. Resp: - 6% a. m. • 5. Que quantia deve-se investir à taxa de 3% a. m. , para que se tenha ao final de 1 ano, 4 meses e 6 dias uma renda de R$ 97. 200, 00? Resp: - R$ 200. 000, 00 • 6. Calcular os juros e o montante de uma aplicação de R$ 200. 000, 00 a 4, 8% a. m. , pelo prazo de 2 anos, 3 meses e 12 dias. Resp: - R$ 263. 040, 00 e R$ 463. 040, 00 • 7. Um investidor aplica 2/5 de seu capital a 3, 5% a. m. e o restante a 24% ao semestre. Decorridos 2 anos, 3 meses e 15 dias, recebe um total de R$ 313. 500, 00 de juros. Calcular o seu capital. Resp: - R$ 300. 000, 00

Matemática Financeira Módulo C

Módulo C – Juros Compostos • Objetivo do Módulo: • Ao final deste módulo o aluno deve ser capaz de: • Desenvolver e aplicar a fórmula de juros compostos, através de exercícios. • Conceituar – Taxa Nominal e Efetiva • Compreender o significado de taxas equivalentes.

Juros Compostos • Juros são incorporados ao capital, e os juros para o próximo período calculados sobre o novo capital • Método mais empregado por instituições bancárias e financiadoras FV = PV x (1+i)n • n é o número de períodos capitalizados; • PV é o capital inicial; • FV é o capital disponível ou exigível no final do período n, ou montante; • i é a taxa de juros empregada por período de capitalização.

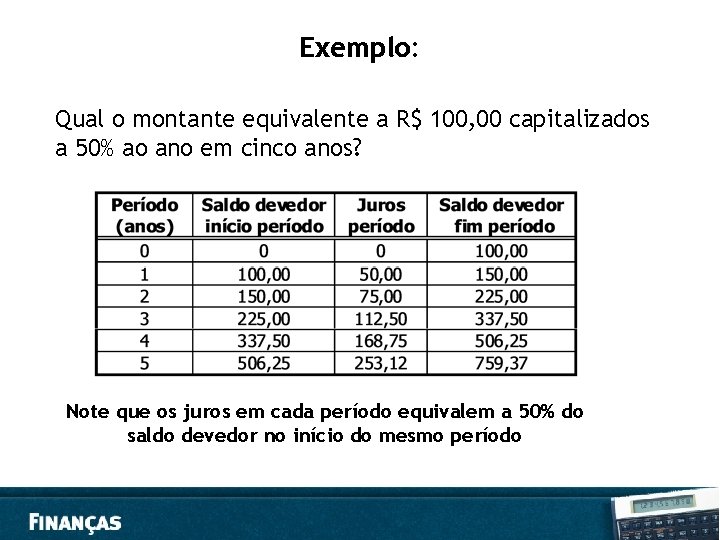
Exemplo: Qual o montante equivalente a R$ 100, 00 capitalizados a 50% ao ano em cinco anos? Note que os juros em cada período equivalem a 50% do saldo devedor no início do mesmo período

Aplicando a fórmula: • Suponha que você coloque $1. 000 (VP) numa aplicação rendendo uma taxa de juros (i) de 10% a. a. A quantia que você terá daqui a cinco anos, assumindo que você não sacou nada da conta antes disso, é chamada valor futuro (VF). Taxa ( i ) e Número de Períodos ( n ) devem estar sempre na mesma base!! Seu valor futuro no final do ano 5 seria, então: VF = VP x (1 + i)n = VF = 1. 000 x (1 + 0, 10)5 VF = 1. 000 x 1, 61051 => Fator de capitalização VF = 1. 610, 51

Fórmulas de Juros Compostos VP = VF = VP(1 + i ) n VF (1 + i )n 1 n VF - = æ VF ö n = ÷ 1 i 1 ç VP è VP ø æ VF ö log ç ÷ è VP ø n= log(1 + i )
![Funções Financeiras da HP 12 C n abastece ou calcula o número de períodos Funções Financeiras da HP 12 C [n]: abastece ou calcula o número de períodos](https://slidetodoc.com/presentation_image/392b85938029e76f32c9fbe23b26956c/image-37.jpg)
Funções Financeiras da HP 12 C [n]: abastece ou calcula o número de períodos [i]: abastece ou calcula a taxa de juros [PV]: abastece ou calcula o Valor Presente [PMT]: abastece ou calcula a Prestação [FV]: abastece ou calcula o Valor Futuro

VF = VP x (1 + i)n = VF = 2. 000 x (1 + 0, 01)24 VF = 2. 000 x 1, 261973 VF = 2. 539, 47

VP = VF / (1 + 0, 0125)24 VP = 1. 000 / 1, 34735 VP = 742, 20

VF = VP x (1 + i)n = VF = (1 + i)1/n VP 1. 150 = (1 + i)1/10 = 1, 151/10 = ((1 + i)1/10 1. 000 1, 0140743 = 1 + i I = 0, 0140743 * 100 = 1, 40743% a. m.

VF = VP x (1 + i)n = VF = (1 + i)1/n VP log VF n =. VP = log (1 + 0, 06) n = 0, 30103. = 11, 89 anos 0, 02531

Taxas de Juros

Taxas de Juros -TAXAS EQUIVALENTES • Duas taxas são equivalentes quando, aplicadas a um mesmo capital, durante o mesmo período, produzem o mesmo juro. EXEMPLO: Calcular o juro produzido pelo capital de R$ 20. 000, 00 à taxa de 4% ao mês, durante 6 meses à taxa de 12% ao trimestre, durante 2 trimestres SOLUÇÃO • No primeiro caso, temos J = 20. 000, 00 x 0, 04 x 6 = 4. 800, 00 • No segundo caso, temos J = 20. 000, 00 x 0, 12 x 2 = 4. 800, 00 • Como os juros são iguais, podemos dizer que: 4% a. m. e 12% a. t. , são taxas equivalentes

Taxas de Juros





Matemática Financeira Módulo D

Módulo D – Desconto • Objetivo do Módulo: • Ao final deste módulo o aluno deve ser capaz de: • Desenvolver e aplicar as fórmulas de desconto Comercial - “por fora” e desconto Racional - “por dentro” • Definir Valor Nominal e Valor Atual.

DESCONTO • Se uma pessoa deve uma quantia em dinheiro numa data futura, é normal que entregue ao credor um título de crédito, que é o comprovante dessa dívida. Todo título de crédito tem uma data de vencimento; porém, o devedor pode resgatá-lo antecipadamente, obtendo com isso um abatimento denominado desconto. • O desconto é uma das mais comuns aplicações da regra de juro. • Os títulos de crédito mais utilizados em operações financeiras são a nota promissória, a duplicata e a letra de câmbio.

• A nota promissória é um comprovante da aplicação de um capital com vencimento predeterminado. É um título muito usado entre pessoas físicas ou entre pessoa física e instituição financeira. • A duplicata é um título emitido por uma pessoa jurídica contra seu cliente (pessoa física ou jurídica), para o qual ela vendeu mercadorias a prazo ou prestou serviços a serem pagos no futuro, segundo um contrato. • A letra de câmbio, assim como a nota promissória, é um comprovante de uma aplicação de capital com vencimento predeterminado; porém, é um título ao portador, emitido exclusivamente por uma instituição financeira.

• As operações anteriormente citadas são denominadas operações de desconto, e o ato de efetuá-las é chamado descontar um título. Além disso: dia do vencimento é o dia fixado no título para pagamento (ou recebimento) da aplicação; • valor nominal (VN ) (ou valor futuro ou valor de face ou valor de resgate) é o valor indicado no título (importância a ser paga no dia do vencimento); • valor atual (VA) é o líquido pago (ou recebido) antes do vencimento: VA = VN - desconto • tempo ou prazo é o número de dias compreendido entre o dia em que se negocia o título e o de seu vencimento, incluindo o primeiro e não o último, ou então, incluindo o último e não o primeiro.

DESCONTO (d) é a quantia a ser abatida do valor nominal, isto é, a diferença entre o valor nominal e o valor atual : d = VN - VA. • O desconto pode ser feito considerando-se como capital o valor nominal ou valor atual. No primeiro caso, é denominado desconto comercial; no segundo, desconto racional.

• DESCONTO BANCÁRIO • Chamamos de desconto comercial, bancário ou por fora o equivalente ao juro simples produzido pelo valor nominal do título no período de tempo correspondente e à taxa fixada. • Sejam d o valor de desconto comercial, VN o valor nominal do título, VA o valor atual comercial, n o tempo que falta para o vencimento e i a taxa de desconto, então: d = VN. i. n • O valor atual bancário é dado por: VA = VN (1 – i. n)

EXERCÍCIOS 1. Um título de R$ 60. 000, 00 vai ser descontado à taxa de 2, 1% ao mês. Faltando 45 dias para o vencimento do título, determine: a. o valor do desconto comercial b. o valor atual comercial • Solução dados : VN = 60. 000, 00 i = 2, 1% a. m. n = 45 dias • a. d = VN. i. n = 60. 000 x 0, 021 x 1, 5 (um mês e meio) = d = R$ 1. 890, 00 • b. VA = VN – d VA = 60. 000 – 1. 890 = R$ 58. 110, 00 VA = R$ 58. 110, 00

• DESCONTO RACIONAL • Chamamos de desconto racional ou por dentro o equivalente ao juro produzido pelo valor atual do título numa taxa fixada e durante o tempo correspondente. • VA =. VN. (1 + i. n) Onde d (desconto racional) é igual : • d = VN - VA

• EXERCÍCIOS • 1. Um título de R$ 60. 000, 00 vai ser descontado à taxa de 2, 1% ao mês. Faltando 45 dias para o vencimento do título, determine: • a. o valor atual racional • b. o valor do desconto racional • SOLUÇÃO • VN = R$ 60. 000, 00 i = 2, 1% a. m. = 0, 021 a. m. n = 45 dias = 1, 5 meses • a. VA =. 60. 000. ( 1 + 0, 021. 1, 5) VA = 58. 167, 72 • b. d = VN – VA d = 60. 000 – 58. 167, 72 d = 1. 832, 28

Matemática Financeira Módulo E

Módulo E – Fluxo de Caixa – Série de Pagamentos - PMT • Objetivo do Módulo: • Ao final deste módulo o aluno deve ser capaz de: - Desenvolver e entender a importância da Matemática Financeira nos fluxos de caixa, permitindo o correto entendimento e uso de seus resultados. - Equivalência de dois ou mais capitais.

Fluxo de Caixa Representa uma série de pagamentos ou de recebimentos que se estima ocorrer em determinado intervalo de tempo. - Podem ser verificados das mais variadas formas e tipos em termos de períodos de ocorrência: 1. Quanto ao número de prestações: Finitas: quando ocorrem durante um período pré-determinado de tempo 2. Quanto à periodicidade dos pagamentos: Periódicas: quando os pagamentos ocorrem a intervalos constantes Não periódicas: quando os pagamentos ou recebimentos acontecem em intervalos irregulares de tempo

Fluxo de Caixa 3. Quanto ao valor das prestações: Uniformes: quando as prestações ou anuidades são iguais. Não uniformes: quando os pagamentos ou recebimentos apresentam valores distintos. Não Uniformes: quando os pagamentos ou recebimentos apresentam valores distintos. 4. Quanto ao prazo de pagamentos: Postecipadas: quando as anuidades iniciam após o final do primeiro período Antecipadas: quando o primeiro pagamento ocorre na entrada, no início da série

Fluxo de Caixa 5. Quanto ao primeiro pagamento: Diferidas: ou com carência, quando houver um prazo maior que um período entre a data do recebimento do financiamento e a data de pagamento da primeira prestação. Não Diferidas: quando não existir prazo superior a um período entre o início da operação e o primeiro pagamento ou recebimento

Equivalência Financeira e Fluxos de Caixa A Equivalência Financeira esta presente nas tomadas de decisões financeiras, pois seus resultados define os melhores planos de empréstimos; financiamentos mais atraentes; em propostas de refinanciamento e reescalonamento de dívidas; etc. Definição: dois ou mais fluxos de caixa são equivalentes quando produzem idênticos valores presentes (PV) num mesmo momento, convencionando-se determinada taxa de juros.

Fórmula para séries uniformes PMT = PV i ( 1 + i )n -1 Onde: PMT = Pagamento periódico igual n = número de pagamentos PV = Valor Presente i = taxa de juros

Fórmula para séries uniformes FV = PMT [ ( 1 + i )n - 1 ] i Onde: PMT = Pagamento periódico igual n = número de pagamentos FV = Valor Futuro i = taxa de juros

Fórmula para séries uniformes i(1 + i ) m ( ) × + PMT = PV 1 i n (1 + i) - 1 n Onde: PMT = Pagamento periódico igual m = carência em número de períodos n = número de pagamentos PV = Valor Presente i = taxa de juros

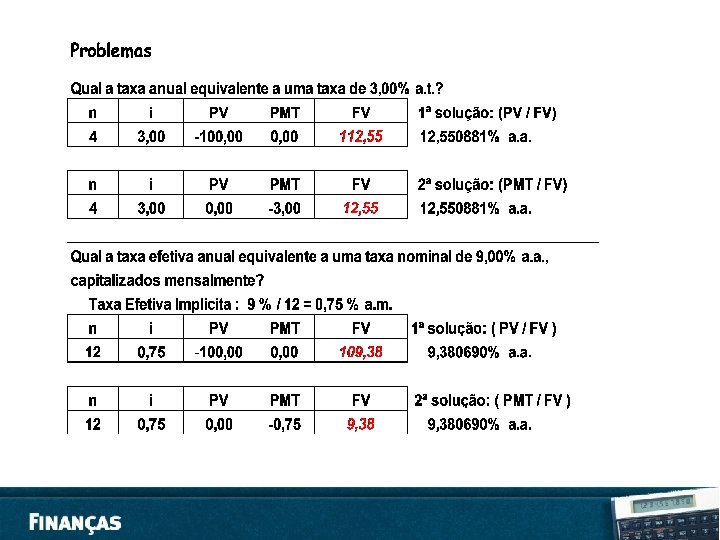
EXERCÍCIOS

EXERCÍCIOS

EXERCÍCIOS

EXERCÍCIOS

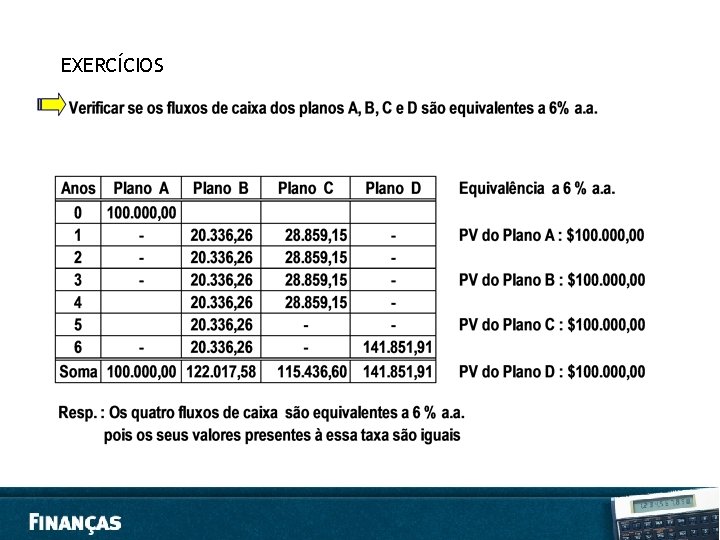
EXERCÍCIOS

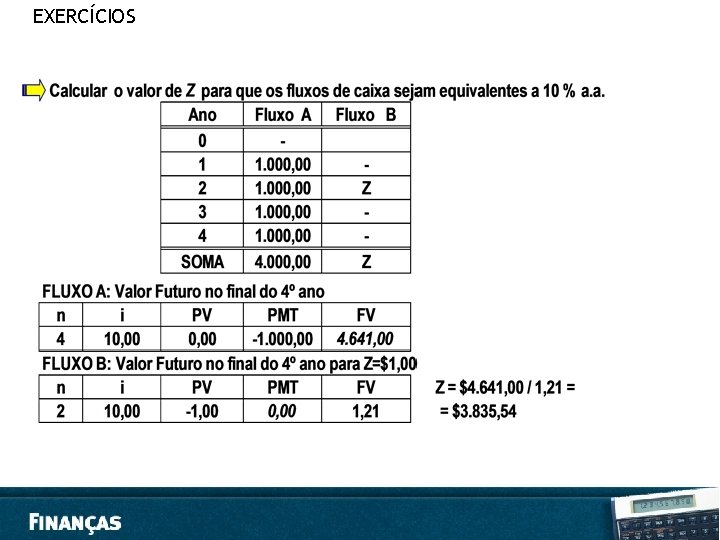
EXERCÍCIOS

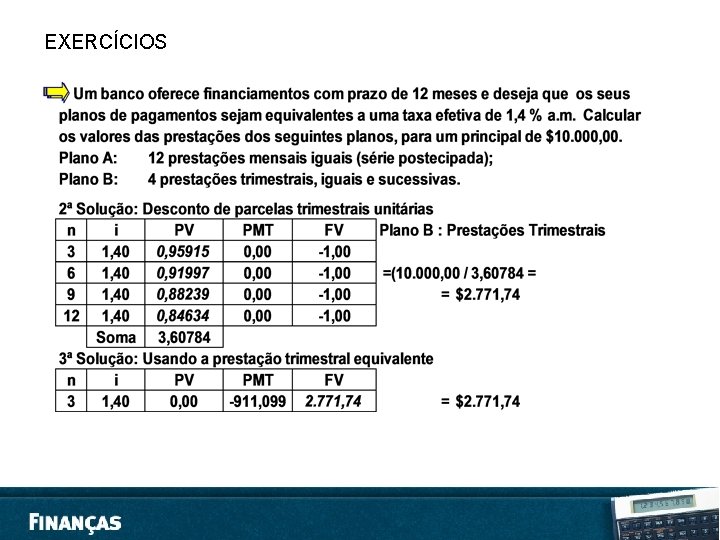
EXERCÍCIOS

EXERCÍCIOS

FLUXOS DE CAIXA MÚLTIPLOS Até agora temos considerado problemas que envolvem apenas um único fluxo de caixa, também chamado de pagamentos simples, isto é, restringimos a nossa atenção ao valor futuro de uma única quantia no presente ou o valor presente de um único fluxo de caixa futuro. Obviamente, isso limita bastante. Afinal de contas, a maioria dos investimentos do mundo real envolve muitos fluxos de caixa ao longo do tempo. Quando existirem muitos pagamentos, você ouvirá as pessoas de negócios se referirem a uma série de fluxos de caixa.

FLUXOS DE CAIXA MÚLTIPLOS Imagine que você espera comprar um computador em 2 anos depositando hoje numa aplicação que paga 8% a. a. de juros, o valor de $1. 200, e outros $ 1. 400 daqui a 1 ano. Quanto você deverá gastar no computador nesses dois anos? Essas figuras de linha do tempo são muito úteis para resolver problemas complexos. Toda vez que você encontrar dificuldades com um problema, desenhe a linha do tempo, que geralmente lhe ajudará a entender o que está passando.

EXERCÍCIOS 1. Suponhamos que a compra do computador possa ser adiada por mais 1 ano e que você consiga fazer um terceiro depósito de $ 1. 000 no final do segundo ano. Quanto estará disponível para gastar de agora a 3 anos? Resp: $ 4. 224, 61 2. Você acha que será capaz de depositar $ 4. 000 ao final de cada um dos três próximos anos em uma aplicação bancária que rende 8% de juros. Atualmente, você possui $ 7. 000 nessa aplicação. Quanto você terá em três anos? E em quatro? Resp: $ 21. 803, 58 e $23. 547, 87 3. Considere um investimento de $ 2. 000 ao final de cada ano durante os próximos cinco anos. O saldo atual é zero e a taxa é de 10% a. a. Calcule o valor futuro deste investimento, desenhando a linha do tempo. 4. Se você aplicar $ 100 daqui a um ano, $ 200 daqui a dois anos e $ 300 daqui a três anos, quanto você terá em três anos? Quanto deste montante é representado por juros? Quanto você terá em cinco anos se não realizar nenhuma aplicação adicional? Suponha uma taxa de juros igual a 7% durante o período. Resp: $ 628, 49; $ 719, 56 5. Monte todos estes exercícios anteriores numa planilha Excel e resolva-os por meio dela.

Matemática Financeira Módulo F

Coeficiente de Financiamentos É muito comum quando compramos à prestação, ou fazemos qualquer tipo de financiamento, surgir um fator financeiro constante que, ao multiplicar-se pelo valor presente do financiamento, apura as prestações. Financiamento x Coeficiente Financeiro = Prestações O coeficiente financeiro nada mais é do que o inverso do fator de valor presente. – Ele é muito utilizado no CDC – Crédito Direto ao Consumidor, no Arrendamento Mercantil (Leasing), financiamento de veículos e de eletrodomésticos. • Se quisermos encontrar o coeficiente de financiamento na HP-12 C, fazemos assim: 1 CHS PV Taxa i Nn

Coeficiente de Financiamentos EXEMPLO Admita que uma instituição financeira divulgue que seu coeficiente financeiro a ser liquidado em 6 prestações mensais, iguais e sucessivas, atinge 0, 189346 (seis casas decimais, geralmente). a. Qual o valor das prestações de um financiamento de $ 16. 000? b. Qual a taxa de juros? Solução Financiamento x Coeficiente Financeiro = Prestações a. PMT = 16. 000 x 0, 189346 = 3. 029, 54 b. . . 3, 77% a. m. 16000 CHS PV 3029, 54 PMT 6 n Encontrar i

Coeficiente de Financiamentos EXERCÍCIOS 1. Construir o coeficiente de financiamento de um contrato envolvendo 15 prestações mensais, iguais e sucessivas, a uma taxa de juros de 3, 5% a. m. Resp: 0, 086825 2. Uma empresa está avaliando o custo de determinado financiamento. Para tanto, identificou as seguintes condições em dois bancos: a. Coeficiente = 0, 119153, pagamento = 10 prestações mensais, iguais e sucessivas b. Coeficiente = 0, 307932, pagamento = 4 prestações, trimestrais, iguais e sucessivas. Determinar a proposta que apresenta o menor custo mensal.

Coeficiente de Financiamentos Perpetuidades Esta série ou anuidade se chama assim porque os fluxos de caixa são perpétuos. Por esta razão, obviamente, não podemos avaliá-las descontando todos os fluxos de caixa e nem tão pouco aplicando a fórmula diretamente. Felizmente, a avaliação é extremamente simples, e isto pode ser visto com um pouquinho de matemática. No caso de uma perpetuidade, temos:

Coeficiente de Financiamentos Perpetuidades – Exemplo: Suponha que a Fellini Co. queira emitir ações preferenciais a um preço de $100 por ação. Uma emissão, já realizada, muito semelhante de ações preferenciais obteve um preço de $40 por ação, mediante uma oferta de dividendos trimestrais de $ 1. Qual é o dividendo que a Fellini deveria oferecer, se suas ações preferenciais fossem emitidas? Solução A emissão que já ocorreu possui um valor presente de $ 40 e um fluxo de caixa trimestral de $ 1 para sempre. Como é uma perpetuidade: VP = PGTO i. i= 1. 40 i = 0, 025 * 100 = 2, 5% a. t. Para ser competitiva, a nova emissão da Fellini também deverá oferecer um rendimento trimestral de 2, 5%; portanto, para que o valor presente seja $ 100, os dividendos precisam ser iguais a $ 2, 5 por trimestre. • Atividade Resolver Estudo de Caso – material do programa deste módulo

Sistemas de Financiamento Sistema de Amortização Americano Sistema de Amortização Francês ou Tabela Price (TP) Sistema de Amortização Constante (SAC)

Sistemas de Financiamento Nem sempre as empresas possuem capital próprio para investir em um dado projeto Oportunidades não esperarão que a empresa poupe o suficiente para investir. Como consequência, as empresas terão de lançar mão de empréstimos. Debate sobre o texto Sistemas de Amortização

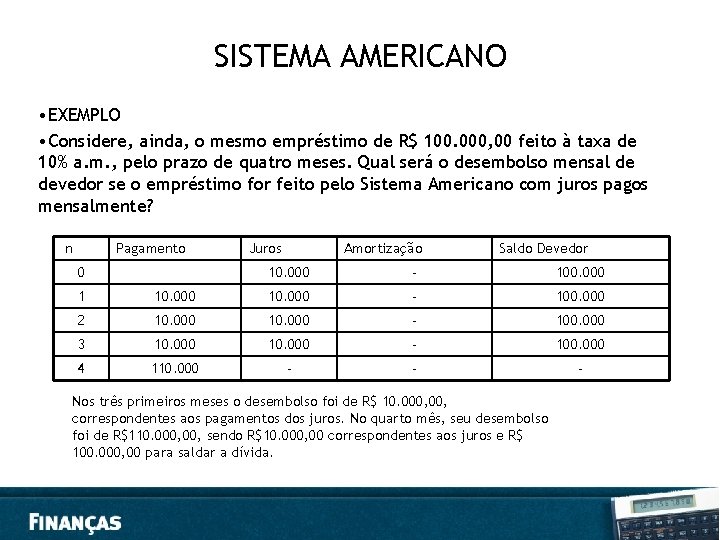
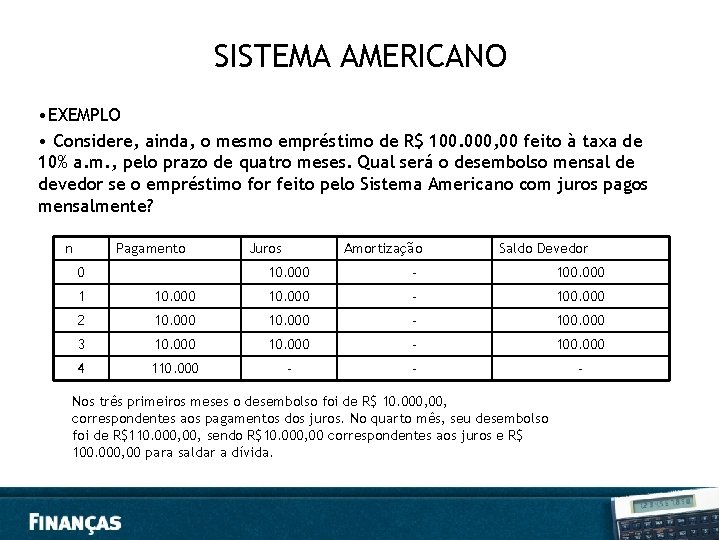
SISTEMA AMERICANO Por esse sistema, o devedor paga os juros periodicamente; o valor emprestado é pago no final do prazo estipulado para o empréstimo. Chamando de VP o valor emprestado à taxa i, os juros pagos em cada período são iguais e calculados como: Juros = VP. i Terminado o prazo, o devedor, no último pagamento, além dos juros, paga o capital emprestado (VP).

SISTEMA AMERICANO • EXEMPLO • Considere, ainda, o mesmo empréstimo de R$ 100. 000, 00 feito à taxa de 10% a. m. , pelo prazo de quatro meses. Qual será o desembolso mensal de devedor se o empréstimo for feito pelo Sistema Americano com juros pagos mensalmente? n Pagamento 0 Juros Amortização Saldo Devedor 10. 000 - 100. 000 1 10. 000 - 100. 000 2 10. 000 - 100. 000 3 10. 000 - 100. 000 4 110. 000 - - - Nos três primeiros meses o desembolso foi de R$ 10. 000, correspondentes aos pagamentos dos juros. No quarto mês, seu desembolso foi de R$110. 000, sendo R$10. 000, 00 correspondentes aos juros e R$ 100. 000, 00 para saldar a dívida.

SISTEMA AMERICANO • EXEMPLO • Considere, ainda, o mesmo empréstimo de R$ 100. 000, 00 feito à taxa de 10% a. m. , pelo prazo de quatro meses. Qual será o desembolso mensal de devedor se o empréstimo for feito pelo Sistema Americano com juros pagos mensalmente? n Pagamento 0 Juros Amortização Saldo Devedor 10. 000 - 100. 000 1 10. 000 - 100. 000 2 10. 000 - 100. 000 3 10. 000 - 100. 000 4 110. 000 - - - Nos três primeiros meses o desembolso foi de R$ 10. 000, correspondentes aos pagamentos dos juros. No quarto mês, seu desembolso foi de R$110. 000, sendo R$10. 000, 00 correspondentes aos juros e R$ 100. 000, 00 para saldar a dívida.

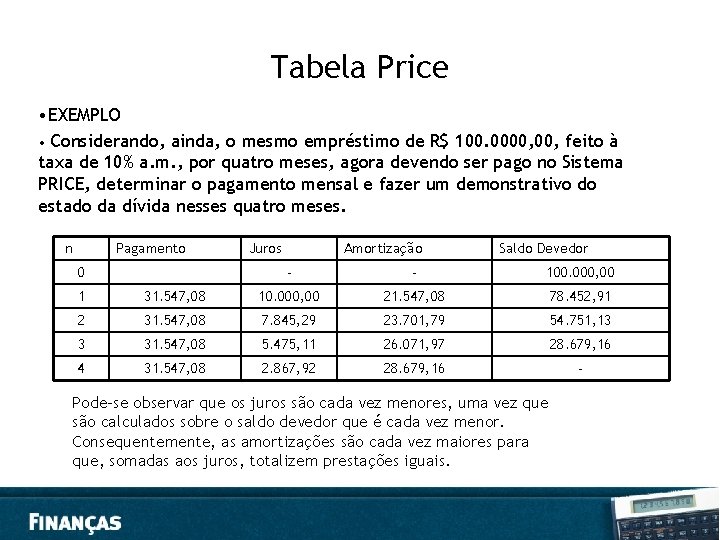
Tabela Price SISTEMA PRICE, FRANCÊS OU DE PRESTAÇÕES CONSTANTES Por esse sistema, o devedor paga o empréstimo em prestações iguais imediatas, incluindo, em cada uma, uma amortização parcial do empréstimo e os juros sobre o saldo devedor. O número de prestações varia em cada contrato. Suponha-se o empréstimo VP, feito à taxa i para ser pago em n prestações, pelo sistema PRICE - Método mais empregado no Brasil - Pagamento em Parcelas Constantes - Cálculo da Parcela: - Expressão da Série Anual Uniforme PMT = PV (( i (1+i)n ) / ((1+i)n – 1))

Tabela Price • EXEMPLO • Considerando, ainda, o mesmo empréstimo de R$ 100. 0000, feito à taxa de 10% a. m. , por quatro meses, agora devendo ser pago no Sistema PRICE, determinar o pagamento mensal e fazer um demonstrativo do estado da dívida nesses quatro meses. n Pagamento 0 Juros Amortização Saldo Devedor - - 100. 000, 00 1 31. 547, 08 10. 000, 00 21. 547, 08 78. 452, 91 2 31. 547, 08 7. 845, 29 23. 701, 79 54. 751, 13 3 31. 547, 08 5. 475, 11 26. 071, 97 28. 679, 16 4 31. 547, 08 2. 867, 92 28. 679, 16 - Pode-se observar que os juros são cada vez menores, uma vez que são calculados sobre o saldo devedor que é cada vez menor. Consequentemente, as amortizações são cada vez maiores para que, somadas aos juros, totalizem prestações iguais.

Sistema de Amortização Constante - SAC Pelo fato de a amortização ser constante, a série de pagamentos não é uniforme! O seguinte procedimento é tomado: Calculam-se inicialmente as amortizações: Amort = PV / n Calcula-se o saldo devedor em todos os anos SD = PV - Amort Calcula-se os juros, sobre o saldo devedor: Juros = PV. i

Sistema de Amortização Constante - SAC Considerando, mais uma vez, o mesmo empréstimo de R$100. 0000, feito à taxa de 10% a. m. , por quatro meses, agora devendo ser pago no sistema SAC, fazer um demonstrativo do estado da dívida nesses quatro meses. n Pagamento 0 Juros Amortização Saldo Devedor - - 100. 000, 00 1 35. 000, 00 10. 000, 00 25. 000, 00 75. 000, 00 2 32. 500, 00 7. 500, 00 25. 000, 00 50. 000, 00 3 30. 000, 00 5. 000, 00 25. 000, 00 4 27. 500, 00 2. 500, 0 25. 000, 00 - Pode-se observar que os juros são cada vez menores, uma vez que são calculados sobre o saldo devedor que é cada vez menor. Consequentemente, as amortizações sendo iguais, que somadas aos juros, totalizem prestações decrescentes.

Carência Acordo entre tomador de empréstimo e financiador, habilitando que, durante um certo período de tempo, apenas os juros sejam cobrados, sem pagamento de amortização. Quando se atinge o fim da carência, o empréstimo é quitado através de algum método pré-determinado dois tipos de carência são abordados: Caso 1 - Durante o prazo de carência, apenas os juros sobre o principal são devidos Caso 2 - Durante o prazo de carência, não há pagamento nenhum; nem de juros sobre o saldo devedor, nem de amortização do principal. Dessa forma, os juros são somados ao saldo devedor, resultando um saldo devedor maior.

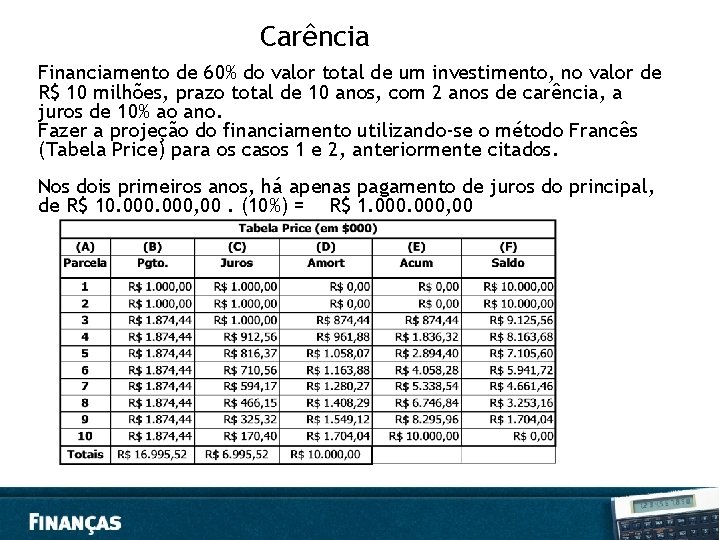
Carência Financiamento de 60% do valor total de um investimento, no valor de R$ 10 milhões, prazo total de 10 anos, com 2 anos de carência, a juros de 10% ao ano. Fazer a projeção do financiamento utilizando-se o método Francês (Tabela Price) para os casos 1 e 2, anteriormente citados. Nos dois primeiros anos, há apenas pagamento de juros do principal, de R$ 10. 000, 00. (10%) = R$ 1. 000, 00

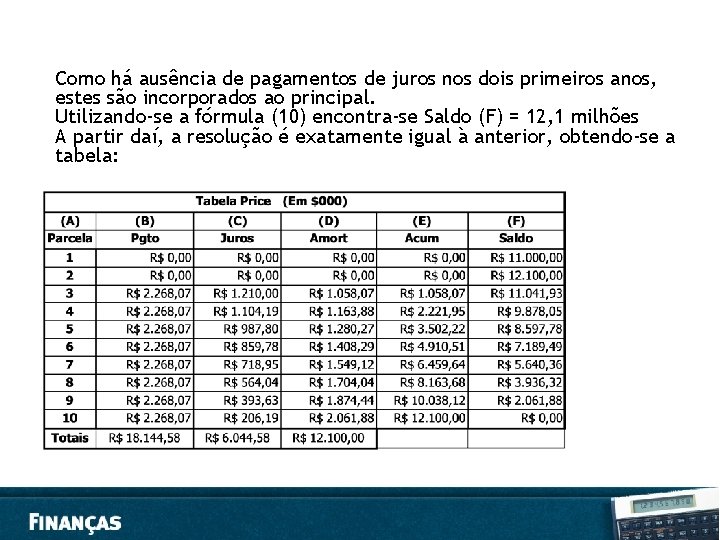
Como há ausência de pagamentos de juros nos dois primeiros anos, estes são incorporados ao principal. Utilizando-se a fórmula (10) encontra-se Saldo (F) = 12, 1 milhões A partir daí, a resolução é exatamente igual à anterior, obtendo-se a tabela:

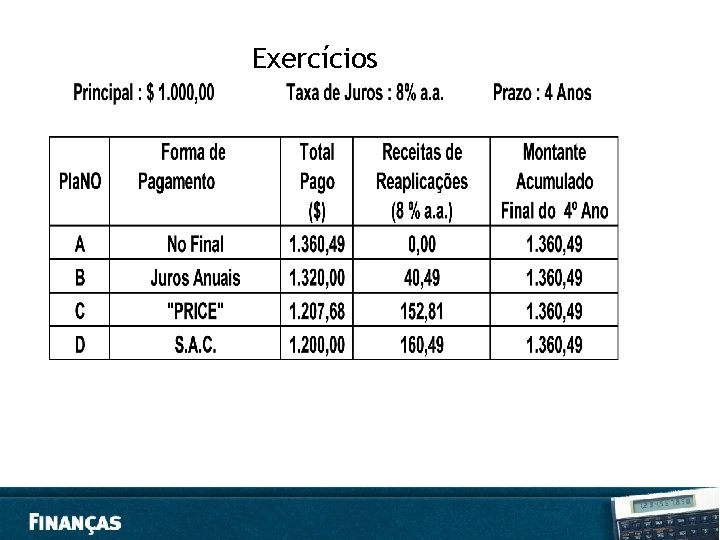
Exercícios

Matemática Financeira Módulo G

Valor presente, Equivalência e Taxa Interna de Retorno • Objetivos: – Discutir os principais aspectos relacionados às séries não uniformes – Avaliação de séries com base em: • VPL • TIR

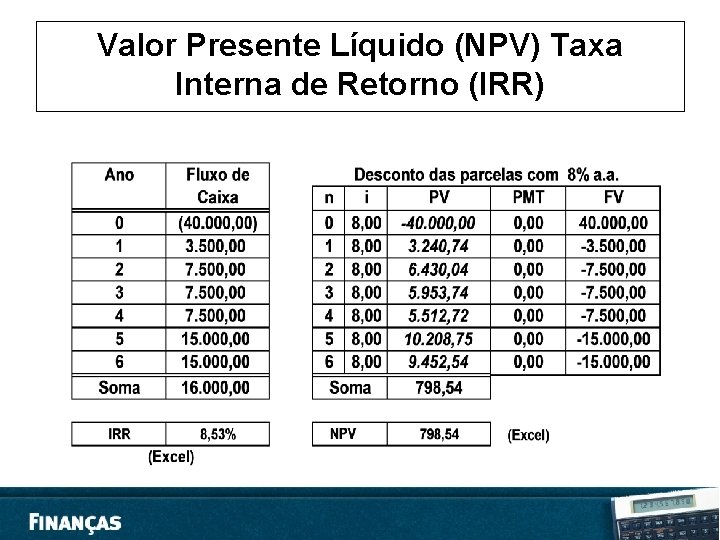
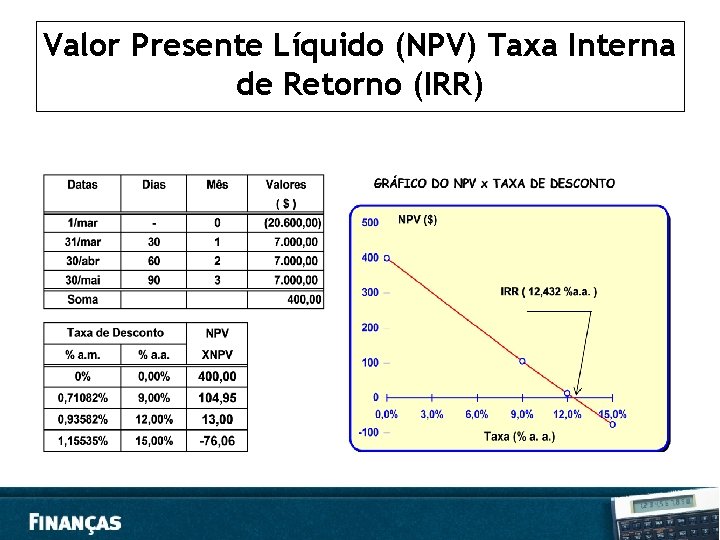
Valor presente Líquido (VPL), e Taxa Interna de Retorno (TIR) • Basicamente, toda operação financeira é representada em termos de fluxos de caixa, ou seja, em fluxos futuros esperados de recebimentos e pagamentos de caixa. A avaliação desses fluxos consiste, em essência, na comparação dos valores presentes, calculados segundo o regime de juros compostos a partir de uma dada taxa de juros, das saídas e entradas de caixa. Como consideração ao conceito do valor do dinheiro no tempo, raciocínio básico da matemática financeira, coloca-se como fundamental avaliar como adequados os métodos que considerem o fluxo de caixa descontado e que são, a saber, a Taxa Interna de Retorno (TIR) e Valor Presente Líquido (VPL).

Valor presente Líquido (VPL) • O método do Valor Presente Líquido (VPL) para análise dos fluxos de caixa é obtido pela diferença entre o valor presente dos benefícios (ou pagamentos) previstos de caixa, e o valor presente do fluxo de caixa inicial (valor do investimento, do empréstimo ou do financiamento). • Podemos inferir que o critério de decisão do método do VPL é : “ toda vez que o VPL for igual ou superior a zero, o investimento pode ser aceito ; no caso contrário, deverá ser rejeitado”.

Taxa Interna de Retorno (TIR) • A Taxa Interna de Retorno (TIR) é a taxa de juros (desconto) que iguala, em determinado momento do tempo, o valor presente das entradas (recebimentos) com o das saídas (pagamentos) previstas de caixa. • Geralmente, adota-se a data de início da operação (data zero) como a data focal de comparação dos fluxos de caixa. • Esta data representa a saída de caixa ou valor do investimento, ou empréstimo ou financiamento. O demais fluxos serão os de retorno ou recebimentos devidos.










Valor Presente Líquido (NPV) Taxa Interna de Retorno (IRR)

Valor Presente Líquido (NPV) Taxa Interna de Retorno (IRR)

Valor Presente Líquido (NPV) Taxa Interna de Retorno (IRR)

Valor Presente Líquido (NPV) Taxa Interna de Retorno (IRR)

Valor Presente Líquido (NPV) Taxa Interna de Retorno (IRR)
 Matemtica financeira
Matemtica financeira Matemtica financeira
Matemtica financeira São dadas
São dadas Programa dinheiro direto na escola
Programa dinheiro direto na escola Pdde
Pdde Lei 9613
Lei 9613 Reflexões do poeta canto viii
Reflexões do poeta canto viii Fases da lavagem de dinheiro
Fases da lavagem de dinheiro Valor absoluto y valor relativo
Valor absoluto y valor relativo Valor máximo e valor mínimo
Valor máximo e valor mínimo Valor máximo e valor mínimo
Valor máximo e valor mínimo Simplesnn
Simplesnn Jejum para vida financeira
Jejum para vida financeira Contabilidade financeira exemplos
Contabilidade financeira exemplos Amway piramide financeira
Amway piramide financeira Contabilidade comercial e financeira
Contabilidade comercial e financeira Grau de alavancagem
Grau de alavancagem Matematica financeira
Matematica financeira Holding financeira
Holding financeira Arrume tempo para ser feliz
Arrume tempo para ser feliz Perdemos muito tempo
Perdemos muito tempo Todos os nomes de polígonos
Todos os nomes de polígonos Matemtica
Matemtica Babch
Babch Propriedades dos paralelogramos 7 ano
Propriedades dos paralelogramos 7 ano Visualizamos
Visualizamos Ensino
Ensino Matemtica
Matemtica Matemtica
Matemtica Matemtica
Matemtica Parte todo
Parte todo R//s//t matematica
R//s//t matematica Valor de la amistad
Valor de la amistad Que es la onestidad
Que es la onestidad Chernar
Chernar Valor indefinido
Valor indefinido Inecuaciones lineales con valor absoluto
Inecuaciones lineales con valor absoluto Tablas de x y y
Tablas de x y y Cadena de valor de la papa
Cadena de valor de la papa Error muestral
Error muestral Cadena de valor de porter
Cadena de valor de porter Sampa valor nutricional
Sampa valor nutricional Mensaje de la familia
Mensaje de la familia Incertidumbre absoluta
Incertidumbre absoluta El valor de la obediencia
El valor de la obediencia Valor de dg
Valor de dg Desde un punto exterior p se trazan dos rectas secantes
Desde un punto exterior p se trazan dos rectas secantes Rho valor
Rho valor Halla el valor de x
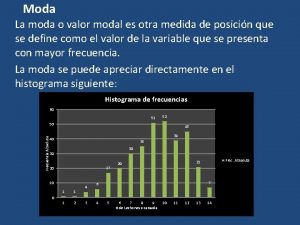
Halla el valor de x Valor de la moda
Valor de la moda Generacion de valor publico
Generacion de valor publico Valor de desecho metodo economico
Valor de desecho metodo economico Que es el valor fob
Que es el valor fob Escribe el valor del dígito subrayado
Escribe el valor del dígito subrayado Numero cuantico azimutal
Numero cuantico azimutal Valor nutricional de los cereales pdf
Valor nutricional de los cereales pdf Niveis de escrita
Niveis de escrita Ejemplos de valor absoluto
Ejemplos de valor absoluto Propiedades de una persona
Propiedades de una persona Partes del valor absoluto
Partes del valor absoluto Tfg valor de referencia
Tfg valor de referencia Valor cpan
Valor cpan Unidades del campo electrico
Unidades del campo electrico Insulina basal valores normales
Insulina basal valores normales Antimulleriana valores
Antimulleriana valores Propiedades de inecuaciones con valor absoluto
Propiedades de inecuaciones con valor absoluto El valor de una persona no se mide por
El valor de una persona no se mide por Un objeto se mueve con movimiento rectilíneo de modo tal
Un objeto se mueve con movimiento rectilíneo de modo tal Jspinner java obtener valor
Jspinner java obtener valor El valor moral de la vida humana
El valor moral de la vida humana Valor cuantitativo
Valor cuantitativo La actividad física
La actividad física Como sacar el porcentaje de interes
Como sacar el porcentaje de interes De valores
De valores Mapa de valor
Mapa de valor Un bloque que pesa 20 n se empuja sobre la cubierta
Un bloque que pesa 20 n se empuja sobre la cubierta Marketing criando valor para os clientes
Marketing criando valor para os clientes Valor
Valor Valor calorico total
Valor calorico total El silencio de negra
El silencio de negra Valor neto realizable
Valor neto realizable Probabilidad ejemplos para niños
Probabilidad ejemplos para niños Un esquema
Un esquema Vea valor economico agregado
Vea valor economico agregado Oração com valor adjetivo
Oração com valor adjetivo Dimero d elevado
Dimero d elevado Ejemplo de cuando un valor refleja un interés
Ejemplo de cuando un valor refleja un interés Valor normal de gasometria
Valor normal de gasometria Valor proteico
Valor proteico Determine o valor de bc
Determine o valor de bc Excreción
Excreción Valor de p en estadistica
Valor de p en estadistica Valor normal del anion gap
Valor normal del anion gap Ovotransferrina
Ovotransferrina Valor posicional de milesima
Valor posicional de milesima Propiedades inecuaciones valor absoluto
Propiedades inecuaciones valor absoluto Valor de t para un nivel de confianza de 90
Valor de t para un nivel de confianza de 90 Valor agonistico
Valor agonistico Q es un valor
Q es un valor Que es el margen en la cadena de valor
Que es el margen en la cadena de valor Don de piedad
Don de piedad Vectores y valores propios
Vectores y valores propios Que niega el materialismo
Que niega el materialismo Cadena de valor de porter
Cadena de valor de porter Marcas de valor
Marcas de valor Matricula duoc
Matricula duoc Que es el valor modal
Que es el valor modal Adición de números enteros
Adición de números enteros Alterna
Alterna Qu es la amistad
Qu es la amistad Valor absoluto de un numero
Valor absoluto de un numero Los determinativos
Los determinativos Inecuaciones con valor absoluto
Inecuaciones con valor absoluto Significado denotativo de zorro
Significado denotativo de zorro El saludo es un valor
El saludo es un valor Que es el valor de la responsabilidad
Que es el valor de la responsabilidad Tabla de valor posicional hasta los billones
Tabla de valor posicional hasta los billones