MATEMTICA MATEMTICA CINCIA E APLICAES Gelson Iezzi Osvaldo

MATEMÁTICA

MATEMÁTICA CIÊNCIA E APLICAÇÕES Gelson Iezzi, Osvaldo Dolce, David Degenszajn, Roberto Périgo, Nilze De Almeida – 3º ano Ensino Médio

1º Bimestre RESUMO DO BIMESTRE • • • • Neste bimestre foram trabalhados os temas: Plano cartesiano e distância entre dois pontos Ponto médio de um segmento Coordenadas do baricentro de um triângulo Condição de alinhamento de três pontos Equação geral da reta, inclinação de uma reta e coeficiente angular Equação reduzida da reta Função afim e a equação reduzida da reta Paralelismo e base média de um triângulo Forma segmentária e forma paramétrica da reta Distância entre ponto e reta e resolução gráfica da inequação do 1° grau A circunferência – equação reduzida e equação normal Posições relativas entre ponto e circunferência e reta e circunferência Intersecção de circunferências Posições relativas entre circunferências Matemática | CIÊNCIA E APLICAÇÕES | Volume 3 | 1º Bimestre

CAPÍTULO 1 – O PONTO PLANO CARTESIANO E PONTOS DO PLANO CARTESIANO O plano cartesiano Pontos do plano cartesiano P é um ponto qualquer do plano cartesiano. Traçamos por ele as retas paralelas aos eixos x e y, respectivamente. Matemática | CIÊNCIA E APLICAÇÕES | Volume 3 | 1º Bimestre

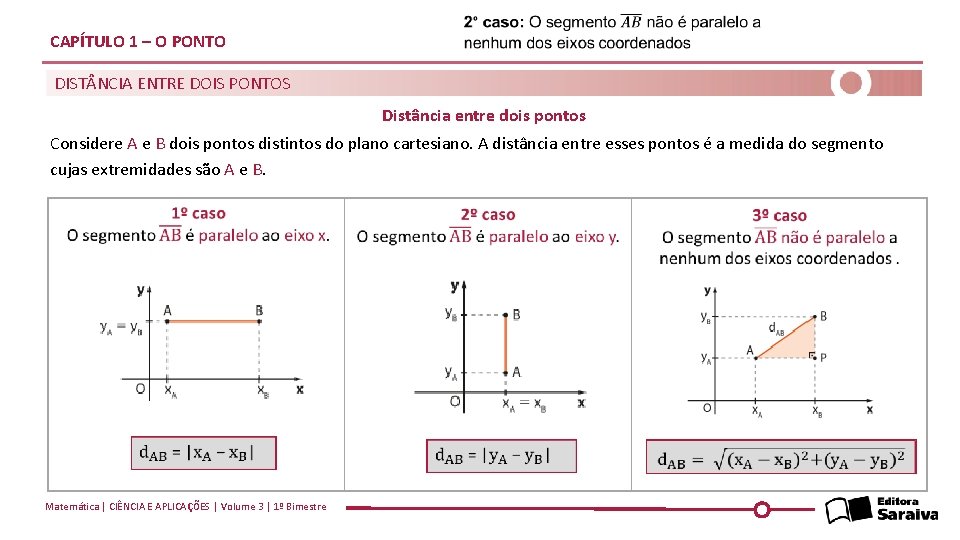
CAPÍTULO 1 – O PONTO DIST NCIA ENTRE DOIS PONTOS Distância entre dois pontos Considere A e B dois pontos distintos do plano cartesiano. A distância entre esses pontos é a medida do segmento cujas extremidades são A e B. Matemática | CIÊNCIA E APLICAÇÕES | Volume 3 | 1º Bimestre

CAPÍTULO 1 – O PONTO MÉDIO DE UM SEGMENTO E COORDENADAS DO BARICENTRO DO TRI NGULO Ponto médio de um segmento Coordenadas do baricentro de um triângulo Sendo G o baricentro do triângulo de vértices A, B e C, temos que as coordenadas de G são: Matemática | CIÊNCIA E APLICAÇÕES | Volume 3 | 1º Bimestre

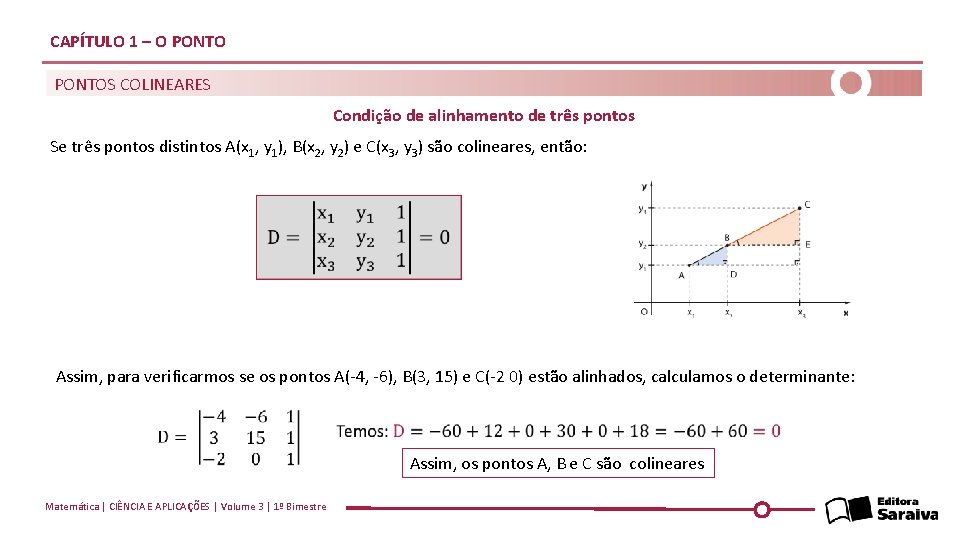
CAPÍTULO 1 – O PONTOS COLINEARES Condição de alinhamento de três pontos Se três pontos distintos A(x 1, y 1), B(x 2, y 2) e C(x 3, y 3) são colineares, então: Assim, para verificarmos se os pontos A(-4, -6), B(3, 15) e C(-2 0) estão alinhados, calculamos o determinante: Assim, os pontos A, B e C são colineares Matemática | CIÊNCIA E APLICAÇÕES | Volume 3 | 1º Bimestre

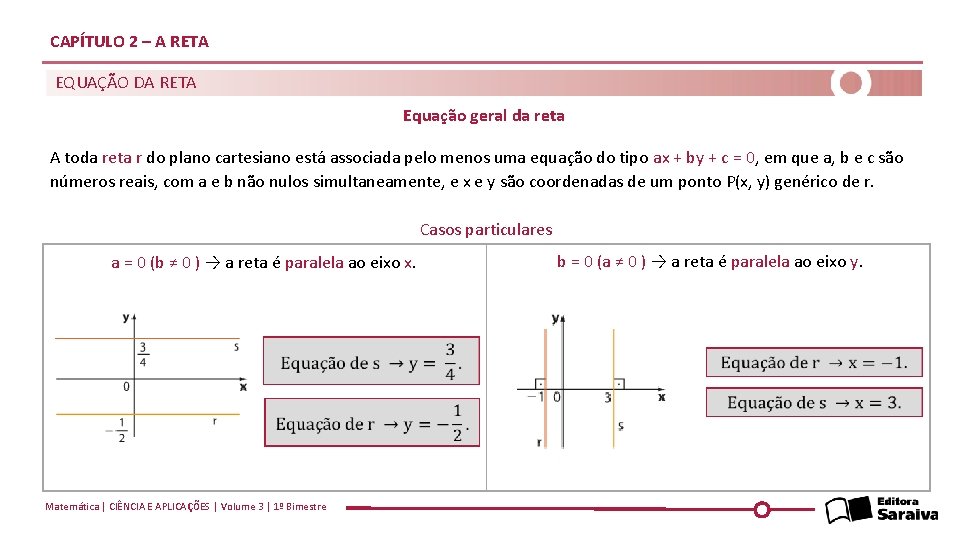
CAPÍTULO 2 – A RETA EQUAÇÃO DA RETA Equação geral da reta A toda reta r do plano cartesiano está associada pelo menos uma equação do tipo ax + by + c = 0, em que a, b e c são números reais, com a e b não nulos simultaneamente, e x e y são coordenadas de um ponto P(x, y) genérico de r. Casos particulares a = 0 (b ≠ 0 ) → a reta é paralela ao eixo x. Matemática | CIÊNCIA E APLICAÇÕES | Volume 3 | 1º Bimestre b = 0 (a ≠ 0 ) → a reta é paralela ao eixo y.

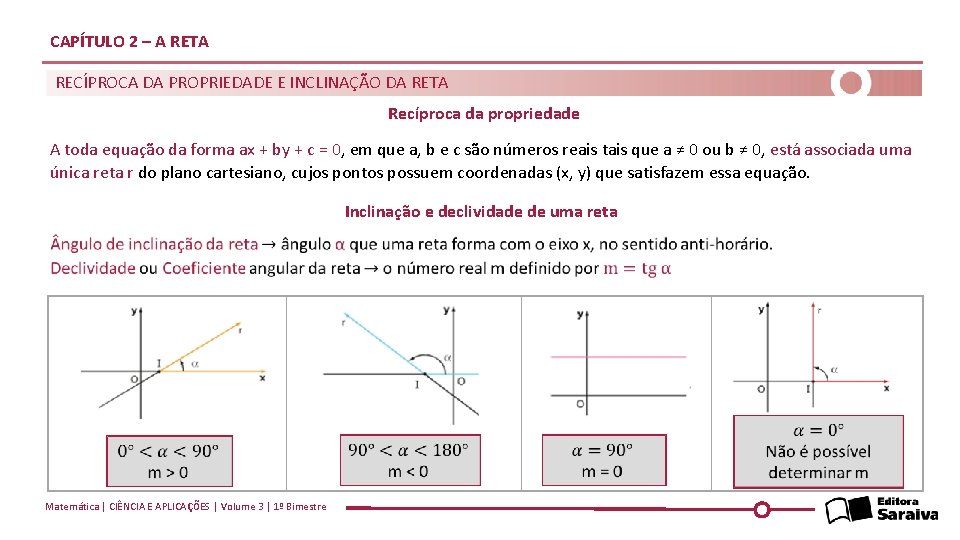
CAPÍTULO 2 – A RETA RECÍPROCA DA PROPRIEDADE E INCLINAÇÃO DA RETA Recíproca da propriedade A toda equação da forma ax + by + c = 0, em que a, b e c são números reais tais que a ≠ 0 ou b ≠ 0, está associada uma única reta r do plano cartesiano, cujos pontos possuem coordenadas (x, y) que satisfazem essa equação. Inclinação e declividade de uma reta Matemática | CIÊNCIA E APLICAÇÕES | Volume 3 | 1º Bimestre

CAPÍTULO 2 – A RETA COEFICIENTE ANGULAR E EQUAÇÃO REDUZIDA DA RETA Cálculo do coeficiente angular de uma reta a partir de dois de seus pontos ou Equação reduzida de uma reta Matemática | CIÊNCIA E APLICAÇÕES | Volume 3 | 1º Bimestre

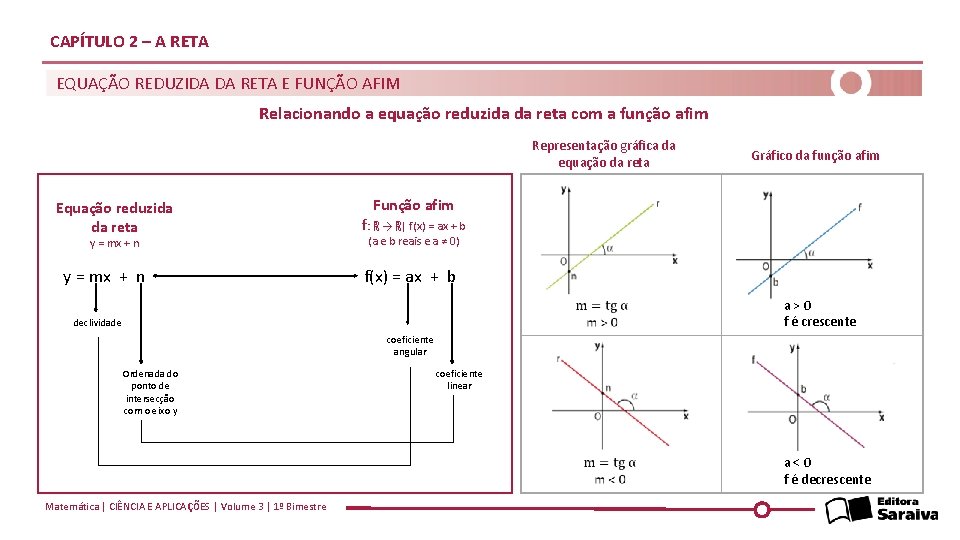
CAPÍTULO 2 – A RETA EQUAÇÃO REDUZIDA DA RETA E FUNÇÃO AFIM Relacionando a equação reduzida da reta com a função afim Representação gráfica da equação da reta Equação reduzida da reta y = mx + n Gráfico da função afim Função afim f: ℝ → ℝ| f(x) = ax + b (a e b reais e a ≠ 0) f(x) = ax + b declividade a > 0 f é crescente coeficiente angular Ordenada do ponto de intersecção com o eixo y coeficiente linear Matemática | CIÊNCIA E APLICAÇÕES | Volume 3 | 1º Bimestre a < 0 f é decrescente

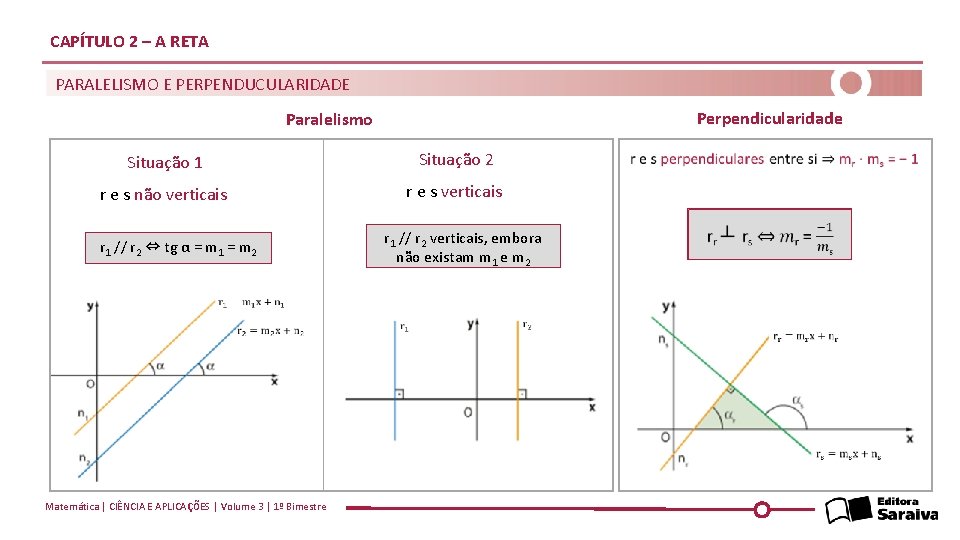
CAPÍTULO 2 – A RETA PARALELISMO E PERPENDUCULARIDADE Perpendicularidade Paralelismo Situação 1 Situação 2 r e s não verticais r e s verticais r 1 // r 2 ⇔ tg α = m 1 = m 2 r 1 // r 2 verticais, embora não existam m 1 e m 2 Matemática | CIÊNCIA E APLICAÇÕES | Volume 3 | 1º Bimestre

CAPÍTULO 2 – A RETA BASE MÉDIA DO TRI NGULO Base média de um triângulo O segmento que une os pontos médios de dois lados de um triângulo é paralelo ao terceiro lado, e sua medida é igual à metade da medida do terceiro lado. Matemática | CIÊNCIA E APLICAÇÕES | Volume 3 | 1º Bimestre

CAPÍTULO 2 – A RETA EQUAÇÕES DE UMA RETA Forma segmentária Forma paramétrica Seja r uma reta que intersecta os eixos coordenados nos pontos P(p, 0) e Q(0, q), com P e Q distintos. A forma paramétrica de uma reta estabelece a equação dessa reta expressando cada uma das coordenadas (x e y) dos pontos da reta em função de uma terceira variável, denominada parâmetro. Exemplo: Seja o par de equações de uma reta r: A equação segmentária da reta r é dada por: Assim temos: Logo: é uma equação dessa reta Matemática | CIÊNCIA E APLICAÇÕES | Volume 3 | 1º Bimestre

CAPÍTULO 2 – A RETA DIST NCIA ENTRE UM PONTO E RETA E ÁREA DO TR NGULO Distância entre um ponto e uma reta A distância d entre um ponto P(x 0, y 0) e uma reta r: ax + by + c = 0 é dada pela expressão: Área do triângulo A área A de um triângulo MNP de vértices M(x. M, y. M), N(x. N, y. N) e P(xp, yp) é dada por: Matemática | CIÊNCIA E APLICAÇÕES | Volume 3 | 1º Bimestre

CAPÍTULO 2 – A RETA INEQUAÇÕES DO 1º GRAU – RESOLUÇÃO GRÁFICA Inequação do 1º grau com duas variáveis A reta r é paralela ao eixo x A parte escurecida é a solução gráfica da inequação y ≥ 5. A parte não escurecida é solução da inequação y < 5. A reta r é paralela ao eixo y A parte escurecida é a solução gráfica da inequação x ≥ 2 A parte não escurecida é solução da inequação x < 2. Matemática | CIÊNCIA E APLICAÇÕES | Volume 3 | 1º Bimestre Método prático • Substitui a desigualdade por uma igualdade. • Traça-se a reta no plano cartesiano. • Escolhe-se um ponto genérico e verifica-se se o mesmo satisfaz ou não a desigualdade inicial. • Em caso afirmativo, a solução da inequação corresponde ao semiplano ao qual pertence o ponto genérico. • Em caso negativo, a solução da inequação corresponde ao semiplano oposto aquele ao qual pertence o ponto genérico.

CAPÍTULO 3 – A CIRCUNFERÊNCIA EQUAÇÕES DA CIRCUNFERÊNCIA Equação reduzida da circunferência Equação geral da circunferência Matemática | CIÊNCIA E APLICAÇÕES | Volume 3 | 1º Bimestre

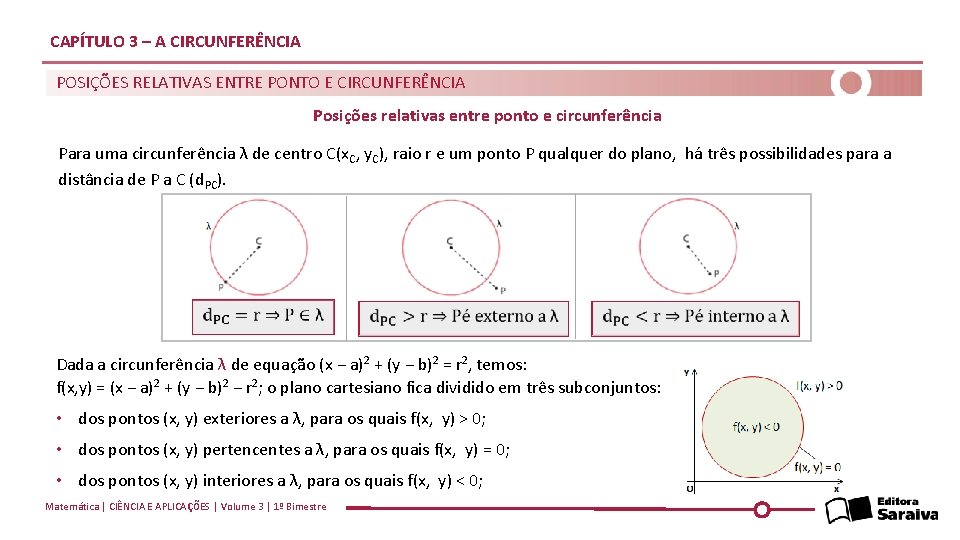
CAPÍTULO 3 – A CIRCUNFERÊNCIA POSIÇÕES RELATIVAS ENTRE PONTO E CIRCUNFERÊNCIA Posições relativas entre ponto e circunferência Para uma circunferência λ de centro C(x. C, y. C), raio r e um ponto P qualquer do plano, há três possibilidades para a distância de P a C (d. PC). Dada a circunferência λ de equação (x − a)2 + (y − b)2 = r 2, temos: f(x, y) = (x − a)2 + (y − b)2 − r 2; o plano cartesiano fica dividido em três subconjuntos: • dos pontos (x, y) exteriores a λ, para os quais f(x, y) > 0; • dos pontos (x, y) pertencentes a λ, para os quais f(x, y) = 0; • dos pontos (x, y) interiores a λ, para os quais f(x, y) < 0; Matemática | CIÊNCIA E APLICAÇÕES | Volume 3 | 1º Bimestre

CAPÍTULO 3 – A CIRCUNFERÊNCIA POSIÇÃO RELATIVA DE RETA E CIRCUNFERÊNCIA E INTERSECÇÃO DE CIRCUNFERÊNCIAS Posições relativas entre reta e circunferência Considere uma circunferência λ de centro C, e raio R e uma reta r num mesmo plano. Intersecção de circunferências Dadas duas circunferências λ 1 e λ 2, achar a intersecção de λ 1 com λ 2, é determinar os pontos P(x, y) que pertencem a ambas as curvas e que, portanto, satisfazem ao sistema formado por suas equações. Matemática | CIÊNCIA E APLICAÇÕES | Volume 3 | 1º Bimestre

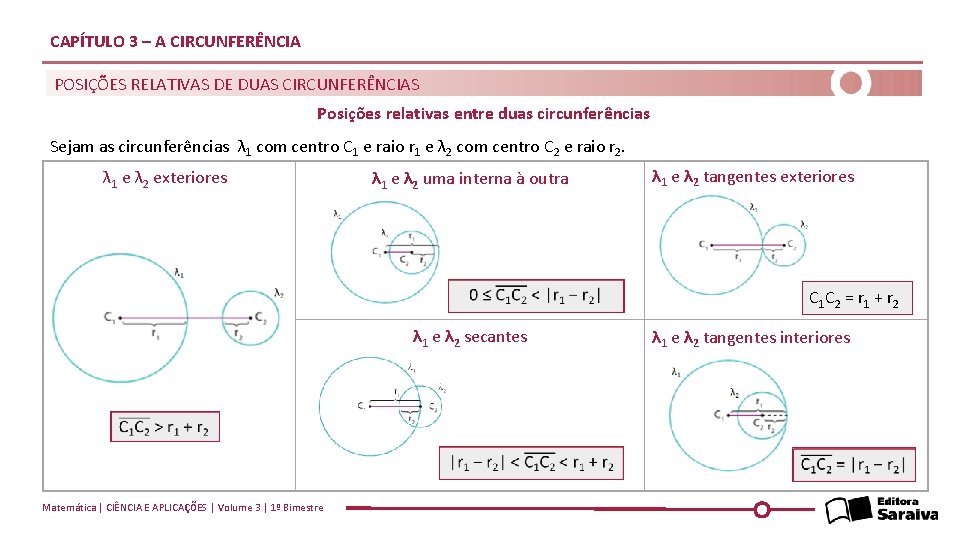
CAPÍTULO 3 – A CIRCUNFERÊNCIA POSIÇÕES RELATIVAS DE DUAS CIRCUNFERÊNCIAS Posições relativas entre duas circunferências Sejam as circunferências λ 1 com centro C 1 e raio r 1 e λ 2 com centro C 2 e raio r 2. λ 1 e λ 2 exteriores λ 1 e λ 2 uma interna à outra λ 1 e λ 2 tangentes exteriores λ 1 e λ 2 secantes C 1 C 2 = r 1 + r 2 λ 1 e λ 2 tangentes interiores Matemática | CIÊNCIA E APLICAÇÕES | Volume 3 | 1º Bimestre