MATEMTICA MATEMTICA CINCIA E APLICAES Gelson Iezzi Osvaldo

MATEMÁTICA

MATEMÁTICA CIÊNCIA E APLICAÇÕES Gelson Iezzi, Osvaldo Dolce, David Degenszajn, Roberto Périgo, Nilze De Almeida – 2º ano Ensino Médio

2º Bimestre NESTE BIMESTRE FORAM TRABALHADOS OS TEMAS: • Neste bimestre foram trabalhados os temas: • As demais voltas na circunferência trigonométrica • Função seno • Função cosseno • Matrizes – definição e representação • Matrizes especiais • Operações com matrizes: adição, subtração e multiplicação por um número real. • Multiplicação de matrizes • Matriz identidade • Matriz inversa Matemática | CIÊNCIA E APLICAÇÕES | Volume 2 | 2º Bimestre

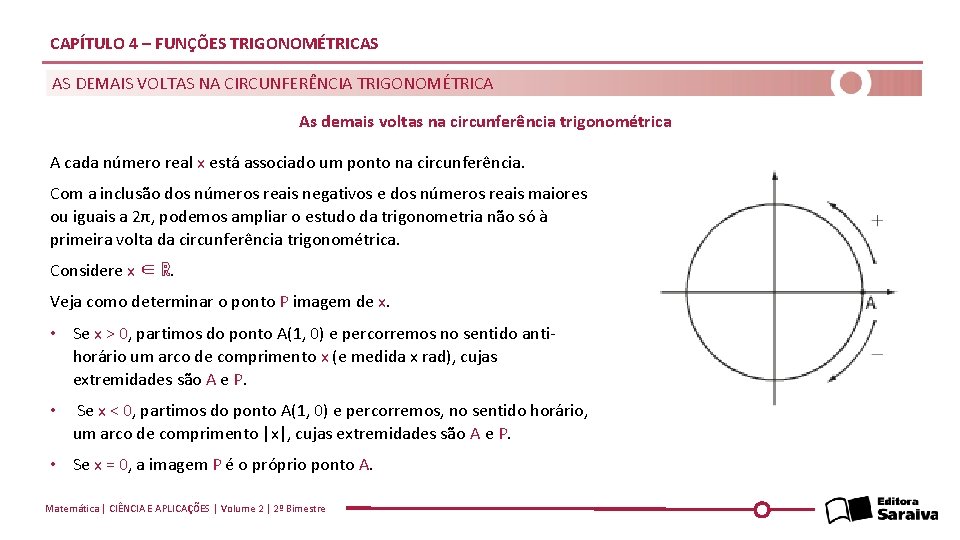
CAPÍTULO 4 – FUNÇÕES TRIGONOMÉTRICAS AS DEMAIS VOLTAS NA CIRCUNFERÊNCIA TRIGONOMÉTRICA As demais voltas na circunferência trigonométrica A cada número real x está associado um ponto na circunferência. Com a inclusão dos números reais negativos e dos números reais maiores ou iguais a 2π, podemos ampliar o estudo da trigonometria não só à primeira volta da circunferência trigonométrica. Considere x ∈ ℝ. Veja como determinar o ponto P imagem de x. • Se x > 0, partimos do ponto A(1, 0) e percorremos no sentido antihorário um arco de comprimento x (e medida x rad), cujas extremidades são A e P. • Se x < 0, partimos do ponto A(1, 0) e percorremos, no sentido horário, um arco de comprimento |x|, cujas extremidades são A e P. • Se x = 0, a imagem P é o próprio ponto A. Matemática | CIÊNCIA E APLICAÇÕES | Volume 2 | 2º Bimestre

CAPÍTULO 4 – FUNÇÕES TRIGONOMÉTRICAS AS DEMAIS VOLTAS NA CIRCUNFERÊNCIA TRIGONOMÉTRICA Arcos côngruos Um determinado ponto na circunferência trigonométrica é imagem de infinitos números reais. São também imagem de P: Matemática | CIÊNCIA E APLICAÇÕES | Volume 2 | 2º Bimestre Possuem imagem em P todos os números reais (determinam arcos côngruos)da forma:

CAPÍTULO 4 – FUNÇÕES TRIGONOMÉTRICAS FUNÇÕES PERIÓDICAS Função seno f : R → R | f(x) = sen(x) x sen x 0 0 1 D: f(x) = ℝ (domínio) 0 Im: f(x) = [− 1, 1] (imagem) - 1 0 P = 2π (período) Uma função f: A → B é periódica se existir um número real positivo p tal que f(x) = f(x + p), ∀x ∈ A. menor valor positivo de p é chamado de período de f. Matemática | CIÊNCIA E APLICAÇÕES | Volume 2 | 2º Bimestre

CAPÍTULO 4 – FUNÇÕES TRIGONOMÉTRICAS FUNÇÕES PERIÓDICAS Função cosseno x cos x 0 1 f : R → R | f(x) = cos (x) 0 - 1 0 0 D: f(x) = ℝ (domínio) Im: f(x) = [− 1, 1] (imagem) P = 2π (período) Período da função seno e da função cosseno Matemática | CIÊNCIA E APLICAÇÕES | Volume 2 | 2º Bimestre

CAPÍTULO 5 – MATRIZES DEFINIÇÃO Matrizes Sejam m e n números naturais não nulos. Uma tabela de m ⋅ n números reais dispostos em m linhas (filas horizontais) e n colunas (filas verticais) é uma matriz do tipo m x n, ou simplesmente matriz m x n. Os elementos de uma matriz são colocados entre parênteses ou entre colchetes. Matemática | CIÊNCIA E APLICAÇÕES | Volume 2 | 2º Bimestre

CAPÍTULO 5 – MATRIZES REPRESENTAÇÃO DE UMA MATRIZ Representação de uma matriz Exemplo: a 11 = − 1 a 12 = 0 a 21 = − 2 a 22 = 5 a 31 = 3 a 32 = 4 De modo geral, uma matriz A do tipo m × n é representada por A = (aij)m × n, em que i e j são números inteiros positivos tais que 1 ≤ i ≤ m, 1 ≤ j ≤ n e aij um elemento genérico de A. Matemática | CIÊNCIA E APLICAÇÕES | Volume 2 | 2º Bimestre

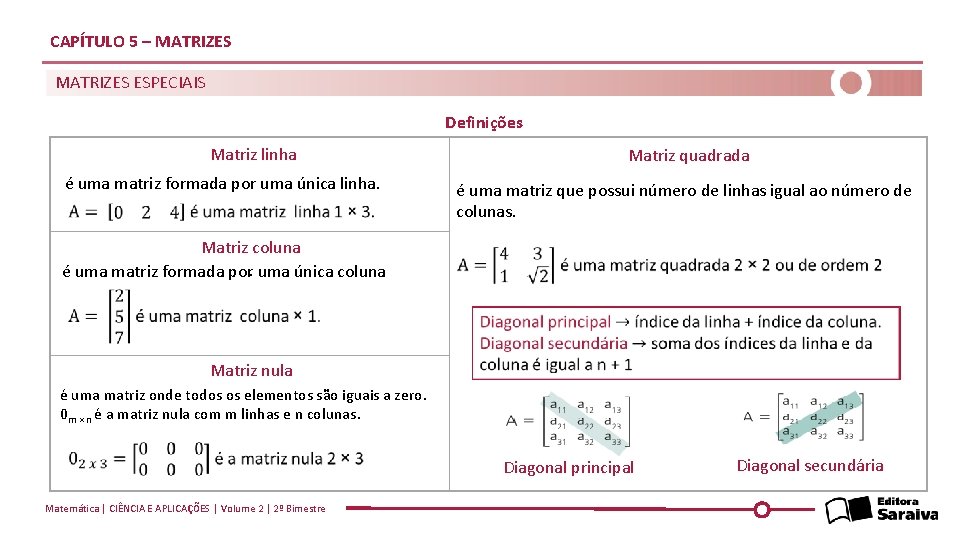
CAPÍTULO 5 – MATRIZES ESPECIAIS Definições Matriz linha é uma matriz formada por uma única linha. Matriz coluna. é uma matriz formada por uma única coluna Matriz quadrada é uma matriz que possui número de linhas igual ao número de colunas. Matriz nula é uma matriz onde todos os elementos são iguais a zero. 0 m × n é a matriz nula com m linhas e n colunas. Matemática | CIÊNCIA E APLICAÇÕES | Volume 2 | 2º Bimestre Diagonal principal Diagonal secundária

CAPÍTULO 5 – MATRIZES MATRIZ TRANSPOSTA E IGUALDADE DE MATRIZES Igualdade de matrizes Dada uma matriz A = (aij)m × n, chama-se transposta de A e indica-se por At a matriz: At = (aji)n × m Em outras palavras, a matriz At é obtida a partir de A trocando-se, ordenadamente, suas linhas pelas colunas. Igualdade de matrizes Duas matrizes A e B de mesmo tipo m × n são iguais se todos os seus elementos correspondentes são iguais. Elementos correspondentes são os que possuem mesmos índices. Matemática | CIÊNCIA E APLICAÇÕES | Volume 2 | 2º Bimestre

CAPÍTULO 5 – MATRIZES OPERAÇÕES COM MATRIZES Adição Dadas duas matrizes do mesmo tipo, A = (aij)m × n e B = (bij)m × n, a soma de A com B (representada por A + B) é a matriz C = (cij)m × n, em que cij = aij + bij, para 1 ≤ i ≤ m e 1 ≤ j ≤ n. Exemplo: Matriz oposta Seja a matriz A = (aij)m × n. Chama-se oposta de A a matriz representada por −A, tal que A + (−A) = 0 m × n, sendo 0 m × n a matriz nula do tipo m × n. Observe que a matriz −A é obtida de A trocando-se o sinal de cada um de seus elementos. Matemática | CIÊNCIA E APLICAÇÕES | Volume 2 | 2º Bimestre

CAPÍTULO 5 – MATRIZES OPERAÇÕES COM MATRIZES Adição Dadas duas matrizes do mesmo tipo A = (aij)m × n e B = (bij)m × n, chama-se diferença entre A e B (representa-se A − B) a matriz soma de A com a oposta de B, isto é: A − B = A + (−B) Multiplicação de um número real por uma matriz Seja a matriz A = (aij)m × n e k um número real. O produto de k pela matriz A (indica-se k ⋅ A) é a matriz B = (bij)m × n, em que bij = k ⋅ aij, para todo i ∈ {1, 2, …, m} e j ∈ {1, 2, …, n}. Exemplo: Matemática | CIÊNCIA E APLICAÇÕES | Volume 2 | 2º Bimestre

CAPÍTULO 5 – MATRIZES OPERAÇÕES COM MATRIZES Multiplicação de matrizes Dadas a matrizes A = (aij)m × n e B = (bij)n × p, chama-se produto de A por B, e se indica por A ⋅ B, a matriz C = (cij)m × p, em que cik = ai 1 ⋅ b 1 k + ai 2 ⋅ b 2 k + ai 3 ⋅ b 3 k + ai 4 ⋅ b 4 k + … + ain ⋅ bnk; para todo i ∈ {1, 2, …, m} e todo k ∈ {1, 2, …, p}. O procedimento para obter o elemento cik da matriz C é o que segue: 1. Tomamos ordenadamente os n elementos da linha i da matriz A: ai 1, ai 2, …, ain. (1) 2. Tomamos ordenadamente os n elementos da coluna k da matriz B: b 1 k, b 2 k, …, bnk. (2) 3. Multiplicamos o primeiro elemento de (1) pelo primeiro elemento de (2), o segundo elemento de (1) pelo segundo elemento de (2), e assim sucessivamente. 4. Somamos os produtos obtidos. Assim: Matemática | CIÊNCIA E APLICAÇÕES | Volume 2 | 2º Bimestre Garante a existência do produto

CAPÍTULO 5 – MATRIZES MULTIPLICAÇÃO DE MATRIZES Matemática | CIÊNCIA E APLICAÇÕES | Volume 2 | 2º Bimestre

CAPÍTULO 5 – MATRIZES MATRIZ IDENTIDADE Matriz identidade Seja A uma matriz quadrada de ordem n. A é denominada matriz quadrada de ordem n (indica-se por In) se os elementos de sua diagonal principal são todos iguais a 1, e os demais elementos são iguais a zero. Propriedades: Se A é quadrada de ordem n, temos: A ⋅ In = In ⋅ A = A. Se A = (aij)m × n, com m ≠ n, temos: Im ⋅ A = A e A ⋅ In = A. A multiplicação de matrizes não é comutativa, isto é, em geral, A ⋅ B ≠ B ⋅ A. Não vale a propriedade do anulamento do produto na multiplicação de matrizes. Matemática | CIÊNCIA E APLICAÇÕES | Volume 2 | 2º Bimestre

CAPÍTULO 5 – MATRIZES MATRIZ INVERSA Matriz identidade Seja A uma matriz quadrada de ordem n. A matriz A é dita inversível (ou invertível) se existe uma matriz B (quadrada de ordem n), tal que: A ⋅ B = B ⋅ A = In Lembre que In representa a matriz identidade de ordem n. Nesse caso, B é dita inversa de A e é indicada por A− 1 Matemática | CIÊNCIA E APLICAÇÕES | Volume 2 | 2º Bimestre Assim, B = A− 1

CAPÍTULO 5 – MATRIZES VERIFICAÇÃO SE UMA MATRIZ QUADRADA É OU NÃO INVERTÍVEL Do conceito de igualdades de matrizes, seguem os sistemas: É fácil verificar que a outra condição A− 1 ⋅ A, está satisfeita. Matemática | CIÊNCIA E APLICAÇÕES | Volume 2 | 2º Bimestre