Introduccin a la Informtica Terica ILI 255 ILI
































![Inducción estructural Ejemplo clásico: consideremos la siguiente definición recursiva de un árbol [conexo]. • Inducción estructural Ejemplo clásico: consideremos la siguiente definición recursiva de un árbol [conexo]. •](https://slidetodoc.com/presentation_image_h2/56ddc21a2b58dc8fb21e305a4f631bf2/image-38.jpg)









![Relaciones: equivalencia • Ejemplo: Sea S una baraja de naipe [inglés], S={ 1 , Relaciones: equivalencia • Ejemplo: Sea S una baraja de naipe [inglés], S={ 1 ,](https://slidetodoc.com/presentation_image_h2/56ddc21a2b58dc8fb21e305a4f631bf2/image-52.jpg)























- Slides: 82

Introducción a la Informática Teórica ILI 255

ILI 255 YO: Andrés Moreira amoreira@inf. utfsm. cl andres. moreira@usm. cl • “Investigador Joven” • Oficina F 130, VALPO • Horario de Consulta en Stgo: post clase del lunes

ILI 255 • Medio habitual de comunicación ILI 255 s. blogspot. com • Certámenes: 4 de mayo, 1 de junio, 13 de julio. Ayudante: Javier Robledo

ILI 255 Bibliografía: • John Hopcroft et al. , Introduction to Automata Theory, Languages and Computation [2ª ed, 2001] • Michael Sipser, Introduction to the Theory of Computation [2ª ed, 2006] • Juraj Hromkovic, Theoretical Computer Science [1ª ed, 2003] pdfs (y djvu) disponibles

ILI 255 Estarán disponibles además: • Powerpoint de las clases - Tal vez antes de la clase - Después de la clase, definitivo • Audio de las clases • Algunos links y software

ILI 255: Introducción a la Informática Teórica AKA: “TALF” Teoría de Autómatas y Lenguajes Formales

“No hay nada más práctico que una buena teoría” (K. Lewin) Teoría de Autómatas y Lenguajes Formales Máquinas (formales) Información (digital)

Preguntas “de fondo” ¿Qué es un computador? ¿Qué puede y qué no puede hacer? ¿Cuánto le cuesta hacerlo? ¿Cómo definimos formalmente un modelo de computación? ¿Cómo comparamos dos modelos distintos? ¿Cómo evaluamos la capacidad computacional de un sistema físico?

Temario 1. Strings, lenguajes, operaciones entre lenguajes 2. Lenguajes regulares, autómatas finitos 3. Expresiones regulares (“REGEXP”), aplicaciones, autómatas deterministas y no-deterministas 4. Minimización de AF 5. Gramáticas formales, jerarquía de Chomsky 6. Lenguajes de libre contexto, autómatas de pila 7. Máquinas de Turing 8. Computabilidad, complejidad computacional

Además (“bonus”) • Día lunes, en los primeros 25± 5 minutos. . . • Transparencia con fondo negro (para evitar confusiones). . .

Además (“bonus”) • Día lunes, en los primeros 25± 5 minutos. . . • Transparencia con fondo negro (para evitar confusiones). . . • Asistencia 100% voluntaria (y contenido no evaluado). Por cultura general, y contexto. Historia de “la idea de computación”

“La idea de computación” ? ? ? Algoritmos y máquinas. Se buscó entender cómo pensamos, y una vez entendido, reconstruirlo. Otra forma de decirlo: es la historia de la formalización del pensamiento abstracto. Por eso que se entrelazan dos hebras: - la que llevó a entender las bases y los límites de las matemáticas - la que llevó a los computadores y a la inteligencia artificial

Temario ahí (aproximado) -Lulio -Leibniz -Boole -Cantor -Hilbert -Gödel -Turing -. . . ? (según tiempo) • Bibliografía: Martin Davis, Engines of Logic (también disponible como pdf)

¿Qué es un algoritmo? • A la derecha, don Algoritmo, o mejor dicho, Muhammad ibn Mūsā al. Khwārizmī. • Escribió un libro en 825… …que se tradujo en el siglo XII como "Algoritmi de numero Indorum". • Eso significaba "al-Khwārizmī hablando sobre los números hindúes" …

¿Qué es un algoritmo? … pero se entendió como "Algoritmos sobre los números hindúes". • Como el libro se trataba de métodos de cálculo, se supuso que los tales "algoritmos" eran esos métodos. • Y así don "Al-Goritmo" nos hizo dos aportes: uno queriendo y el otro sin querer. Ambos importantes.

¿Qué es un algoritmo? • Es vital en matemáticas tener una buena notación (fue una virtuosa obsesión de otros personajes que vendrán luego, como Leibniz y Boole). Las matemáticas jamás podrían haber avanzado como lo hicieron, si no se hubiera reemplazado los números romanos (I, III) por los hindúes (1, 2, 3). Merci, Muhammad.

¿Qué es un algoritmo? • Pero además obtuvimos no sólo una palabra, sino un concepto clave: algoritmo. • Tener palabras precisas para conceptos no triviales, le toma siglos a las civilizaciones. Merci, traductores malos del siglo XII. • Informalmente, un algoritmo es un procedimiento claramente definido que nos permite resolver un problema en una cantidad de tiempo finita. • Formalmente: 8 siglos después.

Repaso (recordatorio) de algunas cosas Lógica. • Trabajamos con expresiones que pueden ser verdaderas o falsas (V, F), y sus valores de verdad se combinan de acuerdo a ciertas operaciones. • El resultado de las operaciones podemos representarlo mediante tablas de verdad. • También las tablas pueden servir para demostrar identidades simples. NOTA: En informática se suele usar 1 y 0 en lugar de V y F (respectivamente).

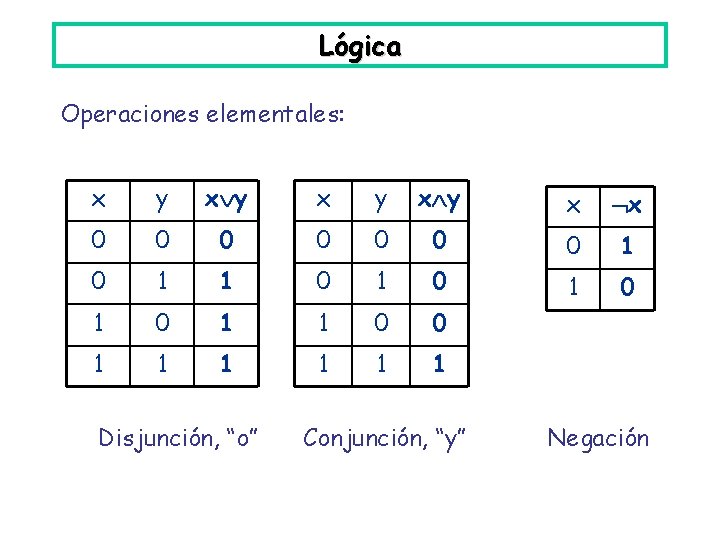
Lógica Operaciones elementales: x y x y x x 0 0 0 0 1 1 0 1 0 1 1 0 0 1 1 1 Disjunción, “o” Conjunción, “y” Negación

Lógica Algunas propiedades básicas: • Asociatividad: (x y) z = x (y z) , (x y) z = x (y z) • Distributividad: x (y z) = (x y) (x z) , x (y z) = (x y) (x z) • Leyes de Morgan: (x y) = ( x y) , (x y)= x y

Lógica Una expresión importante: P Q. La idea es que no se dé el caso en que P es cierto, pero Q es falso. Es decir, se quiere la negación de P Q. Por ley de Morgan, se quiere P Q. La equivalencia (P Q) se define mediante (P Q Q P). Uno esperaría que P Q signifique P y Q valen lo mismo. En efecto, P Q Q P P Q 0 0 1 1 1 0 0 1 0 1 1 1

Lógica A partir de una expresión de implicancia P Q aparecen otras expresiones relacionadas: • La recíproca: Q P • La contraria: P Q • La contrarrecíproca: Q P La recíproca y la contraria son equivalentes entre sí, mientras que la contrarrecíproca es equivalente a la expresión original. Por eso a veces se demuestra Q P, cuando lo que uno quiere demostrar es P Q.

Lógica Otra estrategia frecuente es la reducción al absurdo : uno supone que la conclusión es falsa, y llega a una contradicción. Es decir, suponemos que P es cierto y que Q es falso (es decir, que Q es cierto) y llegamos a algo falso: P Q = 0, que por ley de Morgan significa que P Q = 1, o sea, P Q. Notemos también que si P Q y Q R, entonces P R (ejercicio). Una consecuencia es que cuando uno quiere demostrar, por ejemplo, P Q R S, basta con demostrar P Q R S P.

Conjuntos: informalmente, una colección bien definida de objetos. “Bien definida” definición sin ambigüedad ¿“Colección”? ¿”Objetos”? No es trivial la definición exacta. Sobre todo después de la intervención de Bertrand Russell, a fines del s. XIX. En principio uno tendería a decir que toda propiedad P define un conjunto: “sean todos los x tales que P(x) es cierto”.

Conjuntos Por ejemplo, P(x)=“x es un número primo”. Entonces el conjunto R(P) será el conjunto de todos los números naturales primos. El problema aparece, por ejemplo, con P(x)=“x es un conjunto que no se incluye a si mismo”. Pregunta: ¿R(P)? Si R(P), entonces no verifica P, por lo tanto no debiera estar en R(P) Pero si R(P), entonces verifica P, y por lo tanto sí debiera estar en R(P)

Conjuntos Es la “paradoja de Russell”. ¿Por qué surge? • R(P) es un conjunto de conjuntos. Eso no es pecado; cuando uno toma (por ejemplo) “todos los subconjuntos de {0, 1, 2, 3}”, hace justamente eso. • El problema sí surge del hecho de que no hemos definido el universo de objetos que estamos considerando. Es demasiado vago!! • Solución: varias.

Conjuntos La más popular: usar los axiomas de Zermelo-Frankel para definir lo que es un conjunto (y el monstruo de la paradoja nunca aparece). Definir conjuntos a través de propiedades sí funciona, pero restringiéndose a objetos que estén en algún conjunto ya construido (como el ejemplo de los primos). Sin embargo la paradoja (o el poder) de la auto-referencia volverá a aparecer en el curso. “Los cretenses siempre mienten. ” Epiménides (un cretense)

Conjuntos • Para evitar paradojas, y tener punto de referencia, se suele trabajar dentro de un conjunto, el “universo” o “conjunto universal” U. • Se define el complemento con respecto a ese U: AC = {x U: x A} • Todo conjunto admite el subconjunto vacío, . El conjunto vacío es único. • El conjunto potencia de un conjunto A, es el conjunto P(A) formado por todos subconjuntos. • Si |A|=n, entonces |P(A)|=2 n. • Si A B, entonces P(A) P(B).

Conjuntos Inclusión de la intersección: A B Ay. A B B Inclusión en la unión: A A By. B A B Transitividad de la inclusión: (A B B C) A C Conjuntos vs Lógica: x X Y x X y Y x XY x X y Y x Xc x X

Conjuntos Conmutatividad: A B=A B y A B=B A Asociatividad: (A B) C = A (B C) y (A B) C = A (B C) Distributividad: A (B C) = (A B) (A C) y A (B C) = (A B) (A C)

Conjuntos Intersección y unión conjunto universal: A U=A y A U=U Doble complemento: (Ac)c = A Idempotencia: A A=A y A A=A De Morgan: (A B)c = Ac Bc y (A B)c = Ac Bc Absorción: A (A B) = A and A (A B) = A

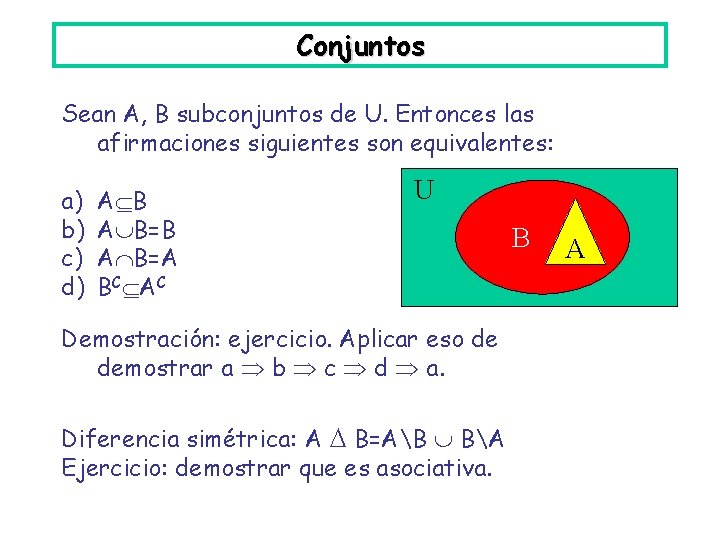
Conjuntos Sean A, B subconjuntos de U. Entonces las afirmaciones siguientes son equivalentes: a) b) c) d) A B=B A B=A BC AC U Demostración: ejercicio. Aplicar eso de demostrar a b c d a. Diferencia simétrica: A B=AB BA Ejercicio: demostrar que es asociativa. B A

Conjuntos Un par de conjuntos se dicen disjunto si su intersección es vacía (no tienen elementos en común). Nótese que AB y B son siempre disjuntos. Una colección {A 1, …Ak} se dice mutuamente disjunta si cualquier par de conjuntos de la colección es disjunto. Una colección de conjuntos no vacíos {A 1, …Ak} es una partición del conjunto A si se cumple (1) {A 1, …Ak} es mutuamente disjunta (2) A es igual a la unión de todos los Ai Si sólo se cumple lo segundo, decimos que es un recubrimiento de A.

Inducción Recordar el principio de inducción: Se usa para demostrar que una proposición P que depende de un número natural “n”, es decir, P(n), es cierta para todo “n” por sobre algún umbral n 0. Lo que se hace es demostrar: • Que P(n 0) es cierta [“caso base”] • Que si P(n) es cierta (para cualquier n ≥ n 0), entonces P(n+1) también es cierta [“paso inductivo”] En una variante, que a veces se llama inducción “fuerte”, el paso inductivo demuestra que si P(k) es cierta para todo n 0 ≤ k ≤ n, entonces lo es para n+1.

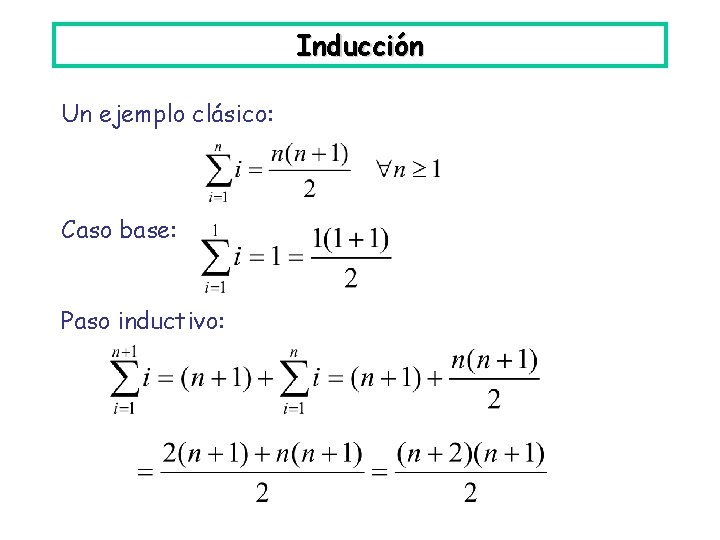
Inducción Un ejemplo clásico: Caso base: Paso inductivo:

Inducción Otros: • n 3 -n es divisible por 3, para todo n ≥ 1 • 2 x ≥ x 2, para todo x ≥ 4 • … etc (pueden mirar su cuaderno de aquellos tiempos; lo importante es que refresquen estas cosas). Un poco menos trillado: inducción “estructural”: • Generaliza la misma idea. • La usamos para demostrar propiedades de objetos definidos recursivamente.

Inducción estructural En una construcción recursiva, se tienen: • Objetos básicos (“primitivos”, “iniciales”, etc. . ) • Reglas para definir nuevos objetos a partir de un conjunto de objetos ya definidos. Entonces se demuestra que la propiedad en cuestión (el “predicado”): • Es cierta para los objetos básicos • Si es cierta para un conjunto de objetos, entonces es cierta para el nuevo objeto construido, mediante las reglas, a partir de dicho conjunto.
![Inducción estructural Ejemplo clásico consideremos la siguiente definición recursiva de un árbol conexo Inducción estructural Ejemplo clásico: consideremos la siguiente definición recursiva de un árbol [conexo]. •](https://slidetodoc.com/presentation_image_h2/56ddc21a2b58dc8fb21e305a4f631bf2/image-38.jpg)
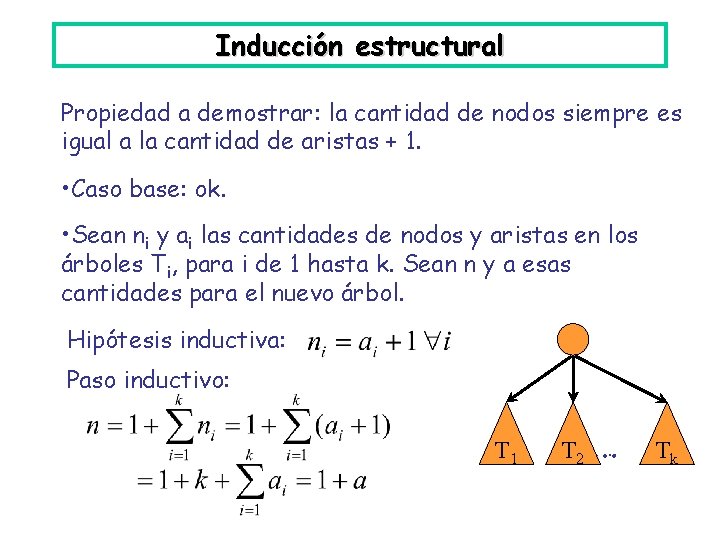
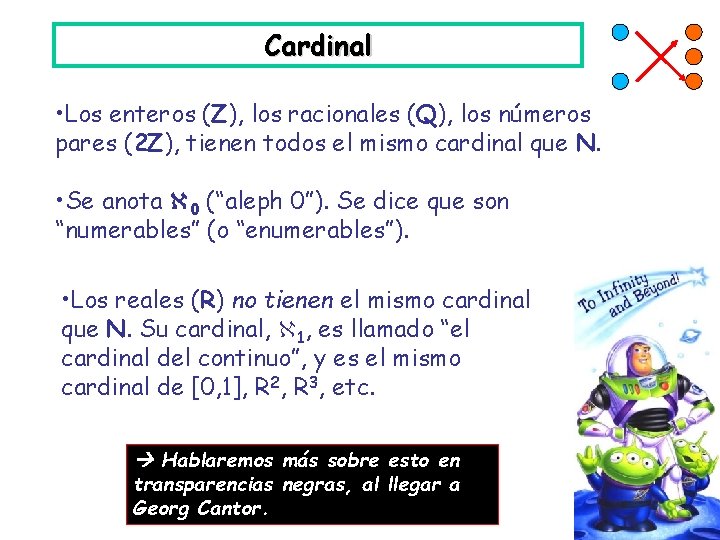
Inducción estructural Ejemplo clásico: consideremos la siguiente definición recursiva de un árbol [conexo]. • Un nodo sólo, es un árbol. • Si T 1, T 2, …, Tk son árboles disjuntos, entonces n A T 1 A T 2 también es un árbol. . A Tk

Inducción estructural Propiedad a demostrar: la cantidad de nodos siempre es igual a la cantidad de aristas + 1. • Caso base: ok. • Sean ni y ai las cantidades de nodos y aristas en los árboles Ti, para i de 1 hasta k. Sean n y a esas cantidades para el nuevo árbol. Hipótesis inductiva: n Paso inductivo: A T 1 . . . A T 2. . . A Tk

Inducción estructural Otro ejemplo típico: expresiones aritméticas. Símbolos elementales: letras, +, *, (, ) (1) Las letras son E. A. (2) Si E y F son E. A. , entonces E+F, E*F y (E) son E. A. Ejemplos: x+y, x*y+x*(z+b), ((a)), etc… Ejercicio: demostrar que en una expresión aritmética, el número de “(“ es igual al número de “)”.

Inducción estructural Números de Fibonacci: • • F(1)=F(2)=1, F(n)=F(n-1)+F(n-2) para n > 2 Demostrar que F(n) < 2 n para todo n ≥ 1 Nótese que en este caso lo podemos ver como inducción “clásica”, o bien como inducción estructural.

Tuplas y producto cartesiano • Una n-tupla ordenada es una secuencia de n elementos, escrita en la forma (x 1, …, xn). • Nótese que a diferencia de los conjuntos, donde {1, 2}={2, 1}, en una n-tupla el orden sí importa. • Por lo tanto, la única forma de que (x 1, …, xn)= (y 1, …, yn) es que x 1=y 1, …, xn=yn. • El producto cartesiano de n conjuntos A 1, . . . , An es el conjunto formado por las n-tuplas de la forma (x 1, …, xn), donde xi Ai, 1 ≤ i ≤ n :

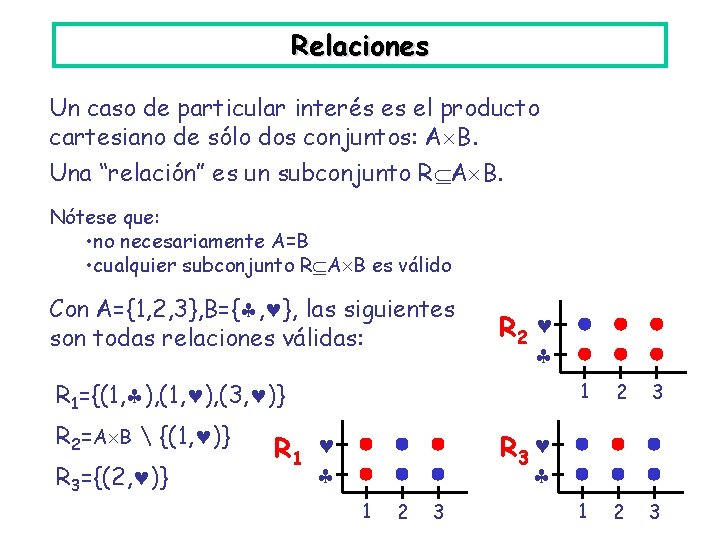
Relaciones Un caso de particular interés es el producto cartesiano de sólo dos conjuntos: A B. Una “relación” es un subconjunto R A B. Nótese que: • no necesariamente A=B • cualquier subconjunto R A B es válido Con A={1, 2, 3}, B={ , }, las siguientes son todas relaciones válidas: R 2 R 1={(1, ), (3, )} R 2=A B {(1, )} R 3={(2, )} 1 2 3 R 3 R 1 1 2 3

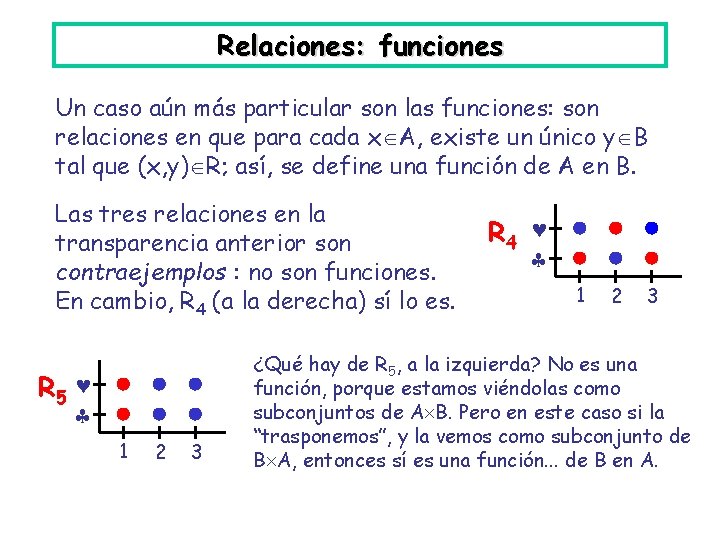
Relaciones: funciones Un caso aún más particular son las funciones: son relaciones en que para cada x A, existe un único y B tal que (x, y) R; así, se define una función de A en B. Las tres relaciones en la transparencia anterior son contraejemplos : no son funciones. En cambio, R 4 (a la derecha) sí lo es. R 5 1 2 3 R 4 1 2 3 ¿Qué hay de R 5, a la izquierda? No es una función, porque estamos viéndolas como subconjuntos de A B. Pero en este caso si la “trasponemos”, y la vemos como subconjunto de B A, entonces sí es una función. . . de B en A.

Relaciones: notación • Cuando una relación R A B es una función, y se tiene (x, y) R, solemos escribir R(x)=y. Por ejemplo, R 4(1)=. • En el caso general (en que R es una relación cualquiera), cuando (x, y) R se suele escribir x. Ry. NOTA: En lo que sigue, consideraremos relaciones dentro de un mismo conjunto: A=B, y le llamaremos “S” (o sea, A=B=S). Anotamos S 2=S S.

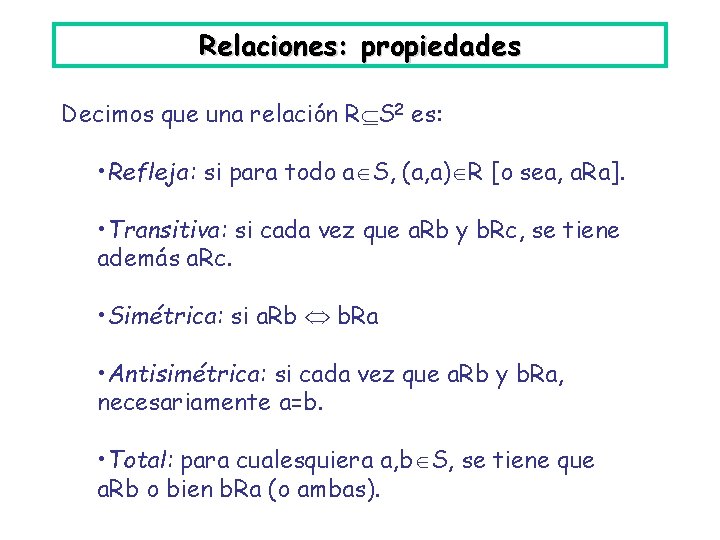
Relaciones: propiedades Decimos que una relación R S 2 es: • Refleja: si para todo a S, (a, a) R [o sea, a. Ra]. • Transitiva: si cada vez que a. Rb y b. Rc, se tiene además a. Rc. • Simétrica: si a. Rb b. Ra • Antisimétrica: si cada vez que a. Rb y b. Ra, necesariamente a=b. • Total: para cualesquiera a, b S, se tiene que a. Rb o bien b. Ra (o ambas).

Relaciones: orden Una relación de orden parcial cumple con ser refleja, transitiva y antisimétrica. • Ejemplo: Sea A un conjunto finito, S=P(A) [el conjunto potencia de A], y R definida por R = { (B, C): B, C A y B C } (es decir: es la relación de inclusión entre subconjuntos de A). NOTA: esto es lo que se llama un orden “no estricto”. En los órdenes estrictos, como “<“ y “ ”, se prohibe la igualdad, exigiendo que la relación sea antirrefleja: (a, a) R para ningún a.

Relaciones: orden Si además es total, entonces es una relación de orden total. • El ejemplo anterior es un caso de orden parcial que no es total. Para ver por qué, consideremos A={1, 2}, B={1}, C={2}. Claramente, ni B está incluído en C, ni C está incluído en B. • Consideremos S=Z (los números enteros), y la relación habitual. Ese sí es un caso de relación de orden total.

Relaciones: equivalencia Una relación de equivalencia cumple con ser refleja, transitiva y simétrica. • Ejemplo: Sean Z los números enteros, y sea m N, m 0. Definiremos la relación Rm (pues ojo, depende del m) como a Rm b a mod m = b mod m [donde a mod m es el resto de dividir a por m] Ejercicio: 1) ver que es relación de equivalencia 2) ver que a Rm b (a-b) es divisible por m.

Relaciones: equivalencia Sea R una relación de equivalencia en S. • Para cada elemento a S, definimos su clase de equivalencia [a]={ b S: a. Rb }. • El conjunto de las clases de equivalencia forma una partición de S. En efecto: • Todo elemento pertenece a alguna clase de equivalencia (la suya!). • La intersección entre dos clases de equivalencia distintas es vacía: si c [a] [b] c [a] y c [b] c. Ra y c. Rb a. Rc y c. Rb (por simetría) a. Rb (por transitividad) [a]=[b].

Relaciones: equivalencia • Ejemplo: consideremos (Z, R 3), con la relación de “igualdad módulo 3” definida antes. Entonces [0] = {. . . , -6, -3, 0, 3, 6, 9, . . . } [1] = {. . . , -5, -2, 1, 4, 7, . . . } [2] = {. . . , -4, -1, 2, 5, 8, 10, . . . } Al conjunto de clases de equivalencia (conjunto “cuociente”) lo anotamos S/R. En este caso, Z/R 3 = { [0], [1], [2] } Naturalmente, en un mismo conjunto puede definirse más de una relación de equivalencia, y cada una dará una partición distinta.
![Relaciones equivalencia Ejemplo Sea S una baraja de naipe inglés S 1 Relaciones: equivalencia • Ejemplo: Sea S una baraja de naipe [inglés], S={ 1 ,](https://slidetodoc.com/presentation_image_h2/56ddc21a2b58dc8fb21e305a4f631bf2/image-52.jpg)
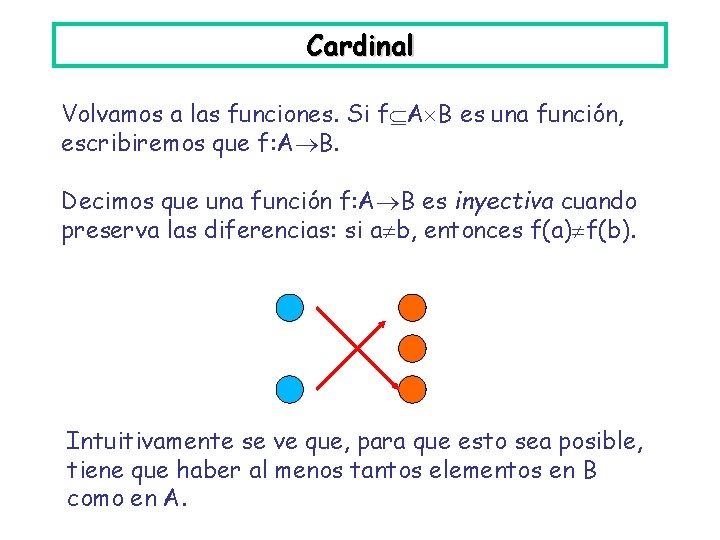
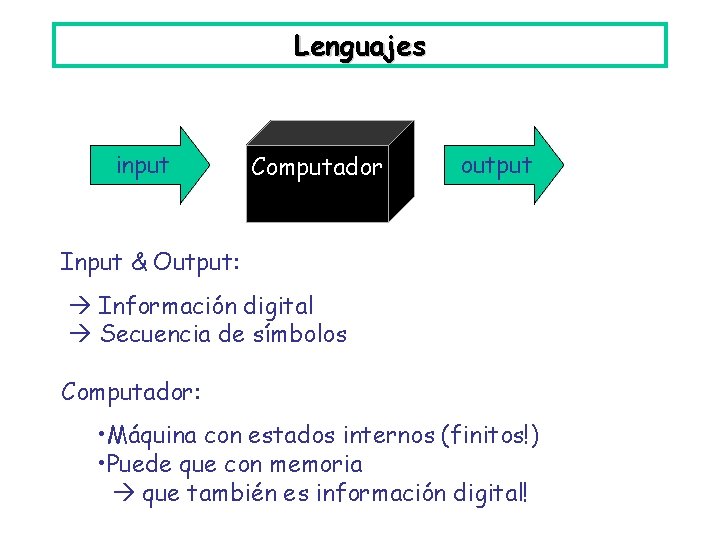
Relaciones: equivalencia • Ejemplo: Sea S una baraja de naipe [inglés], S={ 1 , 2 , . . . , K , 1 , 2 , . . . , K } y consideremos las relaciones Rp : si dos naipes son de la misma pinta Rn : si dos naipes son del mismo número Rc : si dos naipes son del mismo color R 2 : si el número de dos naipes tiene la misma paridad. ¿Cuántas clases de equivalencia distintas hay en cada caso?

Relaciones: refinamientos Nota: La relación entre relaciones de equivalencia y particiones es recíproca: dada una partición de un conjunto, podemos definir una relación de equivalencia (según si los elementos quedan juntos o no). Sean R, Q S 2 dos relaciones de equivalencia en S. Decimos que R es más fina que Q, y escribiremos R Q, si se tiene a. Rb a. Qb, a, b S Es decir, R entre elementos de S al menos tan bien como Q. Ejercicio: demostrar que si R Q, entonces las clases de equivalencia de Q son uniones de clases de equivalencia de R.

Relaciones • En el ejemplo de los naipes, Rp Rc , y Rn R 2. • Si consideramos la relación de igualdad módulo m, ¿qué deben cumplir m 1 y m 2 para que Rm 1 Rm 2 ? • Otro ejemplo: Sea otra vez A un conjunto finito cualquiera, y S=P(A) su conjunto potencia. Consideremos las relaciones R y Q dadas por: • a. Rb a=b • a. Qb |a| = |b| Entonces R Q. [Recuérdese que en este caso a y b son subconjuntos de A. |a| es el cardinal de a. ]

Relaciones Nota: en realidad siempre se tiene que la relación de identidad (“=“) es más fina que cualquier otra relación de equivalencia. Consideremos el conjunto (S) de todas las relaciones de equivalencia posibles sobre el conjunto S. Entonces “ ” es una relación en (S) !! ¿Qué tipo de relación es? Ejercicio: conteste y demuéstrelo.

Relaciones: cerradura transitiva Sea R una relación en S, no necesariamente transitiva. Definimos su cerradura transitiva como la menor relación R’ tal que R R’ y R’ es transitiva (en el peor de los casos, puede ser R’=S 2). En el caso de S finito, lo podemos ver como que “parchamos” R, agregándole los elementos que estén fallándole a la transitividad, hasta que ya no falla nada. Ejemplo: • S=ciudades del mundo • a. Rb existe un vuelo directo de a hasta b • a. R’b se puede llegar de a hasta b en avión

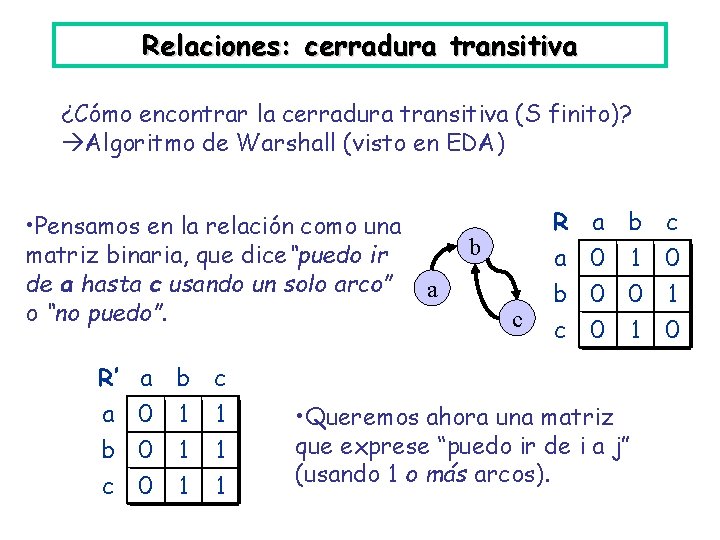
Relaciones: cerradura transitiva ¿Cómo encontrar la cerradura transitiva (S finito)? Algoritmo de Warshall (visto en EDA) • Pensamos en la relación como una matriz binaria, que dice“puedo ir de a hasta c usando un solo arco” o “no puedo”. R’ a b c 0 1 1 b a c R a b c 0 1 0 0 0 1 0 • Queremos ahora una matriz que exprese “puedo ir de i a j” (usando 1 o más arcos).

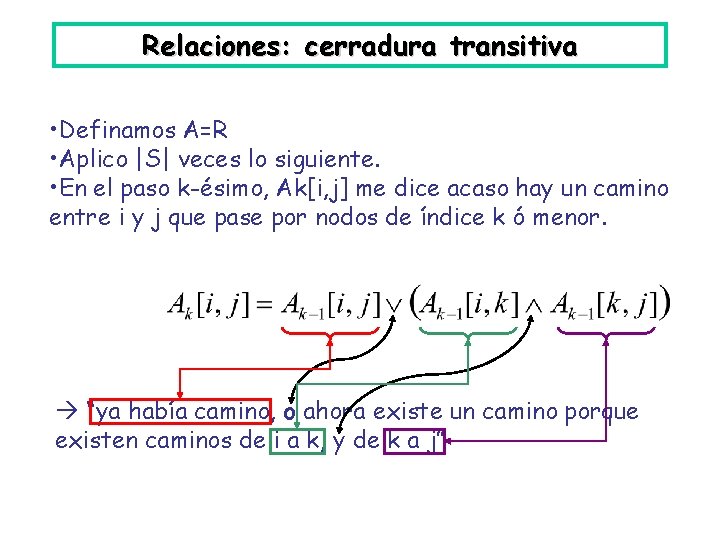
Relaciones: cerradura transitiva • Definamos A=R • Aplico |S| veces lo siguiente. • En el paso k-ésimo, Ak[i, j] me dice acaso hay un camino entre i y j que pase por nodos de índice k ó menor. “ya había camino, o ahora existe un camino porque existen caminos de i a k, y de k a j”

Relaciones: cerradura transitiva Algoritmo de Warshall: Inicialización: • A = matriz binaria representando R Iteración: • Para k=1, . . . , N Para todo i, j A[i, j] = A[i, j] (A[i, k] A[k, j]) R’ = relación representada por A [Se habla del algoritmo de Floyd-Warshall, porque esto es una variante del de Floyd para caminos más cortos en grafos. }

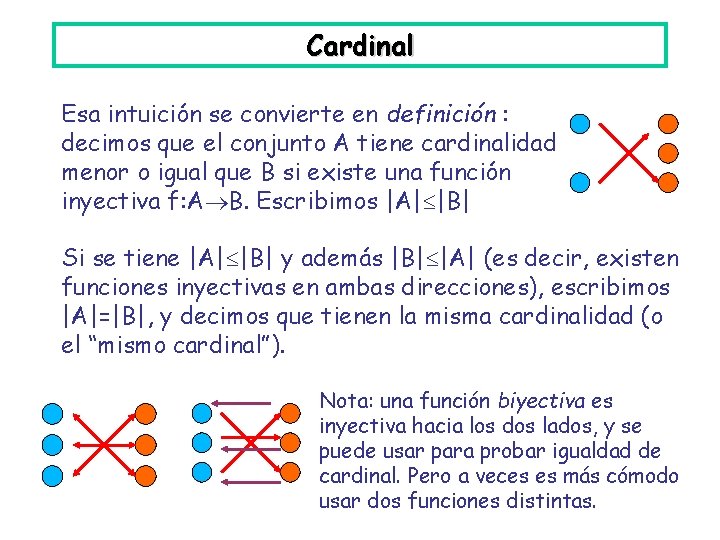
Cardinal Volvamos a las funciones. Si f A B es una función, escribiremos que f: A B. Decimos que una función f: A B es inyectiva cuando preserva las diferencias: si a b, entonces f(a) f(b). Intuitivamente se ve que, para que esto sea posible, tiene que haber al menos tantos elementos en B como en A.

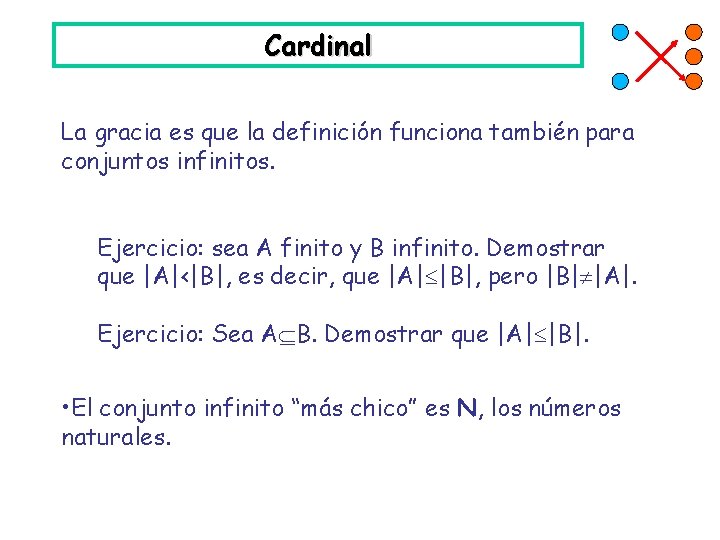
Cardinal Esa intuición se convierte en definición : decimos que el conjunto A tiene cardinalidad menor o igual que B si existe una función inyectiva f: A B. Escribimos |A| |B| Si se tiene |A| |B| y además |B| |A| (es decir, existen funciones inyectivas en ambas direcciones), escribimos |A|=|B|, y decimos que tienen la misma cardinalidad (o el “mismo cardinal”). Nota: una función biyectiva es inyectiva hacia los dos lados, y se puede usar para probar igualdad de cardinal. Pero a veces es más cómodo usar dos funciones distintas.

Cardinal Para conjuntos finitos la cardinalidad es simple: identificamos |A| con la cantidad de elementos que contiene, y |A| |B| A tiene menos elementos que B. Para el vacío, ={ }, se tiene | |=0. Un “singleton” es un conjunto de cardinal 1. Por ejemplo: {2}, { {2, 3} }, {{}}.

Cardinal La gracia es que la definición funciona también para conjuntos infinitos. Ejercicio: sea A finito y B infinito. Demostrar que |A|<|B|, es decir, que |A| |B|, pero |B| |A|. Ejercicio: Sea A B. Demostrar que |A| |B|. • El conjunto infinito “más chico” es N, los números naturales.

Cardinal • Los enteros (Z), los racionales (Q), los números pares (2 Z), tienen todos el mismo cardinal que N. • Se anota 0 (“aleph 0”). Se dice que son “numerables” (o “enumerables”). • Los reales (R) no tienen el mismo cardinal que N. Su cardinal, 1, es llamado “el cardinal del continuo”, y es el mismo cardinal de [0, 1], R 2, R 3, etc. Hablaremos más sobre esto en transparencias negras, al llegar a Georg Cantor.

Lenguajes input Computador output Input & Output: Información digital Secuencia de símbolos Computador: • Máquina con estados internos (finitos!) • Puede que con memoria que también es información digital!

Alfabetos y palabras Por lo tanto, necesitamos algunas nociones sobre cómo trabajar formalmente con secuencias de símbolos. ALFABETO: • Conjunto finito, no vacío, de símbolos. • Por lo general lo escribiremos Ejemplos: = {0, 1} = {a, b, c, . . . , z, 0, . . . , 9} = {a, . . . , z, A, . . . , Z, ” “} ese “ “ es un espacio en blanco = {(, )} los símbolos son “(“ y “)”

Alfabetos y palabras • Los símbolos son indivisibles; por lo tanto, no tendremos alfabetos del tipo { a, b, ab }. • Ya sabemos lo que es 2= . Más en general, escribiremos • Las palabras de largo k con el alfabeto serán los elementos de k. • En este caso anotaremos las tuplas sin paréntesis ni comas. Por ejemplo, si ={0, 1}, las palabras de largo 2 serán 00, 01, 10, 11.

Alfabetos y palabras • Usaremos la letra (o a veces ) para denotar la palabra vacía, formada por 0 símbolos. • Definimos 0= { } • El conjunto completo de palabras con el alfabeto se llama estrella de Kleene y corresponde a • En ocasiones se quiere excluir a la palabra vacía; en ese caso se anota

Alfabetos y palabras • Nótese que * es un conjunto infinito (pero numerable) de palabras, cada una de las cuales tiene una cantidad finita de caracteres. • Dada una palabra w *, usaremos |w| [o a veces length(w)] para denotar su longitud, es decir, la cantidad de símbolos que la componen. • Por definición, | |=0. NOTA: por lo general se usan letras minúsculas del comienzo del abecedario para denotar símbolos, mientras que las letras minúsculas del final del abecedario suelen denotar palabras.

Alfabetos y palabras • La concatenación de dos palabras se denota escribiendo una después de la otra. Por lo tanto, si u=u 1 u 2. . . un, v=v 1. . . vm, entonces w=uv será w = u 1 u 2. . . un v 1. . . vm • Dados conjuntos de palabras A y B, la concatenación de los conjuntos será AB = { w: w=uv, u A, v B } • Esto permite escribir • Nótese que, por otro lado, • Además se tiene la recursión

Alfabetos y palabras • Nótese que la concatenación es una operación asociativa : (uv)w = uvw = u(vw) • Además, tiene un elemento neutro: u = u • Algo que no verifica es conmutatividad: en general, no se cumple que uv = vu • Un conjunto no vacío dotado de una operación binaria asociativa se llama semigrupo. • Si además hay unidad (neutro), se llama monoide. • Ergo, * con la concatenación es un monoide.

Alfabetos y palabras • Una operación unaria sobre palabras es la transposición: si u=u 1 u 2. . . un, entonces su transposición es u. R = unun-1. . . u 1 Definamos de nuevo la transposición, pero de manera recursiva (con recursión sobre la longitud de la palabra): • Si |v|=0, v. R = v. • Si |v|=k>0, sean y u k-1 tales que v= u. Entonces v. R = u. R.

Alfabetos y palabras Sean u, v *. Decimos que • u es un sufijo de v x *: v=xu • u es un prefijo de v x *: v=ux • u es una subpalabra de v x, y *: v=xuy Si los x (ó y) respectivos son no nulos (o sea, distintos de ), entonces se dice que u es un sufijo (o prefijo o subpalabra) propio de v. Si u es subpalabra de v, se anota a veces o también u v.

Lenguajes Un lenguaje L sobre un alfabeto , es cualquier subconjunto de *. Ejemplo: = {a, b} * = {l, a, b, aa, ab, ba, bb, aaa, aab, aba, abb, baa, bab, bba, bbb, aaaa, … …. } L 1 = {a, aab} L 2 = {anbn: n>0} = {ab, aabb, aaabbb, …} • Ambos son lenguajes (subconjuntos de *). • L 1 es finito, mientras que L 2 es infinito. Por lo general nos interesará el caso infinito.

Lenguajes • Nótese que para cualquier alfabeto , L={ } y L= son siempre lenguajes. OJO: son distintos!! Ya que los lenguajes son simplemente conjuntos, se aplican las operaciones de conjuntos (respecto al conjunto universal *). • Intersección: L 1 L 2 = { u: u L 1 u L 2 } • Unión: L 1 L 2 = { u: u L 1 u L 2 } • Complemento: LC = * L

Lenguajes Además las siguientes operaciones se extienden de manera natural a lenguajes: • Transposición: LR = { u. R: u L } • Concatenación: L 1 L 2 = { uv: u L 1, v L 2 } • Usando eso, definimos L 0= { } Lk = L Lk-1 y con eso , Es decir, L* está formado por las concatenaciones de [cero o más] palabras de L.

Lenguajes Con frecuencia un lenguaje se define como la extensión de otro, habitualmente como la cerradura respecto a algo. Por ejemplo: dado L, podemos considerar su cerradura respecto a: • Concatenación (el menor lenguaje que incluya a L y sea cerrado bajo concatenación) Coincide con: L+

Lenguajes • Transposición (el menor lenguaje que incluya a L y sea cerrado bajo transposición) Coincide con: L LR • Subpalabras (el menor lenguaje que incluya a L y a todas las subpalabras de L) • Prefijos (el menor lenguaje que incluya a L y a todos los prefijos de palabras de L)

Lenguajes Más ejemplos de lenguajes: • ={0, . . . , 9, k, . , -}, L={w *: w es un RUT válido} • ={a, b}, L={w *: w contiene una cantidad par de “b”} • ={(, )}, L={w *: los paréntesis están bien balanceados} • ={0, 1}, L={w *: w es un nº primo} • ={0, 1}, L={w *: w= 1 a 01 b 01 c 01 n, n>2, y an+bn=cn} • =ASCII, L={w *: w es un programa en ANSI C que no se detiene nunca}

Lenguajes Como se puede ver de los ejemplos anteriores, • Un lenguaje puede representar cosas muy simples, o muy complicadas. • Suele ser interesante poder responder acaso un string pertenece o no a un lenguaje dado. • En algunos casos, es la existencia o no de strings en el lenguaje lo que interesa! Veremos en algún momento que no todo lenguaje puede ser reconocido por un computador; y en algunos casos, hay cotas mínimas para el tiempo o espacio necesarios.

Lenguajes Ejercicios: Encuentre la forma de representar: • El conjunto de los números primos, usando un alfabeto con 1 carácter. • Todos los grafos simples orientados, usando un alfabeto de a lo más 3 caracteres. • El conjunto de todas las expresiones booleanas (i. e. , fórmulas del tipo (x 1 x 2) x 3, x 1 x 2, etc).

Lenguajes Ejercicios: Sean L 1, L 2 y L 3 tres lenguajes sobre el alfabeto . 1) Demuestre que 2) 3) L 1 (L 2 L 3) = L 1 L 2 L 1 L 3 2) Demuestre que L 1 (L 2 L 3) L 1 L 2 L 1 L 3 y que esa inclusión es propia (i. e. , existen casos en que no se tiene “=“). .
 Rgb 000
Rgb 000 Terica
Terica Philippe dreyfus 1962
Philippe dreyfus 1962 Informtica
Informtica Informtica
Informtica Introduccin
Introduccin Introduccin
Introduccin Introduccin
Introduccin Induccin
Induccin Introduccin
Introduccin Introducción de las enzimas
Introducción de las enzimas Breza slavko kolar
Breza slavko kolar Char(255)
Char(255) 255-237
255-237 Hop#255
Hop#255 255 characters
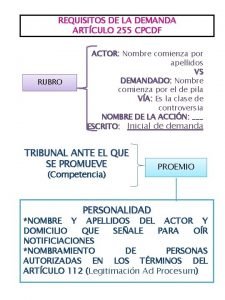
255 characters Requisitos de la demanda art 255
Requisitos de la demanda art 255 14-bit
14-bit Mp 255
Mp 255 Ak-sc 255
Ak-sc 255 Ece 255
Ece 255 Sp 255 warszawa
Sp 255 warszawa Alcatel 255
Alcatel 255 Welcome lodge 255
Welcome lodge 255 Bakara süresi 255 ayet
Bakara süresi 255 ayet Bit bajt
Bit bajt Pripovijetki ili pripovijetci
Pripovijetki ili pripovijetci Lokativ pitanje
Lokativ pitanje Oborine
Oborine Kurs za internog revizora
Kurs za internog revizora Calcane/o medical term
Calcane/o medical term Lesne zaravni u hrvatskoj karta
Lesne zaravni u hrvatskoj karta Gej
Gej Konjugacija ili sprezanje
Konjugacija ili sprezanje Glagol plakati radnja ili stanje
Glagol plakati radnja ili stanje Tombolo u hrvatskoj
Tombolo u hrvatskoj Dve tacke i zapeta u nabrajanju
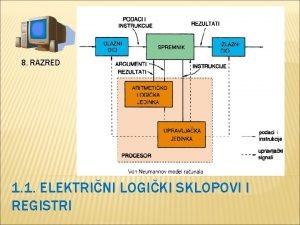
Dve tacke i zapeta u nabrajanju Elektronički logički sklopovi zadaci
Elektronički logički sklopovi zadaci Bogorodica zaštitnica
Bogorodica zaštitnica Kolibaciloza
Kolibaciloza Vrijednost ili vrjednost
Vrijednost ili vrjednost Danas je mama umrla ili možda jučer ne znam
Danas je mama umrla ili možda jučer ne znam Ili ir
Ili ir Vrednovanje ili vrjednovanje
Vrednovanje ili vrjednovanje Oboljenje ili obolenje
Oboljenje ili obolenje Gubici na robi
Gubici na robi Trijezan komparativ
Trijezan komparativ Odsjek ili odsijek
Odsjek ili odsijek Koje opasnosti mogu nastati tijekom vožnje po kiši?
Koje opasnosti mogu nastati tijekom vožnje po kiši? Pravopisni znakovi 6 razred
Pravopisni znakovi 6 razred Ponavljanje gradiva
Ponavljanje gradiva Mala i velika kazaljka
Mala i velika kazaljka Nezasitnost i bijeda vjenceslav novak
Nezasitnost i bijeda vjenceslav novak Pedagoki
Pedagoki Ponavljanje riječi u pjesmi
Ponavljanje riječi u pjesmi Riječna terasa
Riječna terasa Vrednovati ili vrjednovati
Vrednovati ili vrjednovati Otpremnica
Otpremnica Antiklinorij
Antiklinorij Slučajnost ili plan priprema
Slučajnost ili plan priprema Posljedica ili poslijedica
Posljedica ili poslijedica Bon ton ili bonton
Bon ton ili bonton Paleozoik devon
Paleozoik devon Ne pravi ili nepravi
Ne pravi ili nepravi Delikvencija ili delinkvencija
Delikvencija ili delinkvencija 7 sakramenta
7 sakramenta Bezbijednost ili bezbjednost
Bezbijednost ili bezbjednost Cilindar geometrijsko telo
Cilindar geometrijsko telo Tradicionalni roman
Tradicionalni roman Humlja
Humlja Preda mnom ili predamnom
Preda mnom ili predamnom Pakovanje ili pakiranje
Pakovanje ili pakiranje Otpremnica definicija
Otpremnica definicija Imenice primjeri
Imenice primjeri Sebe se
Sebe se Podjela zamjenica
Podjela zamjenica Kalcifert
Kalcifert Zao komparativ
Zao komparativ Svagdanji ili svagdašnji
Svagdanji ili svagdašnji Otprilike ili odprilike
Otprilike ili odprilike Diktat za 3 razred osnovne skole
Diktat za 3 razred osnovne skole Ko je pojeo jabuku adam ili eva
Ko je pojeo jabuku adam ili eva Ne znamo ili neznamo
Ne znamo ili neznamo