INFORMTICA TERICA Andrs Moreira amoreirainf utfsm cl Informtica

INFORMÁTICA TEÓRICA • Andrés Moreira amoreira@inf. utfsm. cl

Informática teórica Bibliografía: • John Hopcroft et al. , Introduction to Automata Theory, Languages and Computation [2ª ed, 2001] y 1ª ed español • Michael Sipser, Introduction to the Theory of Computation [2ª ed, 2006] pdfs disponibles

Informática Teórica AKA: “TALF” Teoría de Autómatas y Lenguajes Formales

“No hay nada más práctico que una buena teoría” (K. Lewin) Teoría de Autómatas y Lenguajes Formales Máquinas (formales) Información (digital)

Temario 0. Repaso lógica, conjuntos, relaciones 1. Strings, lenguajes, operaciones entre lenguajes 2. Lenguajes regulares, autómatas finitos 3. Expresiones regulares (“REGEXP”), aplicaciones, autómatas deterministas y no-deterministas 4. Minimización de AF 5. Gramáticas formales, jerarquía de Chomsky 6. Lenguajes de libre contexto, autómatas de pila 7. Aplicaciones

Repaso 1. Lógica 2. Conjuntos 3. Inducción 4. Relaciones 5. Clases de equivalencia 6. Refinamientos y cerradura transitiva 7. Cardinales

Repaso (recordatorio) de algunas cosas Lógica. • Expresiones verdaderas o falsas (V, F) • Sus valores de verdad se combinan de acuerdo a ciertas operaciones. • El resultado de las operaciones podemos representarlo mediante tablas de verdad. • También las tablas pueden servir para demostrar identidades simples. NOTA: En inf. se suele usar 1 y 0 en lugar de V y F

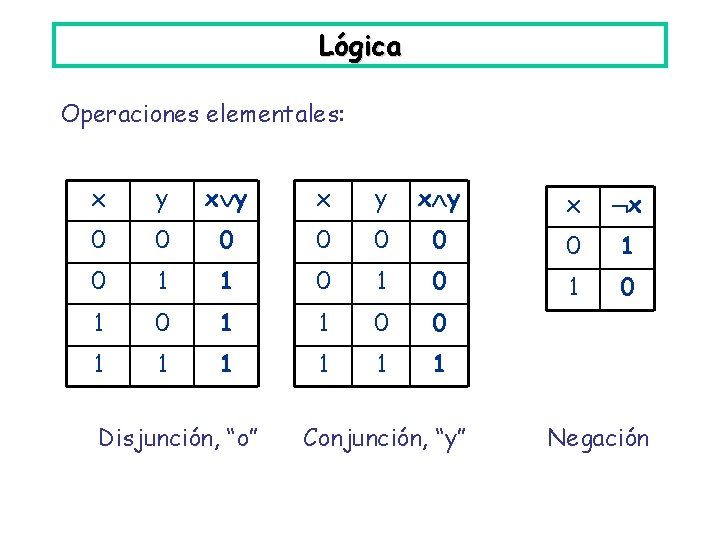
Lógica Operaciones elementales: x y x y x x 0 0 0 0 1 1 0 1 0 1 1 0 0 1 1 1 Disjunción, “o” Conjunción, “y” Negación

Lógica Algunas propiedades básicas: • Asociatividad: (x y) z = x (y z) , (x y) z = x (y z) • Distributividad: x (y z) = (x y) (x z) , x (y z) = (x y) (x z) • Leyes de Morgan: (x y) = ( x y) , (x y)= x y

Lógica Una expresión importante: P Q. La idea es que no se dé el caso en que P es cierto, pero Q es falso. Es decir, se quiere la negación de P Q. Por ley de Morgan, se quiere P Q. La equivalencia (P Q) se define mediante (P Q Q P). Uno esperaría que P Q signifique P y Q valen lo mismo. En efecto, P Q Q P P Q 0 0 1 1 1 0 0 1 0 1 1 1

Lógica A partir de una expresión de implicancia P Q aparecen otras expresiones relacionadas: • La recíproca: Q P • La contraria: P Q • La contrarrecíproca: Q P La recíproca y la contraria son equivalentes entre sí, mientras que la contrarrecíproca es equivalente a la expresión original. Por eso a veces se demuestra Q P, cuando lo que uno quiere demostrar es P Q.

Lógica Otra estrategia frecuente es la reducción al absurdo : uno supone que la conclusión es falsa, y llega a una contradicción. Es decir, suponemos que P es cierto y que Q es falso (es decir, que Q es cierto) y llegamos a algo falso: P Q = 0, que por ley de Morgan significa que P Q = 1, o sea, P Q. Notemos también que si P Q y Q R, entonces P R (ejercicio). Una consecuencia es que cuando uno quiere demostrar, por ejemplo, P Q R S, basta con demostrar P Q R S P.

Repaso 1. Lógica 2. Conjuntos 3. Inducción 4. Relaciones 5. Clases de equivalencia 6. Refinamientos y cerradura transitiva 7. Cardinales

Conjuntos: informalmente, una colección bien definida de objetos. “Bien definida” definición sin ambigüedad ¿“Colección”? ¿”Objetos”? En principio uno tendería a decir que toda propiedad P define un conjunto: “sean todos los x tales que P(x) es cierto”, o bien “sean todos los x tales que P(x) es falso”.

Conjuntos Por ejemplo, P(x)=“x es un número primo”. Entonces el conjunto R(P) será el conjunto de todos los números naturales primos. ¿Pero cuál sería el conjunto de los x que no cumplen P? • ¿Los naturales, salvo los primos? • ¿Los reales, salvo los primos? • Para tener un punto de referencia, se suele trabajar dentro de un conjunto, el “universo” o “conjunto universal” U. También evita paradojas.

Conjuntos • Se define el complemento con respecto a ese U: AC = {x U: x A} • Todo conjunto admite el subconjunto vacío, . El conjunto vacío es único. • El conjunto potencia de un conjunto A, es el conjunto P(A) formado por todos subconjuntos. • Si |A|=n, entonces |P(A)|=2 n • Si A B, entonces P(A) P(B).

Conjuntos Inclusión de la intersección: A B Ay. A B B Inclusión en la unión: A A By. B A B Transitividad de la inclusión: (A B B C) A C Conjuntos vs Lógica: x X Y x X y Y x XY x X y Y x Xc x X

Conjuntos Conmutatividad: A B=A B y A B=B A Asociatividad: (A B) C = A (B C) y (A B) C = A (B C) Distributividad: A (B C) = (A B) (A C) y A (B C) = (A B) (A C)

Conjuntos Intersección y unión conjunto universal: A U=A y A U=U Doble complemento: (Ac)c = A Idempotencia: A A=A y A A=A De Morgan: (A B)c = Ac Bc y (A B)c = Ac Bc Absorción: A (A B) = A y A (A B) = A

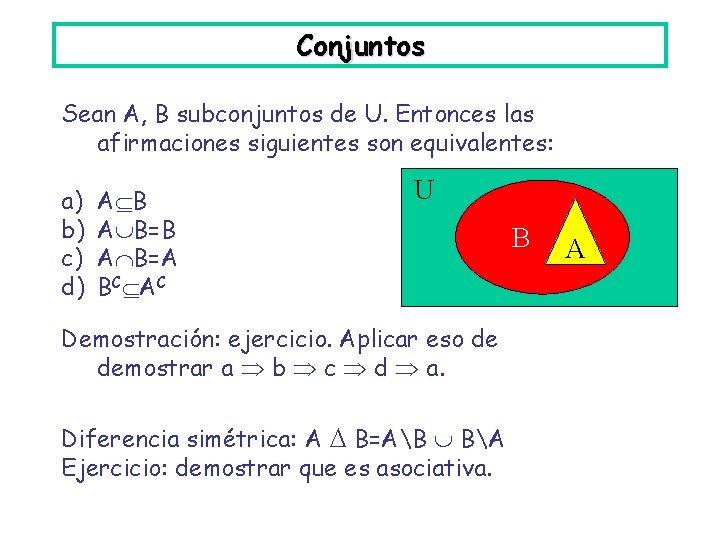
Conjuntos Sean A, B subconjuntos de U. Entonces las afirmaciones siguientes son equivalentes: a) b) c) d) A B=B A B=A BC AC U Demostración: ejercicio. Aplicar eso de demostrar a b c d a. Diferencia simétrica: A B=AB BA Ejercicio: demostrar que es asociativa. B A

Conjuntos disjuntos Un par de conjuntos se dicen disjuntos si su intersección es vacía (no tienen elementos en común). • Nótese que AB y B son siempre disjuntos. Una colección {A 1, …Ak} se dice mutuamente disjunta si cualquier par de conjuntos de la colección es disjunto.

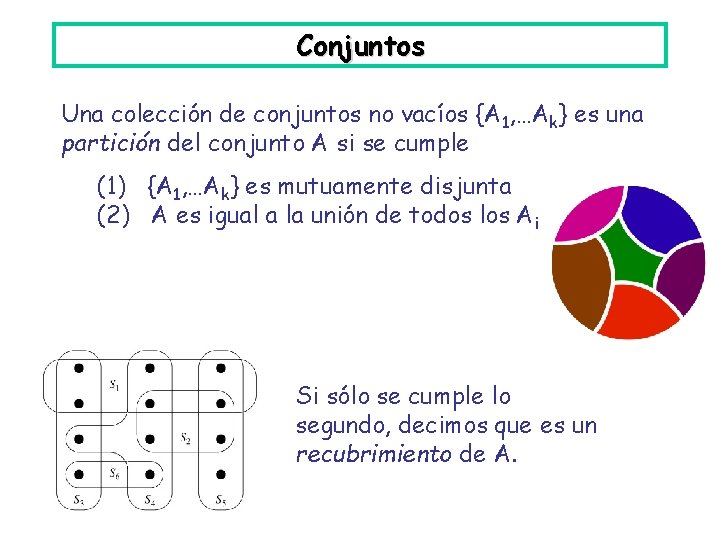
Conjuntos Una colección de conjuntos no vacíos {A 1, …Ak} es una partición del conjunto A si se cumple (1) {A 1, …Ak} es mutuamente disjunta (2) A es igual a la unión de todos los Ai Si sólo se cumple lo segundo, decimos que es un recubrimiento de A.

Repaso 1. Lógica 2. Conjuntos 3. Inducción 4. Relaciones 5. Clases de equivalencia 6. Refinamientos y cerradura transitiva 7. Cardinales

Inducción Recordar el principio de inducción: Se usa para demostrar que una proposición P que depende de un número natural “n”, es decir, P(n), es cierta para todo “n” por sobre algún umbral n 0. Lo que se hace es demostrar: • Caso base: P(n 0) es cierta • Paso inductivo: Si P(n) es cierta para n ≥ n 0, entonces P(n+1) también es cierta

Inducción Nota: En una variante, que a veces se llama inducción “fuerte”, el paso inductivo demuestra que si P(k) es cierta para todo n 0 ≤ k ≤ n, entonces lo es para n+1. Es decir, no se usa sólo el caso anterior, sino todos los anteriores.

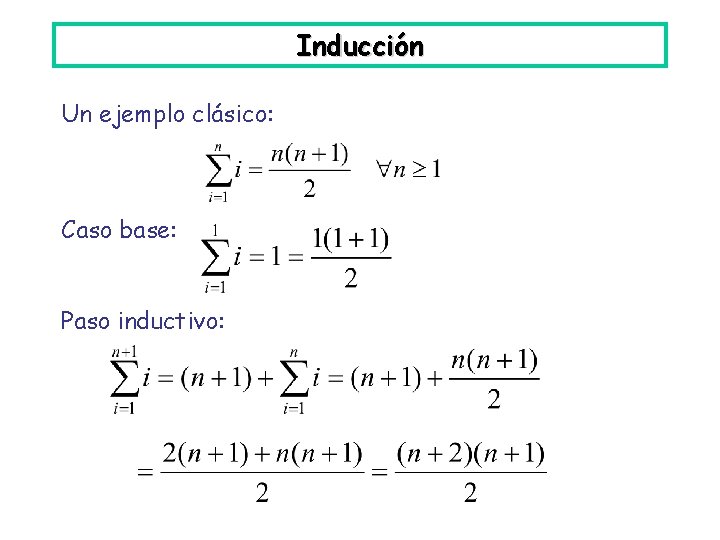
Inducción Un ejemplo clásico: Caso base: Paso inductivo:

Inducción Otros: • n 3 -n es divisible por 3, para todo n ≥ 1 • 2 x ≥ x 2, para todo x ≥ 4 • … etc (pueden mirar su cuaderno de aquellos tiempos; lo importante es que refresquen estas cosas). Un poco menos trillado: inducción “estructural”: • Generaliza la misma idea. • La usamos para demostrar propiedades de objetos definidos recursivamente.

Inducción estructural En una construcción recursiva, se tienen: • Objetos básicos (“primitivos”, “iniciales”, etc. . ) • Reglas para definir nuevos objetos a partir de un conjunto de objetos ya definidos. Entonces se demuestra que la propiedad en cuestión (el “predicado”): • Es cierta para los objetos básicos • Si es cierta para un conjunto de objetos, entonces es cierta para el nuevo objeto construido, mediante las reglas, a partir de dicho conjunto.

Inducción estructural Ejemplo clásico: consideremos la siguiente definición recursiva de un árbol [conexo]. • Un nodo sólo, es un árbol. • Si T 1, T 2, …, Tk son árboles disjuntos, entonces n A T 1 A T 2 también es un árbol. . A Tk

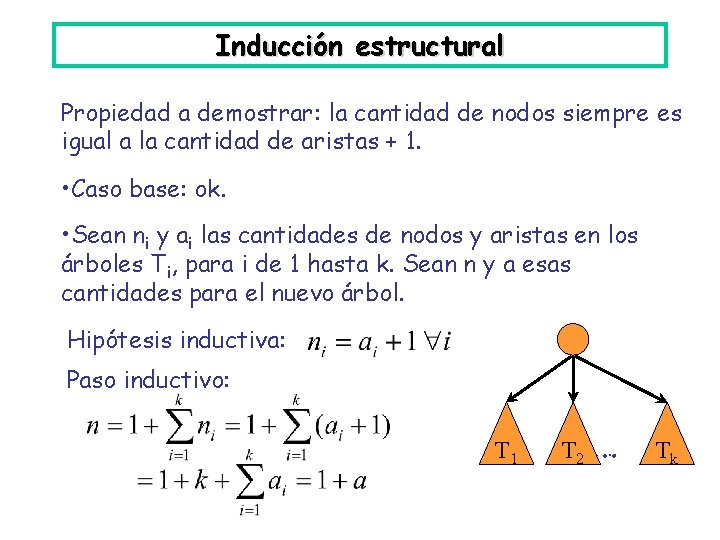
Inducción estructural Propiedad a demostrar: la cantidad de nodos siempre es igual a la cantidad de aristas + 1. • Caso base: ok. • Sean ni y ai las cantidades de nodos y aristas en los árboles Ti, para i de 1 hasta k. Sean n y a esas cantidades para el nuevo árbol. Hipótesis inductiva: n Paso inductivo: A T 1 . . . A T 2. . . A Tk

Inducción estructural Otro ejemplo típico: expresiones aritméticas. Símbolos elementales: letras, +, *, (, ) (1) Las letras son E. A. (2) Si E y F son E. A. , entonces E+F, E*F y (E) son E. A. Ejemplos: x+y, x*y+x*(z+b), ((a)), etc… Ejercicio: demostrar que en una expresión aritmética, el número de “(“ es igual al número de “)”.

Inducción estructural Números de Fibonacci: • • F(1)=F(2)=1, F(n)=F(n-1)+F(n-2) para n > 2 Demostrar que F(n) < 2 n para todo n ≥ 1 Nótese que en este caso lo podemos ver como inducción “clásica”, o bien como inducción estructural.

Repaso 1. Lógica 2. Conjuntos 3. Inducción 4. Relaciones 5. Clases de equivalencia 6. Refinamientos y cerradura transitiva 7. Cardinales

Tuplas y producto cartesiano • Una n-tupla ordenada es una secuencia de n elementos, escrita en la forma (x 1, …, xn). • Nótese que a diferencia de los conjuntos, donde {1, 2}={2, 1}, en una n-tupla el orden sí importa. • Por lo tanto, la única forma de que (x 1, …, xn)= (y 1, …, yn) es que x 1=y 1, …, xn=yn. • El producto cartesiano de n conjuntos A 1, . . . , An es el conjunto formado por las n-tuplas de la forma (x 1, …, xn), donde xi Ai, 1 ≤ i ≤ n :

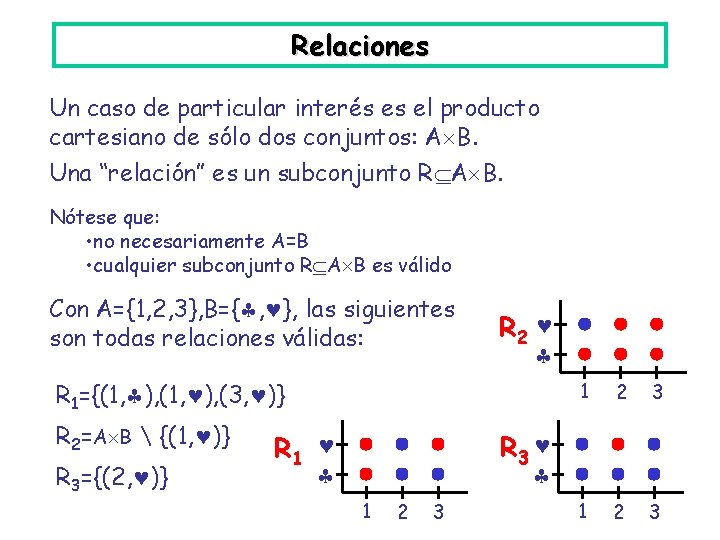
Relaciones Un caso de particular interés es el producto cartesiano de sólo dos conjuntos: A B. Una “relación” es un subconjunto R A B. Nótese que: • no necesariamente A=B • cualquier subconjunto R A B es válido Con A={1, 2, 3}, B={ , }, las siguientes son todas relaciones válidas: R 2 R 1={(1, ), (3, )} R 2=A B {(1, )} R 3={(2, )} 1 2 3 R 3 R 1 1 2 3

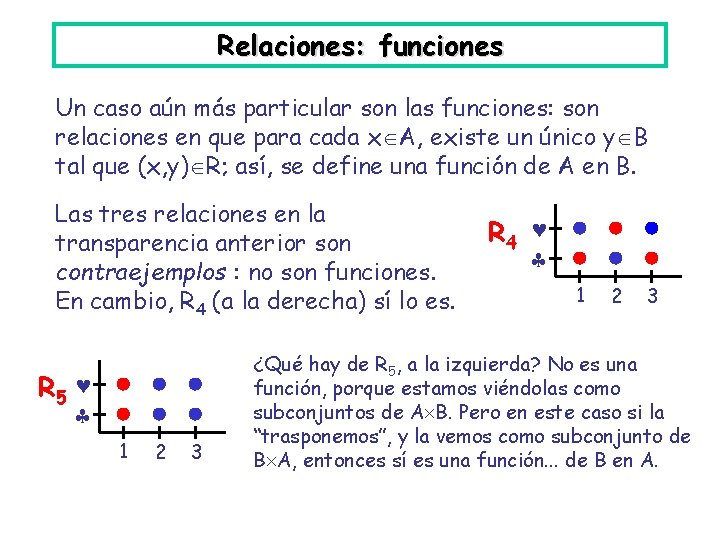
Relaciones: funciones Un caso aún más particular son las funciones: son relaciones en que para cada x A, existe un único y B tal que (x, y) R; así, se define una función de A en B. Las tres relaciones en la transparencia anterior son contraejemplos : no son funciones. En cambio, R 4 (a la derecha) sí lo es. R 5 1 2 3 R 4 1 2 3 ¿Qué hay de R 5, a la izquierda? No es una función, porque estamos viéndolas como subconjuntos de A B. Pero en este caso si la “trasponemos”, y la vemos como subconjunto de B A, entonces sí es una función. . . de B en A.

Relaciones: notación • Cuando una relación R A B es una función, y se tiene (x, y) R, solemos escribir R(x)=y. Por ejemplo, R 4(1)=. • En el caso general (en que R es una relación cualquiera), cuando (x, y) R se suele escribir x. Ry. NOTA: En lo que sigue, consideraremos relaciones dentro de un mismo conjunto: A=B, y le llamaremos “S” (o sea, A=B=S). Anotamos S 2=S S.

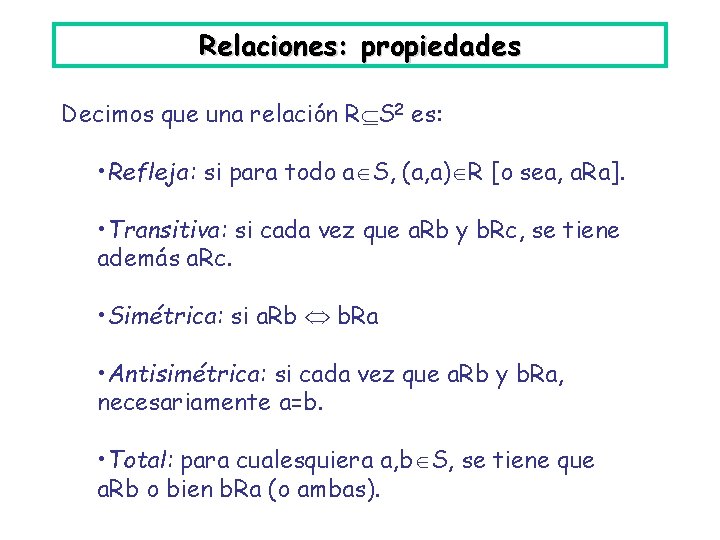
Relaciones: propiedades Decimos que una relación R S 2 es: • Refleja: si para todo a S, (a, a) R [o sea, a. Ra]. • Transitiva: si cada vez que a. Rb y b. Rc, se tiene además a. Rc. • Simétrica: si a. Rb b. Ra • Antisimétrica: si cada vez que a. Rb y b. Ra, necesariamente a=b. • Total: para cualesquiera a, b S, se tiene que a. Rb o bien b. Ra (o ambas).

Relaciones: orden Una relación de orden parcial cumple con ser refleja, transitiva y antisimétrica. • Ejemplo: Sea A un conjunto finito, S=P(A) [el conjunto potencia de A], y R definida por R = { (B, C): B, C A y B C } (es decir: es la relación de inclusión entre subconjuntos de A). NOTA: esto es lo que se llama un orden “no estricto”. En los órdenes estrictos, como “<“ y “ ”, se prohibe la igualdad, exigiendo que la relación sea antirrefleja: (a, a) R para ningún a.

Relaciones: orden Si además es total, entonces es una relación de orden total. • El ejemplo anterior es un caso de orden parcial que no es total. Para ver por qué, consideremos A={1, 2}, B={1}, C={2}. Claramente, ni B está incluído en C, ni C está incluído en B. • Consideremos S=Z (los números enteros), y la relación habitual. Ese sí es un caso de relación de orden total.

Repaso 1. Lógica 2. Conjuntos 3. Inducción 4. Relaciones 5. Clases de equivalencia 6. Refinamientos y cerradura transitiva 7. Cardinales

Relaciones: equivalencia Una relación de equivalencia cumple con ser refleja, transitiva y simétrica. • Ejemplo: Sean Z los números enteros, y sea m N, m 0. Definiremos la relación Rm (pues ojo, depende del m) como a Rm b a mod m = b mod m [donde a mod m es el resto de dividir a por m] Ejercicio: 1) ver que es relación de equivalencia 2) ver que a Rm b (a-b) es divisible por m.

Relaciones: equivalencia Sea R una relación de equivalencia en S. • Para cada elemento a S, definimos su clase de equivalencia [a]={ b S: a. Rb }. • El conjunto de las clases de equivalencia forma una partición de S. En efecto: • Todo elemento pertenece a alguna clase de equivalencia (la suya!). • La intersección entre dos clases de equivalencia distintas es vacía: si c [a] [b] c [a] y c [b] c. Ra y c. Rb a. Rc y c. Rb (por simetría) a. Rb (por transitividad) [a]=[b].

Relaciones: equivalencia • Ejemplo: consideremos (Z, R 3), con la relación de “igualdad módulo 3” definida antes. Entonces [0] = {. . . , -6, -3, 0, 3, 6, 9, . . . } [1] = {. . . , -5, -2, 1, 4, 7, . . . } [2] = {. . . , -4, -1, 2, 5, 8, 10, . . . } Al conjunto de clases de equivalencia (conjunto “cuociente”) lo anotamos S/R. En este caso, Z/R 3 = { [0], [1], [2] } Naturalmente, en un mismo conjunto puede definirse más de una relación de equivalencia, y cada una dará una partición distinta.

Relaciones: equivalencia • Ejemplo: Sea S una baraja de naipe [inglés], S={ 1 , 2 , . . . , K , 1 , 2 , . . . , K } y consideremos las relaciones Rp : si dos naipes son de la misma pinta Rn : si dos naipes son del mismo número Rc : si dos naipes son del mismo color R 2 : si el número de dos naipes tiene la misma paridad. ¿Cuántas clases de equivalencia distintas hay en cada caso?

Relaciones: equivalencia Nota: La relación entre relaciones de equivalencia y particiones es recíproca: dada una partición de un conjunto, siempre podemos definir una relación de equivalencia (según si los elementos quedan juntos o no) cuyas clases de equivalencias correspondan a esa partición.

Repaso 1. Lógica 2. Conjuntos 3. Inducción 4. Relaciones 5. Clases de equivalencia 6. Refinamientos y cerradura transitiva 7. Cardinales

Relaciones: refinamientos Sean R, Q S 2 dos relaciones de equivalencia en S. Decimos que R es más fina que Q, y escribiremos R Q, si se tiene a. Rb a. Qb, a, b S Es decir, R distingue entre elementos de S al menos tan bien como Q. Ejercicio: demostrar que si R Q, entonces las clases de equivalencia de Q son uniones de clases de equivalencia de R.

Relaciones • En el ejemplo de los naipes, Rp Rc , y Rn R 2. • Si consideramos la relación de igualdad módulo m, ¿qué deben cumplir m 1 y m 2 para que Rm 1 Rm 2 ? • Otro ejemplo: Sea otra vez A un conjunto finito cualquiera, y S=P(A) su conjunto potencia. Consideremos las relaciones R y Q dadas por: • a. Rb a=b • a. Qb |a| = |b| Entonces R Q. [Recuérdese que en este caso a y b son subconjuntos de A. |a| es el cardinal de a. ]

Relaciones Nota: en realidad siempre se tiene que la relación de identidad (“=“) es más fina que cualquier otra relación de equivalencia. Consideremos el conjunto (S) de todas las relaciones de equivalencia posibles sobre el conjunto S. Entonces “ ” es una relación en (S) !! ¿Qué tipo de relación es? Ejercicio: conteste y demuéstrelo.

Relaciones: cerradura transitiva Sea R una relación en S, no necesariamente transitiva. Definimos su cerradura transitiva como la menor relación R’ tal que R R’ y R’ es transitiva (en el peor de los casos, puede ser R’=S 2). En el caso de S finito, lo podemos ver como que “parchamos” R, agregándole los elementos que estén fallándole a la transitividad, hasta que ya no falla nada. Ejemplo: • S=ciudades del mundo • a. Rb existe un vuelo directo de a hasta b • a. R’b se puede llegar de a hasta b en avión

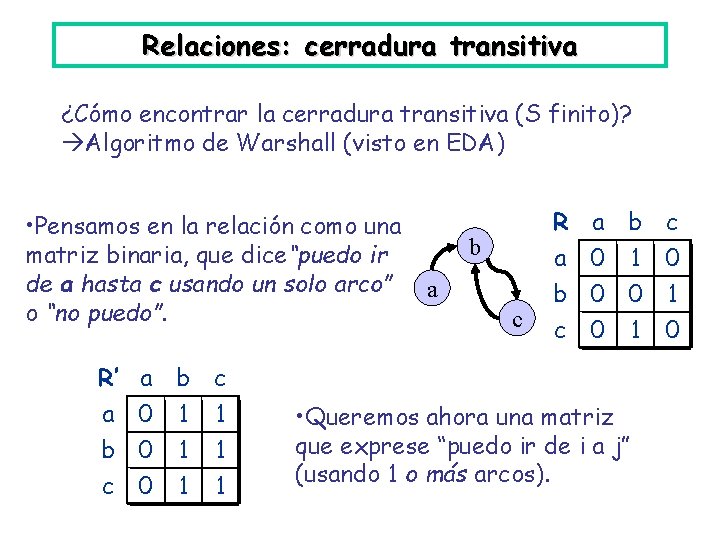
Relaciones: cerradura transitiva ¿Cómo encontrar la cerradura transitiva (S finito)? Algoritmo de Warshall (visto en EDA) • Pensamos en la relación como una matriz binaria, que dice“puedo ir de a hasta c usando un solo arco” o “no puedo”. R’ a b c 0 1 1 b a c R a b c 0 1 0 0 0 1 0 • Queremos ahora una matriz que exprese “puedo ir de i a j” (usando 1 o más arcos).

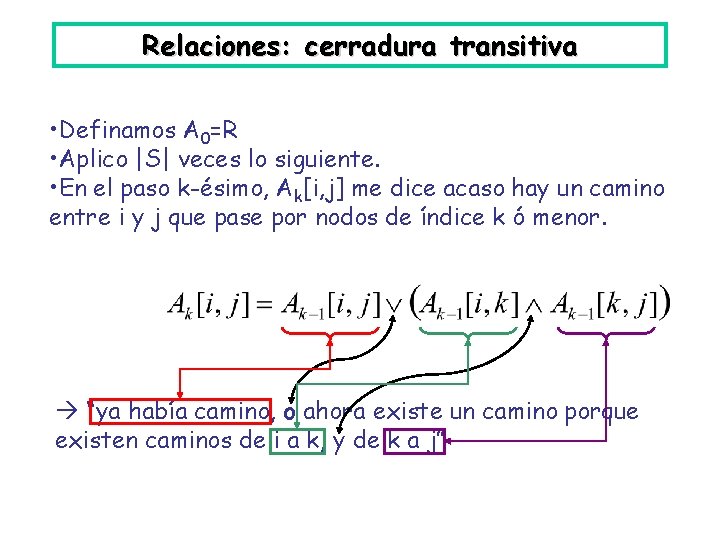
Relaciones: cerradura transitiva • Definamos A 0=R • Aplico |S| veces lo siguiente. • En el paso k-ésimo, Ak[i, j] me dice acaso hay un camino entre i y j que pase por nodos de índice k ó menor. “ya había camino, o ahora existe un camino porque existen caminos de i a k, y de k a j”

Relaciones: cerradura transitiva Algoritmo de Warshall: Inicialización: • A = matriz binaria representando R Iteración: • Para k=1, . . . , N Para todo i, j A[i, j] = A[i, j] (A[i, k] A[k, j]) R’ = relación representada por A [Se habla del algoritmo de Floyd-Warshall, porque esto es una variante del de Floyd para caminos más cortos en grafos. }

Repaso 1. Lógica 2. Conjuntos 3. Inducción 4. Relaciones 5. Clases de equivalencia 6. Refinamientos y cerradura transitiva 7. Cardinales

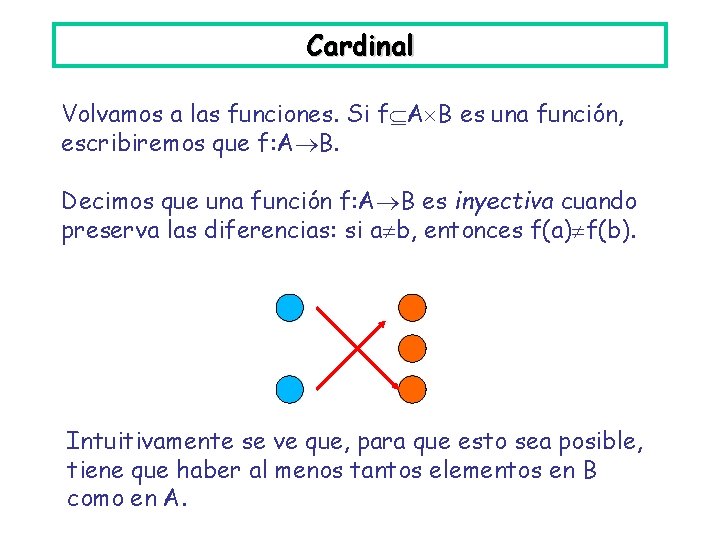
Cardinal Volvamos a las funciones. Si f A B es una función, escribiremos que f: A B. Decimos que una función f: A B es inyectiva cuando preserva las diferencias: si a b, entonces f(a) f(b). Intuitivamente se ve que, para que esto sea posible, tiene que haber al menos tantos elementos en B como en A.

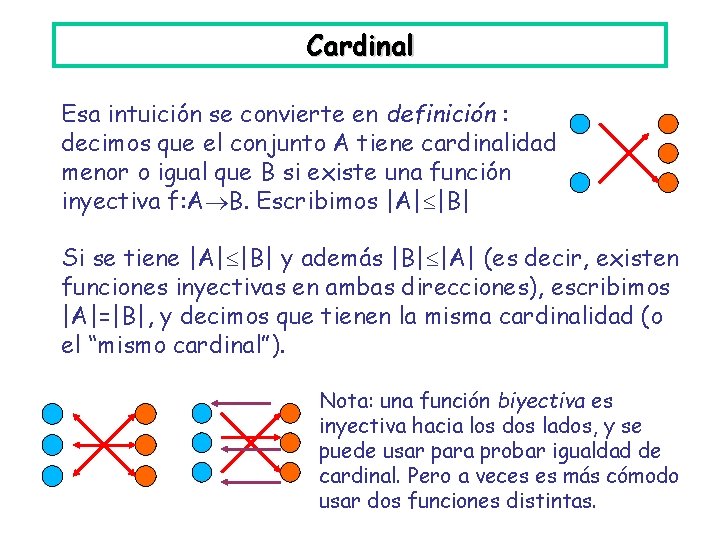
Cardinal Esa intuición se convierte en definición : decimos que el conjunto A tiene cardinalidad menor o igual que B si existe una función inyectiva f: A B. Escribimos |A| |B| Si se tiene |A| |B| y además |B| |A| (es decir, existen funciones inyectivas en ambas direcciones), escribimos |A|=|B|, y decimos que tienen la misma cardinalidad (o el “mismo cardinal”). Nota: una función biyectiva es inyectiva hacia los dos lados, y se puede usar para probar igualdad de cardinal. Pero a veces es más cómodo usar dos funciones distintas.

Cardinal Para conjuntos finitos la cardinalidad es simple: identificamos |A| con la cantidad de elementos que contiene, y |A| |B| A tiene menos elementos que B. Para el vacío, ={ }, se tiene | |=0. Un “singleton” es un conjunto de cardinal 1. Por ejemplo: {2}, { {2, 3} }, {{ }}.

Cardinal La gracia es que la definición funciona también para conjuntos infinitos. Ejercicio: sea A finito y B infinito. Demostrar que |A|<|B|, es decir, que |A| |B|, pero |B| |A|. Ejercicio: Sea A B. Demostrar que |A| |B|. • El conjunto infinito “más chico” es N, los números naturales.

Cardinal • Los enteros (Z), los racionales (Q), los números pares (2 Z), tienen todos el mismo cardinal que N. • Se anota 0 (“aleph 0”). Se dice que son “contables”. • Los reales (R) no tienen el mismo cardinal que N. Su cardinal, 1, es llamado “el cardinal del continuo”, y es el mismo cardinal de [0, 1], R 2, R 3, etc.

Fin del repaso