Graph theory a graph is a finite set














































































- Slides: 129

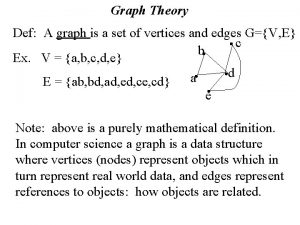
Graph theory a graph is a finite set of dots called vertices (or nodes) connected by links called edges (or arcs). a simple graph is set of vertices V and set of unordered pairs of distinct elements of V called edges. Not all graphs are simple. Sometimes a pair of vertices are connected by multiple edge called parallel edges yielding a multigraph. At times vertices are even connected to themselves by an edge called a loop. Finally, edges can also be given a direction yielding a directed graph (or digraph). a multigraph is a graph with multiple edges between the same vertices. Formally: a multigraph is a set V of vertices along, a set E of edges, and a function f from E to {{u, v}|u, v in V; u, v distinct}. An edge is said to be incident on its endpoints or vertices. Two vertices are adjacent if they are connected by an edge. Two edges incident on the same vertex are called adjacent. A vertex with a loop is adjacent to itself. A vertex on which no edges are incident is called isolated. kavita hatwal math 231 fall 2002

Example: Graph • Let G = (V, E) where – V = {A, B, C, D, E}, – E = {{A, B}, {A, C}, {B, B}, {B, C}, {D, E}}. A B E C D kavita hatwal math 231 fall 2002

Terminology • The edge {a, b} has endpoints a and b. • The edge {a, b} connects the endpoints a and b. • Vertices that are connected by an edge are adjacent. kavita hatwal math 231 fall 2002

Directed Graphs • A directed graph G is a pair (V, E) where – V is a set of vertices, – E is a multiset of ordered pairs of vertices. • That is, each edge has a direction. • A directed graph is also called a digraph. kavita hatwal math 231 fall 2002

Example: Directed Graph n Let G = (V, E) where n n V = {A, B, C, D, E}, E = {(A, B), (A, C), (C, A), (B, B), (B, C), E)). A B E C D kavita hatwal math 231 fall 2002 (D,

Simple Graphs • A simple graph G is a pair (V, E) where – V is a set of vertices, – E is a set of edges, where each edge is a set of vertices. kavita hatwal math 231 fall 2002

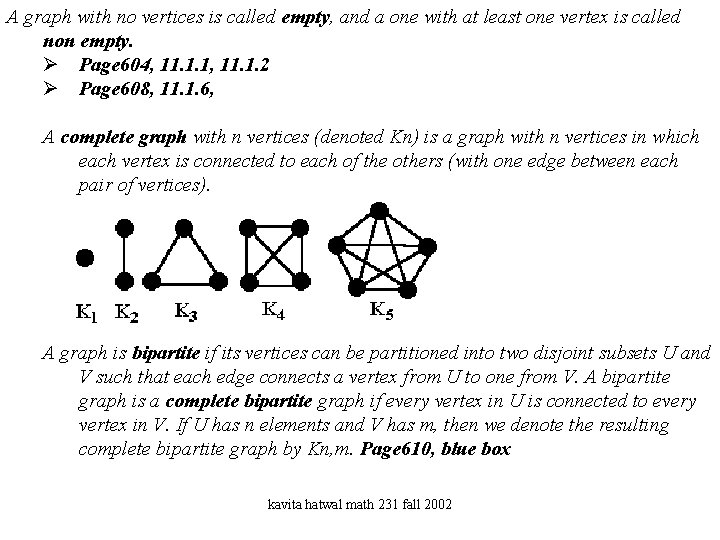
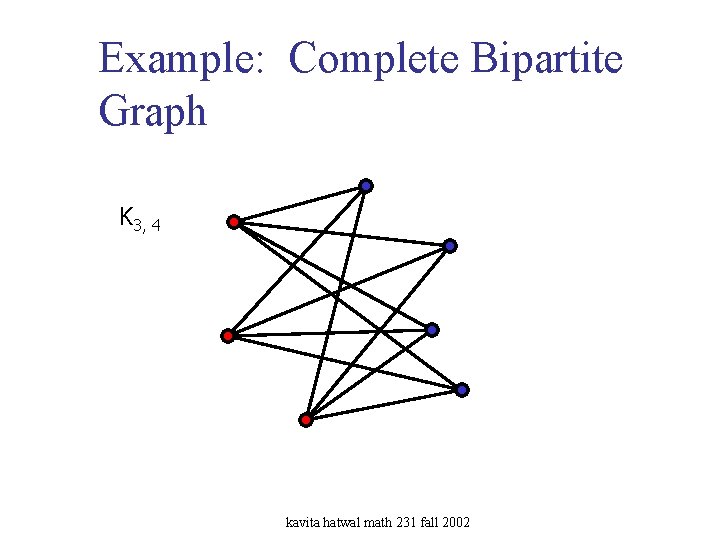
A graph with no vertices is called empty, and a one with at least one vertex is called non empty. Ø Page 604, 11. 1. 1, 11. 1. 2 Ø Page 608, 11. 1. 6, A complete graph with n vertices (denoted Kn) is a graph with n vertices in which each vertex is connected to each of the others (with one edge between each pair of vertices). A graph is bipartite if its vertices can be partitioned into two disjoint subsets U and V such that each edge connects a vertex from U to one from V. A bipartite graph is a complete bipartite graph if every vertex in U is connected to every vertex in V. If U has n elements and V has m, then we denote the resulting complete bipartite graph by Kn, m. Page 610, blue box kavita hatwal math 231 fall 2002

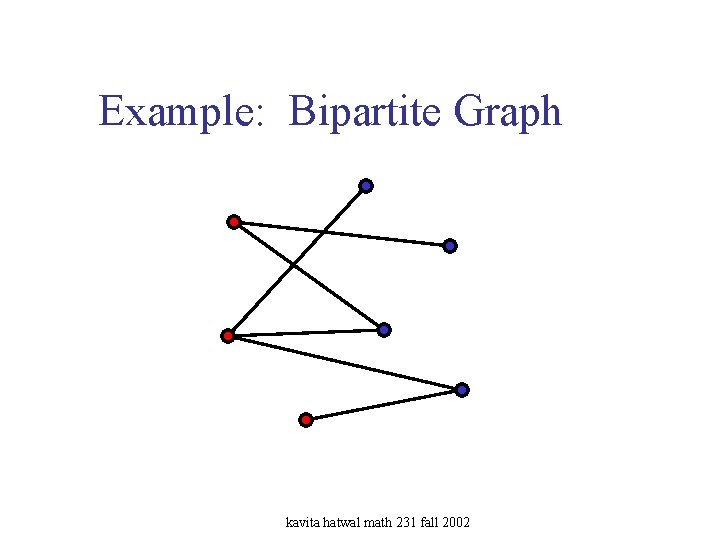
Example: Bipartite Graph kavita hatwal math 231 fall 2002

Example: Complete Bipartite Graph K 3, 4 kavita hatwal math 231 fall 2002

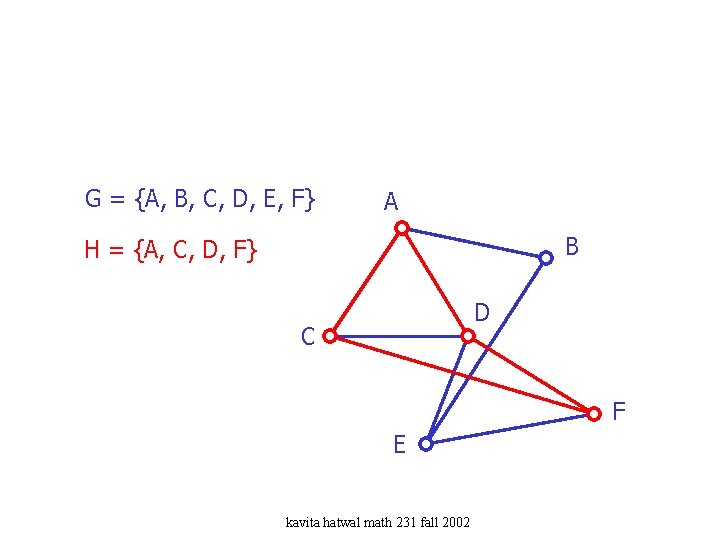
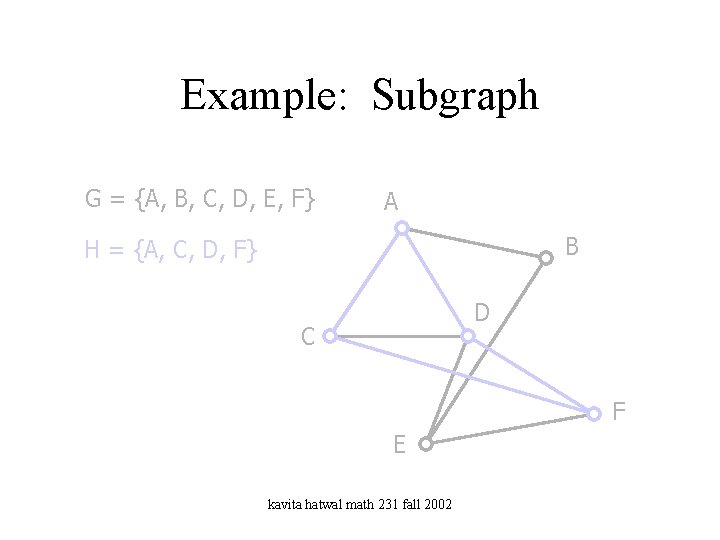
Subgraphs • A graph H = (V(H), E(H)) is a subgraph of a graph G = (V(G), E(G)) if V(H) V(G) and E(H) E(G). kavita hatwal math 231 fall 2002

G = {A, B, C, D, E, F} A B H = {A, C, D, F} D C F E kavita hatwal math 231 fall 2002

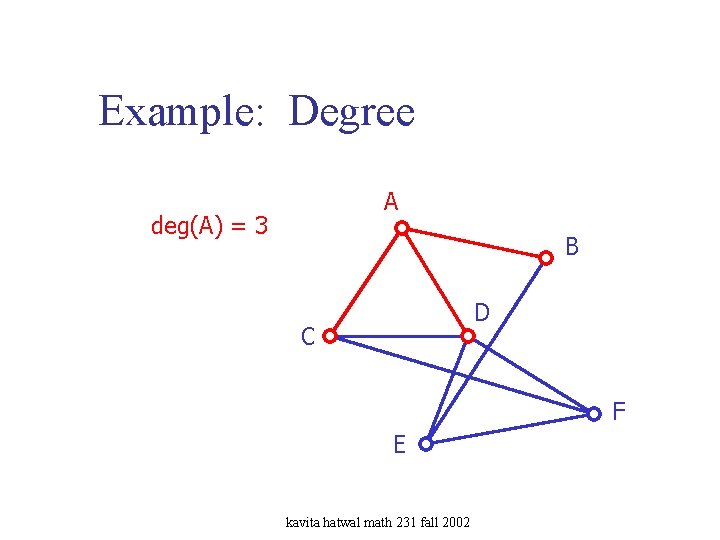
Degree of a Vertex • The degree of a vertex v is the number of edges that include v. – If the vertex has a loop, it is counted twice. • In a directed graph, – The in-degree of v is the number of edges directed into v. – The out-degree of v is the number of edges directed out of v. kavita hatwal math 231 fall 2002

Degree of a Vertex • The total degree of a graph G is the sum of the degrees of its vertices. kavita hatwal math 231 fall 2002

Example: Degree A deg(A) = 3 B D C F E kavita hatwal math 231 fall 2002

Handshaking Theorem The total degree of a graph is • 2 * (the number of edges in G) • is even. Corollary to the Handshaking Theorem: An undirected graph has an even number of vertices with an odd degree. kavita hatwal math 231 fall 2002

Is it possible to draw an undirected graph of 5 vertices with the following properties: deg(v 1) = 5, deg(v 2) = 2, deg(v 3) = 2, deg(v 4) = 1, deg(v 5) =3? • Answer (Version#1): Total degree =5+2+2+1+3 = 13 (odd!!!) …violates handshaking theorem. Therefore, such a graph is not possible. kavita hatwal math 231 fall 2002

Is it possible to draw an undirected graph of 5 vertices with the following properties: deg(v 1) = 5, deg(v 2) = 2, deg(v 3) = 2, deg(v 4) = 1, deg(v 5) = 3 ? • Answer: (Version#2: using corollary) How many vertices are there with odd degree? v 1, v 4, v 5 => 3 of them! But there must be an even number of odd degree vertices. Therefore such a graph is not possible to draw. kavita hatwal math 231 fall 2002

Given an undirected graph with 5 vertices and 7 edges, and that deg(v 1) = 3, deg(v 2) = 1, deg(v 3) = 5, deg(v 4) = 2, what is the degree of v 5? • Answer: Total degree = 3+1+5+2 + deg(v 5) = 2 x 7 (by handshaking theorem) Therefore deg(v 5) = 3 kavita hatwal math 231 fall 2002

In a group of 15 people, is it possible for each person to have exactly 3 friends? • Answer: The problem can be reduced to a graph problem. Each person is a vertex, therefore there are 15 vertices. We connect an edge between 2 vertices if they are friends. If a person has 3 friends, then every vertex has a degree of 3. Is such a graph possible? deg(v) = 15 x 3 = 45 (odd!) Therefore, not possible. vÎV kavita hatwal math 231 fall 2002

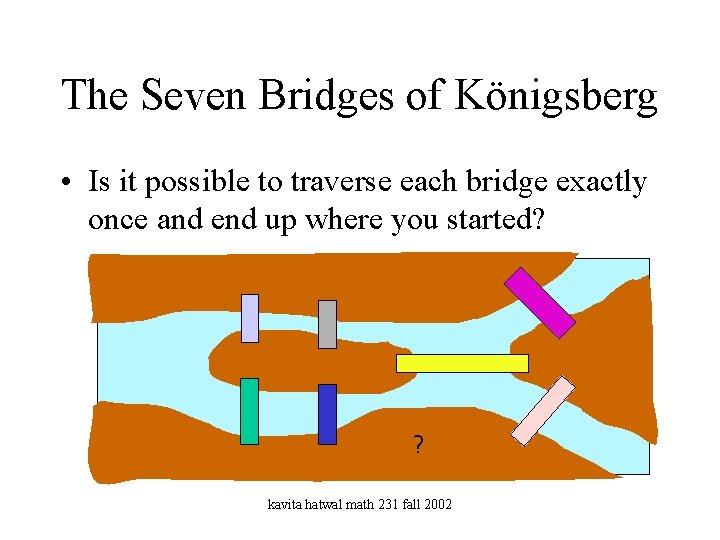
The Seven Bridges of Königsberg • Is it possible to traverse each bridge exactly once and end up where you started? ? kavita hatwal math 231 fall 2002

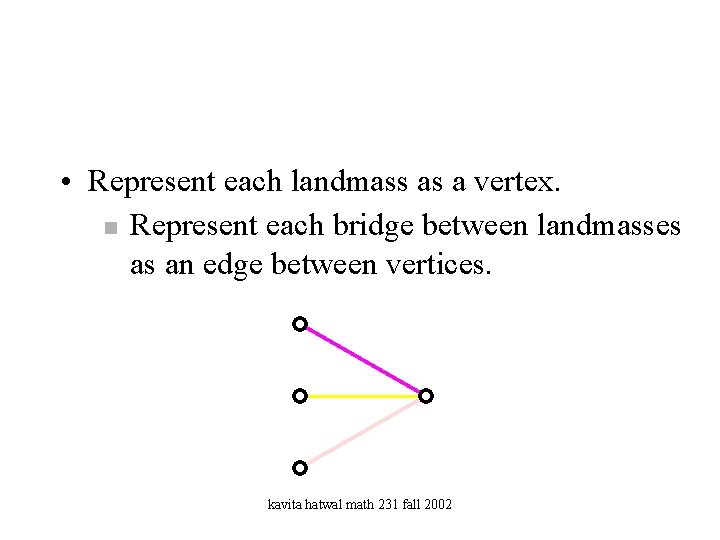
• Represent each landmass as a vertex. n Represent each bridge between landmasses as an edge between vertices. kavita hatwal math 231 fall 2002

• Let G be a graph with vertices v and w. • A walk from v to w is a finite alternating sequence of vertices and edges v 0 e 1 v 1 e 2 v 2…vn – 1 en – 1 vn where v 0 = v, vn = w, and each ei has endpoints vi – 1 and vi. kavita hatwal math 231 fall 2002

• A path from v to w is a walk from v to w in which the edges are distinct. • A simple path from v to w is a path from v to w in which the vertices are distinct. • A closed walk is a walk that starts and ends at the same vertex. kavita hatwal math 231 fall 2002

• A circuit is a closed path. • A simple circuit is a circuit in which the vertices are distinct, except for the first and last vertices. kavita hatwal math 231 fall 2002

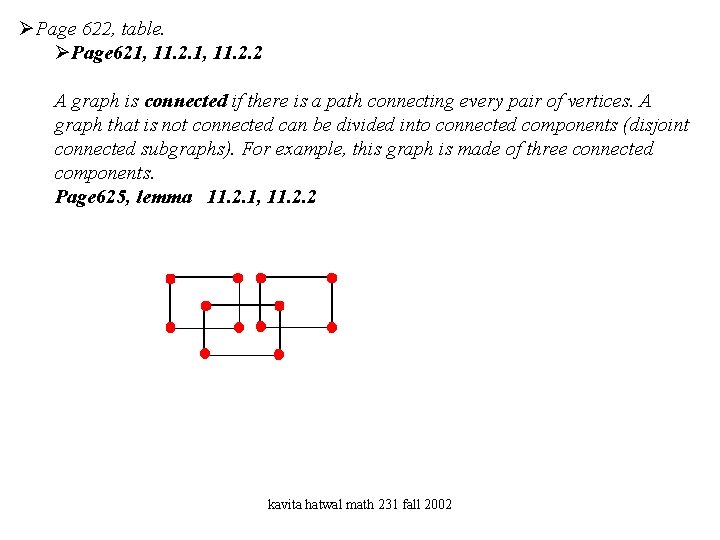
ØPage 622, table. ØPage 621, 11. 2. 2 A graph is connected if there is a path connecting every pair of vertices. A graph that is not connected can be divided into connected components (disjoint connected subgraphs). For example, this graph is made of three connected components. Page 625, lemma 11. 2. 1, 11. 2. 2 kavita hatwal math 231 fall 2002

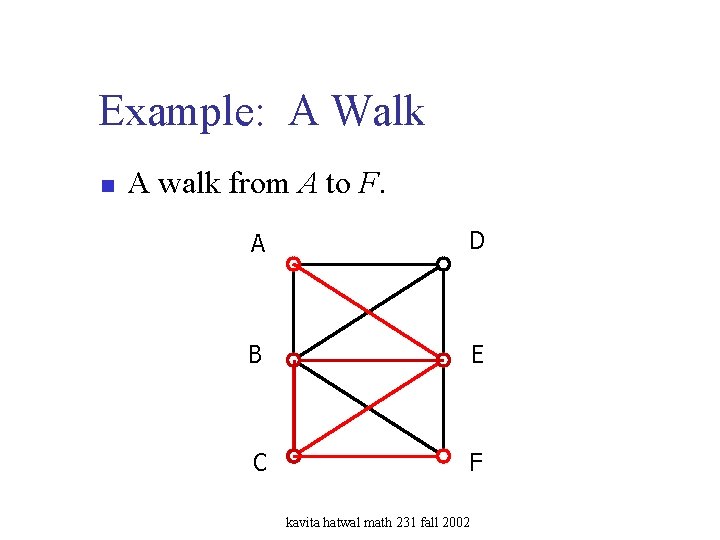
Example: A Walk n A walk from A to F. A D B E C F kavita hatwal math 231 fall 2002

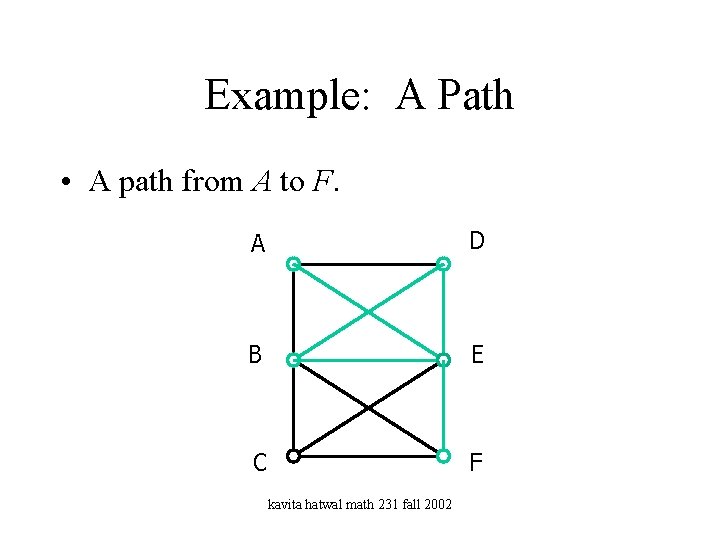
Example: A Path • A path from A to F. A D B E C F kavita hatwal math 231 fall 2002

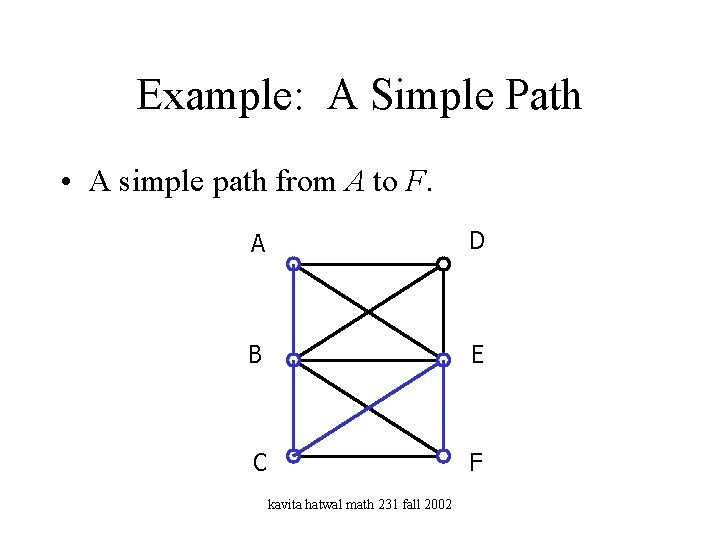
Example: A Simple Path • A simple path from A to F. A D B E C F kavita hatwal math 231 fall 2002

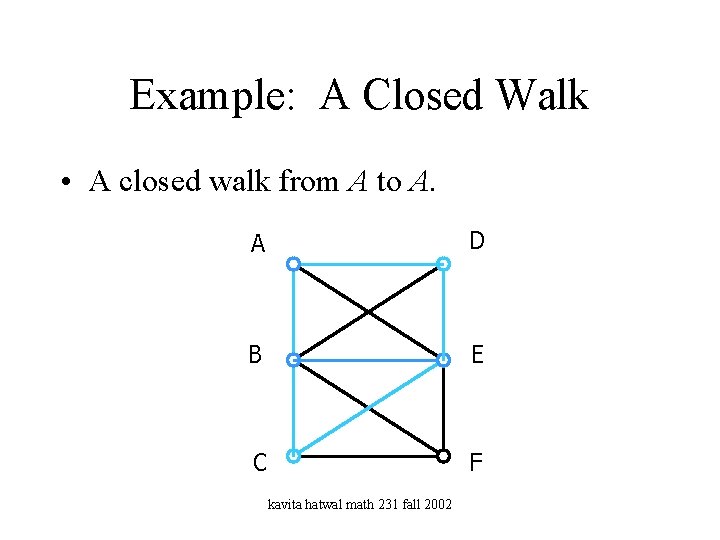
Example: A Closed Walk • A closed walk from A to A. A D B E C F kavita hatwal math 231 fall 2002

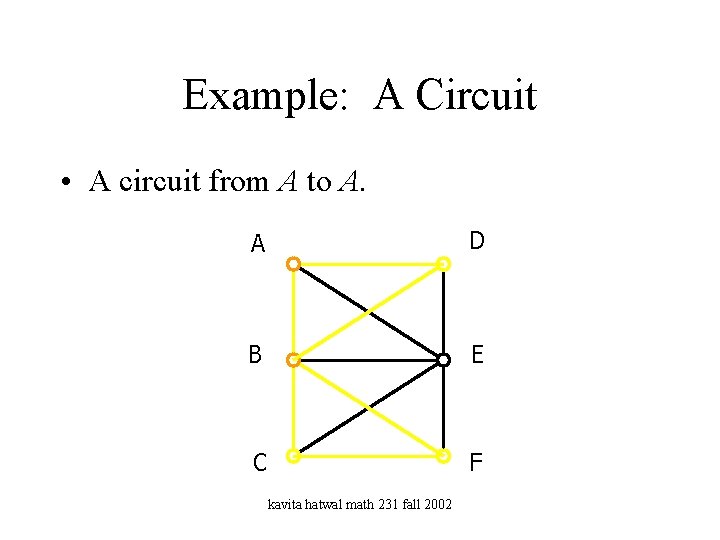
Example: A Circuit • A circuit from A to A. A D B E C F kavita hatwal math 231 fall 2002

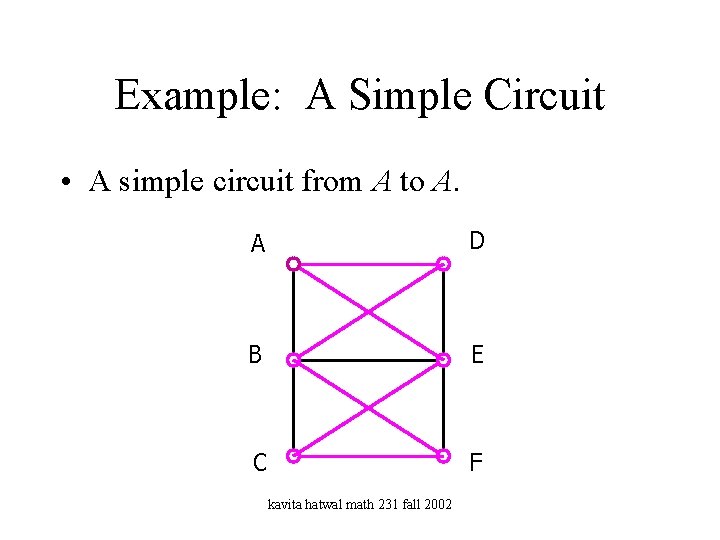
Example: A Simple Circuit • A simple circuit from A to A. A D B E C F kavita hatwal math 231 fall 2002

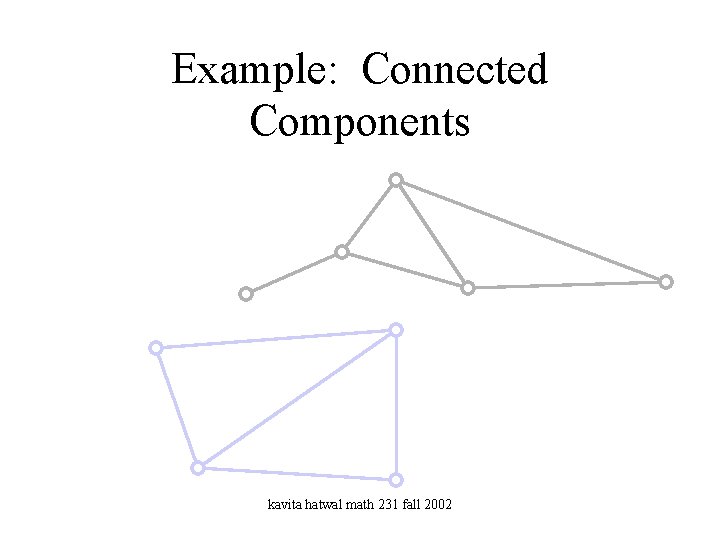
Example: Connected Components kavita hatwal math 231 fall 2002

Connected Graphs • Two vertices v and w of a graph G are connected if there is a walk from v to w. • A graph G is connected if every pair of vertices of G are connected. • A subgraph H of a graph G is a connected component of G if – H is connected, and – There is no connected subgraph K of G of which H is a proper subgraph. kavita hatwal math 231 fall 2002

Example: Connected Components kavita hatwal math 231 fall 2002

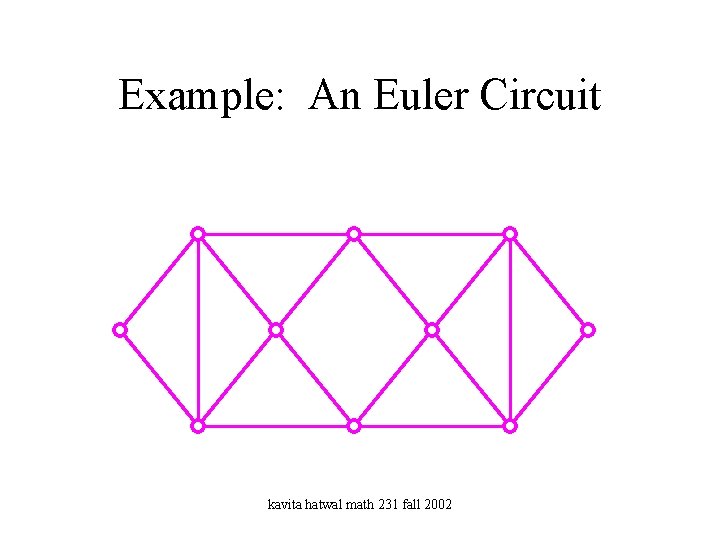
Euler Circuits • An Euler circuit of a graph G is a circuit that contains every vertex of G at least once and every edge of G exactly once. kavita hatwal math 231 fall 2002

Example: An Euler Circuit kavita hatwal math 231 fall 2002

Example: Subgraph G = {A, B, C, D, E, F} A B H = {A, C, D, F} D C F E kavita hatwal math 231 fall 2002

Origin of Problem In the town of Konigsberg there was an island in the river connected by seven bridges to the rest of the city. The question was whether you could find a path starting and ending at the same spot, that crossed each bridge exactly once. Solution of Problem This problem was solved by Euler, who represented each bridge as an edge, and each terminal point of a bridge as a node in a graph. Then he found a necessary and sufficient condition on each of the nodes: each node must have even degree (even number of edges incident to it). (page 620). All nodes have odd degree. So it is impossible to find a closed path that uses each edge exactly once. Euler's Theorem Let G be a connected graph (every pair of nodes is joined by some path). Then a necessary and sufficient condition for G to have an Euler circuit is that each node of G has even degree. So if a graph has an euler circuit, then every vertex of the graph has even degree. If some vertex of a graph has odd degree, then the graph does not have an Euler circuit. kavita hatwal math 231 fall 2002

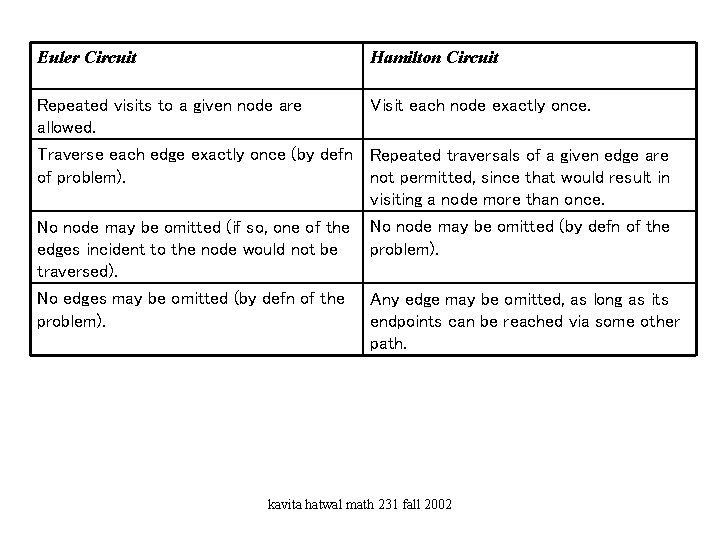
Hamilton Circuits A seemingly related problem is the Hamiltonian circuit problem. Here, goal is to traverse the entire graph, starting at node a and visiting each node exactly once, before returning to a. Notice this means you cannot traverse a given edge more than once (Exception: G has only two nodes), for then you would be visiting at least one of the endpoints of that edge more than once. So in this sense, the Hamilton Circuit problem is more demanding than the Euler circuit problem. kavita hatwal math 231 fall 2002

Euler Circuit Hamilton Circuit Repeated visits to a given node are allowed. Visit each node exactly once. Traverse each edge exactly once (by defn Repeated traversals of a given edge are of problem). not permitted, since that would result in visiting a node more than once. No node may be omitted (if so, one of the edges incident to the node would not be traversed). No node may be omitted (by defn of the problem). No edges may be omitted (by defn of the problem). Any edge may be omitted, as long as its endpoints can be reached via some other path. kavita hatwal math 231 fall 2002

Unlike the Euler circuit problem, finding Hamilton circuits is hard. There is no simple set of necessary and sufficient conditions, and no simple algorithm. But here is a list of conditions that must be satisfied: Necessary conditions for Hamilton circuit Assume G has more than 2 nodes. 1. No vertex of degree 1 If a has degree 1, then the other endpoint of the edge incident to a must be visited at least twice in any circuit of G. 2. If a node has degree 2, then both edges incident to it must be in any Hamilton circuit. 3. No smaller circuits contained in any Hamilton circuit (the start/endpoint of any smaller circuit would have to be visited twice). 4. There must exist a subgraph H of G with the following properties: 5. H contains every vertex of G 6. H is connected 7. H has the same number of edges as vertices 8. H has every node with degree 2 9. The subgraph H is the Hamilton circuit in the graph G. Page 634 Prop 11. 2. 6 kavita hatwal math 231 fall 2002

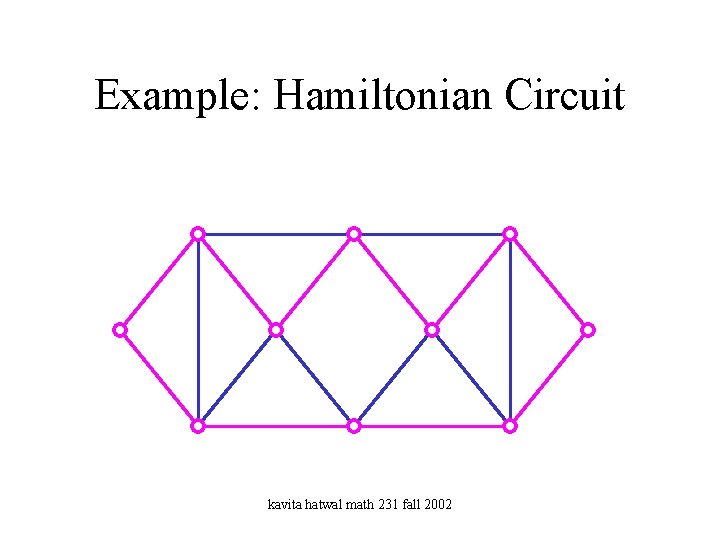
Example: Hamiltonian Circuit kavita hatwal math 231 fall 2002

Travelling Salesperson Problem Page 635, 11. 2. 9 This is a famous problem. It goes like this: 1. A salesperson has a route among n cities. 2. He/she would like to visit all the cities, but in a way to minimize the total distance travelled. This is a weighted Hamilton circuit problem. You have to find a route that visits each city exactly once, but in addition, the edges connecting the cities are weighted according to the distances between those cities. So you want the sum of the edge weights to be minimized. Graph representation of problem The problem translates into finding the minimum weighted Hamiltonian circuit in a connected graph on n vertices. It is difficult because: 1. There is no simple algorithm for finding a hamiltonian circuit. 2. Among hamiltonian circuits, the best you can do is compute the "weight" (summed distance) of each, and find the min. For a complete graph on n nodes, there are n! different hamiltonian circuits. Comparing them all is beyond the range of any known (or possible) computer, when n gets large. kavita hatwal math 231 fall 2002

Matrix representations of graphs What is a matrix? An a (read “m by n”)matrix over a set A is a rectangular array of elements of S arranged into m rows and n columns. i’th row of A j’th column of A kavita hatwal math 231 fall 2002

kavita hatwal math 231 fall 2002

Equal Matrix Two matrices A and B are said to be equal , if both A and B have the same size and the corresponding entries are equal. That is, aij=bij for all i = 1, 2, …, n and j = 1, 2, …, n Square matrix If a matrix A has n rows and n columns then we say it's a square matrix. In a square matrix the elements ai, i , with i = 1, 2, 3, . . . , are called diagonal elements. Diagonal matrix A diagonal matrix is a square matrix with all non-diagonal elements 0. The diagonal matrix is completely denoted by the diagonal elements. Example. [7 0 0] [0 5 0] [0 0 6] The matrix is denoted by diag(7 , 5 , 6) An identity matrix I is a diagonal matrix with all diagonal element = 1. The tranpose of a matrix The n x m matrix A' is the transpose of the m x n matrix A if and only if The ith row of A = the ith column of A' for (i = 1, 2, 3, . . n) kavita hatwal math 231 fall 2002 So ai, j = aj, i'

A symmetric matrix A square matrix is called symmetric if it is equal to its transpose. Then ai, j = aj, i , for all i and j. Page 641 #11. 3. 1 Multiplication of a row matrix by a column matrix This multiplication is only possible if the row matrix and the column matrix have the same number of elements. The result is a ordinary number ( 1 x 1 matrix). To multiply the row by the column, one multiplies corresponding elements, then adds the results. Example. [2 1 3] [1] [2] = [19] [5] Multiplication of two matrices A. B This product is defined only if A is a (l x m) matrix and B is a (m x n) matrix. So the number of columns of A has to be equal to the number of rows of B. The product C = A. B then is a (l x n) matrix. The element of the ith row and the jth column of the product is found by multiplying the ith row of A by the jth column of B. ci, j = sumk (ai, k. bk, j) kavita hatwal math 231 fall 2002

Example. Is matrix multiplication commutative? But matrix multiplication is associative. That is A(BC) = (AB)C Definition For any square matrix A, the powers of A are defined as follows: Where I is the identity matrix for all integers n 1 kavita hatwal math 231 fall 2002

Matrices and directed graphs Graphs can also be represented in the form of matrices. The major advantage of matrix representation is that the calculation of paths and cycles can easily be performed using well known operations of matrices. However, the disadvantage is that this form of representation takes away from the visual aspect of graphs. It would be difficult to illustrate in a matrix, properties that are easily illustrated graphically. Page 641, figure 11. 3. 1 An adjacency matrix is defined as follows: Let G be a graph with "n" vertices that are assumed to be ordered from v 1 to vn. The n x n matrix A, in which aij= 1 if there exists a path from vi to vj aij = 0 otherwise is called an adjacency matrix. • directed graphs and equivalence relations of a binary relation. kavita hatwal math 231 fall 2002

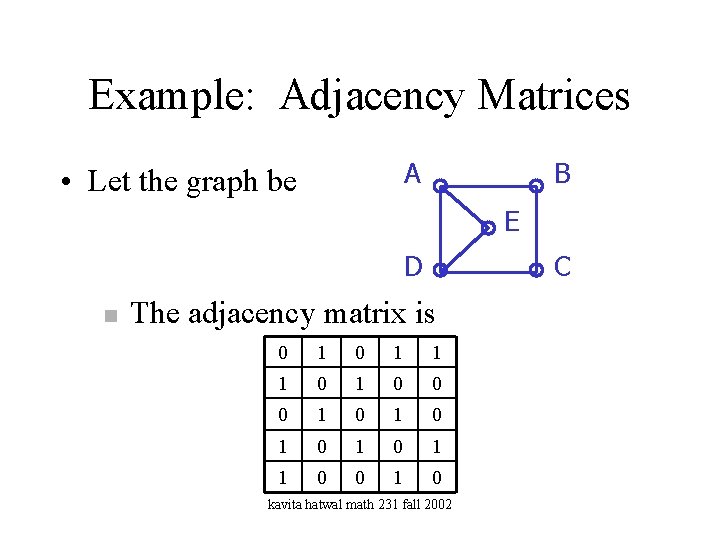
Example: Adjacency Matrices A • Let the graph be B E D n C The adjacency matrix is 0 1 1 1 0 0 0 1 0 1 0 1 1 0 0 1 0 kavita hatwal math 231 fall 2002

• Theorem: Let G be a simple graph. Then – The adjacency matrix of G is symmetric. – The main diagonal is 0. – The degree of vertex vi is the sum of the elements of row i (or column i). kavita hatwal math 231 fall 2002

• The adjacency matrix is n 0 1 1 1 0 0 0 1 0 1 0 1 1 0 0 1 0 The row totals are 3, 2, 2, 3, 2, which are the same as the degrees of the vertices. kavita hatwal math 231 fall 2002

• Theorem: Let G be a simple digraph and let A be the adjacency matrix of G. Then – The indegree of vi equals the sum of column i. – The outdegree of vi equals the sum of row i. • Matrices and connected components. Page 645 kavita hatwal math 231 fall 2002

Counting Walks • Theorem: Let G be a graph and let A be the adjacency matrix of G. Then the (i, j)-element of An equals the number of walks of length n from vi to vj. • The existence of an edge between two vertices vi and vj is shown by an entry of 1 in the ith row and jth column of the adjacency matrix. This entry represents a walk of length 1 from vi to vj. • To compute a walk of length 2, the matrix of length 1 must be multiplied by itself, and the product matrix is the matrix representation of path of length 2. kavita hatwal math 231 fall 2002

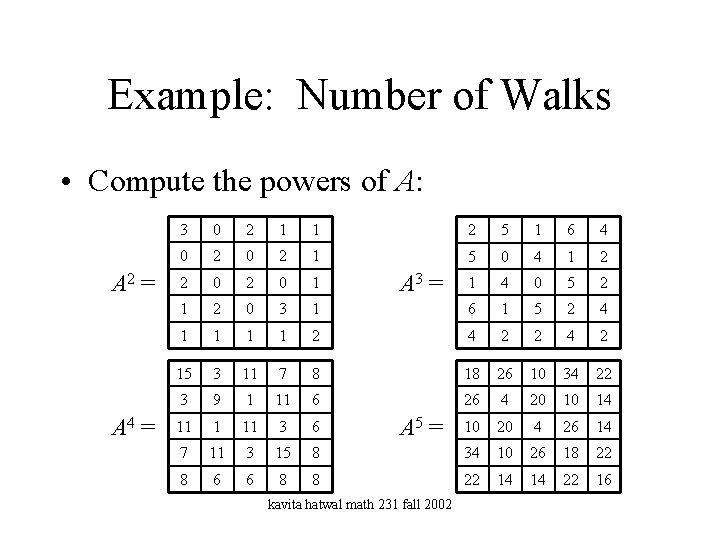
Example: Number of Walks • Let G be the graph with adjacency matrix n 0 1 1 1 0 0 0 1 0 1 0 1 1 0 0 1 0 Find the number of walks of length 2, 3, 4, and 5 from A to D. kavita hatwal math 231 fall 2002

Example: Number of Walks • Compute the powers of A: A 2 = A 4 = 3 0 2 1 1 2 5 1 6 4 0 2 1 5 0 4 1 2 2 0 1 1 4 0 5 2 1 2 0 3 1 6 1 5 2 4 1 1 2 4 2 15 3 11 7 8 18 26 10 34 22 3 9 1 11 6 26 4 20 10 14 11 1 11 3 6 10 20 4 26 14 7 11 3 15 8 34 10 26 18 22 8 6 6 8 8 22 14 14 22 16 A 3 = A 5 = kavita hatwal math 231 fall 2002

Example: Number of Walks • Thus, for example, there are 34 walks of length 5 from A to D. • What are they? – A-B-A-D – A-B-A-E-A-D – A-B-C-B-A-D – A-B-A-D – etc. kavita hatwal math 231 fall 2002

page 651, example 11. 3. 10 kavita hatwal math 231 fall 2002

Trees • • • a graph with no cycles is called acyclic forest— acyclic undirected graph, possibly unconnected dag —- directed acyclic graph tree (sometimes free tree) —connected forest A tree is a graph that is connected and circuit-free kavita hatwal math 231 fall 2002

1. 1 Definition: Let G=(V, E). G is a tree IFF (a) G is connected; and (b) G does not have any circuits (acyclic). Comment: • difference between trivial and non-trivial circuits. • A trivial circuit as a circuit of length 0. • All trees are bipartite graphs kavita hatwal math 231 fall 2002

Definition: Let G=(V, E). G is a tree IFF (a) G is connected; and (b) G does not have any circuits (acyclic). Example of a tree kavita hatwal math 231 fall 2002

Trees • Theorem: A tree with at least two vertices contains at least one vertex of degree 1. • Proof: – Begin a simple path at any vertex. – Since G is circuit-free, the path must terminate at a dead-end. – That dead-end will be a vertex of degree 1. kavita hatwal math 231 fall 2002

• Theorem: A nonempty tree with n vertices contains exactly n – 1 edges. • Proof (Induction on n): • Basic Step – Let T be a tree with 1 vertex v. – Any edge must go from v to v, which would be a circuit. – Therefore, T contains 0 edges. kavita hatwal math 231 fall 2002

• Inductive Step – Suppose that, for some n 1, every tree with n vertices has exactly n – 1 edges. – Let T be a tree with n + 1 vertices. – Let v be a vertex of degree 1. – Remove v and its incident edge from the graph. – The remaining subgraph is connected and circuitfree. kavita hatwal math 231 fall 2002

– Therefore, it is a tree with n vertices. – So, it has exactly n – 1 edges. – Since we removed one edge from T, that means that T has n edges. • Therefore, for all n 1, a tree with n vertices has exactly n – 1 edges. kavita hatwal math 231 fall 2002

Properties of a Tree • Theorem: Let G be a graph with n vertices and let p, q, and r be the following statements. – p : G is connected. – q : G is circuit-free. – r : G has exactly n – 1 edges. Then – p q r. – p r q. – q r p. kavita hatwal math 231 fall 2002

Proof, continued • Proof: G is connected AND G is circuit-free • Suppose that G is connected and G is circuit -free. – We have already proven that G must have exactly n – 1 edges. kavita hatwal math 231 fall 2002

Proof, continued • Suppose that G is connected and G has exactly n – 1 edges. – Suppose G contains a circuit. – Then remove an edge to break the circuit. – Continue to remove edges in this way until the resulting graph is circuit-free. – Then the resulting graph is connected and circuit-free, but contains fewer than n – 1 edges. kavita hatwal math 231 fall 2002

Proof, continued – This is a contradiction. – Therefore, G must be circuit-free. kavita hatwal math 231 fall 2002

Proof, continued • Suppose that G is circuit-free and G has exactly n – 1 edges. – Suppose G is not connected. – Then add an edge connecting two of its connected components. – Continue adding edges in this manner until the resulting graph is connected. – None of these edges will create a circuit. kavita hatwal math 231 fall 2002

Proof, concluded – Therefore, the resulting graph will be connected and circuit-free, but it will contain more than n – 1 edges. – This is a contradiction. – Therefore, G must have been connected. kavita hatwal math 231 fall 2002

Expression Trees • An expression tree represents an algebraic expression. – Each internal node represents an operator. – Each terminal node represents a number or a variable. – At each internal node, the left subtree represents the left operand the right subtree represents the right operand. kavita hatwal math 231 fall 2002

A rooted tree is a free tree in which one vertex is distinguished from the others. • the distinguished vertex is called the root • vertices in a rooted tree are often called nodes Let r be the root of a rooted tree T. Note that for any node x, there is a unique path from r to x. • any node y on path from r to x is called an ancestor of x. • If y is an ancestor of x, x is called the descendent of y. root is only node with no parent siblings —two nodes which share the same parent external node or leaf —node with no children internal node – nonleaf node Number of children of a node x in a rooted tree T is called the degree of x. Length of the path from r to x is called the depth of x. largest depth of any node in a tree T is called the height of T kavita hatwal math 231 fall 2002

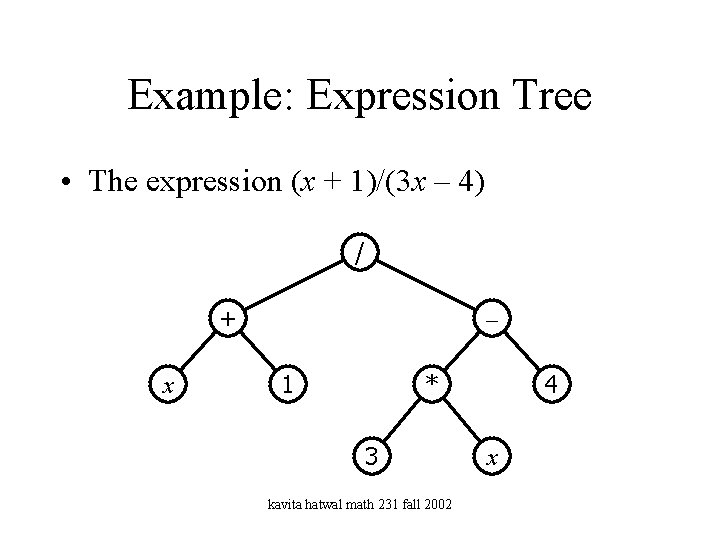
Example: Expression Tree • The expression (x + 1)/(3 x – 4) / + x – 1 * 3 kavita hatwal math 231 fall 2002 4 x

Expression Trees • If an operator is unary, then – It has a left subtree if it is postfix. – It has a right subtree if it is prefix. kavita hatwal math 231 fall 2002

Example: Expression Tree • Represent the expression –(x + 3)4. – ^ + x 4 3 kavita hatwal math 231 fall 2002

Binary Search Trees • A binary search tree is a binary tree with the following logical structure. • At each node – The values in the left subtree are less than or equal to the value at the node. – The values in the right subtree are greater than or equal to the value at the node. kavita hatwal math 231 fall 2002

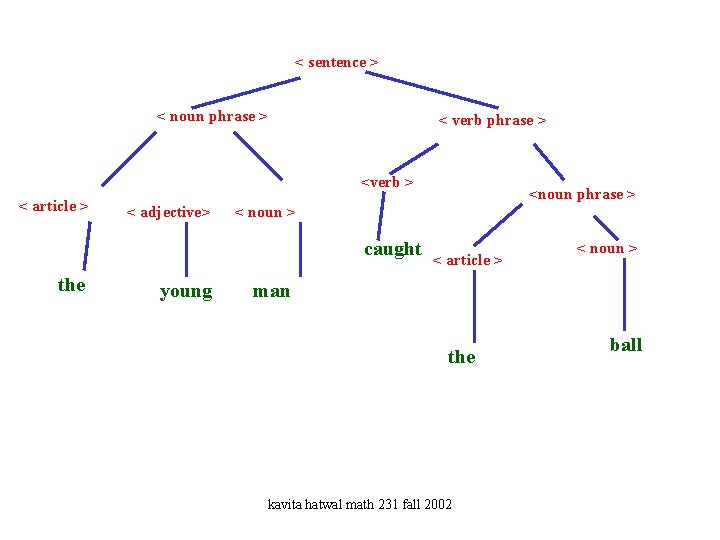
• • • Syntax (or grammatical structure)of natural languages such as English. Has proved useful in constructing compilers for high level computer languages. You define the grammar rules of the language that you’re designing at the very onset. These grammar rules ( also called productions) are expressed using a shorthand notation called Backus-Naur notation. In BNF, | represents OR and <> are used to enclose terms to be defined. A very small subset of English grammar can be listed in BNF and applied to a sentence “The young man caught the ball” 1. <sentence> <noun phrase> <verb phrase> 2. , 3. < noun phrase > <article> <noun>| <article> <adjective> <noun> 4. <verb phrase> <verb> <noun phrase> 5. <article> the 6. <adjective> young 7. <noun> man|ball 8. <verb> caught kavita hatwal math 231 fall 2002

< sentence > < noun phrase > < verb phrase > <verb > < article > < adjective> < noun > caught the young <noun phrase > < article > < noun > man the kavita hatwal math 231 fall 2002 ball

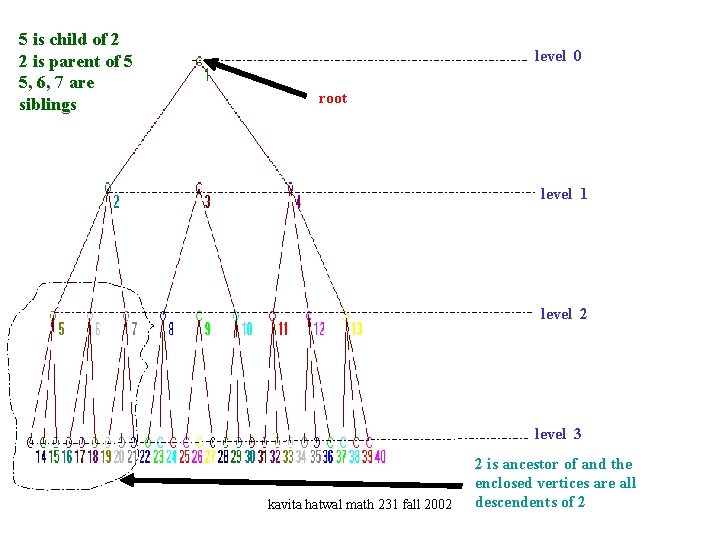
5 is child of 2 2 is parent of 5 5, 6, 7 are siblings level 0 root level 1 level 2 level 3 kavita hatwal math 231 fall 2002 2 is ancestor of and the enclosed vertices are all descendents of 2

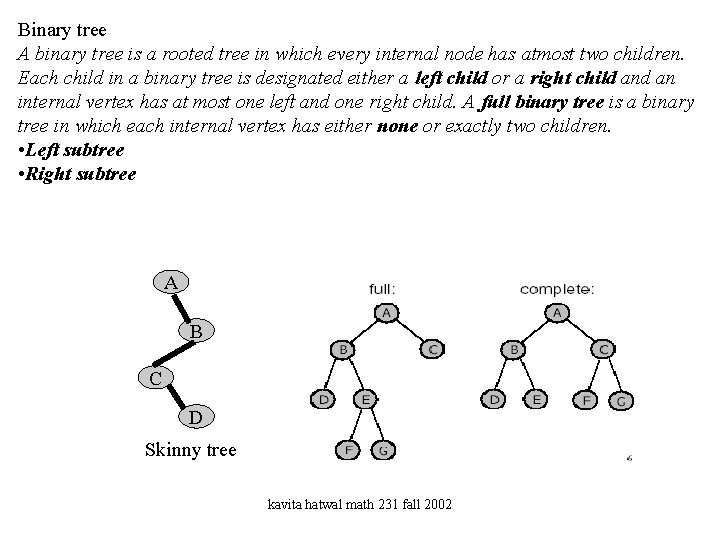
Binary tree A binary tree is a rooted tree in which every internal node has atmost two children. Each child in a binary tree is designated either a left child or a right child an internal vertex has at most one left and one right child. A full binary tree is a binary tree in which each internal vertex has either none or exactly two children. • Left subtree • Right subtree A B C D Skinny tree kavita hatwal math 231 fall 2002

Binary trees are often used to represent algebraic expressions. Binary trees allow for an "inorder" traversal, where each node is visited after its left child, but before its right child. The preorder, inorder, and postorder traversals of an expression tree will print a prefix, infix, or postfix expression, respectively. • Inorder: visit left subtree, then the root, then the right subtree. • Preorder: visit root, left, right. + • Postorder: visit left, right, root. Preorder: + * 3 7 ^ 4 2 Inorder: 3 * 7 + 4 ^ 2 Postorder: 3 7 * 4 2 ^ + ^ * 3 7 4 2 / + a More generally, the binary tree represents a/(c+d). • The internal vertices are arithmetic operators. • Terminal vertices are variables. c • Operator at each vertex acts on its left and right subtree in left-right order kavita hatwal math 231 fall 2002 d

Full m-ary Trees (Definition) • A m-ary tree is FULL iff every vertex has either 0 or m children. (OR every internal vertex has m children). • Examples of full binary trees. Full Tree? Yes No Yes kavita hatwal math 231 fall 2002 No

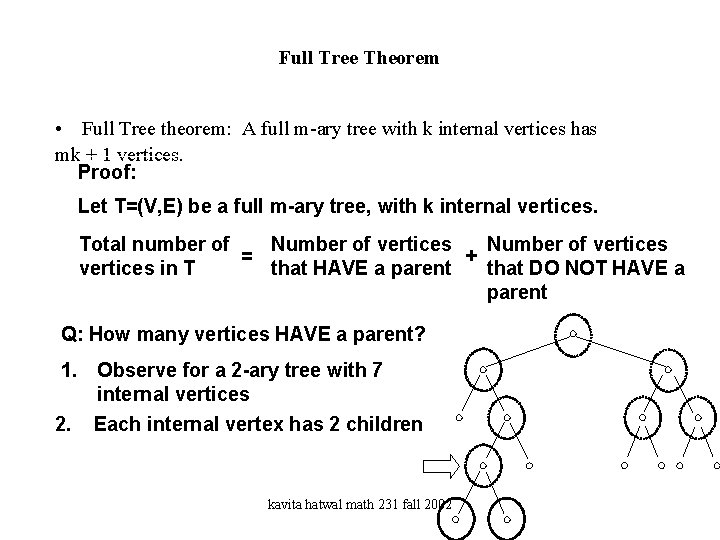
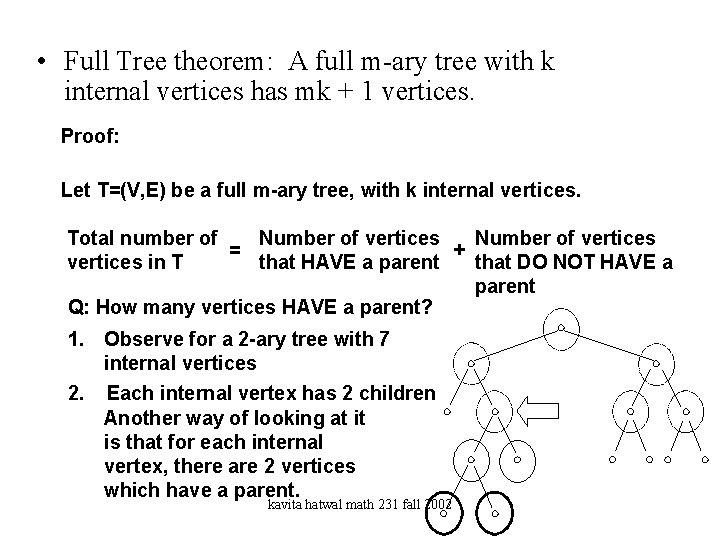
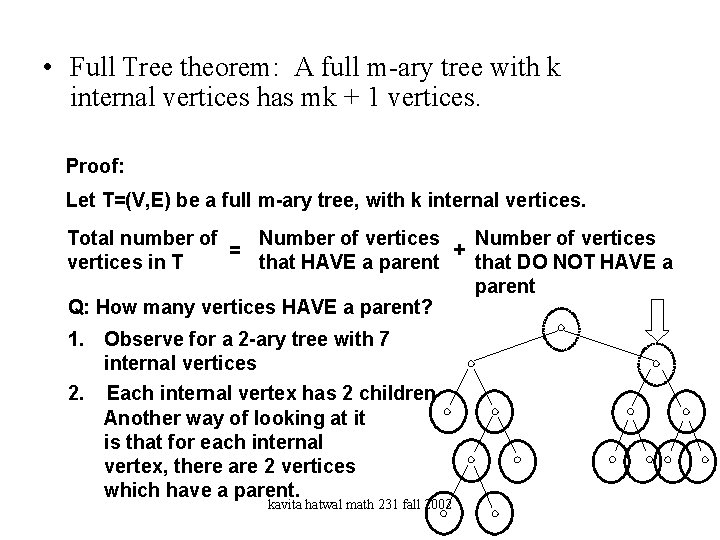
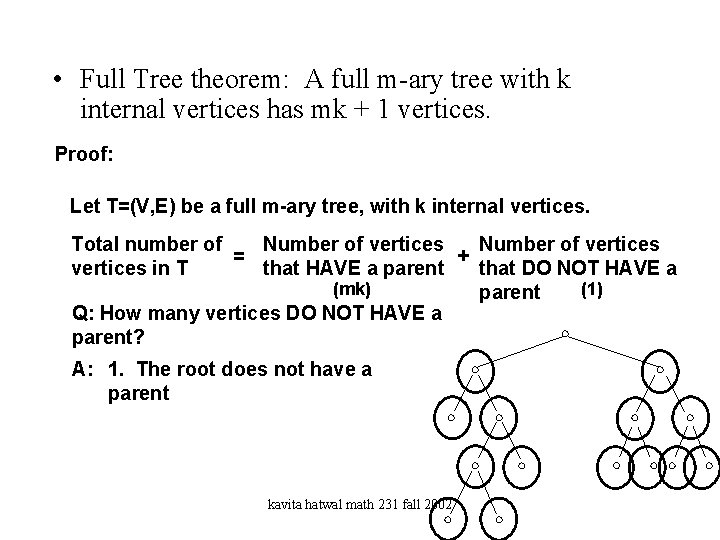
Full Tree Theorem • Full Tree theorem: A full m-ary tree with k internal vertices has mk + 1 vertices. Proof: Let T=(V, E) be a full m-ary tree, with k internal vertices. Total number of Number of vertices = + vertices in T that HAVE a parent that DO NOT HAVE a parent Q: How many vertices HAVE a parent? 1. Observe for a 2 -ary tree with 7 internal vertices 2. Each internal vertex has 2 children kavita hatwal math 231 fall 2002

• Full Tree theorem: A full m-ary tree with k internal vertices has mk + 1 vertices. Proof: Let T=(V, E) be a full m-ary tree, with k internal vertices. Total number of Number of vertices = + vertices in T that HAVE a parent that DO NOT HAVE a parent Q: How many vertices HAVE a parent? 1. Observe for a 2 -ary tree with 7 internal vertices 2. Each internal vertex has 2 children Another way of looking at it is that for each internal vertex, there are 2 vertices which have a parent. kavita hatwal math 231 fall 2002

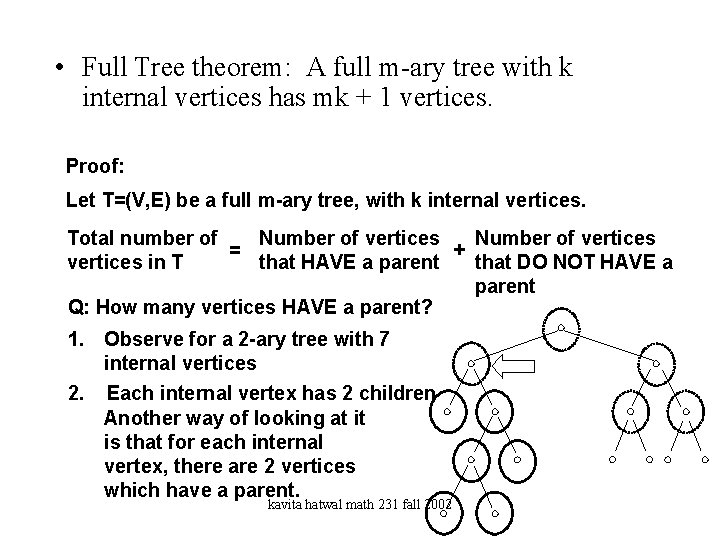
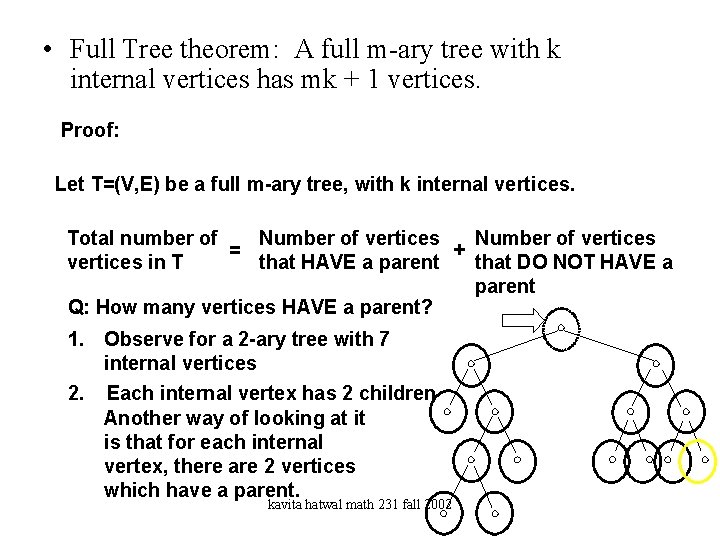
• Full Tree theorem: A full m-ary tree with k internal vertices has mk + 1 vertices. Proof: Let T=(V, E) be a full m-ary tree, with k internal vertices. Total number of Number of vertices = + vertices in T that HAVE a parent that DO NOT HAVE a parent Q: How many vertices HAVE a parent? 1. Observe for a 2 -ary tree with 7 internal vertices 2. Each internal vertex has 2 children Another way of looking at it is that for each internal vertex, there are 2 vertices which have a parent. kavita hatwal math 231 fall 2002

• Full Tree theorem: A full m-ary tree with k internal vertices has mk + 1 vertices. Proof: Let T=(V, E) be a full m-ary tree, with k internal vertices. Total number of Number of vertices = + vertices in T that HAVE a parent that DO NOT HAVE a parent Q: How many vertices HAVE a parent? 1. Observe for a 2 -ary tree with 7 internal vertices 2. Each internal vertex has 2 children Another way of looking at it is that for each internal vertex, there are 2 vertices which have a parent. kavita hatwal math 231 fall 2002

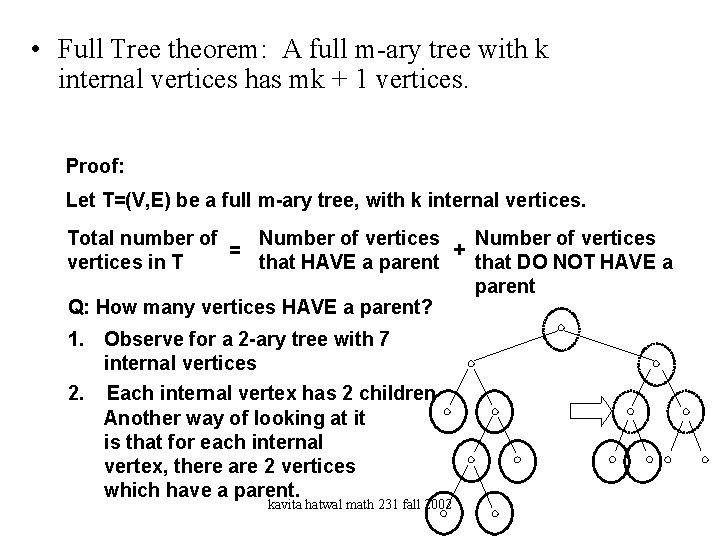
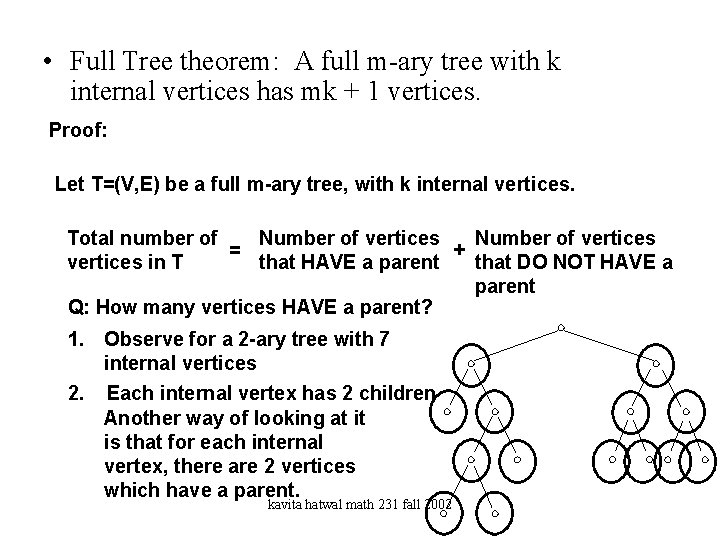
• Full Tree theorem: A full m-ary tree with k internal vertices has mk + 1 vertices. Proof: Let T=(V, E) be a full m-ary tree, with k internal vertices. Total number of Number of vertices = + vertices in T that HAVE a parent that DO NOT HAVE a parent Q: How many vertices HAVE a parent? 1. Observe for a 2 -ary tree with 7 internal vertices 2. Each internal vertex has 2 children Another way of looking at it is that for each internal vertex, there are 2 vertices which have a parent. kavita hatwal math 231 fall 2002

• Full Tree theorem: A full m-ary tree with k internal vertices has mk + 1 vertices. Proof: Let T=(V, E) be a full m-ary tree, with k internal vertices. Total number of Number of vertices = + vertices in T that HAVE a parent that DO NOT HAVE a parent Q: How many vertices HAVE a parent? 1. Observe for a 2 -ary tree with 7 internal vertices 2. Each internal vertex has 2 children Another way of looking at it is that for each internal vertex, there are 2 vertices which have a parent. kavita hatwal math 231 fall 2002

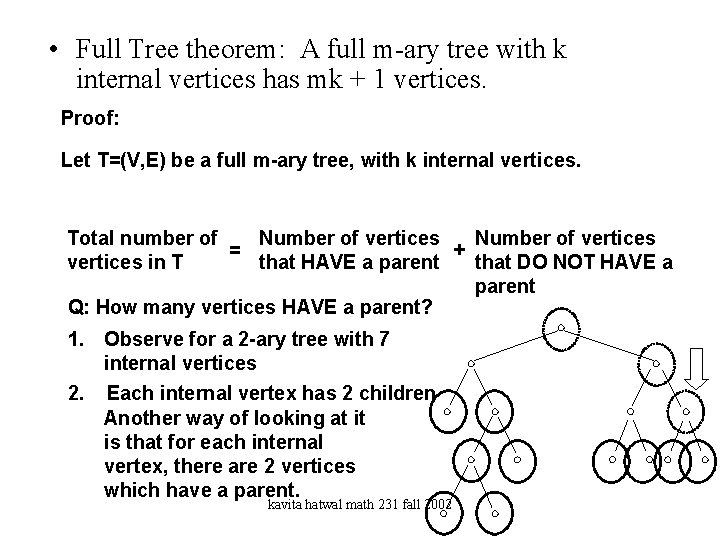
• Full Tree theorem: A full m-ary tree with k internal vertices has mk + 1 vertices. Proof: Let T=(V, E) be a full m-ary tree, with k internal vertices. Total number of Number of vertices = + vertices in T that HAVE a parent that DO NOT HAVE a parent Q: How many vertices HAVE a parent? 1. Observe for a 2 -ary tree with 7 internal vertices 2. Each internal vertex has 2 children Another way of looking at it is that for each internal vertex, there are 2 vertices which have a parent. kavita hatwal math 231 fall 2002

• Full Tree theorem: A full m-ary tree with k internal vertices has mk + 1 vertices. Proof: Let T=(V, E) be a full m-ary tree, with k internal vertices. Total number of Number of vertices = + vertices in T that HAVE a parent that DO NOT HAVE a parent Q: How many vertices HAVE a parent? 1. Observe for a 2 -ary tree with 7 internal vertices 2. Each internal vertex has 2 children Another way of looking at it is that for each internal vertex, there are 2 vertices which have a parent. kavita hatwal math 231 fall 2002

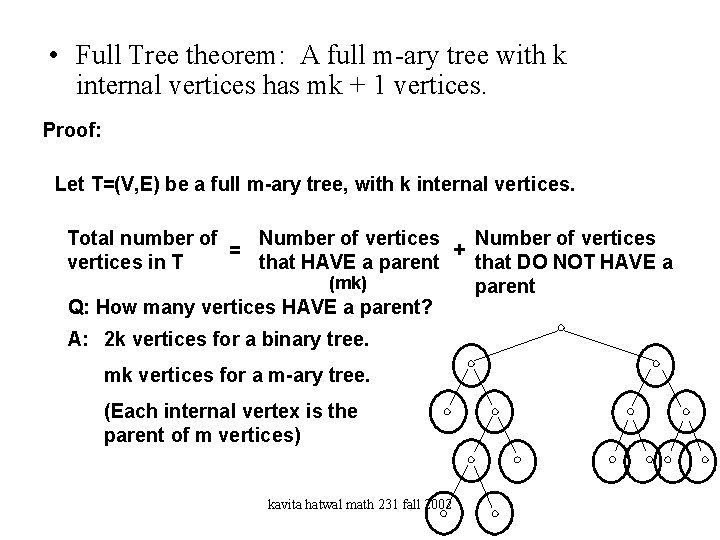
• Full Tree theorem: A full m-ary tree with k internal vertices has mk + 1 vertices. Proof: Let T=(V, E) be a full m-ary tree, with k internal vertices. Total number of Number of vertices = + vertices in T that HAVE a parent that DO NOT HAVE a (mk) parent Q: How many vertices HAVE a parent? A: 2 k vertices for a binary tree. mk vertices for a m-ary tree. (Each internal vertex is the parent of m vertices) kavita hatwal math 231 fall 2002

• Full Tree theorem: A full m-ary tree with k internal vertices has mk + 1 vertices. Proof: Let T=(V, E) be a full m-ary tree, with k internal vertices. Total number of Number of vertices = + vertices in T that HAVE a parent that DO NOT HAVE a (mk) (1) parent Q: How many vertices DO NOT HAVE a parent? A: 1. The root does not have a parent kavita hatwal math 231 fall 2002

• Full Tree theorem: A full m-ary tree with k internal vertices has mk + 1 vertices. Proof: Let T=(V, E) be a full m-ary tree, with k internal vertices. Total number of Number of vertices = + vertices in T that HAVE a parent that DO NOT HAVE a (mk) (1) parent = mk + 1 kavita hatwal math 231 fall 2002

• Leaves-Height Theorem for Binary Trees: Let T=(V, E) be a binary tree that has t leaves, and height h. Then t £ 2 h. Proof: (by using induction on the height of the tree) Base Case: h = 0 T has 1 vertex, which is a leaf. t = 1 £ 1 = 20 = 2 h Base case is true. kavita hatwal math 231 fall 2002

• Leaves-Height Theorem for Binary Trees: Let T=(V, E) be a binary tree that has t leaves, and height h. Then t £ 2 h. Proof: (by using induction on the height of the tree) Inductive Case: Assume that t £ 2 h for h = 0, 1, 2, …, k (STRONG!) Let T be any binary tree of height k+1. (Need to show t £ 2 k+1) With respect to the root vertex, let the left and right subtrees be TL and TR respectively. 1 Let the number of leaves in TL and TR be t. L and t. R respectively. (t = t. L+ t. R) Height of TL and TR are both < k+1. TL TR By inductive hypothesis, t. L £ 2(TL Height) £ 2 k and t. R £ 2(TR Height) £ 2 k. t = t. L+ t. R £ 2 k + 2 k = 2 k+1. kavita hatwal math 231 fall 2002 k

• Corollary to the Leaves-Height Theorem: Let T=(V, E) be a binary tree that has t leaves, and height h. Then log 2 t £ h. Proof: Using leaves-height theorem, we have t £ 2 h. Taking logarithms on both sides will yield log 2 t £ log 22 h log 2 t £ h kavita hatwal math 231 fall 2002

Examples • Q: Is there a binary tree that has height 5 and 38 external vertices? • A: No, since 38 > 25 which violates the leaves-height theorem. kavita hatwal math 231 fall 2002

Examples • Q: Is there a full binary tree with 10 internal vertices and 13 external vertices? • A: No. Using the full-tree theorem, a binary tree with 10 internal vertices has 21 vertices in total. Therefore there should be 21 -10 = 11 external vertices. kavita hatwal math 231 fall 2002

Leaves-Height Theorem. IN GENERAL: • Leaves-Height Theorem for m-ary Trees: Let T=(V, E) be a m-ary tree that has t leaves, and height h. Then t £ mh • Corollary to the Leaves-Height Theorem: Let T=(V, E) be a m-ary tree that has t leaves, and height h. Then logmt £ h kavita hatwal math 231 fall 2002

Spanning Trees • A spanning tree T of a graph G is a subgraph of G that contains every vertex of G and is a tree. kavita hatwal math 231 fall 2002

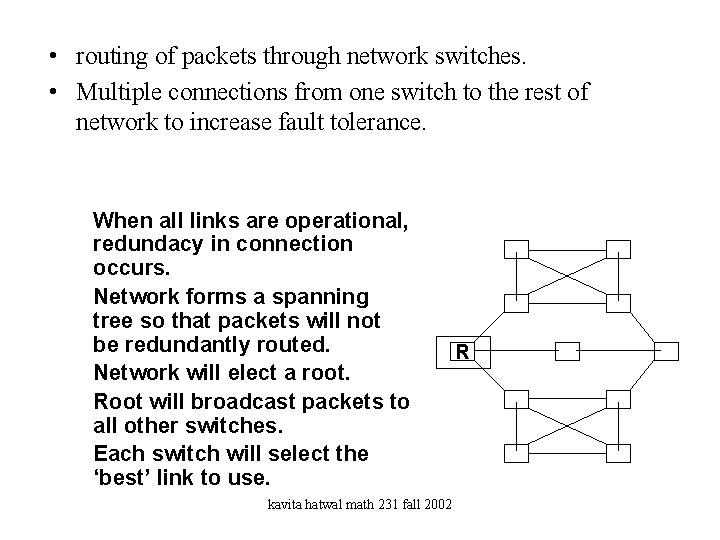
• routing of packets through network switches. • Multiple connections from one switch to the rest of network to increase fault tolerance. n n n When all links are operational, redundacy in connection occurs. Network forms a spanning tree so that packets will not be redundantly routed. Network will elect a root. Root will broadcast packets to all other switches. Each switch will select the ‘best’ link to use. kavita hatwal math 231 fall 2002 R

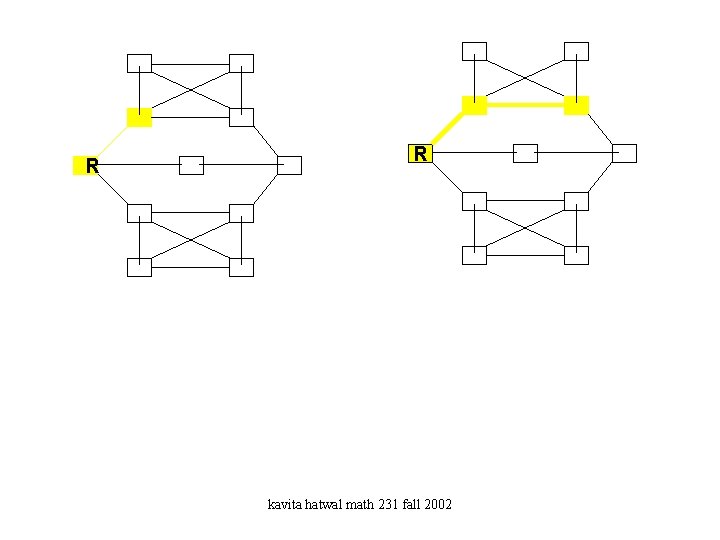
R R kavita hatwal math 231 fall 2002

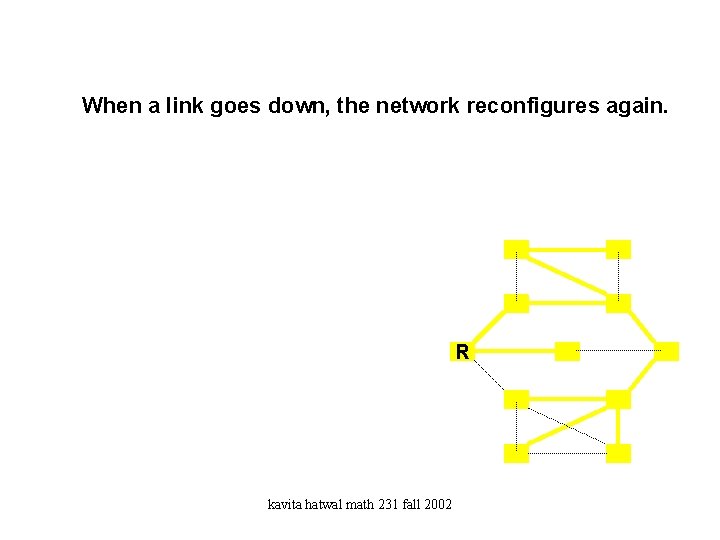
n When a link goes down, the network reconfigures again. R kavita hatwal math 231 fall 2002

Spanning Trees • Theorem: Every connected graph has a spanning tree. • Proof: – If the graph contains circuits, then remove, one by one, edges that break the circuits until there are no more circuits. – The resulting subgraph is a tree. kavita hatwal math 231 fall 2002

Weighted Graphs • A weighted graph G is a triple (V, E, w) where V and E are the vertices and edges and w is a function w : E R. • For each edge e, the value w(e) is called the weight of the edge. • In applications, often the weights represent a cost of some sort. kavita hatwal math 231 fall 2002

Examples: Weighted Graphs • A highway map. – The cities are the vertices. – The highways are the edges. – The distances are the weights. • A computer network. – The hardware units are the vertices. – The communication lines are the edges. – The cost of installing the lines are the weights. kavita hatwal math 231 fall 2002

Minimal Spanning Trees • Since the weights often represent a cost of some sort, a goal often is to minimize the total weight of a graph. kavita hatwal math 231 fall 2002

Kruskal’s Algorithm • Let G be a connected weighted graph with n vertices. • Initialize T to have all the vertices of G, but no edges. • Let m = 0. kavita hatwal math 231 fall 2002

Kruskal’s Algorithm • While (m < n – 1) – Find an edge e in E of least weight. – Delete e from E. – If the addition of e to the edges of T does not create a circuit, then • Add e to E(T). • Increment m. kavita hatwal math 231 fall 2002

Kruskal’s Algorithm • When the while loop ends, T is a minimal spanning tree of G. kavita hatwal math 231 fall 2002

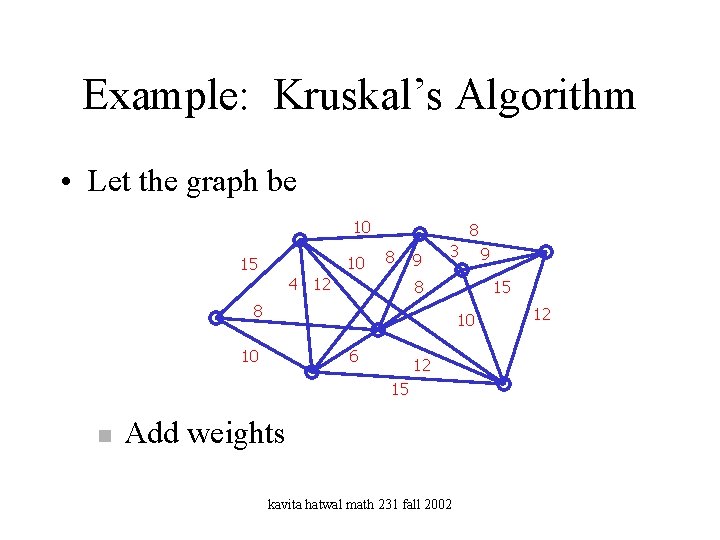
Example: Kruskal’s Algorithm • Let the graph be 10 10 15 8 8 4 12 9 3 8 8 6 12 15 n 15 10 10 Add weights kavita hatwal math 231 fall 2002 9 12

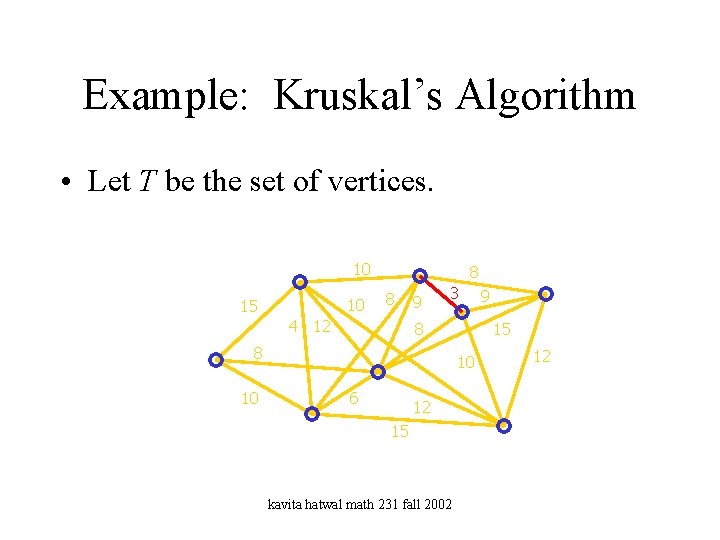
Example: Kruskal’s Algorithm • Let T be the set of vertices. 10 10 15 8 8 4 12 9 3 8 8 10 15 10 6 12 15 kavita hatwal math 231 fall 2002 9 12

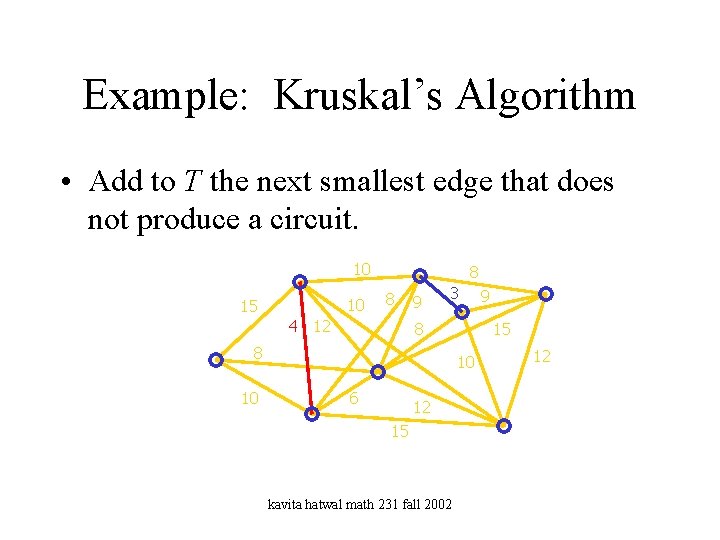
Example: Kruskal’s Algorithm • Add to T the next smallest edge that does not produce a circuit. 10 10 15 8 8 4 12 9 3 8 8 10 15 10 6 12 15 kavita hatwal math 231 fall 2002 9 12

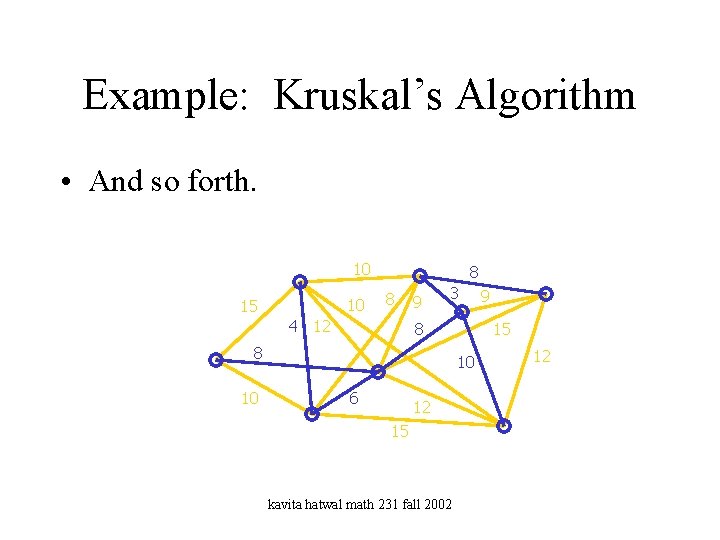
Example: Kruskal’s Algorithm • And so forth. 10 10 15 8 8 4 12 9 3 8 8 10 15 10 6 12 15 kavita hatwal math 231 fall 2002 9 12

Prim’s Algorithm • Let G be a connected weighted graph. • Choose a vertex v of G and let T be a graph consisting of only that one vertex. • Let V be all the vertices of G except v. kavita hatwal math 231 fall 2002

Prim’s Algorithm • For i = 1 to n – 1 – Find an edge e of G such that • e connects T to a vertex in V, and • e has the least weight of all edges connecting T to a vertex in V. – Add that vertex to T and delete it from V. kavita hatwal math 231 fall 2002

Prim’s Algorithm • When the for loop ends, T is a minimal spanning tree of G. kavita hatwal math 231 fall 2002

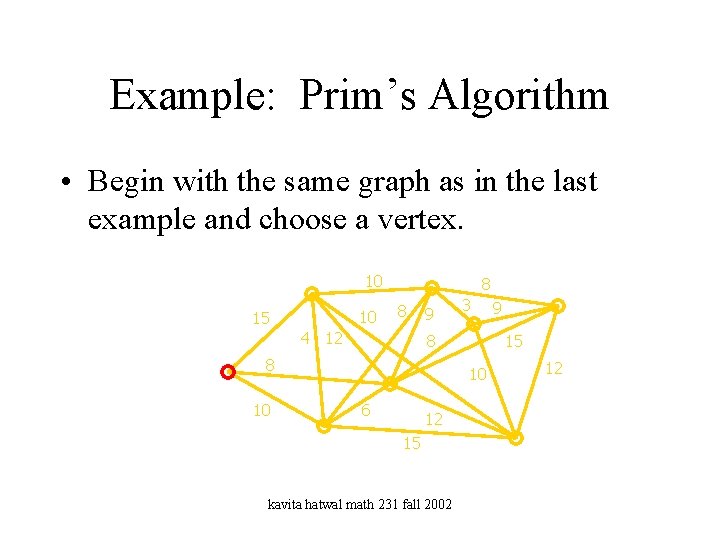
Example: Prim’s Algorithm • Begin with the same graph as in the last example and choose a vertex. 10 10 15 8 8 4 12 9 8 8 10 3 15 10 6 12 15 kavita hatwal math 231 fall 2002 9 12

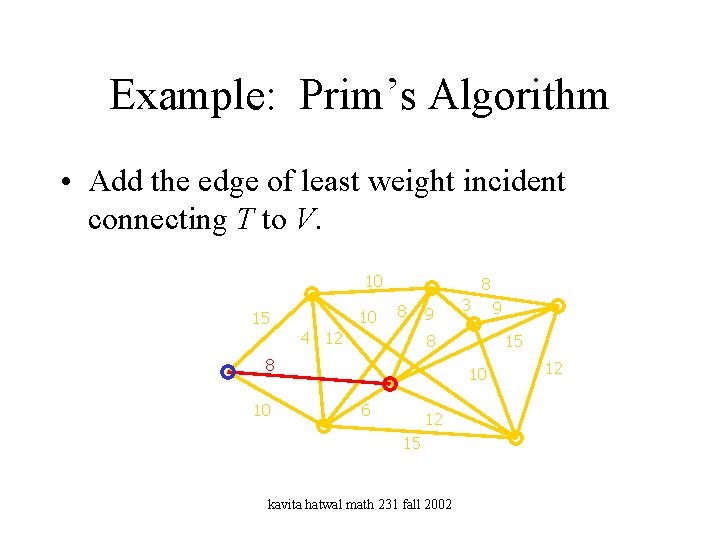
Example: Prim’s Algorithm • Add the edge of least weight incident connecting T to V. 10 10 15 8 8 4 12 9 8 8 10 3 15 10 6 12 15 kavita hatwal math 231 fall 2002 9 12

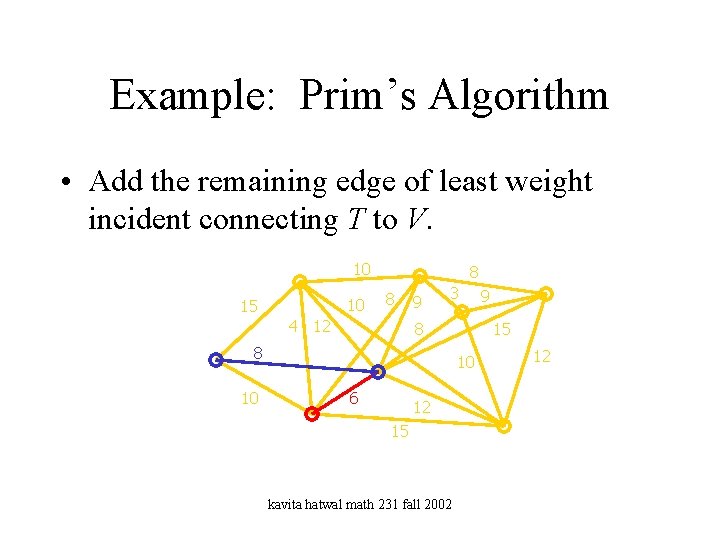
Example: Prim’s Algorithm • Add the remaining edge of least weight incident connecting T to V. 10 10 15 8 8 4 12 9 3 8 8 10 15 10 6 12 15 kavita hatwal math 231 fall 2002 9 12

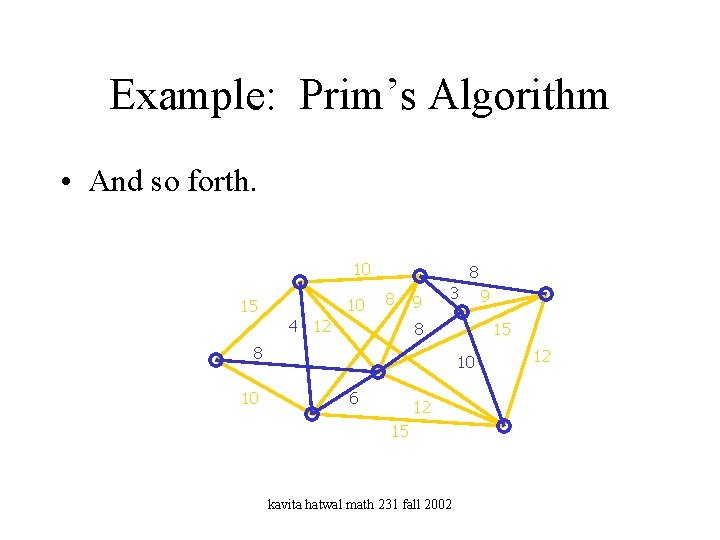
Example: Prim’s Algorithm • And so forth. 10 10 15 8 8 4 12 9 3 8 8 10 15 10 6 12 15 kavita hatwal math 231 fall 2002 9 12

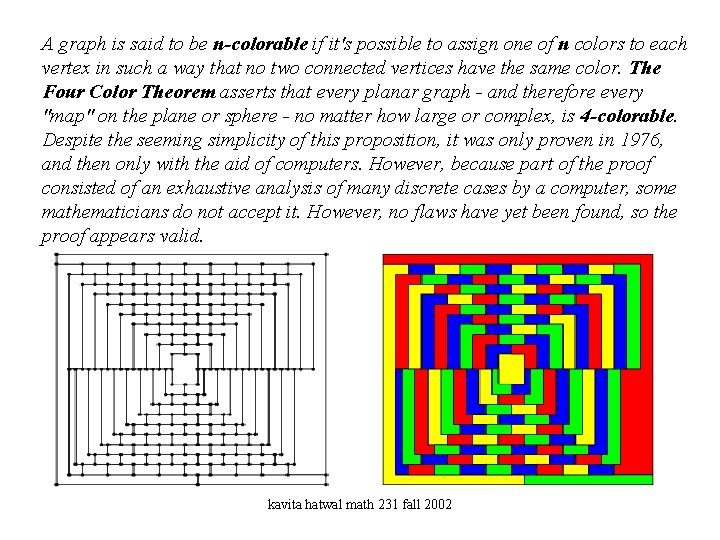
A graph is said to be n-colorable if it's possible to assign one of n colors to each vertex in such a way that no two connected vertices have the same color. The Four Color Theorem asserts that every planar graph - and therefore every "map" on the plane or sphere - no matter how large or complex, is 4 -colorable. Despite the seeming simplicity of this proposition, it was only proven in 1976, and then only with the aid of computers. However, because part of the proof consisted of an exhaustive analysis of many discrete cases by a computer, some mathematicians do not accept it. However, no flaws have yet been found, so the proof appears valid. kavita hatwal math 231 fall 2002

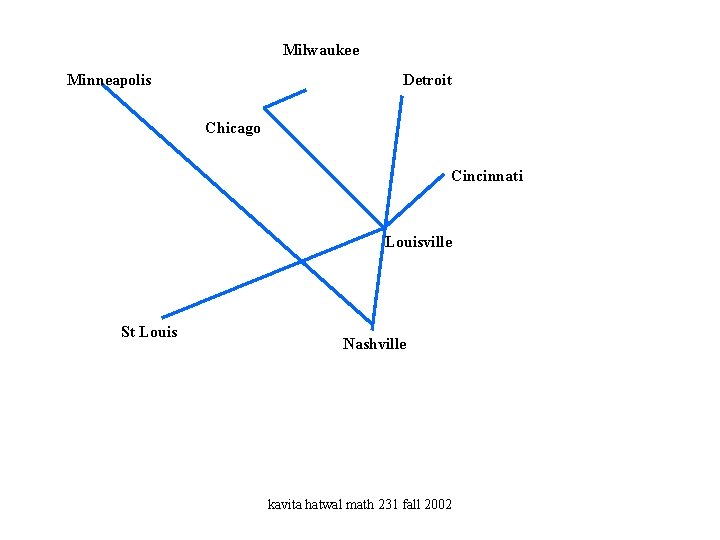
Spanning trees algorithms Milwaukee Minneapolis Detroit Chicago Louisville St Louis Nashville kavita hatwal math 231 fall 2002

Milwaukee Minneapolis Detroit Chicago Cincinnati Louisville St Louis Nashville kavita hatwal math 231 fall 2002

A spanning tree for a graph G is a subgraph of G that contains every vertex of G and is a tree. • Every connected graph has a spanning tree. • Any 2 spanning trees for a graph have the same number of edges. Page 684, example 11. 6. 1 kavita hatwal math 231 fall 2002

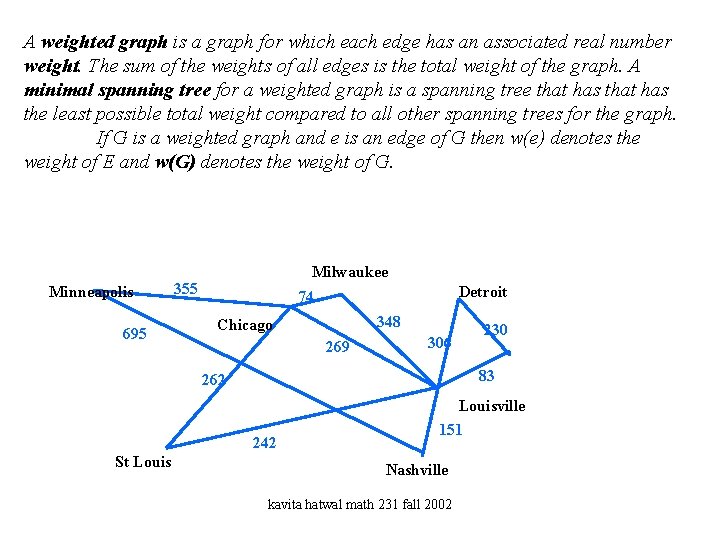
A weighted graph is a graph for which each edge has an associated real number weight. The sum of the weights of all edges is the total weight of the graph. A minimal spanning tree for a weighted graph is a spanning tree that has the least possible total weight compared to all other spanning trees for the graph. If G is a weighted graph and e is an edge of G then w(e) denotes the weight of E and w(G) denotes the weight of G. Minneapolis 695 Milwaukee 355 Detroit 74 348 Chicago 269 230 306 83 262 Louisville 242 St Louis 151 Nashville kavita hatwal math 231 fall 2002

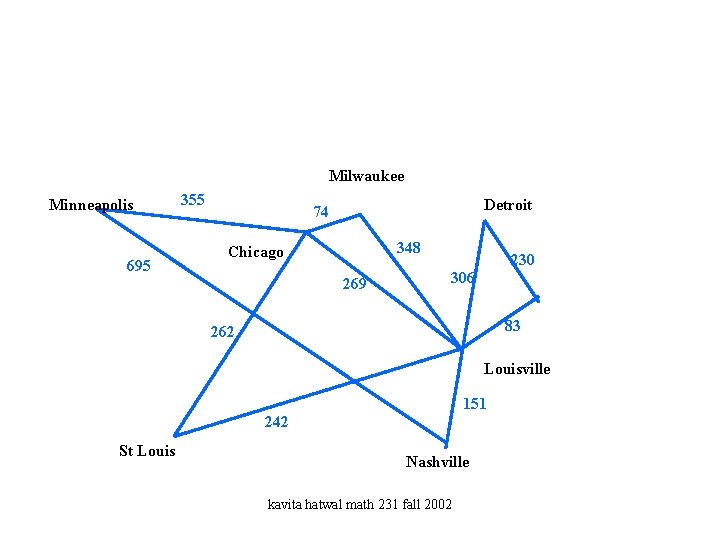
Milwaukee Minneapolis 695 355 Detroit 74 348 Chicago 269 230 306 83 262 Louisville 151 242 St Louis Nashville kavita hatwal math 231 fall 2002

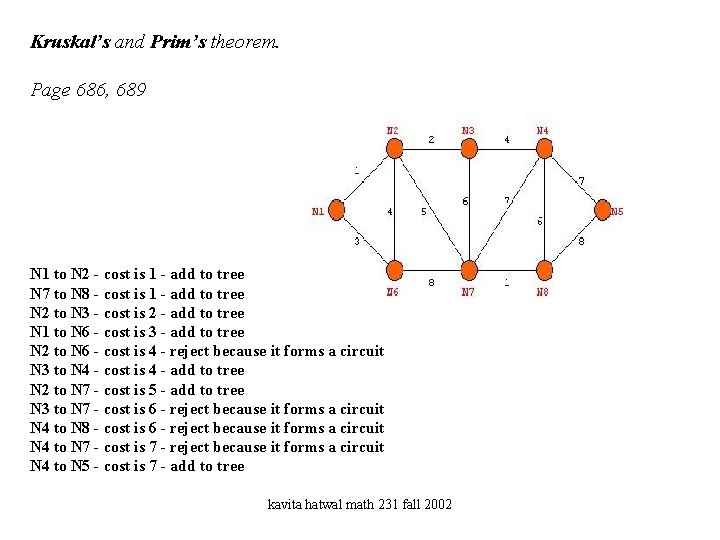
Kruskal’s and Prim’s theorem. Page 686, 689 N 1 to N 2 - cost is 1 - add to tree N 7 to N 8 - cost is 1 - add to tree N 2 to N 3 - cost is 2 - add to tree N 1 to N 6 - cost is 3 - add to tree N 2 to N 6 - cost is 4 - reject because it forms a circuit N 3 to N 4 - cost is 4 - add to tree N 2 to N 7 - cost is 5 - add to tree N 3 to N 7 - cost is 6 - reject because it forms a circuit N 4 to N 8 - cost is 6 - reject because it forms a circuit N 4 to N 7 - cost is 7 - reject because it forms a circuit N 4 to N 5 - cost is 7 - add to tree kavita hatwal math 231 fall 2002
 Non finite subordinate clause
Non finite subordinate clause What is finite verb
What is finite verb Learning objectives of non finite verbs
Learning objectives of non finite verbs Finite and nonfinite verbs
Finite and nonfinite verbs Finite and non finite
Finite and non finite Total set awareness set consideration set
Total set awareness set consideration set Training set validation set test set
Training set validation set test set Finite set example
Finite set example Handshaking theorem
Handshaking theorem Game theory and graph theory
Game theory and graph theory Bounded set vs centered set
Bounded set vs centered set Crisp set vs fuzzy set
Crisp set vs fuzzy set Crisp set vs fuzzy set
Crisp set vs fuzzy set Crisp set vs fuzzy set
Crisp set vs fuzzy set What is the overlap of data set 1 and data set 2?
What is the overlap of data set 1 and data set 2? Surjective vs injective
Surjective vs injective Maximum size of independent set is
Maximum size of independent set is What is an independent set in a graph
What is an independent set in a graph Graph set up
Graph set up Konsep dasar logika himpunan
Konsep dasar logika himpunan Set theory
Set theory Proper subset symbol
Proper subset symbol Absorption law
Absorption law Set theory in dbms
Set theory in dbms Set theory
Set theory Set theory identities
Set theory identities Set theory practice
Set theory practice Laws of set theory in discrete mathematics
Laws of set theory in discrete mathematics Dilworth theorem
Dilworth theorem Set theory operators
Set theory operators Rough set theory
Rough set theory Set theory
Set theory Cardinal number of a set
Cardinal number of a set Set theory
Set theory Basic concepts of set theory
Basic concepts of set theory 10-2 practice arithmetic sequences and series answer key
10-2 practice arithmetic sequences and series answer key Tcp segment header size
Tcp segment header size Summation notation
Summation notation Contoh soal fsa dan jawabannya
Contoh soal fsa dan jawabannya Automata
Automata Electric field of a finite line charge
Electric field of a finite line charge Sum of a finite arithmetic series
Sum of a finite arithmetic series Cochran formula for finite population
Cochran formula for finite population Waiting line analysis
Waiting line analysis Finite power series
Finite power series Finite state machine sequential circuits
Finite state machine sequential circuits Impartirea fractiilor zecimale exercitii
Impartirea fractiilor zecimale exercitii Limitations of finite state machine
Limitations of finite state machine Arithmetic sequence sigma notation
Arithmetic sequence sigma notation The canonical form
The canonical form Finite divided difference
Finite divided difference Nfa non deterministic finite automata
Nfa non deterministic finite automata Tipuri de elemente finite
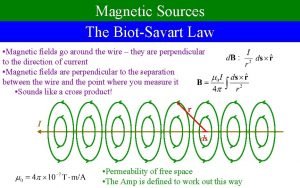
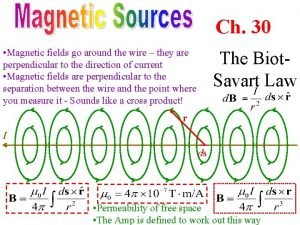
Tipuri de elemente finite Magnetic field of a finite wire
Magnetic field of a finite wire Finite verb latin
Finite verb latin Finite state machine with datapath
Finite state machine with datapath Finite state machine minimization
Finite state machine minimization Finite state automata (fsa) adalah
Finite state automata (fsa) adalah Potential energy well
Potential energy well What is finite loading
What is finite loading Finite differences
Finite differences Finite difference equation
Finite difference equation What are the advantages to finite capacity scheduling?
What are the advantages to finite capacity scheduling? Electric field of a finite line charge
Electric field of a finite line charge Vhdl finite state machine
Vhdl finite state machine Sample complexity for finite hypothesis spaces
Sample complexity for finite hypothesis spaces Traffic light finite state machine
Traffic light finite state machine Tcp connection management finite state machine
Tcp connection management finite state machine Finite potential well
Finite potential well Unordered subsets
Unordered subsets Time dependent schrodinger wave equation
Time dependent schrodinger wave equation Gerund examples
Gerund examples Finite divided difference
Finite divided difference Magnetic field of a finite wire
Magnetic field of a finite wire Cell line vs cell strain
Cell line vs cell strain Finite and continuous cell lines
Finite and continuous cell lines Finite and continuous cell lines
Finite and continuous cell lines Finite fields in cryptography
Finite fields in cryptography Infinite geometric series formula
Infinite geometric series formula Lexical analysis finite automata
Lexical analysis finite automata Geometric series sum
Geometric series sum Exponential data set examples
Exponential data set examples Finite element method example
Finite element method example Finite state diagram generator
Finite state diagram generator Finite linear game
Finite linear game Fsm vhdl
Fsm vhdl Elevator finite state machine
Elevator finite state machine Finite state automata didefinisikan dengan?
Finite state automata didefinisikan dengan? Finite probability space
Finite probability space Hourglass modes finite element method
Hourglass modes finite element method Automata
Automata The matrix cst
The matrix cst Finite state machine vending machine example
Finite state machine vending machine example Steadystate error
Steadystate error Truss finite element analysis
Truss finite element analysis Kevin conroy finite
Kevin conroy finite Newtons
Newtons Finite and infinite sets
Finite and infinite sets Kleenes theorem
Kleenes theorem Finite clauses
Finite clauses Nonessential adjective clause
Nonessential adjective clause Finite state machine
Finite state machine Finite fields in cryptography and network security
Finite fields in cryptography and network security Image preprocessing
Image preprocessing Ospf finite state machine
Ospf finite state machine Energy of signal
Energy of signal Finite state machine
Finite state machine Finite defination
Finite defination Finite state machine game
Finite state machine game One sided limits
One sided limits Zimbio
Zimbio Dfa stands for in automata
Dfa stands for in automata Wwwpom
Wwwpom State diagram
State diagram Equivalent formulas
Equivalent formulas Cherenkov radiation formula
Cherenkov radiation formula Finite differences polynomials
Finite differences polynomials Finite element
Finite element Output berasosiasi dengan state adalah untuk
Output berasosiasi dengan state adalah untuk Finite difference time domain
Finite difference time domain Finite element analysis
Finite element analysis Phases of finite element method
Phases of finite element method What is impedance
What is impedance Finite impulse response
Finite impulse response Finite word length
Finite word length Finite risk insurance
Finite risk insurance Fem geotechnics
Fem geotechnics Finite elements method
Finite elements method Finite difference time domain
Finite difference time domain Deterministic finite automaton
Deterministic finite automaton