Deterministic Finite Automata Nondeterministic Finite Automata Deterministic Finite

Deterministic Finite Automata Nondeterministic Finite Automata

Deterministic Finite Automata n n n A regular expression can be represented (and recognized) by a machine called a deterministic finite automaton (dfa). A dfa can then be used to generate the matrix (or table) used by the scanner (or lexical analyzer). Deterministic finite automata are frequently also called simply finite automata (fa).

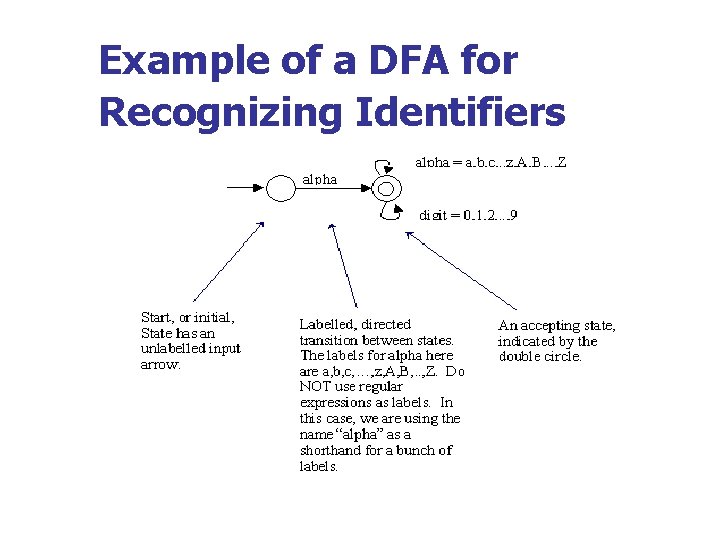
Example of a DFA for Recognizing Identifiers

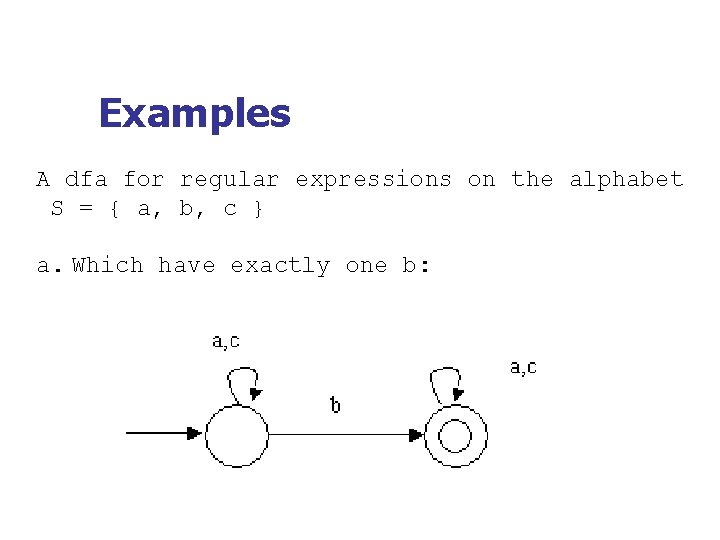
Examples A dfa for regular expressions on the alphabet S = { a, b, c } a. Which have exactly one b:

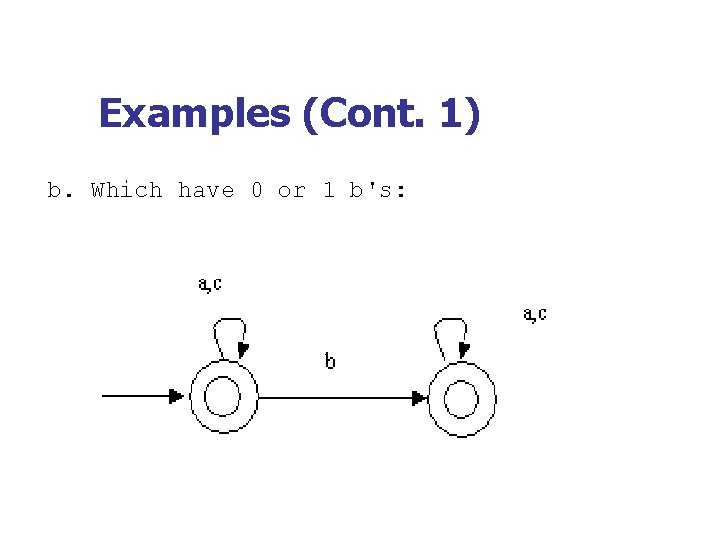
Examples (Cont. 1) b. Which have 0 or 1 b's:

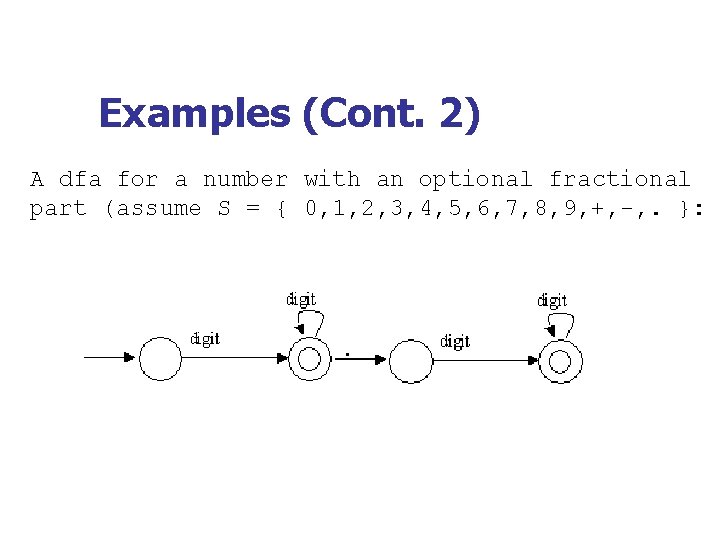
Examples (Cont. 2) A dfa for a number with an optional fractional part (assume S = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +, -, . }:

Constructing DFA n n n Regular expressions give us rules for recognizing the symbols or tokens of a programming language. The way a lexical analyzer can recognize the symbols is to use a DFA (machine) to construct a matrix, or table, that reports when a particular kind of symbol has been recognized. In order to recognize symbols, we need to know how to (efficiently) construct a DFA from a regular expression.

How to Construct a DFA from a Regular Expression n Construct a nondeterministic finite automata (nfa) Using the nfa, construct a dfa Minimize the number of states in the dfa to get a smaller dfa

Nondeterministic Finite Automata n n n A nondeterministic finite automata (NFA) allows transitions on a symbol from one state to possibly more than one other state. Allows -transitions from one state to another whereby we can move from the first state to the second without inputting the next character. In a NFA, a string is matched if there is any path from the start state to an accepting state using that string.

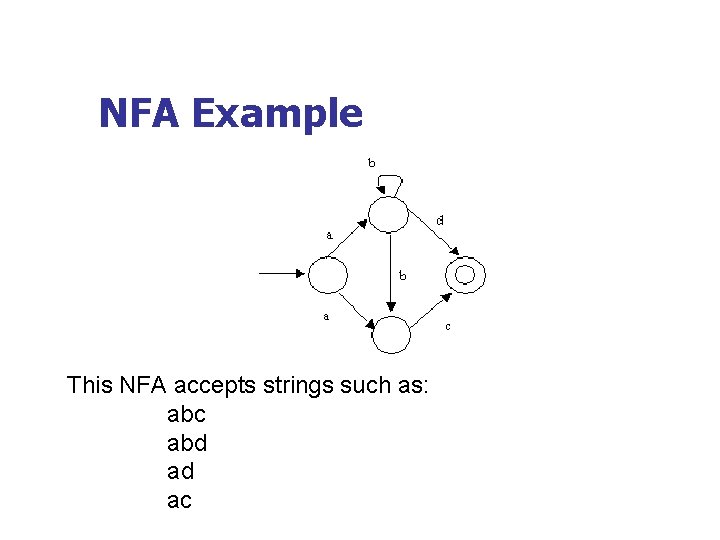
NFA Example This NFA accepts strings such as: abc abd ad ac

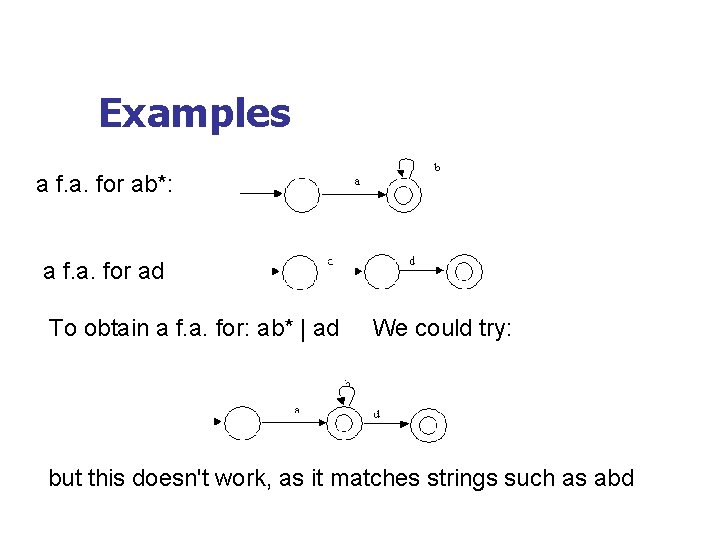
Examples a f. a. for ab*: a f. a. for ad To obtain a f. a. for: ab* | ad We could try: but this doesn't work, as it matches strings such as abd

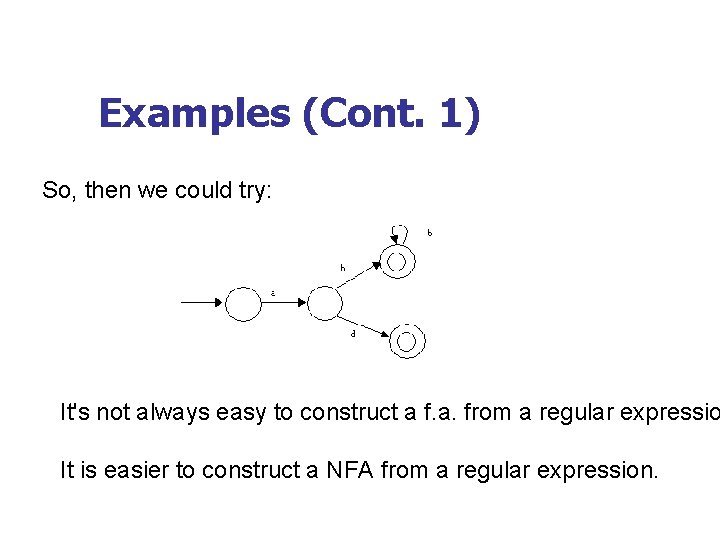
Examples (Cont. 1) So, then we could try: It's not always easy to construct a f. a. from a regular expressio It is easier to construct a NFA from a regular expression.

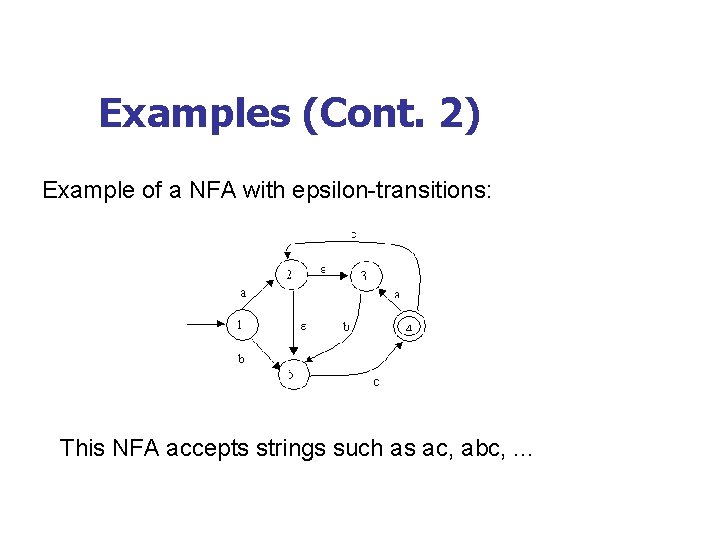
Examples (Cont. 2) Example of a NFA with epsilon-transitions: This NFA accepts strings such as ac, abc, . . .

Conventional Definition of Regular Expressions (RE) on some finite alphabet 1. 2. 3. 4. a. b. c. The empty set is an RE. The empty string is an RE. Any member of the alphabet is an RE. If R 1 and R 2 are Re’s, then so are: R 1 R 2 (concatenation) R 1 | R 2 (alternation) R 1* (closure)

Lex vs the conventional definition of a RE Lex’s definition of a RE includes the conventional definition, but in addition, provides additional basic RE’s. These however can be defined in terms of the conventional definition. For example: [c-e] can be expressed as c | d | e If R is a RE, then: R? can be expressed as R | ε R+ can be expressed as RR*

How to construct a NFA for any regular expression - 1 Basic building blocks: (1) Any letter a of the alphabet is recognized by: (2) The empty set Æ is recognized by:

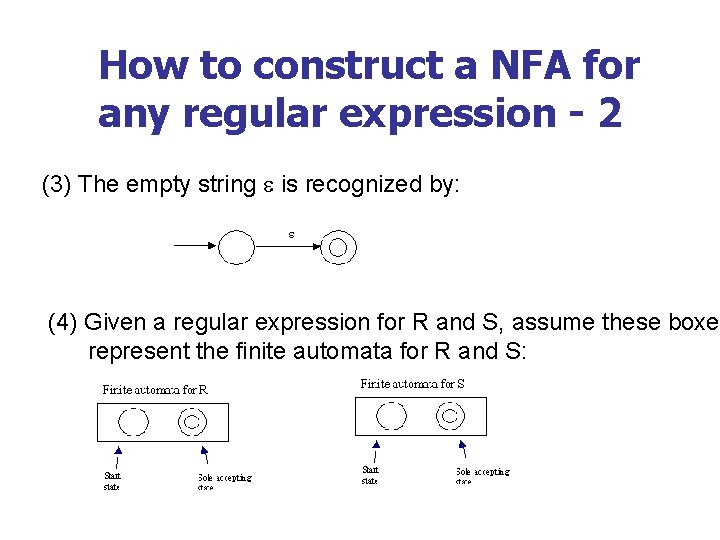
How to construct a NFA for any regular expression - 2 (3) The empty string is recognized by: (4) Given a regular expression for R and S, assume these boxes represent the finite automata for R and S:

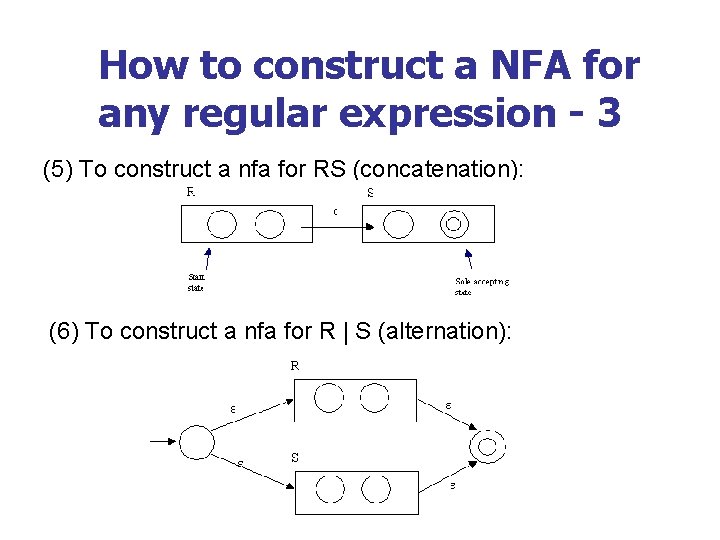
How to construct a NFA for any regular expression - 3 (5) To construct a nfa for RS (concatenation): (6) To construct a nfa for R | S (alternation):

How to construct a NFA for any regular expression - 4 (7) To construct a nfa for R* (closure):

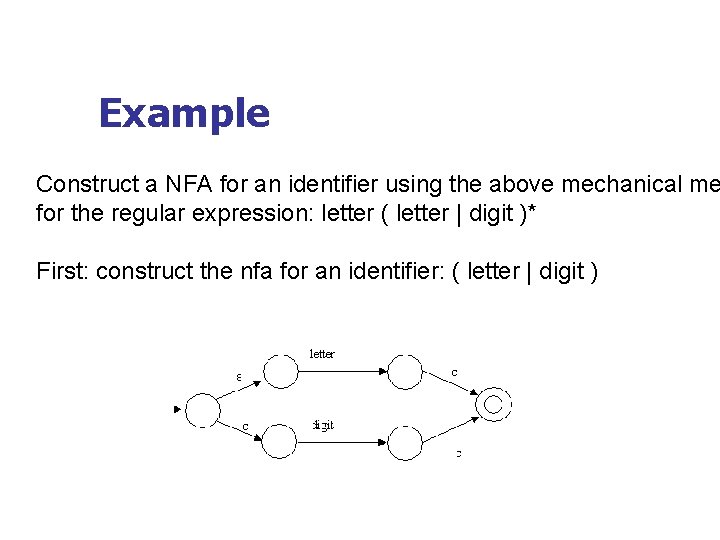
Example Construct a NFA for an identifier using the above mechanical me for the regular expression: letter ( letter | digit )* First: construct the nfa for an identifier: ( letter | digit )

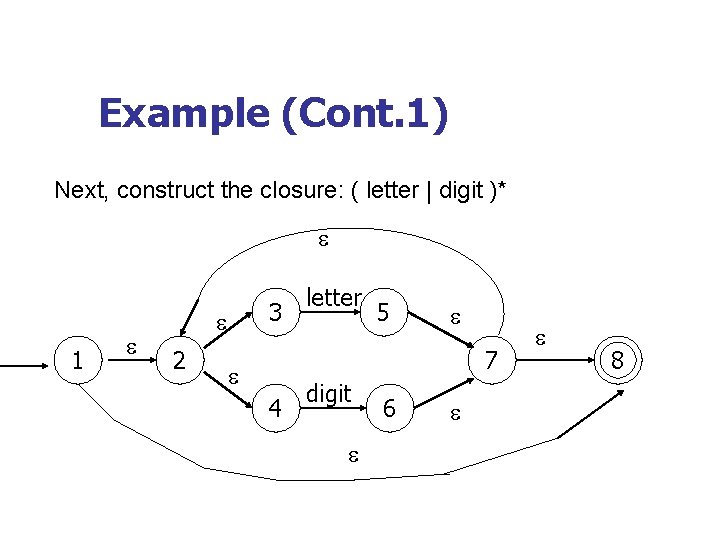
Example (Cont. 1) Next, construct the closure: ( letter | digit )* 1 3 2 letter 5 7 4 digit 6 8

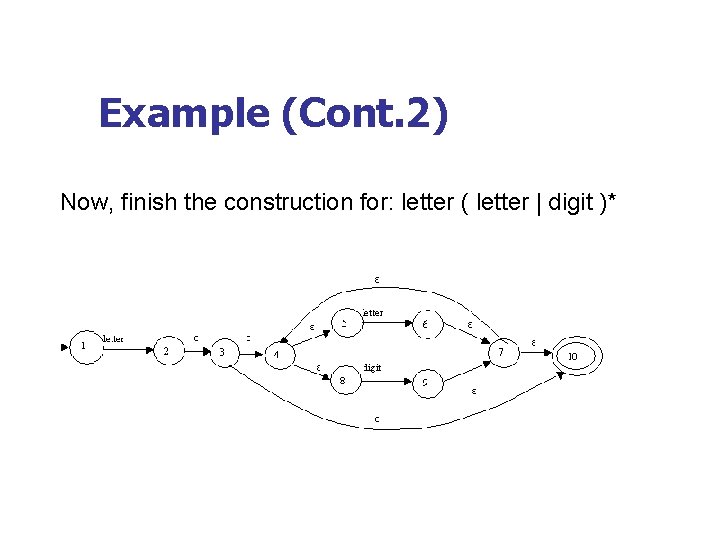
Example (Cont. 2) Now, finish the construction for: letter ( letter | digit )*