Examples for Finite Automata CSC 3130 Tutorial One

Examples for Finite Automata CSC 3130 Tutorial One Bridge Zhao bridger. zhao@gmail. com Department of Computer Science & Engineering

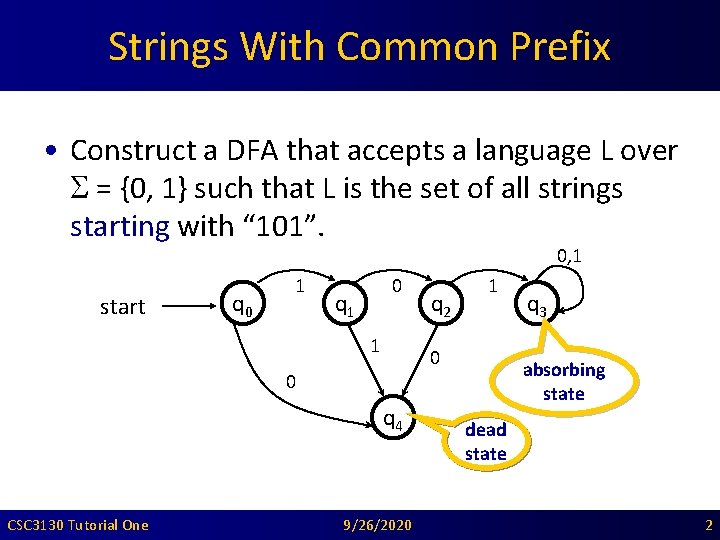
Strings With Common Prefix • Construct a DFA that accepts a language L over = {0, 1} such that L is the set of all strings starting with “ 101”. 0, 1 start q 0 1 0 q 1 1 0 0 q 4 CSC 3130 Tutorial One q 2 1 9/26/2020 q 3 absorbing state dead state 2

Strings With Common Suffix • Construct a DFA that accepts a language L over = {0, 1} such that L is the set of all strings ending with “ 101”. 0 0 start q 0 1 1 q 1 0 q 2 0 1 q 3 1 CSC 3130 Tutorial One 9/26/2020 3

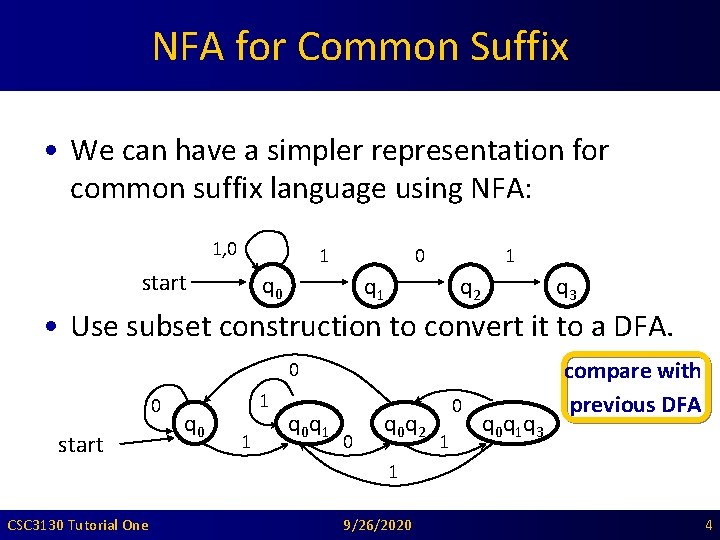
NFA for Common Suffix • We can have a simpler representation for common suffix language using NFA: 1, 0 1 start 0 q 0 1 q 2 q 3 • Use subset construction to convert it to a DFA. 0 0 start q 0 1 1 q 0 q 1 0 q 2 0 1 q 0 q 1 q 3 compare with previous DFA 1 CSC 3130 Tutorial One 9/26/2020 4

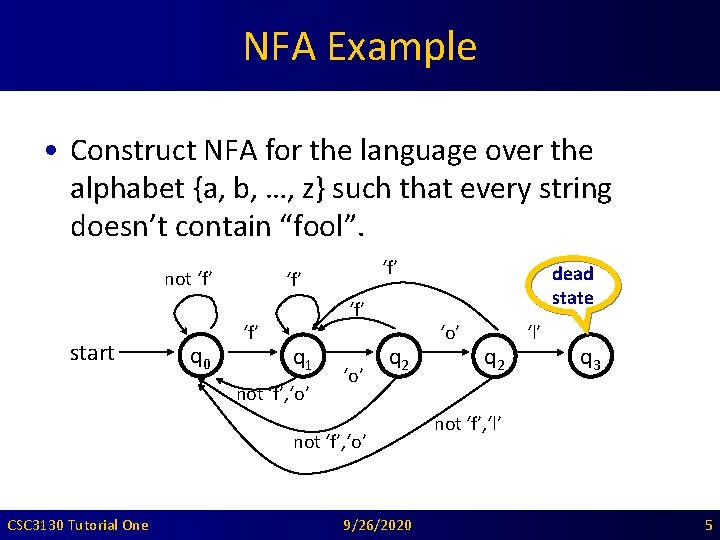
NFA Example • Construct NFA for the language over the alphabet {a, b, …, z} such that every string doesn’t contain “fool”. not ‘f’ start q 0 ‘f’ ‘f’ q 1 not ‘f’, ‘o’ q 2 not ‘f’, ‘o’ CSC 3130 Tutorial One 9/26/2020 dead state ‘o’ q 2 ‘l’ q 3 not ‘f’, ‘l’ 5

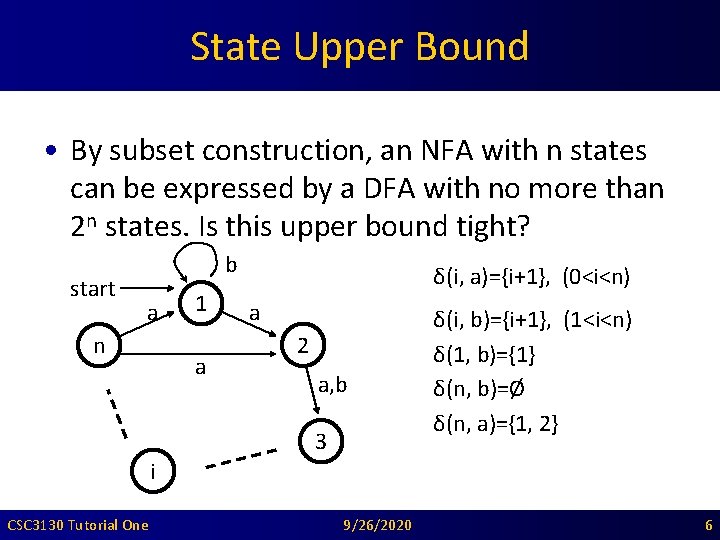
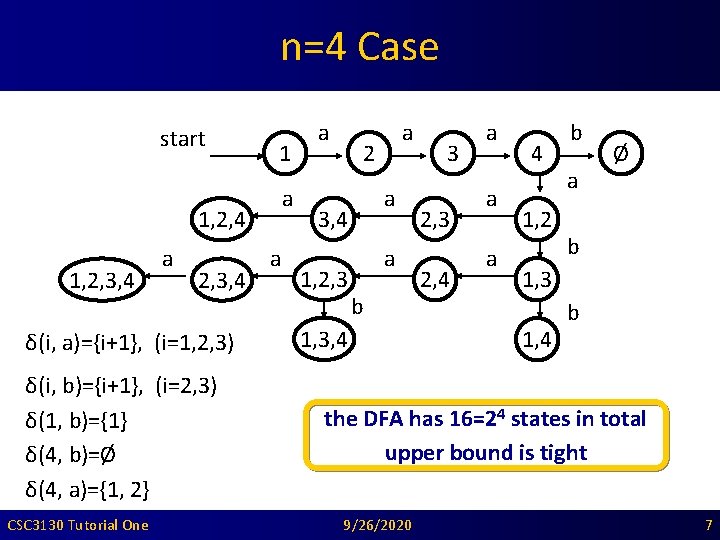
State Upper Bound • By subset construction, an NFA with n states can be expressed by a DFA with no more than 2 n states. Is this upper bound tight? start b a n 1 a δ(i, a)={i+1}, (0<i<n) a 2 a, b 3 δ(i, b)={i+1}, (1<i<n) δ(1, b)={1} δ(n, b)=Ø δ(n, a)={1, 2} i CSC 3130 Tutorial One 9/26/2020 6

n=4 Case start 1 a 1, 2, 4 1, 2, 3, 4 a 2, 3, 4 δ(i, a)={i+1}, (i=1, 2, 3) δ(i, b)={i+1}, (i=2, 3) δ(1, b)={1} δ(4, b)=Ø δ(4, a)={1, 2} CSC 3130 Tutorial One a a a 2 a 3, 4 1, 2, 3 a b 1, 3, 4 3 2, 4 a a a 4 1, 2 b a Ø b 1, 3 1, 4 b the DFA has 16=24 states in total upper bound is tight 9/26/2020 7

Regular Expressions • Construct a RE over d={0, 1} such that 1) It contains all strings that have two consecutive “ 0”s. 2) It contains all strings except those with two consecutive “ 0”s. 3) It contains all strings with an even number of “ 0”s. CSC 3130 Tutorial One 9/26/2020 8

Tips for RE Construction 1. (1+0)*00(1+0*) 2. We can divide the string into segments: 01110101111 (ε +0) (11*0)* 1* 3. Use similar idea as 2: ((1*0))*1* CSC 3130 Tutorial One 9/26/2020 9