Nondeterministic Finite Automata NFAs Reminder Deterministic Finite Automata

Nondeterministic Finite Automata (NFAs)

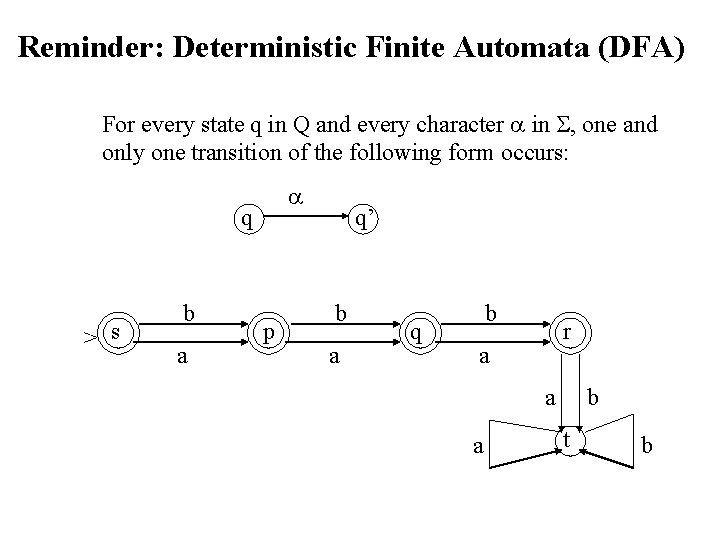
Reminder: Deterministic Finite Automata (DFA) For every state q in Q and every character in , one and only one transition of the following form occurs: q > s b a p q’ b a q b r a a a b t b

Expressiveness of DFA • DFA are a type of programs • Contains concepts of imperative languages: sequences, branching and loops. • Can implement a newspaper vendor machine or even control a character in a video game • Can implement pattern matching: find all text containing “Britney Spears” (or “Justin Timberlake”) • Can only implement programs that require a constant amount of memory

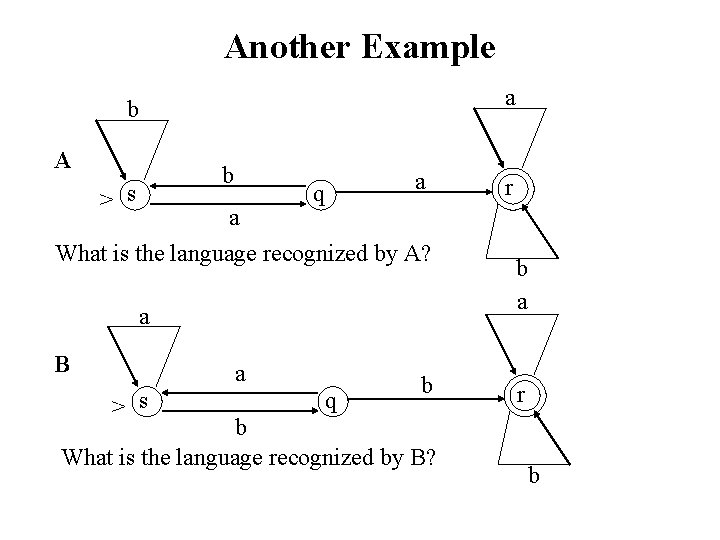
Another Example a b A b > s a q a What is the language recognized by A? a B a > s q b b What is the language recognized by B? r b a r b

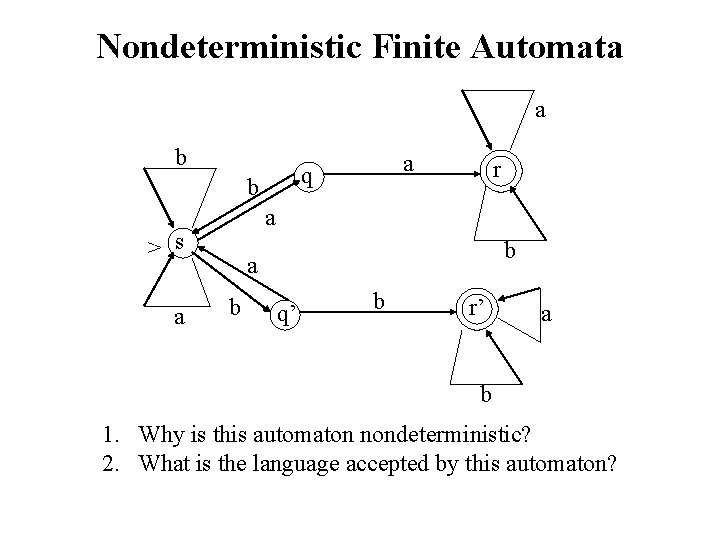
Nondeterministic Finite Automata a b b r a > s a a q b a b q q’ b r r’ a b 1. Why is this automaton nondeterministic? 2. What is the language accepted by this automaton?

Nondeterministic Finite Automata (NFA) For every state q in S and every character in , one of the following will happen: • No transition: q • One or more transitions: q occurs q’ … q’ p occurs

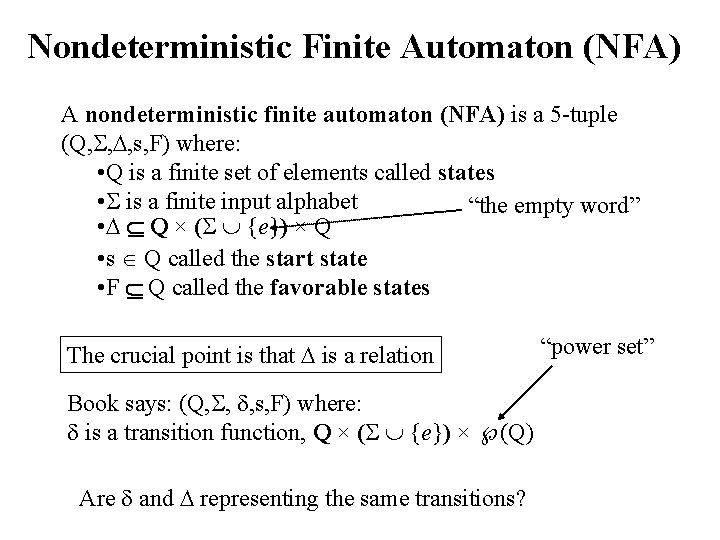
Nondeterministic Finite Automaton (NFA) A nondeterministic finite automaton (NFA) is a 5 -tuple (Q, , , s, F) where: • Q is a finite set of elements called states • is a finite input alphabet “the empty word” • Q × ( {e}) × Q • s Q called the start state • F Q called the favorable states The crucial point is that is a relation Book says: (Q, , , s, F) where: is a transition function, Q × ( {e}) × (Q) Are and representing the same transitions? “power set”

Nondeterministic Finite Automata (NFA) What else can occur in NFAs? q e q’ If next word to process in q is aaabbb and apply this transition, what is the word to be processed in q’? aaabbb “e-transitions” do not process any characters, they just allow to “jump” between states

Formal Definition of Computation for NFAs • Given a nodeterministic finite automaton N= (Q, , , s, F), and let w = w 1 w 2 …wn, where each wi is in M accepts w if we can write w as: w = y 1 y 2 …ym , where each yi is in ( {e}) and there is a sequence of states r 0 r 1, r 2 … rm in Q such that: 1. r 0 is the start state of M 2. ri+1 (ri , wi+1) for i = 0, …, m-1 3. rm F • Language recognized by N: {w in * : N accepts w}

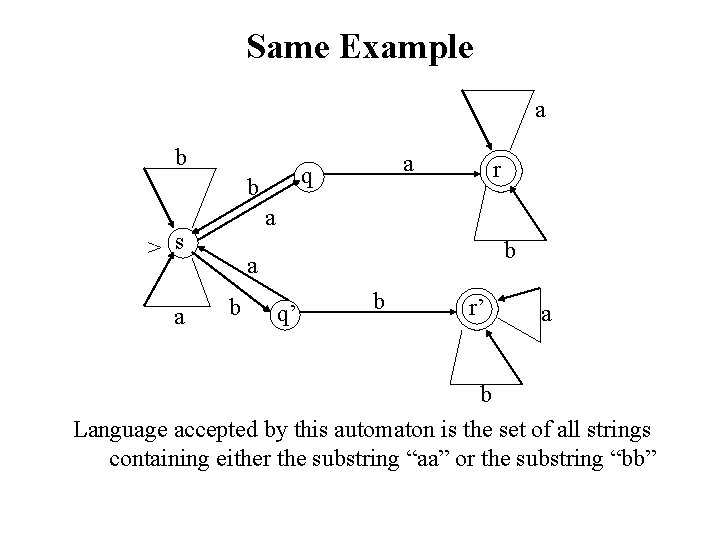
Same Example a b b r a > s a a q b a b q q’ b r r’ a b Language accepted by this automaton is the set of all strings containing either the substring “aa” or the substring “bb”

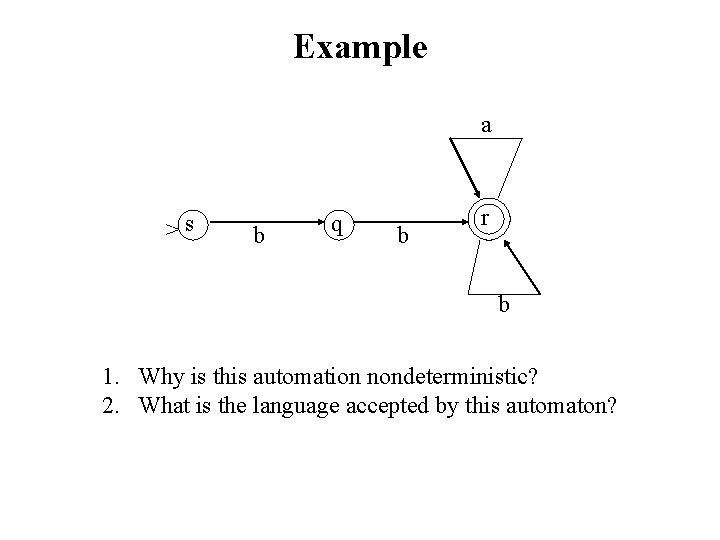
Example a >s b q b r b 1. Why is this automation nondeterministic? 2. What is the language accepted by this automaton?

Why We Study Nondeterministic Computation? • Makes it easier to prove properties about Automata – In particular, makes it easier to prove certain properties: • If A is a regular language then AR is also regular • It also makes it possible to understand the boundaries of computation – P = NP?

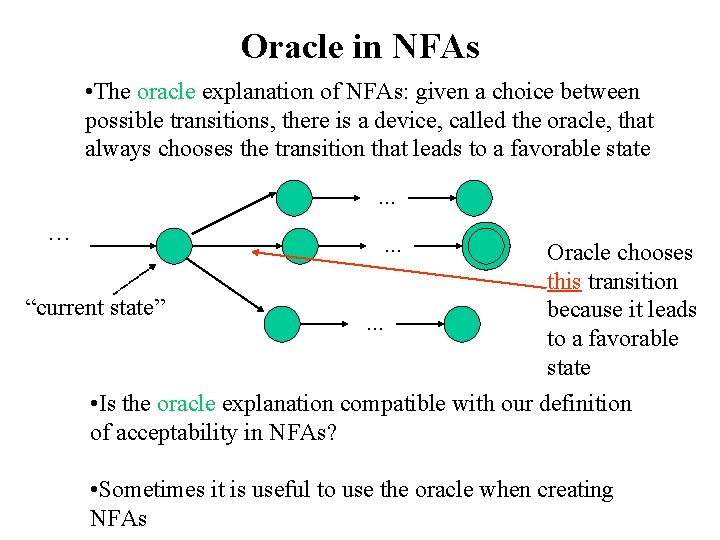
Oracle in NFAs • The oracle explanation of NFAs: given a choice between possible transitions, there is a device, called the oracle, that always chooses the transition that leads to a favorable state. . . … . . . Oracle chooses this transition “current state” because it leads. . . to a favorable state • Is the oracle explanation compatible with our definition of acceptability in NFAs? • Sometimes it is useful to use the oracle when creating NFAs

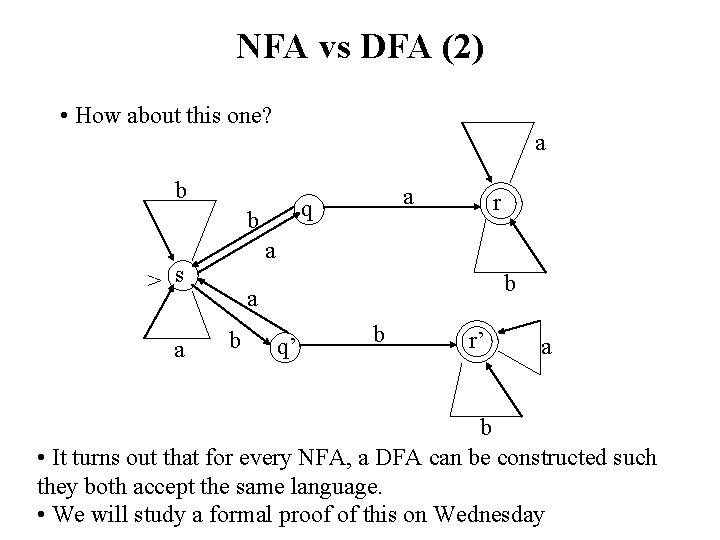
NFA vs DFA • Every DFA can be seen as an NFA • But not every NFA can be seen as a DFA • Are DFA’s more expressive? What does this means? It means that there an NFA can be constructed that accepts a language L for which no DFA can be constructed that accepts L • For example, is there an DFA that accepts the same language accepted by the following NFA? a >s b q b r b

NFA vs DFA (2) • How about this one? a b b r a > s a a q b a b q q’ b r r’ a b • It turns out that for every NFA, a DFA can be constructed such they both accept the same language. • We will study a formal proof of this on Wednesday