Objectives 1 Understand the difference between a finite

Objectives 1. Understand the difference between a finite and infinite series. 2. Write and evaluate an arithmetic series.

Understand the difference between Finite and Infinite Series: The sum of the terms of a sequence. Finite Sequences & Series: Can be counted and totaled (has an end). Infinite Sequences & Series: Cannot be counted and totaled (does not have an end). Finite Sequence Finite Series 6, 9, 12, 15, 18 6 + 9 + 12 + 15 + 18 Infinite Sequence Infinite Series 3, 7, 11, 15, . . . 3 + 7 + 11 + 15. . .

Example 1: Writing & Evaluating a Series Use the finite sequence 2, 11, 20, 29, 38, 47. Write the related series, and then evaluate. Related Series: 2 + 11 + 20 + 29 + 38 + 47 = 147 Example 1: Practice 1. 21, 18, 15, 12, 9, 6, 3 21 + 18 + 15 + 12 + 9 + 6 + 3; 84 2. 100, 99, 98, . . . , 95 100 + 99 + 98 + 97 + 96 + 95; 585 3. 17. 3, 19. 6, 21. 9, 24. 2, 26. 5 17. 3 + 19. 6 + 21. 9 + 24. 2 + 26. 5; 109. 5

Arithmetic Series A series whose terms form an arithmetic sequence. When a sequence has many terms, or when you know only the 1 st and last terms of the sequence, you can use a formula to evaluate the related series quickly. Sum of a Finite Arithmetic Series The sum Sn of a finite arithmetic series a 1 + a 2 + a 3 +. . . an is where a 1 is the 1 st term, an is the nth term, & n is the # of terms.

Example 2: Evaluating an Arithmetic Series Use the formula to evaluate the series related to the following sequence: 5, 7, 9, 11, 13 = 5 (5 + 13) 2 = 2. 5(18) = 45

Example 2: Practice Each sequence has 8 terms. Evaluate each related series. 4. 5. 5, 13, 21, . . . , 61 32 264 6. 1, 765, 1, 414, 1, 063, . . . , -692 4, 292

Objectives 1. Discover the sum of the terms of an arithmetic series. 2. Interpret summation notation and be able to rewrite as a series.

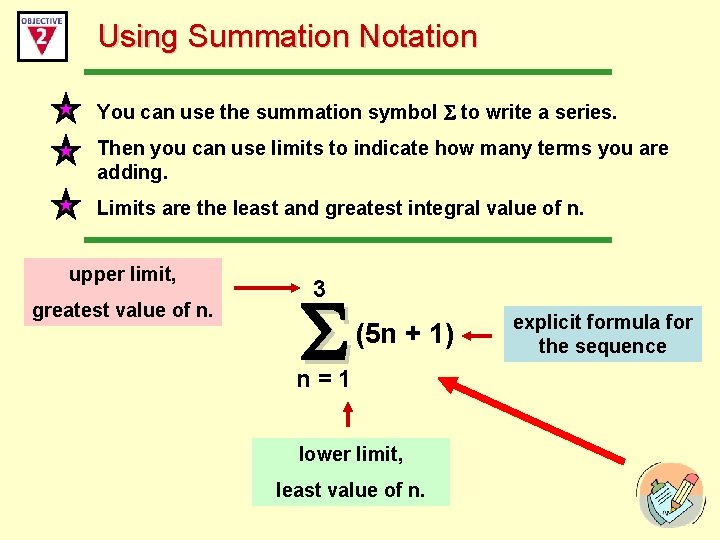
Using Summation Notation You can use the summation symbol to write a series. Then you can use limits to indicate how many terms you are adding. Limits are the least and greatest integral value of n. upper limit, greatest value of n. 3 (5 n + 1) n=1 lower limit, least value of n. explicit formula for the sequence

Example 3: Writing a Series in Summation Notation Use summation notation to write the series 3 + 6 + 9 +. . . for 33 items. 1 • 3=3 2 • 3=6 3 • 3=9 3 + 6 + 9 +. . . + 99 = The explicit formula for the 3 n sequence is ____. 33 3 n 1 The lower limit is ___. 1 33 The upper limit is ___.

Example 3: Practice Use summation notation to write each arithmetic series for the specified number of terms. 4 13. 2 + 4 + 6 +. . . ; n = 4 2 n n=1 7 15. 5 + 6 + 7 +. . . ; n = 7 17. 7 + 14 + 21 +. . . ; n = 15 (n + 4) n=1 15 7 n n=1

Example 4: Finding the Sum of a Series 3 Use the series (5 n + 1). n=1 a. Find the number of terms in the series. Since the values of n are 1, 2, & 3, there are ___ 3 terms. To expand a series from summation notation, substitute each value of n into the explicit formula and add the results. b. Find the first and last terms of the series. Term #1 = Term #3 = (5 n + 1) = 5(1) + 1 = 5(3) + 1 = 6 16 c. Evaluate the series. 3 (5 n + 1) n=1 = 5(1) + 1 + 5(2) + 1 + 5(3) + 1 = 6+ = 33 11 + 16

Example 4: Practice For each sum, find the number of terms, the first term, and the last term. Then evaluate the series. 5 19. (2 n - 1) n=1 5, 1, 9; 25 8 21. (7 - n) n=3 10 23. n=2 4 n 3 6, 4, -1; 9

Example 5: Real-World Application If Mary goes to the prom with Brian, he will be able to practice what he learned about sequences and series in Alg. 2 class. The price 4 hours of the of fun tickets 1 + 4 + 16 + 64 + 256. 1 date 16 cups of fruit punch How many times Bobby tried to ask her but chickened out. Questions 1. Is this series arithmetic, geometric, or neither? geometric 2. Kayla, will you go to the prom with Bobby? ?