Graph Theory Chapter 1 An Introduction to Graphs

Graph Theory Chapter 1 An Introduction to Graphs 大葉大學(Da-Yeh Univ. ) 資訊 程系(Dept. CSIE) 黃鈴玲(Lingling Huang)

Outline 1. 1 1. 2 1. 3 1. 4 1. 5 1. 6 1. 7 1. 8 1. 9 What is a graph? The Degree of a Vertex Isomorphic Graphs Subgraphs Degree Sequences Connected Graphs Cut-Vertices and Bridges Special graphs Digraphs Ch 1 -2 Copyright 黃鈴玲

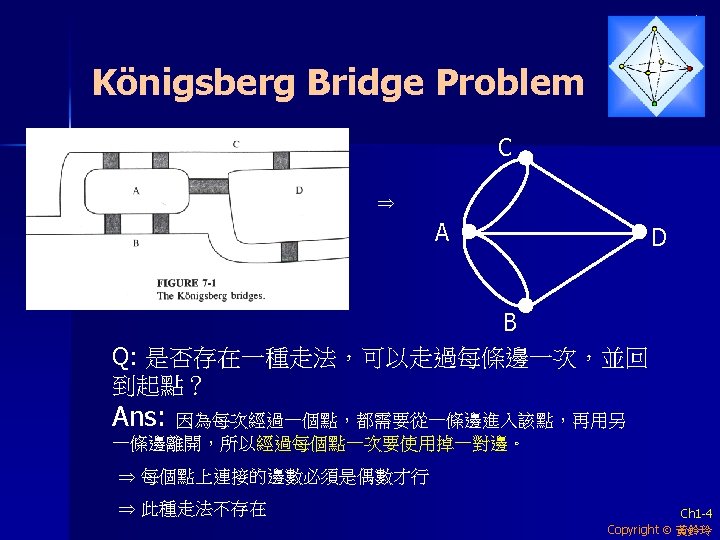
Graph Theory 的起源 n 1736, Euler solved the Königsberg Bridge Problem (七橋問題) Q: 是否存在一 種走法，可以走 過每座橋一次， 並回到起點？ (Ch 7 Euler graph) Ch 1 -3 Copyright 黃鈴玲

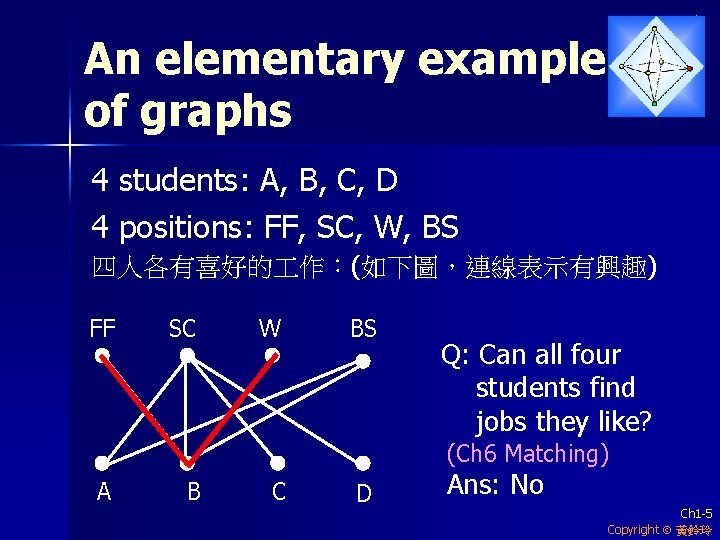
An elementary example of graphs 4 students: A, B, C, D 4 positions: FF, SC, W, BS 四人各有喜好的 作：(如下圖，連線表示有興趣) FF SC W BS Q: Can all four students find jobs they like? (Ch 6 Matching) A B C D Ans: No Ch 1 -5 Copyright 黃鈴玲

Definition of a graph n A graph G is a finite nonempty set V(G) of vertices (also called nodes, 點) and a (possibly empty) set E(G) of 2 -element subsets of V(G) called edges (or lines, 邊). V(G) : vertex set of G (只有一個 G 時常簡寫為 V) E(G) : edge set of G (只有一個 G 時常簡寫為 E) 常見的 edge 表示法: {u, v} = {v, u} = uv (or vu) 當邊有方向性時稱 G 為 directed graph (digraph) Ch 1 -6 Copyright 黃鈴玲

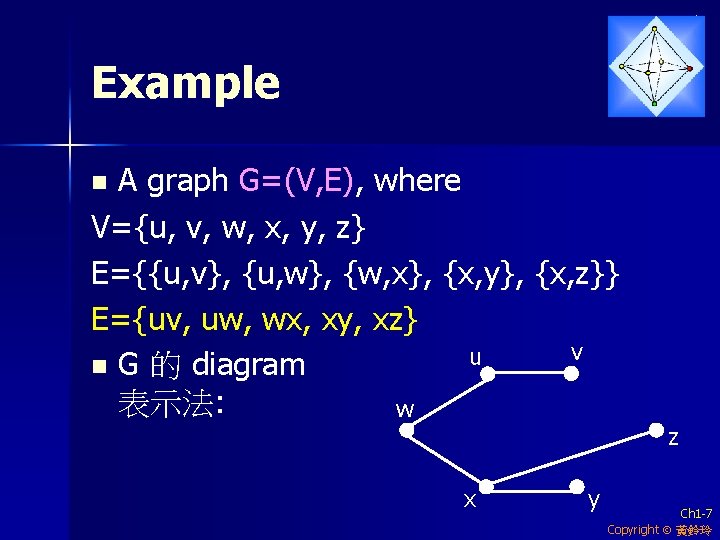
Example A graph G=(V, E), where V={u, v, w, x, y, z} E={{u, v}, {u, w}, {w, x}, {x, y}, {x, z}} E={uv, uw, wx, xy, xz} v u n G 的 diagram 表示法: w n x y z Ch 1 -7 Copyright 黃鈴玲

Adjacent and Incident n u, v : vertices of a graph G e u v u and v are adjacent in G if uv E(G) ( u is adjacent to v, v is adjacent to u) n e=uv (e joins u and v) (e is incident with u, e is incident with v) n Ch 1 -8 Copyright 黃鈴玲

Graphs types loop n multiedges, parallel edges undirected graph: • (simple) graph: loop ( ), multiedge ( ) • multigraph: loop ( ), multiedge ( ) • Pseudograph: loop ( ), multiedge ( ) Ch 1 -9 Copyright 黃鈴玲

order and size n n The number of vertices in a graph G is called its order (denoted by |V(G)| ). The number of edges is its size (denoted by |E(G)| ). Proposition 1: If |V(G)| = p and |E(G)| = q, then A graph of order p and size q is called a (p, q) graph. Ch 1 -10 Copyright 黃鈴玲

Application of graphs 一群人間兩兩互相認識或不認識(i. e. , 沒有A認識B但 B不認識A的情形)，在安排一張圓桌的晚餐座位時， 是否存在一種排法能讓坐在一起的人都相互認識？ eg. Tom, Dick know Sue, Linda. Harry knows Dick and Linda. acquaintance graph: n (連線表示認識) Q: 圖中是否有一個通過 所有點的cycle? (Ch 8 Hamiltonian graph) Tom Dick Harry Sue Linda Ch 1 -11 Copyright 黃鈴玲

Homework n Exercise 1. 1: 1, 2, 3, 4 Ch 1 -13 Copyright 黃鈴玲

Outline 1. 1 1. 2 1. 3 1. 4 1. 5 1. 6 1. 7 1. 8 1. 9 What is a graph? The Degree of a Vertex Isomorphic Graphs Subgraphs Degree Sequences Connected Graphs Cut-Vertices and Bridges Special graphs Digraphs Ch 1 -14 Copyright 黃鈴玲

1. 2 The degree of a vertex Definition. For a vertex v of G, its neighborhood N(v) = { u V(G) | v u E(G) }. The degree of vertex v is deg(v) = | N(v) |. u v N(u) = {x, w, v}, N(y)={ } y x deg(u) = 3, deg(y) =0 w Ch 1 -15 Copyright 黃鈴玲

Notes If |V(G)| = p, then 0 deg(v) p-1, v V(G). n If deg(v) = 0, then v is called an isolated vertex (孤立點). n v is an odd vertex if deg(v) is odd. v is an even vertex if deg(v) is even. n Ch 1 -16 Copyright 黃鈴玲

Handshaking theorem Theorem 1. 1 (Handshaking theorem) Let G be a graph, n Example u 2 x v 3 w 1 2 pf. 在計算degree總和時，每條邊會被計算兩次。 Ch 1 -17 Copyright 黃鈴玲

Handshaking theorem Corollary 1. 1 Every graph contains an even number of odd vertices. pf. If the number of vertices with odd degree is odd, then the degree sum must be odd. Ch 1 -18 Copyright 黃鈴玲

Regular graph Definition. A graph G is r-regular if every vertex of G has degree r. A graph G is regular if it’s r-regular for some r. Example Note. There is no 1 -regular graph or 3 -regular graph of order 5. (by Corollary 1. 1) 2 -regular Ch 1 -19 Copyright 黃鈴玲

Complement Definition. The complement G of a graph G is a graph with V(G) = V(G), and uv E(G) iff uv E(G). u v G u v w x G w x Ch 1 -20 Copyright 黃鈴玲

Application of degree Q: n people. (n 2) Is it possible that every two of them are acquainted with a different number of people in the group? (Suppose if A knows B, then B knows A. ) A: Consider the acquaintance graph。 若任兩人所認識的人數不等， 表示圖形中所有點的 degree 都不相等。 n 點的圖形中， degree 只可能是 0, 1, …, n-1 (共 n 種)， 必有一點 x 的 degree 為 0，另一點 y 的 degree 為 n-1， 也就是 x 不認識 y ，但 y 認識 x ，矛盾。 Ch 1 -21 Copyright 黃鈴玲

Exercise 1 Prove that every graph of order n 2 has at least two vertices with the same degree. (Hint. The problem in previous page. ) pf. If not, then there exist vertices x and y with deg(x) = 0 and deg(y) = n-1. It’s impossible. Ch 1 -22 Copyright 黃鈴玲

Exercise 9. Every vertex of a graph G of order 14 and size 25 has degree 3 or 5. How many vertices of degree 3 does G have? sol. Suppose there are x vertices of degree 3, then there are 14 -x vertices of degree 5. |E(G)| =25 degree sum=50 3 x + 5(14 -x) = 50 x = 10 Ch 1 -23 Copyright 黃鈴玲

Exercise 10. A graph G of order 7 and size 10 has six vertices of degree a and one of degree b. What is b? Try to draw the graph sol. 6 a + b = 20 (a, b) = (0, 20) (1, 14) (2, 8) (3, 2) a=3, b=2. ( ) ( ) Ch 1 -24 Copyright 黃鈴玲

Homework n Exercise 1. 2: 4, 7, 11 Ch 1 -25 Copyright 黃鈴玲

Outline 1. 1 1. 2 1. 3 1. 4 1. 5 1. 6 1. 7 1. 8 1. 9 What is a graph? The Degree of a Vertex Isomorphic Graphs Subgraphs Degree Sequences Connected Graphs Cut-Vertices and Bridges Special graphs Digraphs Ch 1 -26 Copyright 黃鈴玲

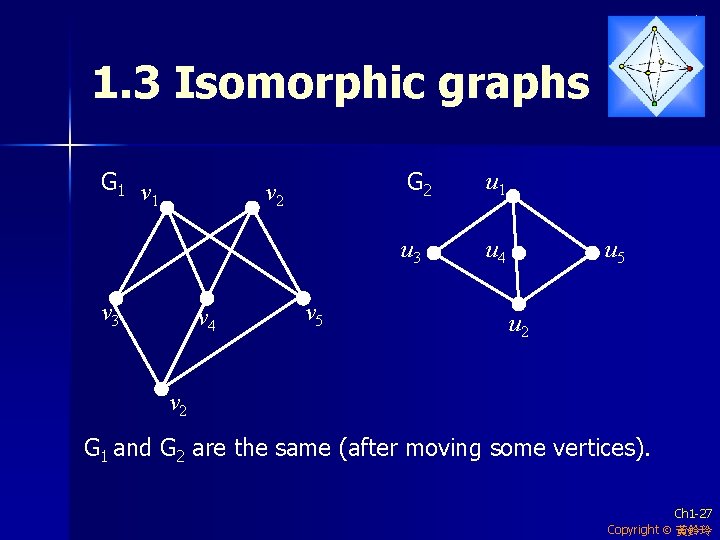
1. 3 Isomorphic graphs G 1 v 2 v 3 v 4 v 5 G 2 u 1 u 3 u 4 u 5 u 2 v 2 G 1 and G 2 are the same (after moving some vertices). Ch 1 -27 Copyright 黃鈴玲

Isomorphic Definition. Two graph G 1 and G 2 are isomorphic (同構) (denoted by G 1 G 2 ) if there is a 1 -1 and onto function from V(G 1) to V(G 2) such that uv E(G 1) iff (u) (v) E(G 2). (對應過去後，仍能保持兩點間相連與否的關係) The function is called an isomorphism. In previous page, f (vi) = ui for each i. Ch 1 -28 Copyright 黃鈴玲

Isomorphic Definition. Two graph G 1 and G 2 are equal if V(G 1) = V(G 2) and E(G 1) = E(G 2). Proposition. 1. If G 1 G 2, then |V(G 1)| = |V(G 2)| and |E(G 1)| = |E(G 2)|. 2. If G 1 G 2 and is an isomorphism from V(G 1) to V(G 2), then (So the degree sequences of these graphs must be the same. ) 1 跟 2 是判斷兩個圖是否 isomorphic 的初步檢查條件 Ch 1 -29 Copyright 黃鈴玲

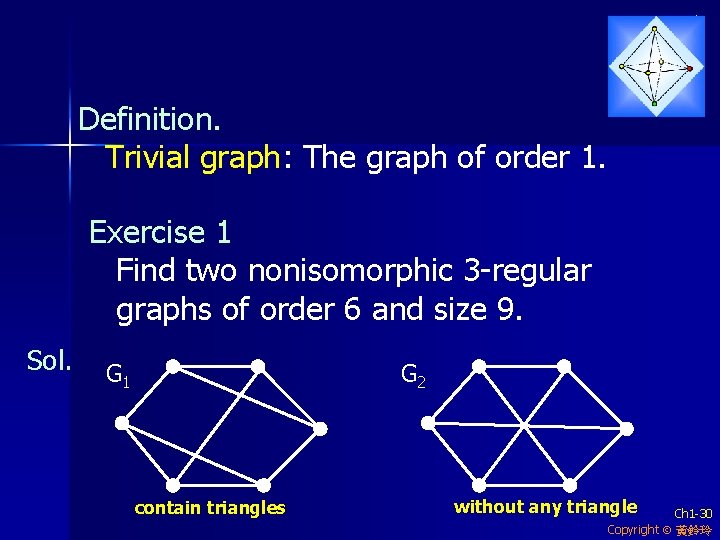
Definition. Trivial graph: The graph of order 1. Exercise 1 Find two nonisomorphic 3 -regular graphs of order 6 and size 9. Sol. G 1 G 2 contain triangles without any triangle Ch 1 -30 Copyright 黃鈴玲

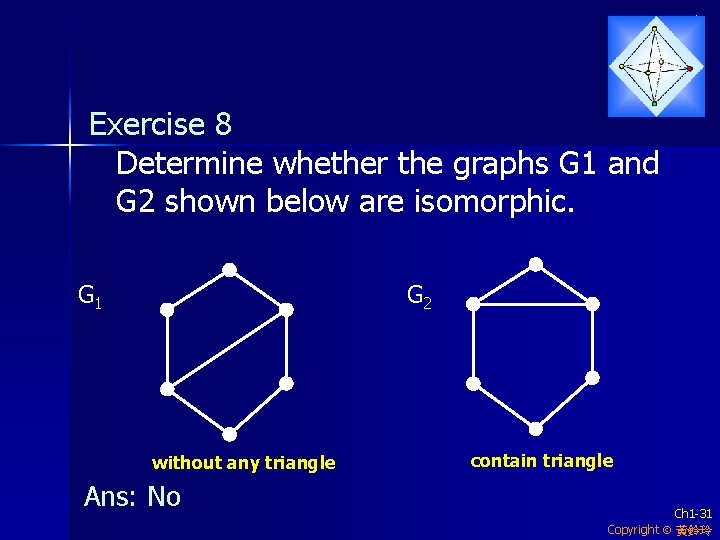
Exercise 8 Determine whether the graphs G 1 and G 2 shown below are isomorphic. G 1 G 2 without any triangle Ans: No contain triangle Ch 1 -31 Copyright 黃鈴玲

Homework n Exercise 1. 3: 4, 7, 9 Ch 1 -33 Copyright 黃鈴玲

Outline 1. 1 1. 2 1. 3 1. 4 1. 5 1. 6 1. 7 1. 8 1. 9 What is a graph? The Degree of a Vertex Isomorphic Graphs Subgraphs Degree Sequences Connected Graphs Cut-Vertices and Bridges Special graphs Digraphs Ch 1 -34 Copyright 黃鈴玲

1. 4 Subgraphs Definition. A graph H is a subgraph of a graph G if V(H) V(G) and E(H) E(G). (denote H G) Example v w v w u y x G y x H G y x F G Ch 1 -35 Copyright 黃鈴玲

Induced Subgraph Definition. Let S V(G), S . The subgraph induced by S is the maximal subgraph of G with vertex set S. (denoted by <S>) A subgraph H of a graph G is a vertex-induced subgraph if H=<S> for some S V(G). G v w H v w u x y H is not an induced subgraph of G. H ∪{xw}才是 Ch 1 -36 Copyright 黃鈴玲

The deletion of vertices Definition. Let S V(G). The graph G-S = <V(G)-S>. If S={v}, then we write G-v instead. G v G-S w Let S={x, u} u x y v w u x y Ch 1 -37 Copyright 黃鈴玲

Edge Induced Subgraph Definition. Let X E(G), X . The subgraph induced by X is the minimal subgraph of G with edge set X. (denoted by <X>) A subgraph H of a graph G is an edge-induced subgraph if H=<X> for some X E(G). G v <X> w Let X={uv, vw} u x v w u y Ch 1 -38 Copyright 黃鈴玲

Definition. A subgraph H G is a spanning subgraph of G if V(H) = V(G). Definition. H = G + {uv, uw} means E(H) = E(G) ∪ {uv, uw} , where uv, uw E(G). Exercise 5 If H=<E(G)>, does it follows that H=<V(G)>? u No G v w H v w Ch 1 -39 Copyright 黃鈴玲

Homework Exercise 6 Let G be a labeled (p, q) graph. How many different edge-induced subgraphs does G have? Note. 不同的邊集合會造出不同的 edge-induced subgraph q q Ans. 2 -1 ( X E(G) 且 X , 共有 2 -1 種 X ) n Exercise 1. 4: 1, 3 Ch 1 -40 Copyright 黃鈴玲

Outline 1. 1 1. 2 1. 3 1. 4 1. 5 1. 6 1. 7 1. 8 1. 9 What is a graph? The Degree of a Vertex Isomorphic Graphs Subgraphs Degree Sequences Connected Graphs Cut-Vertices and Bridges Special graphs Digraphs Ch 1 -41 Copyright 黃鈴玲

1. 5 Degree Sequence Definition. Let G=(V, E), V={v 1, v 2, …, vp}. Then s: deg(v 1), deg(v 2), …, deg(vp) is called a degree seqence of G. (For convenient, assume s is nonincreasing, then s is unique. ) G 3 2 s: 3, 3, 2, 1, 1, 0 1 0 3 minimum degree : d(G) 1 maximum degree : D(G) Ch 1 -42 Copyright 黃鈴玲

Note l If d 1, d 2, …, dp is the degree sequence of some graph, then and 0 d i p-1 i. l For a given sequence s: d 1, d 2, …, dp of integers such that and 0 d i p-1 i, there is no guarantee that s is the degree sequence of some graph. ( p-1 and 0 can’t exist ex. s: 5, 5, 3, 2, 1, 0 at the same time) (Moreover, d 1 p is impossible. ) Ch 1 -43 Copyright 黃鈴玲

Definition. We call a sequence of nonnegative integers graphical if it is the degree sequence of some graph. Theorem 1. 2 (Havel-Hakimi) Let s be a sequence: d 1, d 2, …, dp, where di N, i. Let s 1 be the sequence: Then s is graphical iff s 1 is graphical. (Note. s 1 即是把 d 1 扣掉，剩下的前 d 1 項各減 1。) Ch 1 -44 Copyright 黃鈴玲

Proof of Thm 1. 2: ( ) If s 1 : is graphical graph G 1 s. t. s 1 is the degree sequence of G 1 d 2 -1 d 3 -1 d 1 vertices v 2 v 3 -1 1+1 dd vd dp 1+2 1+1 vd 1+1 dd … G 1 dd 1+2 vp … d 2 v 2 G dd d 3 vd … 1+1 dp 1+2 vd 1+2 vp … … v 1 s : d 1, d 2, …, dp is graphical. Ch 1 -45 Copyright 黃鈴玲

Proof of Thm 1. 2: (continued) ( ) If s : d 1, d 2, …, dp is graphical graph G s. t. s is the degree sequence of G with deg(vi) = di for 1 i p, and is maximum. Claim: { v 1 v 2, v 1 v 3, …, v 1 vd 1+1} E(G) i. e. , G d 1 d 2 d 3 v 1 v 2 v 3 dd 1+1 vd … 1+1 dd dp 1+2 vd 1+2 vp … : : If the claim is true, then G-v 1 is a graph with degree sequence s 1 is graphical. Ch 1 -46 Copyright 黃鈴玲

Claim: { v 1 v 2, v 1 v 3, …, v 1 vd 1+1} E(G) Proof: If not, there must be two vertices vj and vk (j < k) with dj > dk s. t. v 1 vk E(G) but v 1 vj E(G). G v 1 vj vk vn Since dj > dk, vn V(G) s. t. vjvn E(G), vkvn E(G). Let G 2 = G - {v 1 vk, vjvn} + {v 1 vj, vkvn} G 2 has degree seq s but larger , Ch 1 -47 Copyright 黃鈴玲

Algorithm s: d 1, d 2, …, dp sequence of integers To determine whether s is graphical: (1) If di=0, i, then s is graphical. If di<0 for some i, then s is not graphical. Otherwise, go to (2) Reorder s to a nonincreasing sequence if necessary. (3) Let s = s 1, (s 1的產生方式同 Thm 1. 2), return to (1). Ch 1 -48 Copyright 黃鈴玲

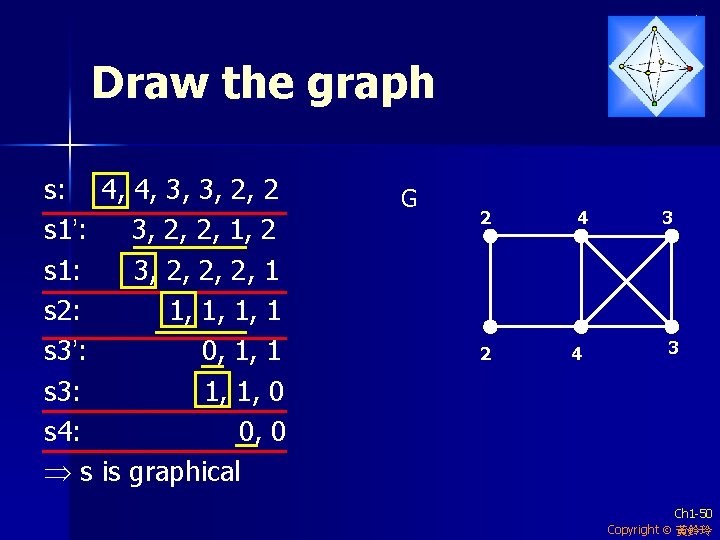
Example 1 s: 4, 4, 3, 3, 2, 2 s 1’: 3, 2, 2, 1, 2 s 1: 3, 2, 2, 2, 1 s 2: 1, 1, 1, 1 s 3’: 0, 1, 1 s 3: 1, 1, 0 s 4: 0, 0 s is graphical (delete the first 4) (reorder) (delete 3) (delete the first 1) (reorder) (delete the first 1) Ch 1 -49 Copyright 黃鈴玲

Draw the graph s: 4, 4, 3, 3, 2, 2 s 1’: 3, 2, 2, 1, 2 s 1: 3, 2, 2, 2, 1 s 2: 1, 1, 1, 1 s 3’: 0, 1, 1 s 3: 1, 1, 0 s 4: 0, 0 s is graphical G 2 2 4 4 3 3 Ch 1 -50 Copyright 黃鈴玲

Example 2 s: 5, 4, 3, 2, 1, 1 s 1: 3, 2, 1, 0, 0 (delete 5) s 2: 1, 0, -1, 0 (delete 3) s is not graphical Ch 1 -51 Copyright 黃鈴玲

Definition. Let G=(V, E), the set D (G)={deg(v) | v V } is called the degree set of G. Ex. s: 4, 4, 3, 3, 2, 2 D (G)={ 2, 3, 4 } (去掉順序及重複性) Kapoor et al [7] showed that Every finite set of nonnegative integers is the degree set of some graph. Ch 1 -52 Copyright 黃鈴玲

Exercise 6 Let |V(G)|=12, D (G) {4, 5, 6}. Show that G contains either (i) at least 4 vertices of degree 4, (ii) at least 6 vertices of degree 5, (iii) at least 5 vertices of degree 6. Proof If not, deg 4 點數 3 deg 4 點數 = 3 deg 5 點數 = 5 deg 5 點數 5 3+5+4=12 deg 6 點數 = 4 deg 6 點數 4 degree總和不為偶數 Ch 1 -53 Copyright 黃鈴玲

Exercise 8 Let G be a graph with D (G) = {m, n}, where G contains m vertices of degree m and n vertices of degree n. Prove that if G contains an odd vertex, then every vertex of G is odd. Proof degree sum = m 2 + n 2 If m is odd then n must be odd, and vice versa. Ch 1 -54 Copyright 黃鈴玲

Homework n Exercise 1. 5: 1, 3, 5, 7, 9 Ch 1 -55 Copyright 黃鈴玲

Outline 1. 1 1. 2 1. 3 1. 4 1. 5 1. 6 1. 7 1. 8 1. 9 What is a graph? The Degree of a Vertex Isomorphic Graphs Subgraphs Degree Sequences Connected Graphs Cut-Vertices and Bridges Special graphs Digraphs Ch 1 -56 Copyright 黃鈴玲

1. 6 Connected graphs Definition. A walk in a graph G is an alternating sequence W: v 0, e 1, v 1, e 2, v 2, …, vn-1, en, vn (n 0) of vertices and edges, where ei=vi-1 vi, i. ( 故 W 中的 ei 可省略) (W is also called a v 0 -vn walk) W is said to have length n. A trail is a walk without repeated edges. A path is a walk without repeated vertices. G v w u x y walk: x, w, v, x, w trail: x, w, v, x, y path: x, w, v Ch 1 -57 Copyright 黃鈴玲

Theorem 1. 3 Every u-v walk in a graph contains a u-v path. Proof. 去掉重複的點或邊即可 Definition (1) A cycle is a walk v 0, v 1, v 2, …, vn-1, vn in which n 3, v 0 = vn, and v 1, v 2, …, vn-1, vn are distinct. (n-cycle) (2) A u-v walk is closed if u=v. (closed walk) (3) A nontrivial closed trail is called a circuit. Ch 1 -58 Copyright 黃鈴玲

Definition (1) Let u, v V(G), u is connected to v if u-v path. (2) G is connected if u is connected to v u, v V(G), otherwise, G is called disconnected. (3) A subgraph H of G is a component of G if H is a maximal connected subgraph of G. (4) The number of components of G is denoted by k (G). Note. “is connected to” is an equivalence relation Ch 1 -59 Copyright 黃鈴玲

Exercise 7 Let G be a graph. |V(G)|=p, p 2. Suppose d(G) (p-1)/2. Prove that G is connected. Proof If G is disconnected, since d(G) (p-1)/2, each component must contain (p+1)/2 vertices. Ch 1 -60 Copyright 黃鈴玲

Exercise 10 Prove that if a graph G has a closed walk of odd length, then it has a cycle of odd length. Proof. (1) 若點沒有重複 此walk本身即odd cycle (2) 若點 x 重複出現 設此walk P: v 0=x, v 1, v 2, …, vi=x, vi+1, …, vn, v 0=x 其中 vi 是從v 0走到vn的過程中， x 最後一次出現 則可將P分成兩個closed walk: P 1: v 0=x, v 1, v 2, …, vi=x P 2: vi=x, vi+1, …, vn, v 0=x 兩者必有一為odd length 取此一walk仿照上述方法再拆，最後必可得一odd cycle. Ch 1 -61 Copyright 黃鈴玲

Exercise 11 Show that a graph G contains (1) a path of length d(G), and (2) a cycle of length at least d(G) +1 if d(G) 2. Proof: Let P: v 0, v 1, …, vk be a longest path of G. Then deg(v 0) d(G), and N(v 0 ) V(P) for otherwise P is not longest. It follows that the length of P is at least d(G). Let vn be the vertex of P with v 0 vn E(G) and n is largest. If d(G) 2, 2 then n 2. Let C: v 0, v 1, …, vn, v 0. Since N(v 0) V(C), It is clear that the length of C is at least d(G) +1. Ch 1 -62 Copyright 黃鈴玲

Homework n Exercise 1. 6: 1, 2, 3, 4, 5, 8, 9 Ch 1 -63 Copyright 黃鈴玲

Outline 1. 1 1. 2 1. 3 1. 4 1. 5 1. 6 1. 7 1. 8 1. 9 What is a graph? The Degree of a Vertex Isomorphic Graphs Subgraphs Degree Sequences Connected Graphs Cut-Vertices and Bridges Special graphs Digraphs Ch 1 -64 Copyright 黃鈴玲

1. 7 Cut Vertices and Bridges Definition 1 A vertex v in a graph G is called a cut -vertex if k(G - v) > k(G). So v is a cut-vertex in a connected graph G if G - v is disconnected. Ch 1 -65 Copyright 黃鈴玲

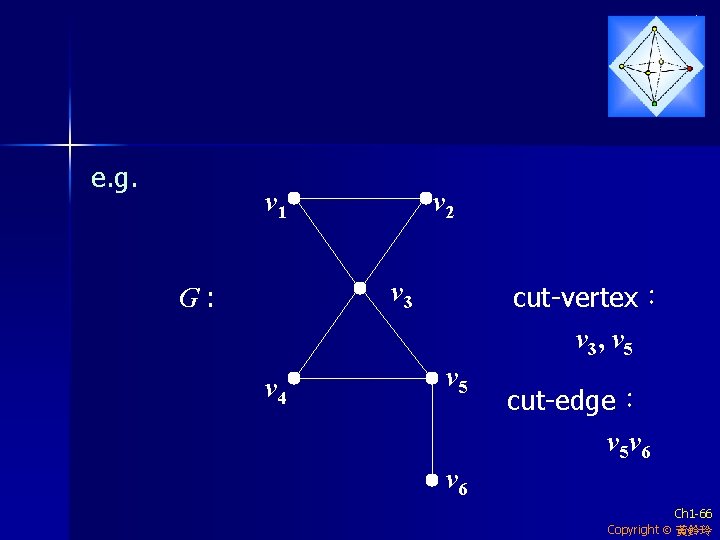
e. g. v 1 v 2 v 3 G: 　　　　　　 v 4 cut-vertex： v 3, v 5 cut-edge： v 5 v 6 Ch 1 -66 Copyright 黃鈴玲

Definition 2 An edge e in a graph G is called a bridge (cut-edge) if k(G - e) > k(G). e. g. The graph in previous page: v 5 v 6 is a bridge. Note. (1) if v is a cut-vertex of a connected graph G, then k(G - v) 2 (2)If e is a bridge of a connected graph G, then k(G - e) =2 Ch 1 -67 Copyright 黃鈴玲

Theorem 1. 4 An edge e of a connected graph G is a bridge iff e does not lie on a cycle of G. Proof. ( ) Let e be a bridge of G. Suppose e =uv, and assume, to the contrary, that e lies on a cycle C：u, v, w, …, x, u. 　Then C - e：v, w, …, x, u is a u-v path of G - e. Claim: G - e is connected. (If the claim is true, (e is not) a bridge) Ch 1 -68 Copyright 黃鈴玲

(Proof of above Claim) Let u 1, v 1 V(G-e)=V(G) ∵G is connected ∴ u 1 -v 1 path P in G. If e P, then P is also a path in G-e u 1 -v 1 path in G-e If e P, then (P C)-e is a u 1 -v 1 walk in G-e ∴ u 1 -v 1 path in G-e C P Therefore, G-e is connected. u 1 u v v 1 Ch 1 -69 Copyright 黃鈴玲

( ) Suppose e=uv is an edge that lies on no cycle of G. Then G-e contains no u-v path. Otherwise, if P is a u-v path in G-e, then P { uv } is a cycle containing e, . Ch 1 -70 Copyright 黃鈴玲

Definition 3 # of vertices 2 A nontrivial connected graph without a cut-vertex is called a nonseparable graph. A block B of a nontrivial connected graph G is a subgraph of G that itself is a maximal nonseparable graph. Ch 1 -71 Copyright 黃鈴玲

e. g. G v 1 v 2 <{v 1, v 2, v 3}>, <{v 3, v 4, v 5}>, <{v 5, v 6}> v 3 v 4 G has 3 blocks： v 5 v 6 Ch 1 -72 Copyright 黃鈴玲

Note: 1. A block is necessarily an induced subgraph. 2. The blocks of a graph produce a partition of the edge set of the graph. 3. Every two blocks have at most one vertex in common. 4. If v V(B 1) V(B 2), where B 1, B 2 are block of G, then v is a cut-vertex. 5. If G is nonseparable, then G is a block. Ch 1 -73 Copyright 黃鈴玲

Definition A block of a graph G that contains exactly one cut-vertex of G is called an end-block of G. Theorem 1. 5 Let G be a connected graph with at least one cut-vertex. Then G has at least two end-blocks. (介紹到tree時再証) Ch 1 -74 Copyright 黃鈴玲

Homework n Exercise 1. 7: 1, 2, 4, 5, 6, 7 Ch 1 -75 Copyright 黃鈴玲

HW 3 (a) Show that if G is an r-regular connected graph, where r is even, then G contains no bridges. (b) Is the statement in (a) still true if r is odd? Sol： (a) If G has a bridge e, assume G = G 1 G 2 {e}, where e=ab, G 1 and G 2 are the two components of Ge. G 1 a b G 2 Ch 1 -76 Copyright 黃鈴玲

Consider the subgraph G 1 v V(G 1), deg. G (v)= r if v a r-1 if v=a ∵r is even ∴ is odd 1 Ch 1 -77 Copyright 黃鈴玲

(b) No, e. g. r = 1 G： r=3 G： Ch 1 -78 Copyright 黃鈴玲

HW 4 Find a counterexample (a) If G is a connected graph that contains only even vertices, then G contains no cut-vertices. Sol. Ch 1 -79 Copyright 黃鈴玲

HW 8 A connected graph G contains three distinct vertices u, v and w with the property that every u-w path in G contains v. Show that v is a cut-vertex. Proof. Consider G-v, there is no u-w path in G-v. k(G-v)>1 = k(G) v is a cut-vertex. Ch 1 -80 Copyright 黃鈴玲

Outline 1. 1 1. 2 1. 3 1. 4 1. 5 1. 6 1. 7 1. 8 1. 9 What is a graph? The Degree of a Vertex Isomorphic Graphs Subgraphs Degree Sequences Connected Graphs Cut-Vertices and Bridges Special graphs Digraphs Ch 1 -81 Copyright 黃鈴玲

1. 8 Special Graphs Def 1. Complete graph (Kp) : p vertices, p 1 , u~v, u, v V (Kp) Note. (1) Kp is (p-1) regular (2) Kp has edges. K 5 Ch 1 -82 Copyright 黃鈴玲

Def 2. A path of order n (denoted by Pn) : a path of n vertices. (length n-1) Def 3. n-cycle (denoted by Cn) : a cycle of n vertices, n 3. even cycle : a cycle of even vertices odd cycle : a cycle of odd vertices P 4 C 5 Ch 1 -83 Copyright 黃鈴玲

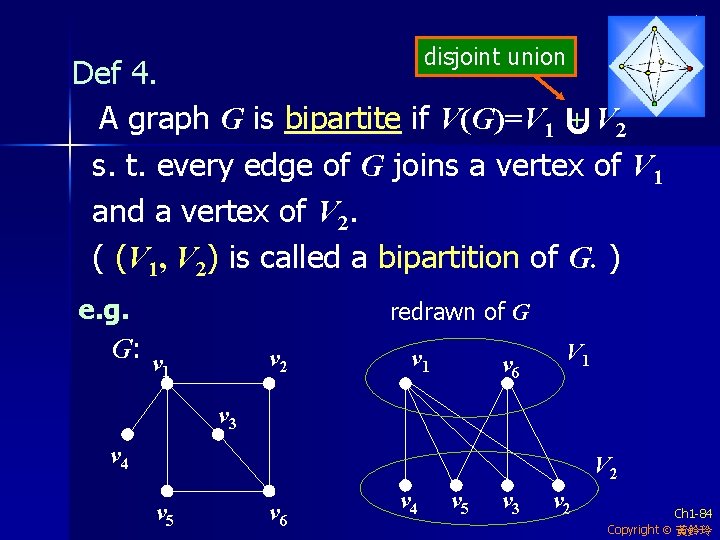
disjoint union Def 4. + V 2 A graph G is bipartite if V(G)=V 1 ∪ s. t. every edge of G joins a vertex of V 1 and a vertex of V 2. ( (V 1, V 2) is called a bipartition of G. ) e. g. G: v 1 redrawn of G v 2 v 1 v 6 V 1 v 3 v 4 V 2 v 5 v 6 v 4 v 5 v 3 v 2 Ch 1 -84 Copyright 黃鈴玲

Def 5. (先補充) If u-v path in G , the distance between u and v, denoted by d(u, v), is the length of shortest u-v path. If u-v path in G, d(u, v) = ∞. e. g. 上圖 G 中 v 2 v 1 d(v 1, v 4) = 1 d(v 1, v 6) = 2 v 3 d(v 4, v 6) = 3 v 4 v 5 v 6 Ch 1 -85 Copyright 黃鈴玲

Thm 1. 6 A nontrivial graph G is bipartite iff G has no odd cycles. Pf: ) Assume G is a bipartite graph with bipartition (V 1, V 2). If Cn : v 1, v 2, …, vn, v 1 is any cycle of G. (n 3) Suppose v 1 V 1, then v 2 V 2, v 3 V 1, v 4 V 2, …, vn V 2 Hence n must be even, G has no odd cycles. Ch 1 -86 Copyright 黃鈴玲

) It clearly suffices to prove the converse of connect graphs. Let G be a connected graph without odd cycles. Choose any vertex u V(G), define V 1 = { w V(G) | d(u, w) is even} V 2 = { w V(G) | d(u, w) is odd} (Show that (V 1, V 2) is a bipartition of G). Ch 1 -87 Copyright 黃鈴玲

Choose any two vertices v, w V 1 (or v, w V 2 ). Let P be a shortest u-v path and Q be a shortest u-w path. (P, Q may have several common vertices. ) Let u 1 be the last vertex common to P and Q. Let P’ be the subpath of P connecting u 1 and v, Q’ be the subpath of Q connecting u 1 and w. length(P-P’) = length(Q-Q’) d(u 1, v)+d(u 1, w) is even. If vw E(G), then P’∪Q’∪{vw} is a cycle of odd length. u w P v ∴ vw E(G), v, w V 1 or v, w V 2 G is bipartite. u 1 Q Ch 1 -88 Copyright 黃鈴玲

Def 6. Complete bipartite graph Km, n : V(Km, n) = V 1∪ V 2 , where |V 1|=m , |V 2|=n. u V 1 and v V 2 , uv E(Km, n). Note : |V(Km, n)| = m+n |E | (Km, n)| = mn. K 3, 2 Ch 1 -89 Copyright 黃鈴玲

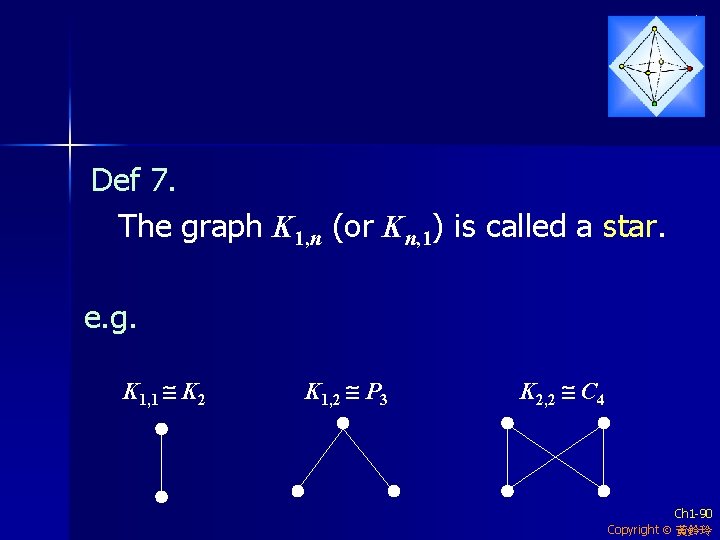
Def 7. The graph K 1, n (or Kn, 1) is called a star. e. g. K 1, 1 K 2 K 1, 2 P 3 K 2, 2 C 4 Ch 1 -90 Copyright 黃鈴玲

Def 7. (n-partite graph) (n 2) A graph G is an n-partite graph if V(G) can be partitioned into n nonempty subsets V 1, V 2, …, Vn such that no edge of G joins vertices in the same set. (V 1, V 2, …, Vn are called the partite sets of G) V 1 3 -partite graph V 3 V 2 Ch 1 -91 Copyright 黃鈴玲

Def 8. Complete n-partite graph Kp , …, p : 1 2 n + V 2∪ + …∪ + Vn V(Kp , …, p ) = V 1∪ 1 2 n where |Vi|=Pi , i E(Kp , …, p ) = {uv | u Vi , v Vj with i≠j } 1 2 n e. g. K 1, 1, 1, 1 K 4 Ch 1 -92 Copyright 黃鈴玲

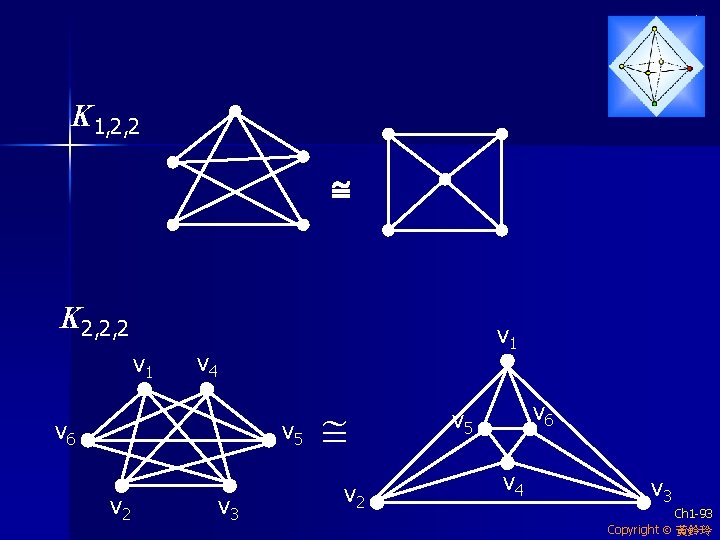
K 1, 2, 2 K 2, 2, 2 v 1 v 4 v 6 v 5 v 2 v 3 v 2 v 6 v 5 v 4 v 3 Ch 1 -93 Copyright 黃鈴玲

Def 9. Let G 1, G 2 be vertex-disjoint graphs. The union of G 1, G 2 is the graph G 1∪G 2 having V(G 1∪G 2) = V(G 1)∪V(G 2) E(G 1∪G 2) = E(G 1)∪E(G 2) If G 1 G 2 G then we write 2 G for G 1∪G 2. Ch 1 -94 Copyright 黃鈴玲

(2) The join of G 1, G 2 is the graph G 1+G 2 having V(G 1+G 2) = V(G 1)∪V(G 2) E ( G 1 + G 2 ) = E(G 1)∪E(G 2)∪{v 1 v 2 : v 1 V(G 1), v 2 V(G 2)} e. g. P 3 : P 3+K 2 : Ch 1 -95 Copyright 黃鈴玲

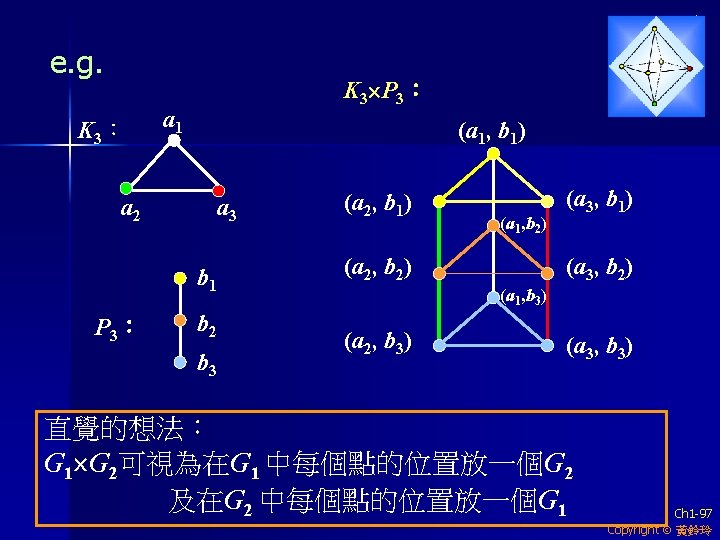
(3) For graphs G 1 and G 2, the product G 1 × G 2 has vertex set V(G 1×G 2)= V(G 1) × V(G 2) ={ (u 1, u 2) : u 1 V(G 1) , u 2 V(G 2)} and (u 1, u 2) ~ (v 1, v 2) iff u 1 = v 1 and u 2 v 2 E(G 2) or u 2= v 2 and u 1 v 1 E(G 1) Ch 1 -96 Copyright 黃鈴玲

Definition 10. 在考慮product時, 有一類圖形常被提到： The hypercube or n-cube Qn is defined as Q 1= K 2 Qn= Qn-1 K 2 if n 2 　 Q 1： Q 2： 0 1 (0, 0 ) (1, 0 ) (0, 1 ) (1, 1 ) Ch 1 -98 Copyright 黃鈴玲

Q 3： (0, 0, 1) (0, 1, 0) (0, 0, 0) (1, 0, 1) (1, 0, 0) (1, 1, 1) (1, 1, 0) Note. V(Qn) can be written as {(a 1, a 2, …, an) | ai=0 or 1} Ch 1 -99 Copyright 黃鈴玲

Homework n Exercise 1. 8: all, except 10(b)(c) , 11 Ch 1 -100 Copyright 黃鈴玲

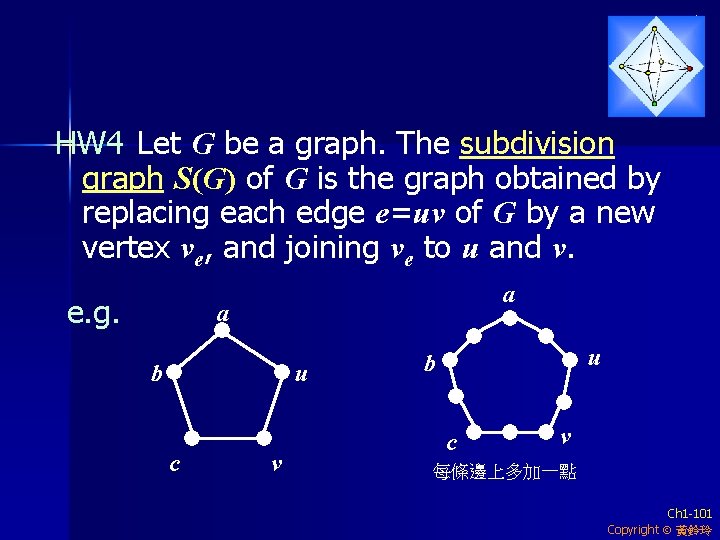
HW 4 Let G be a graph. The subdivision graph S(G) of G is the graph obtained by replacing each edge e=uv of G by a new vertex ve, and joining ve to u and v. e. g. a a b u c v u b c v 每條邊上多加一點 Ch 1 -101 Copyright 黃鈴玲

HW 4 (continued) Show that if G is any nontrivial graph, then S(G) is bipartite. Proof. Let V(S(G)) = V(G) D, where D={ve：e E(G)} Then u, v V(G), u ~ v in S(G) and w, x D, w ~ x in S(G) So (V(G), D) is a bipartition of S(G). # Ch 1 -102 Copyright 黃鈴玲

HW 9 Let G be a graph with the property that every edge joins an even vertex and an odd vertex. Prove that G is bipartite. Proof. (Method 1) If not, G has an odd cycle odd even odd contradiction Ch 1 -103 Copyright 黃鈴玲

(method 2) + V , Let V(G)=V 1 2 where V 1 = {all even vertices} V 2 = {all odd vertices} then (V 1, V 2) is a bipartition of G. Ch 1 -104 Copyright 黃鈴玲

Outline 1. 1 1. 2 1. 3 1. 4 1. 5 1. 6 1. 7 1. 8 1. 9 What is a graph? The Degree of a Vertex Isomorphic Graphs Subgraphs Degree Sequences Connected Graphs Cut-Vertices and Bridges Special graphs Digraphs Ch 1 -105 Copyright 黃鈴玲

1. 9 Digraphs Definition 1: A digraph (or directed graph) D is a finite, nonempty set V(D) of vertices and a set E(D) of ordered pairs of distinct vertices. The elements of E(D) are called arcs. e. g. D: u w v x E(D) ={(v, u), (u, w), (v, w), (x, w), (w, x)} Ch 1 -106 Copyright 黃鈴玲

Definition 2: The underlying graph of a diagraph D: 去掉邊的方向性後得到的simple graph. w (Note: becomes x w ) x Definition 3: u v u is adjacent to v v is adjacent from u (u, v) is incident from u and incident to v. Ch 1 -107 Copyright 黃鈴玲

Definition 4: v v Thm 1. 7: outdegree of v : od v (textbook) , deg+(v) indegree of v : id v, deg -(v) Let D be a digraph, then ※ Many properties are similar with simple graphs, but the length of a cycle can be 2. Ch 1 -108 Copyright 黃鈴玲

Definition 5: semiwalk : 不管邊之方向性的walk W : e 1 v 0 e 2 v 1 e 3 v 2 e 4 v 3 v 4 … vn (ei = (vi-1, vi) or (vi, vi-1) ) Definition 6: Two vertices u and v in a digraph D are connected if D contains a u-v semiwalk. Ch 1 -109 Copyright 黃鈴玲

Definition 7: ① A diagraph D is connected if every two vertices of D are connected. (also called weakly connected) ② A diagraph is (單方向的) unilaterally connected if for every two distinct vertices u and v there is a u-v path or a v-u path. ③ A diagraph is strongly connected if for every two distinct vertices u and v there is a u-v path and a v-u path. Definition 8: G is symmetric if u v G is asymmetric if u v v u Ch 1 -110 Copyright 黃鈴玲

Definition 9: multidigraph : allowed pseudodigraph: allowed v u v and u Definition 10: A digraph D in which either u is called a or u (not both) tournament. v v u, v V(D) Ch 1 -111 Copyright 黃鈴玲

Homework n Exercise 1. 9: 3, 8, 10, 11 HW 3: Show that a strong (strongly connected) digraph of order p 2 contains a cycle of length n for some n 2. Ch 1 -112 Copyright 黃鈴玲