UNIT I PART II FINITE AUTOMATA Finite Automata

UNIT I PART II FINITE AUTOMATA

Finite Automata • Definition: A finite automaton (FA) is a simple idealized machine used to recognize patterns within input taken from some character set (or alphabet). • The job of an FA is to accept or reject an input depending on whether the pattern defined by the FA occurs in the input. • Finite Automata(FA) is the simplest machine to recognize patterns. • • A Finite Automata consists of the following : Q : Finite set of states. Σ : set of Input Symbols. q : Initial state. F : set of Final States. δ : Transition Function. Formal specification of machine is { Q, Σ, q, F, δ }.

Types of FA • FA is characterized into two types: • § § § 1) Deterministic Finite Automata (DFA) DFA consists of 5 tuples {Q, Σ, q, F, δ}. Q : set of all states. Σ : set of input symbols. ( Symbols which machine takes as input ) q : Initial state. ( Starting state of a machine ) F : set of final state. δ : Transition Function, defined as δ : Q X Σ --> Q.

1. Deterministic Finite Automata(DFA) • In a DFA, for a particular input character, the machine goes to one state only. • A transition function is defined on every state for every input symbol. • Also in DFA null (or ε) move is not allowed, i. e. , DFA cannot change state without any input character. • For example, below DFA with Σ = {0, 1} accepts all strings ending with 0. • One important thing to note is, there can be many possible DFAs for a pattern. A DFA with minimum number of states is generally preferred.

2. Nondeterministic Finite Automata(NFA) • NFA is similar to DFA except following additional features a) Null (or ε) move is allowed i. e. , it can move forward without reading symbols. b) Ability to transmit to any number of states for a particular input. • However, these above features don’t add any power to NFA. If we compare both in terms of power, both are equivalent. • Due to above additional features, NFA has a different transition function, rest is same as DFA. • δ: Transition Function δ: Q X (Σ U ε ) --> 2 ^ Q. As you can see in transition function is for any input including null (or ε), NFA can go to any state number of states.

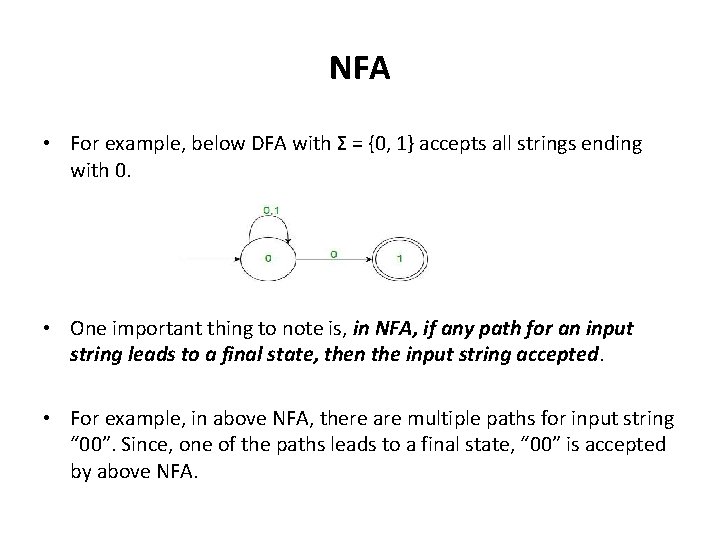
NFA • For example, below DFA with Σ = {0, 1} accepts all strings ending with 0. • One important thing to note is, in NFA, if any path for an input string leads to a final state, then the input string accepted. • For example, in above NFA, there are multiple paths for input string “ 00”. Since, one of the paths leads to a final state, “ 00” is accepted by above NFA.

Some Important Points: 1. Every DFA is NFA but not vice versa. Justification: • Since all the tuples in DFA and NFA are the same except for one of the tuples, which is Transition Function (δ) • In case of DFA δ : Q X Σ --> Q • In case of NFA δ : Q X Σ --> 2 Q • Now if you observe you’ll find out Q X Σ –> Q is part of Q X Σ –> 2 Q. • In the RHS side, Q is the subset of 2 Q which indicates Q is contained in 2 Q or Q is a part of 2 Q, however, the reverse isn’t true. So mathematically, we can conclude that every DFA is NFA but not vice-versa. Yet there is a way to convert an NFA to DFA, so there exists an equivalent DFA for every NFA. 2. Both NFA and DFA have same power and each NFA can be translated into a DFA. 3. There can be multiple final states in both DFA and NFA. 4. NFA is more of a theoretical concept. 5. DFA is used in Lexical Analysis in Compiler.

Applications of FA Ø Finite automata is used for solving several common types of computer algorithms. Some of them are: 1) Design of digital circuit. 2) String matching 3) Communication protocols for information exchange. 4) Lexical analysis phase of compiler. 5) FA can work as an algorithm for regular language. Ø It can be used for checking whether a string w ∈ L, where L is regular language.

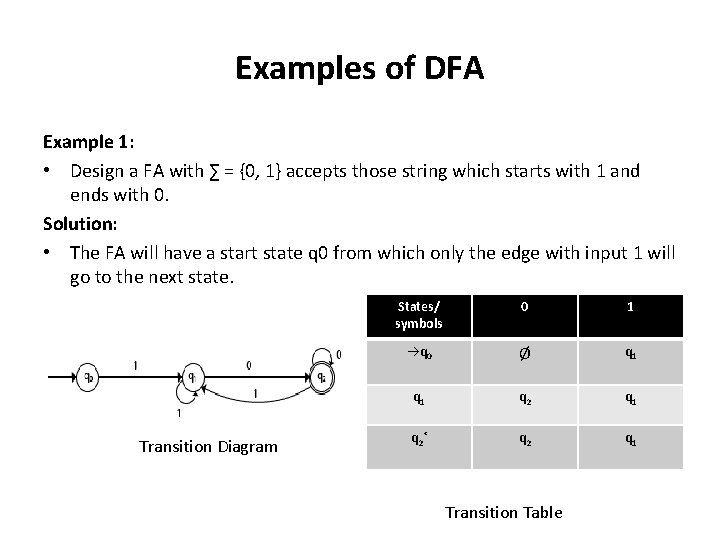
Examples of DFA Example 1: • Design a FA with ∑ = {0, 1} accepts those string which starts with 1 and ends with 0. Solution: • The FA will have a start state q 0 from which only the edge with input 1 will go to the next state. Transition Diagram States/ symbols 0 1 q 0 Ø q 1 q 2* q 2 q 1 Transition Table

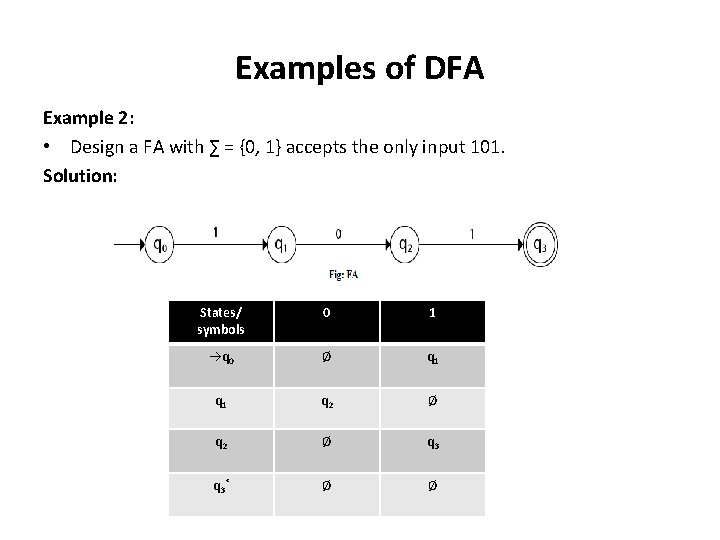
Examples of DFA Example 2: • Design a FA with ∑ = {0, 1} accepts the only input 101. Solution: States/ symbols 0 1 q 0 Ø q 1 q 2 Ø q 3* Ø Ø

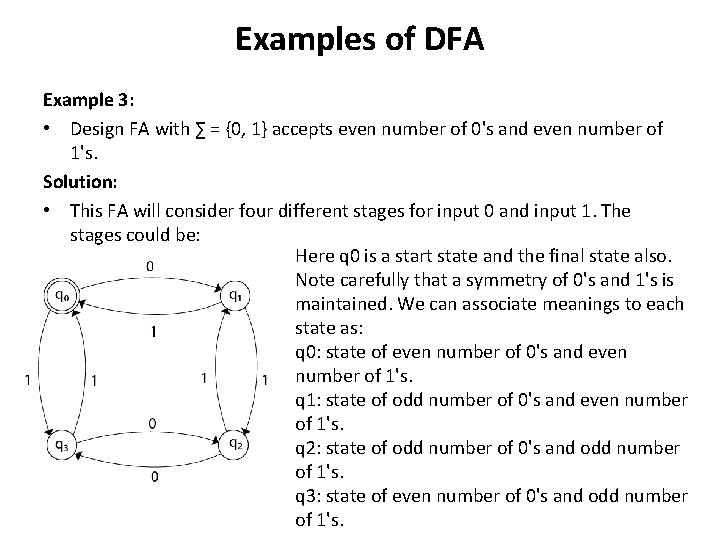
Examples of DFA Example 3: • Design FA with ∑ = {0, 1} accepts even number of 0's and even number of 1's. Solution: • This FA will consider four different stages for input 0 and input 1. The stages could be: Here q 0 is a start state and the final state also. Note carefully that a symmetry of 0's and 1's is maintained. We can associate meanings to each state as: q 0: state of even number of 0's and even number of 1's. q 1: state of odd number of 0's and even number of 1's. q 2: state of odd number of 0's and odd number of 1's. q 3: state of even number of 0's and odd number of 1's.

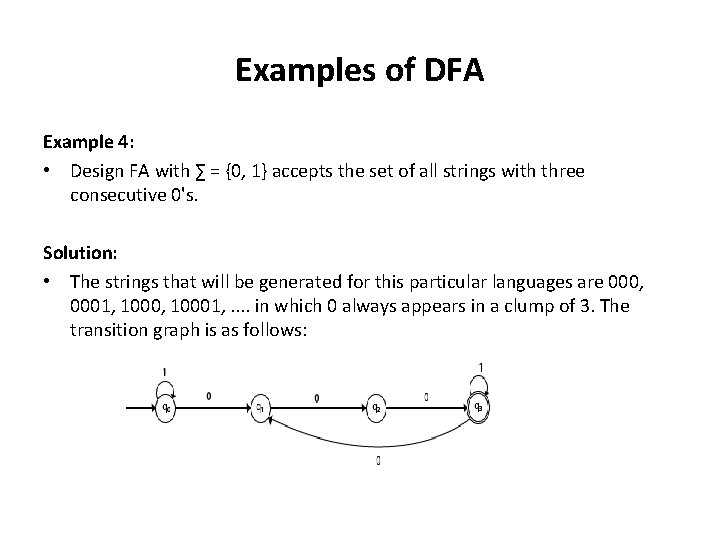
Examples of DFA Example 4: • Design FA with ∑ = {0, 1} accepts the set of all strings with three consecutive 0's. Solution: • The strings that will be generated for this particular languages are 000, 0001, 10001, . . in which 0 always appears in a clump of 3. The transition graph is as follows:

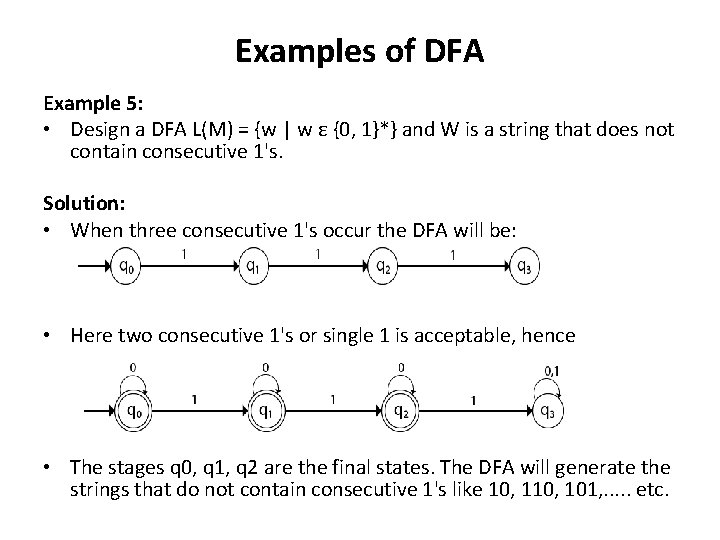
Examples of DFA Example 5: • Design a DFA L(M) = {w | w ε {0, 1}*} and W is a string that does not contain consecutive 1's. Solution: • When three consecutive 1's occur the DFA will be: • Here two consecutive 1's or single 1 is acceptable, hence • The stages q 0, q 1, q 2 are the final states. The DFA will generate the strings that do not contain consecutive 1's like 10, 101, . . . etc.

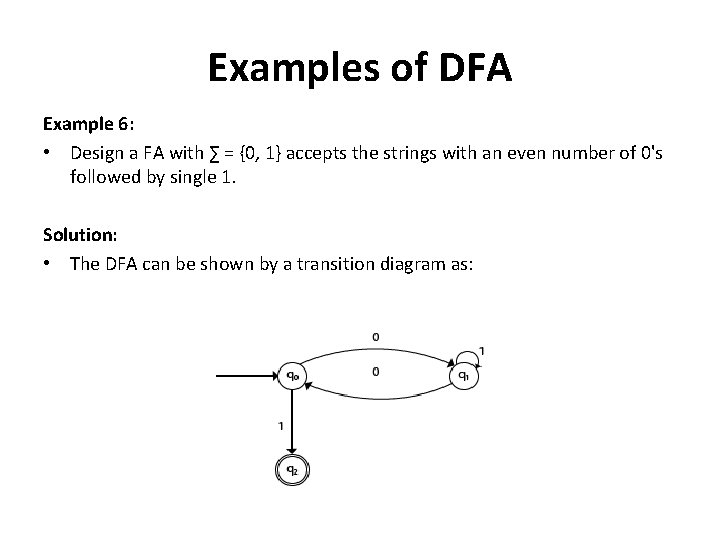
Examples of DFA Example 6: • Design a FA with ∑ = {0, 1} accepts the strings with an even number of 0's followed by single 1. Solution: • The DFA can be shown by a transition diagram as:

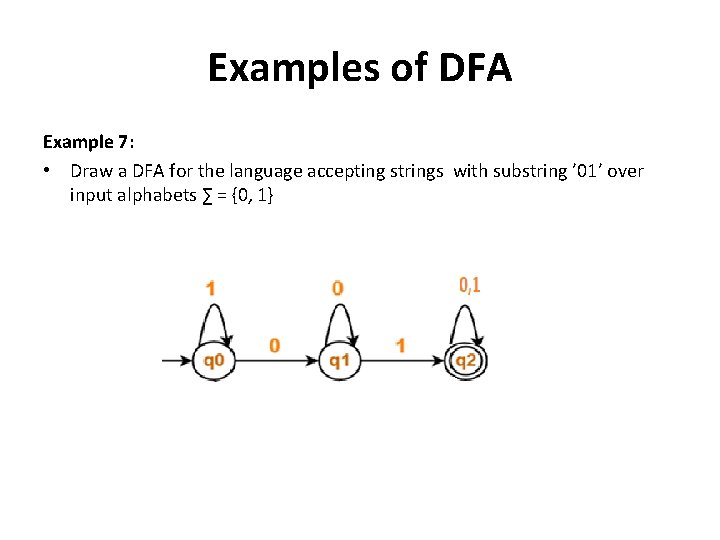
Examples of DFA Example 7: • Draw a DFA for the language accepting strings with substring ’ 01’ over input alphabets ∑ = {0, 1}

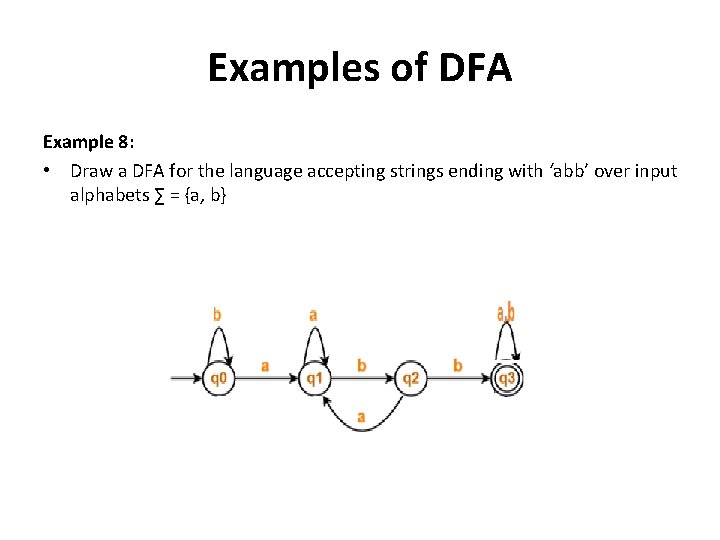
Examples of DFA Example 8: • Draw a DFA for the language accepting strings ending with ‘abb’ over input alphabets ∑ = {a, b}

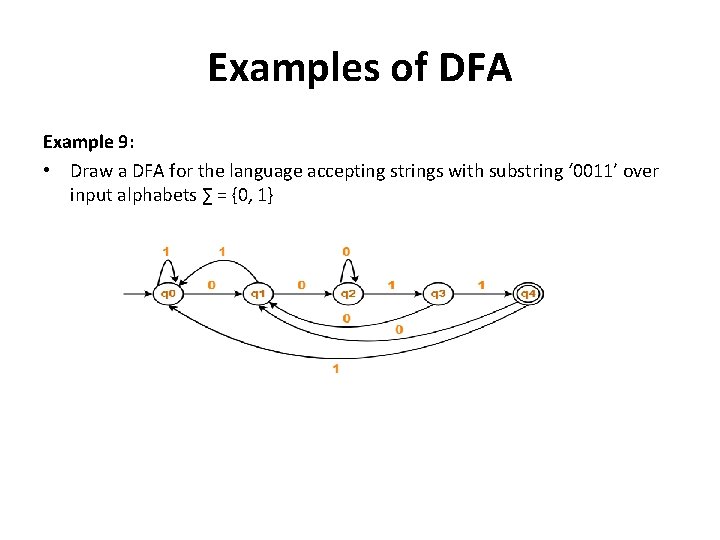
Examples of DFA Example 9: • Draw a DFA for the language accepting strings with substring ‘ 0011’ over input alphabets ∑ = {0, 1}

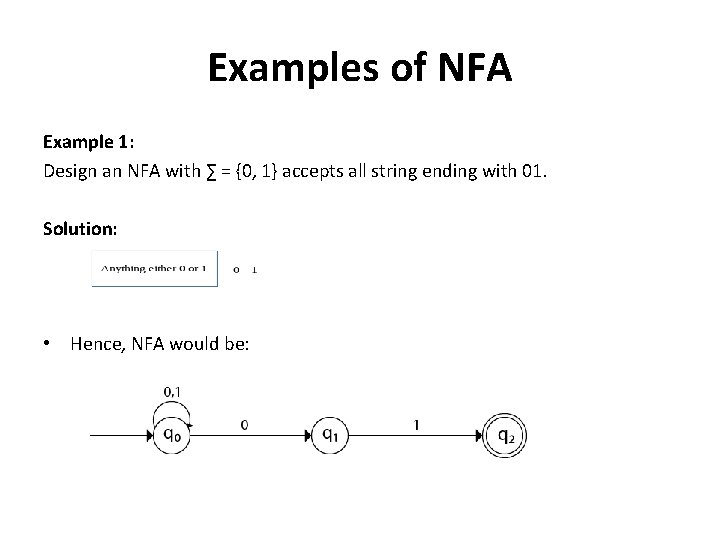
Examples of NFA Example 1: Design an NFA with ∑ = {0, 1} accepts all string ending with 01. Solution: • Hence, NFA would be:

Examples of NFA Example 2: Design an NFA with ∑ = {0, 1} in which double '1' is followed by double '0'. Solution: • Now before double 1, there can be any string of 0 and 1. Similarly, after double 0, there can be any string of 0 and 1. • Hence the NFA becomes:

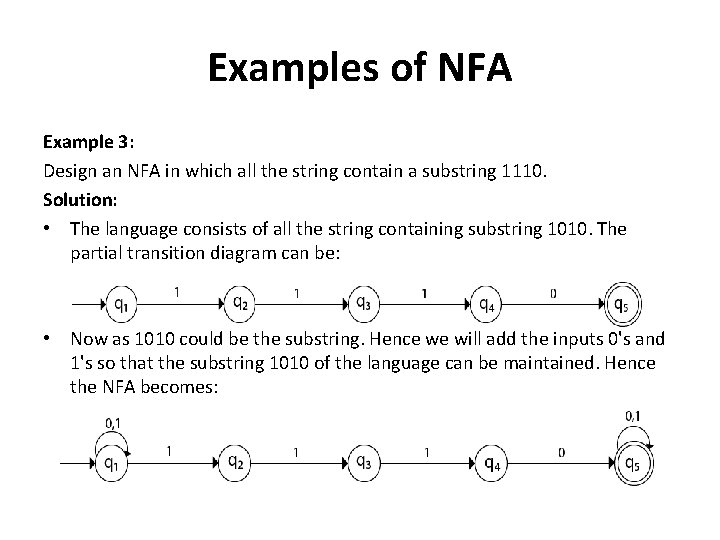
Examples of NFA Example 3: Design an NFA in which all the string contain a substring 1110. Solution: • The language consists of all the string containing substring 1010. The partial transition diagram can be: • Now as 1010 could be the substring. Hence we will add the inputs 0's and 1's so that the substring 1010 of the language can be maintained. Hence the NFA becomes:

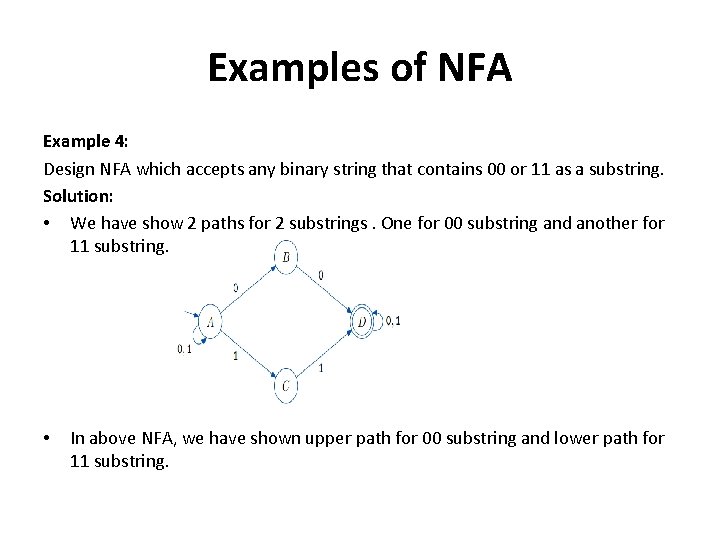
Examples of NFA Example 4: Design NFA which accepts any binary string that contains 00 or 11 as a substring. Solution: • We have show 2 paths for 2 substrings. One for 00 substring and another for 11 substring. • In above NFA, we have shown upper path for 00 substring and lower path for 11 substring.

Converting NFA to DFA The following steps are followed to convert a given NFA to a DFAStep 1: • Let Q’ be a new set of states of the DFA. Q’ is null in the starting. • Let T’ be a new transition table of the DFA. Step 2: • Add start state of the NFA to Q’. • Add transitions of the start state to the transition table T’. • If start state makes transition to multiple states for some input alphabet, then treat those multiple states as a single state in the DFA. • In NFA, if the transition of start state over some input alphabet is null, then perform the transition of start state over that input alphabet to a dead state in the DFA. Step 3: • If any new state is present in the transition table T’, • Add the new state in Q’. • Add transitions of that state in the transition table T’. Step 4: • Keep repeating Step 3 until no new state is present in the transition table T’. • Finally, the transition table T’ so obtained is the complete transition table of the required DFA.

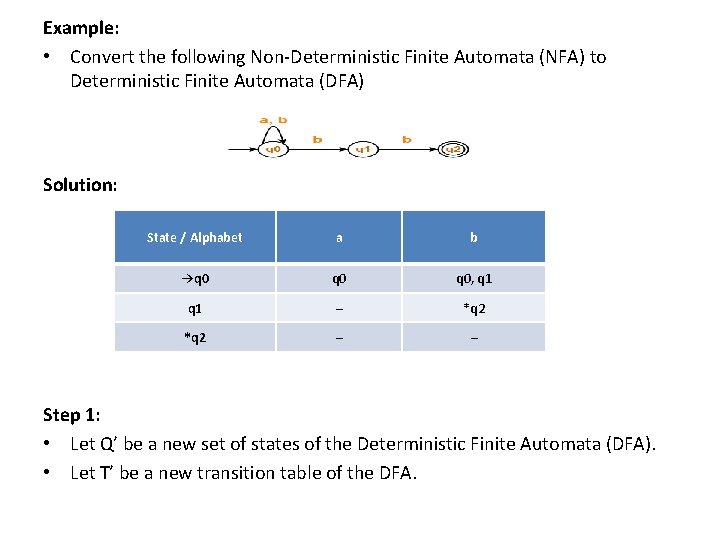
Example: • Convert the following Non-Deterministic Finite Automata (NFA) to Deterministic Finite Automata (DFA) Solution: State / Alphabet a b →q 0 q 0, q 1 – *q 2 – – Step 1: • Let Q’ be a new set of states of the Deterministic Finite Automata (DFA). • Let T’ be a new transition table of the DFA.

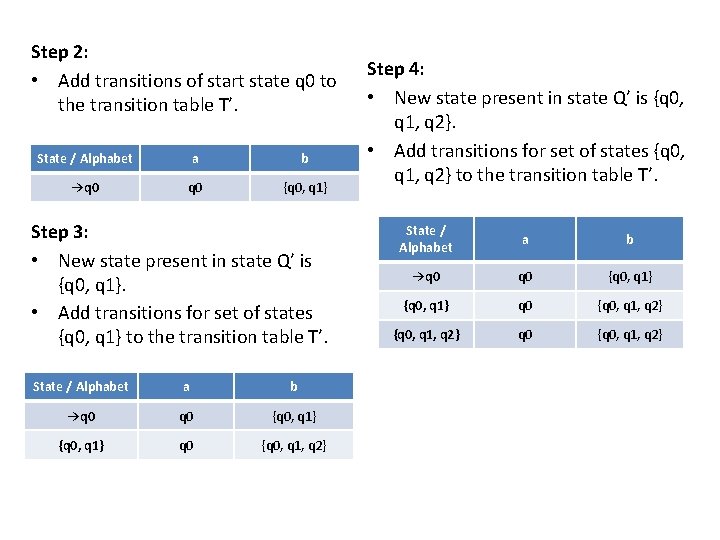
Step 2: • Add transitions of start state q 0 to the transition table T’. State / Alphabet a b →q 0 {q 0, q 1} Step 3: • New state present in state Q’ is {q 0, q 1}. • Add transitions for set of states {q 0, q 1} to the transition table T’. State / Alphabet a b →q 0 {q 0, q 1} q 0 {q 0, q 1, q 2} Step 4: • New state present in state Q’ is {q 0, q 1, q 2}. • Add transitions for set of states {q 0, q 1, q 2} to the transition table T’. State / Alphabet a b →q 0 {q 0, q 1} q 0 {q 0, q 1, q 2}

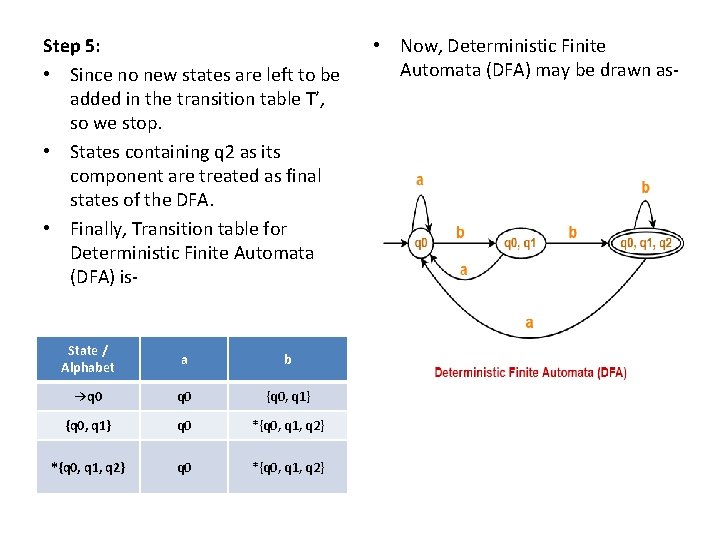
Step 5: • Since no new states are left to be added in the transition table T’, so we stop. • States containing q 2 as its component are treated as final states of the DFA. • Finally, Transition table for Deterministic Finite Automata (DFA) is- State / Alphabet a b →q 0 {q 0, q 1} q 0 *{q 0, q 1, q 2} • Now, Deterministic Finite Automata (DFA) may be drawn as-

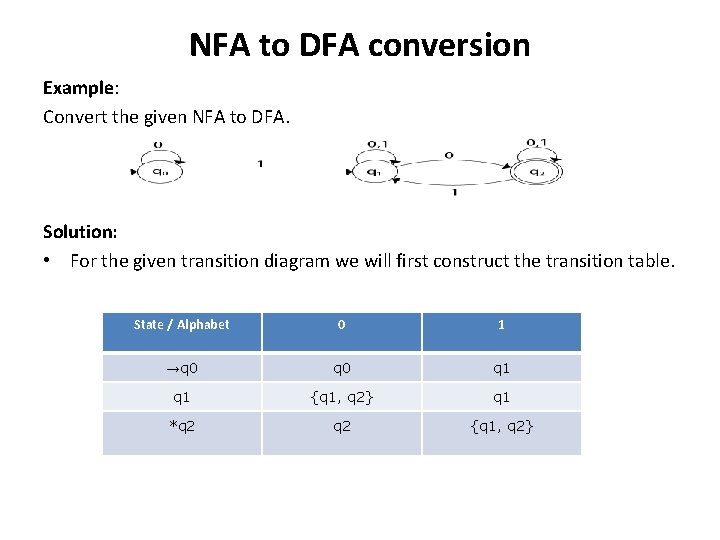
NFA to DFA conversion Example: Convert the given NFA to DFA. Solution: • For the given transition diagram we will first construct the transition table. State / Alphabet 0 1 →q 0 q 1 {q 1, q 2} q 1 *q 2 {q 1, q 2}

• Transition table for DFA is State / Alphabet 0 1 →[q 0] [q 1] [q 1, q 2] [q 1] *[q 2] [q 1, q 2] *[q 1, q 2] • The Transition diagram will be:

NFA with ε • Non-deterministic finite automata(NFA) is a finite automata where for some cases when a specific input is given to the current state, the machine goes to multiple states or more than 1 states. • It can contain ε move. • It can be represented as M = { Q, ∑, δ, q 0, F}. Where § Q: finite set of states § ∑: finite set of the input symbol § q 0: initial state § F: final state § δ: Transition function • NFA with ∈ move: If any FA contains ε transaction or move, the finite automata is called NFA with ∈ move. • ε-closure: ε-closure for a given state A means a set of states which can be reached from the state A with only ε(null) move including the state A itself.

Steps for converting NFA with ε to DFA: • Step 1: We will take the ε-closure for the starting state of NFA as a starting state of DFA. • Step 2: Find the states for each input symbol that can be traversed from the present. That means the union of transition value and their closures for each state of NFA present in the current state of DFA. • Step 3: If we found a new state, take it as current state and repeat step 2. • Step 4: Repeat Step 2 and Step 3 until there is no new state present in the transition table of DFA. • Step 5: Mark the states of DFA as a final state which contains the final state of NFA.

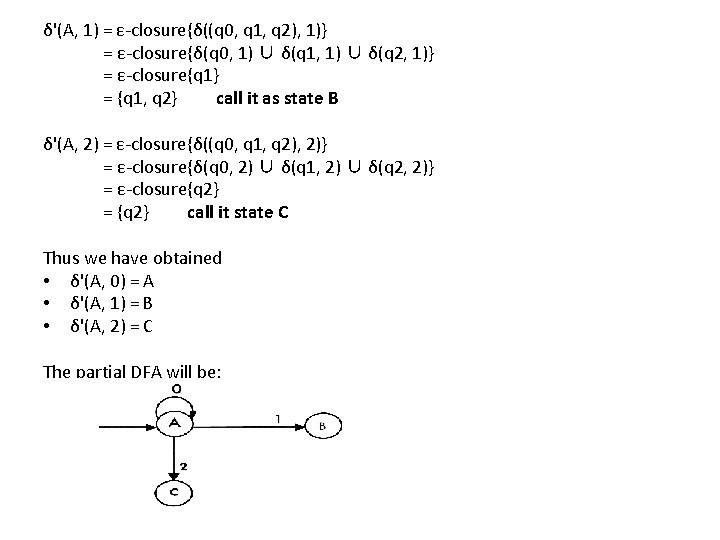
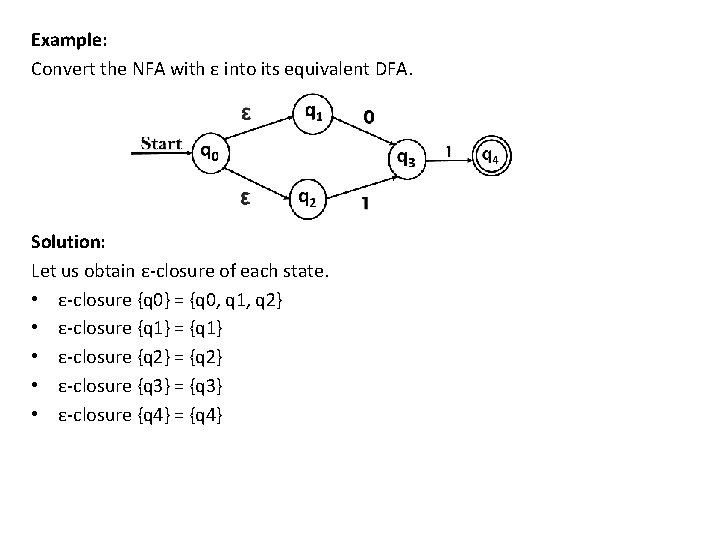
Example 1: Convert the given NFA into its equivalent DFA. Solution: Let us obtain the ε-closure of each state. • ε-closure(q 0) = {q 0, q 1, q 2} • ε-closure(q 1) = {q 1, q 2} • ε-closure(q 2) = {q 2} Now we will obtain δ' transition. Let ε-closure(q 0) = {q 0, q 1, q 2} call it as state A. δ'(A, 0) = ε-closure{δ((q 0, q 1, q 2), 0)} = ε-closure{δ(q 0, 0) ∪ δ(q 1, 0) ∪ δ(q 2, 0)} = ε-closure{q 0} = {q 0, q 1, q 2}

δ'(A, 1) = ε-closure{δ((q 0, q 1, q 2), 1)} = ε-closure{δ(q 0, 1) ∪ δ(q 1, 1) ∪ δ(q 2, 1)} = ε-closure{q 1} = {q 1, q 2} call it as state B δ'(A, 2) = ε-closure{δ((q 0, q 1, q 2), 2)} = ε-closure{δ(q 0, 2) ∪ δ(q 1, 2) ∪ δ(q 2, 2)} = ε-closure{q 2} = {q 2} call it state C Thus we have obtained • δ'(A, 0) = A • δ'(A, 1) = B • δ'(A, 2) = C The partial DFA will be:

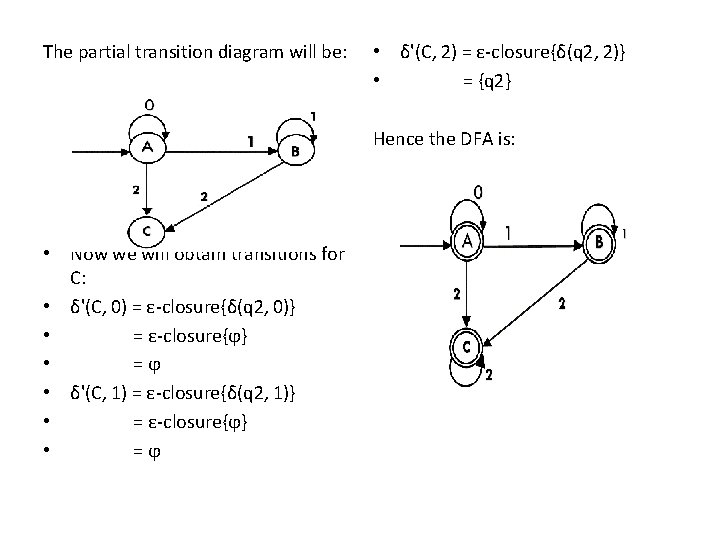
Now we will find the transitions on states B and C for each input. Hence δ'(B, 0) = ε-closure{δ((q 1, q 2), 0)} = ε-closure{δ(q 1, 0) ∪ δ(q 2, 0)} = ε-closure{ϕ} = ϕ δ'(B, 1) = ε-closure{δ((q 1, q 2), 1)} = ε-closure{δ(q 1, 1) ∪ δ(q 2, 1)} = ε-closure{q 1} = {q 1, q 2} i. e. state B itself δ'(B, 2) = ε-closure{δ((q 1, q 2), 2)} = ε-closure{δ(q 1, 2) ∪ δ(q 2, 2)} = ε-closure{q 2} = {q 2} i. e. state C itself Thus we have obtained • δ'(B, 0) = ϕ • δ'(B, 1) = B • δ'(B, 2) = C

The partial transition diagram will be: • δ'(C, 2) = ε-closure{δ(q 2, 2)} • = {q 2} Hence the DFA is: • Now we will obtain transitions for C: • δ'(C, 0) = ε-closure{δ(q 2, 0)} • = ε-closure{ϕ} • =ϕ • δ'(C, 1) = ε-closure{δ(q 2, 1)} • = ε-closure{ϕ} • =ϕ

Example: Convert the NFA with ε into its equivalent DFA. Solution: Let us obtain ε-closure of each state. • ε-closure {q 0} = {q 0, q 1, q 2} • ε-closure {q 1} = {q 1} • ε-closure {q 2} = {q 2} • ε-closure {q 3} = {q 3} • ε-closure {q 4} = {q 4}

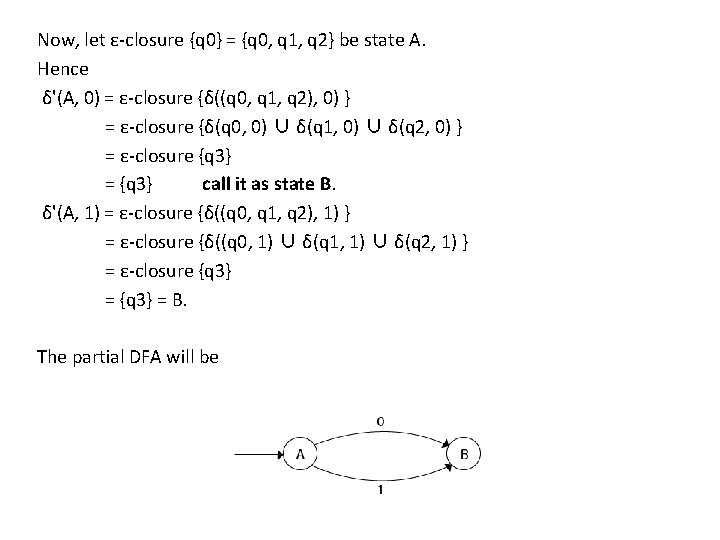
Now, let ε-closure {q 0} = {q 0, q 1, q 2} be state A. Hence δ'(A, 0) = ε-closure {δ((q 0, q 1, q 2), 0) } = ε-closure {δ(q 0, 0) ∪ δ(q 1, 0) ∪ δ(q 2, 0) } = ε-closure {q 3} = {q 3} call it as state B. δ'(A, 1) = ε-closure {δ((q 0, q 1, q 2), 1) } = ε-closure {δ((q 0, 1) ∪ δ(q 1, 1) ∪ δ(q 2, 1) } = ε-closure {q 3} = B. The partial DFA will be

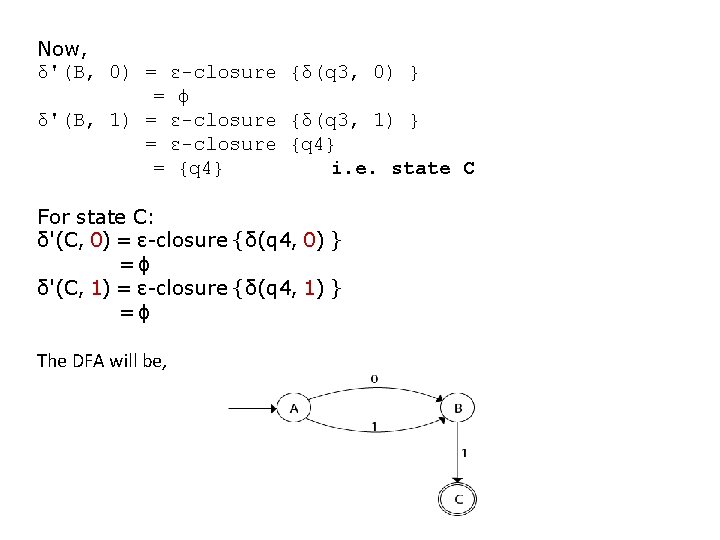
Now, δ'(B, 0) = ε-closure {δ(q 3, 0) } = ϕ δ'(B, 1) = ε-closure {δ(q 3, 1) } = ε-closure {q 4} = {q 4} i. e. state C For state C: δ'(C, 0) = ε-closure {δ(q 4, 0) } =ϕ δ'(C, 1) = ε-closure {δ(q 4, 1) } =ϕ The DFA will be,

Minimization of DFA • Minimization of DFA means reducing the number of states from given FA. Thus, we get the FSM(finite state machine) with redundant states after minimizing the FSM. • We have to follow the various steps to minimize the DFA. These are as follows: • Step 1: Remove all the states that are unreachable from the initial state via any set of the transition of DFA. • Step 2: Draw the transition table for all pair of states. • Step 3: Now split the transition table into two tables T 1 and T 2. T 1 contains all final states, and T 2 contains non-final states. • Step 4: Find similar rows from T 1 such that: 1. δ (q, a) = p 2. δ (r, a) = p • That means, find the two states which have the same value of a and b and remove one of them. • Step 5: Repeat step 3 until we find no similar rows available in the transition table T 1. • Step 6: Repeat step 3 and step 4 for table T 2 also. • Step 7: Now combine the reduced T 1 and T 2 tables. The combined transition table is the transition table of minimized DFA.

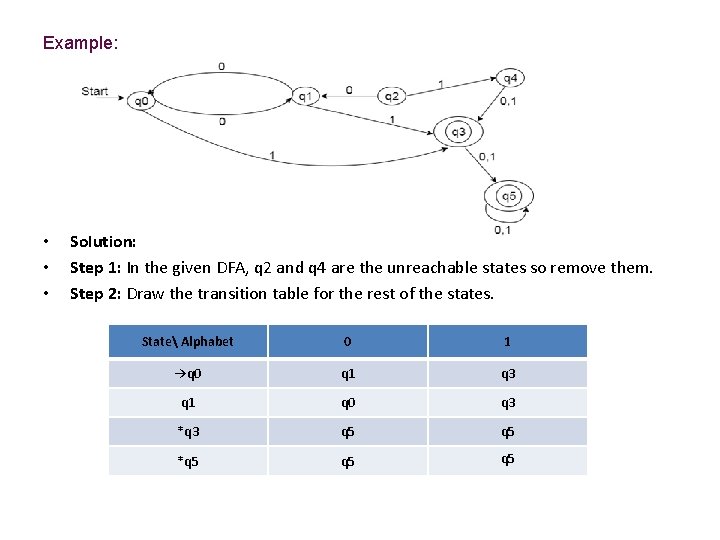
Example: • • • Solution: Step 1: In the given DFA, q 2 and q 4 are the unreachable states so remove them. Step 2: Draw the transition table for the rest of the states. State Alphabet 0 1 →q 0 q 1 q 3 q 1 q 0 q 3 *q 3 q 5 *q 5 q 5

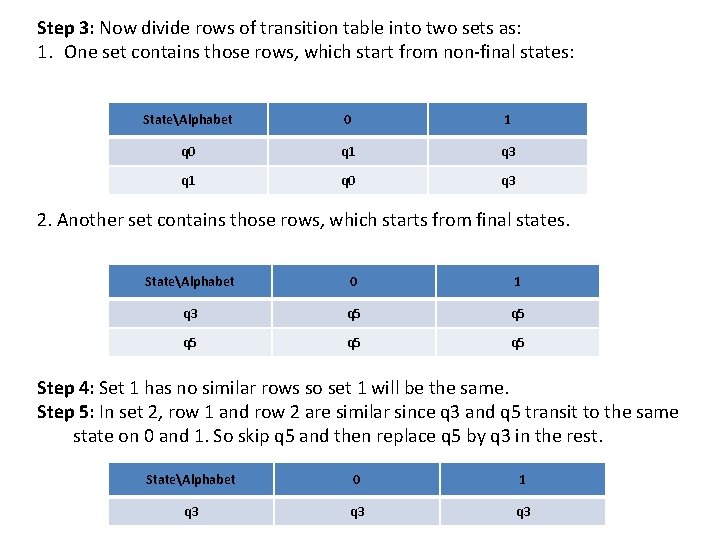
Step 3: Now divide rows of transition table into two sets as: 1. One set contains those rows, which start from non-final states: StateAlphabet 0 1 q 0 q 1 q 3 q 1 q 0 q 3 2. Another set contains those rows, which starts from final states. StateAlphabet 0 1 q 3 q 5 q 5 q 5 Step 4: Set 1 has no similar rows so set 1 will be the same. Step 5: In set 2, row 1 and row 2 are similar since q 3 and q 5 transit to the same state on 0 and 1. So skip q 5 and then replace q 5 by q 3 in the rest. StateAlphabet 0 1 q 3 q 3

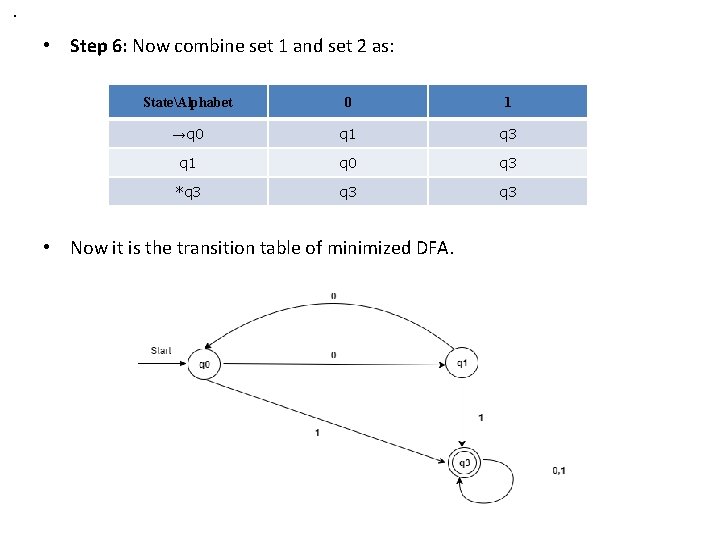
. • Step 6: Now combine set 1 and set 2 as: StateAlphabet 0 1 →q 0 q 1 q 3 q 1 q 0 q 3 *q 3 q 3 • Now it is the transition table of minimized DFA.

Moore Machine • Moore machine is a finite state machine in which the next state is decided by the current state and current input symbol. • The output symbol at a given time depends only on the present state of the machine. • Moore machine can be described by 6 tuples (Q, q 0, ∑, O, δ, λ) where • Q: finite set of states • q 0: initial state of machine • ∑: finite set of input symbols • O: output alphabet • δ: transition function where Q × ∑ → Q • λ: output function where Q → O

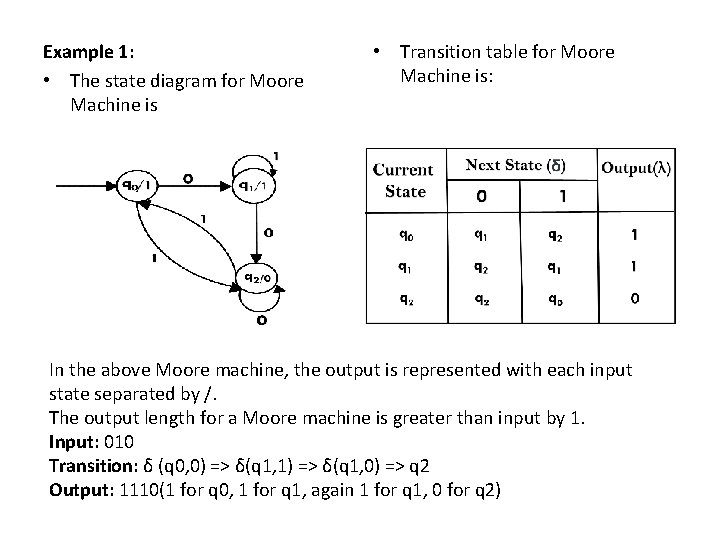
Example 1: • The state diagram for Moore Machine is • Transition table for Moore Machine is: In the above Moore machine, the output is represented with each input state separated by /. The output length for a Moore machine is greater than input by 1. Input: 010 Transition: δ (q 0, 0) => δ(q 1, 1) => δ(q 1, 0) => q 2 Output: 1110(1 for q 0, 1 for q 1, again 1 for q 1, 0 for q 2)

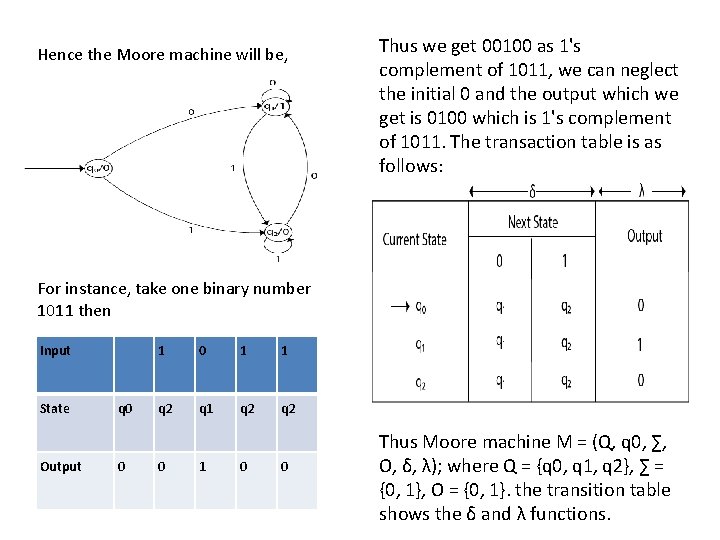
Example 2: • Design a Moore machine to generate 1's complement of a given binary number. Solution: • To generate 1's complement of a given binary number the simple logic is that if the input is 0 then the output will be 1 and if the input is 1 then the output will be 0. • That means there are three states. One state is start state. The second state is for taking 0's as input and produces output as 1. The third state is for taking 1's as input and producing output as 0.

Hence the Moore machine will be, Thus we get 00100 as 1's complement of 1011, we can neglect the initial 0 and the output which we get is 0100 which is 1's complement of 1011. The transaction table is as follows: For instance, take one binary number 1011 then Input State Output q 0 0 1 1 q 2 q 2 0 1 0 0 Thus Moore machine M = (Q, q 0, ∑, O, δ, λ); where Q = {q 0, q 1, q 2}, ∑ = {0, 1}, O = {0, 1}. the transition table shows the δ and λ functions.

Example 3: • Construct a Moore machine that determines whether an input string contains an even or odd number of 1's. The machine should give 1 as output if an even number of 1's are in the string and 0 otherwise. Solution: • The Moore machine will be: • This is the required Moore machine. In this machine, state q 1 accepts an odd number of 1's and state q 0 accepts even number of 1's. There is no restriction on a number of zeros. Hence for 0 input, self-loop can be applied on both the states.

Mealy Machine • A Mealy machine is a machine in which output symbol depends upon the present input symbol and present state of the machine. In the Mealy machine, the output is represented with each input symbol for each state separated by /. The Mealy machine can be described by 6 tuples (Q, q 0, ∑, O, δ, λ') where • Q: finite set of states • q 0: initial state of machine • ∑: finite set of input alphabet • O: output alphabet • δ: transition function where Q × ∑ → Q • λ': output function where Q × ∑ →O

Example: Design a mealy machine to find 2’s complement of given number Solution: • 2’s complement of a given number can be found by changing bits from right end till the first 1 and then complementing the remaining bits. • E. g. 2’s complement of binary number 0101101000 is calculated as 0 1 1 0 0 0 1 1 0 0 0

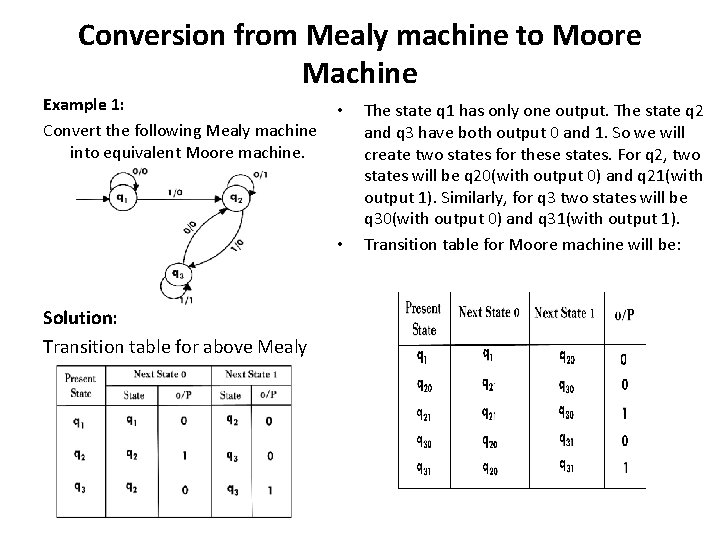
Conversion from Mealy machine to Moore Machine Example 1: Convert the following Mealy machine into equivalent Moore machine. • • Solution: Transition table for above Mealy machine is as follows: The state q 1 has only one output. The state q 2 and q 3 have both output 0 and 1. So we will create two states for these states. For q 2, two states will be q 20(with output 0) and q 21(with output 1). Similarly, for q 3 two states will be q 30(with output 0) and q 31(with output 1). Transition table for Moore machine will be:

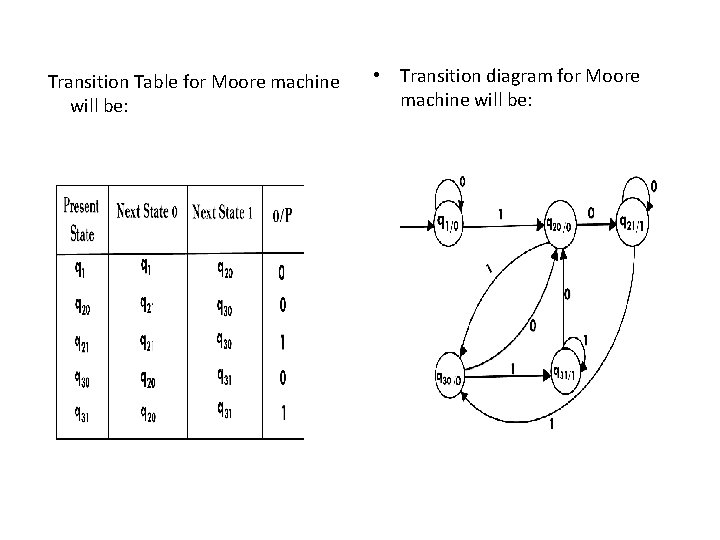
Transition Table for Moore machine will be: • Transition diagram for Moore machine will be:

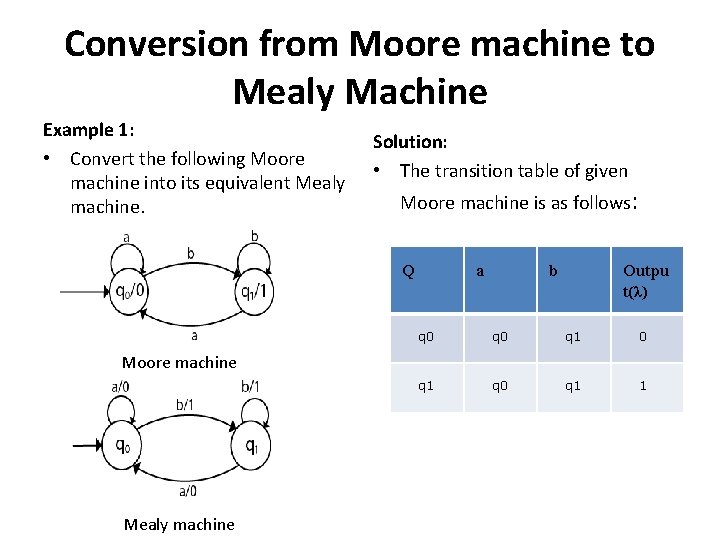
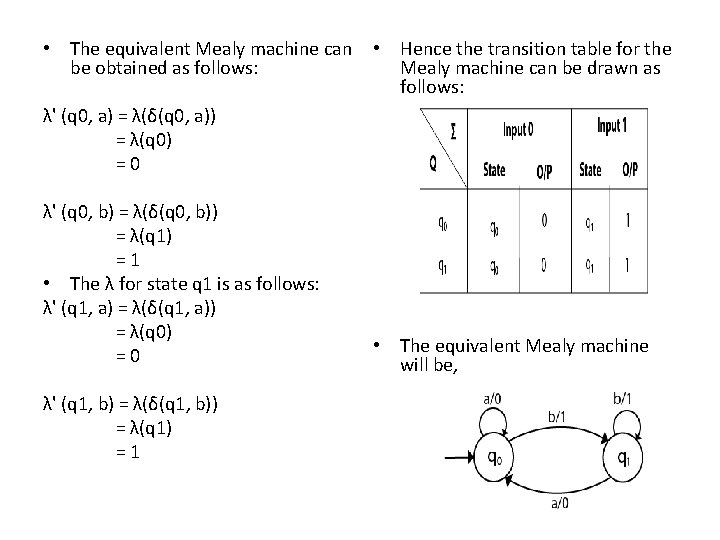
Conversion from Moore machine to Mealy Machine Example 1: • Convert the following Moore machine into its equivalent Mealy machine. Solution: • The transition table of given Moore machine is as follows: Q a b Outpu t(λ) q 0 q 1 q 0 q 1 1 Moore machine Mealy machine

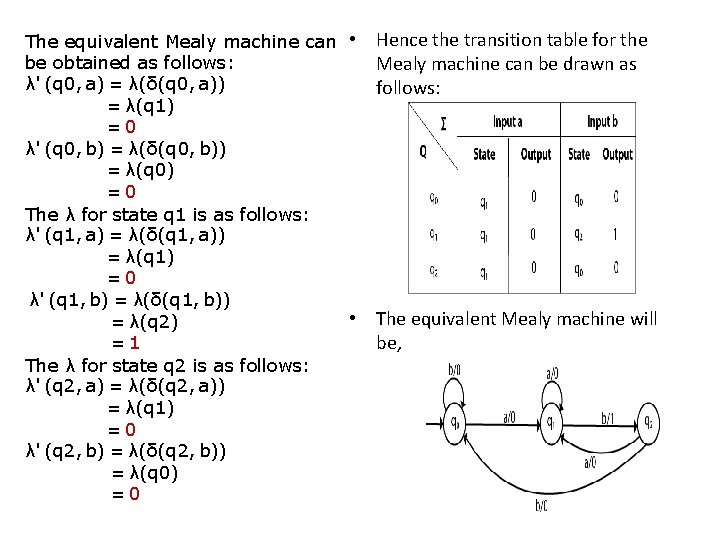
• The equivalent Mealy machine can be obtained as follows: • Hence the transition table for the Mealy machine can be drawn as follows: λ' (q 0, a) = λ(δ(q 0, a)) = λ(q 0) =0 λ' (q 0, b) = λ(δ(q 0, b)) = λ(q 1) =1 • The λ for state q 1 is as follows: λ' (q 1, a) = λ(δ(q 1, a)) = λ(q 0) =0 λ' (q 1, b) = λ(δ(q 1, b)) = λ(q 1) =1 • The equivalent Mealy machine will be,

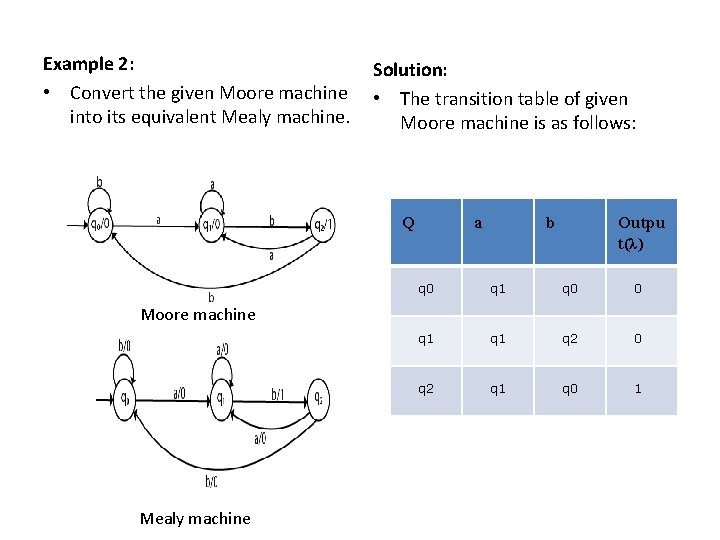
Example 2: • Convert the given Moore machine into its equivalent Mealy machine. Solution: • The transition table of given Moore machine is as follows: Q a b Outpu t(λ) q 0 q 1 q 0 0 q 1 q 2 0 q 2 q 1 q 0 1 Moore machine Mealy machine

The equivalent Mealy machine can • be obtained as follows: λ' (q 0, a) = λ(δ(q 0, a)) = λ(q 1) =0 λ' (q 0, b) = λ(δ(q 0, b)) = λ(q 0) =0 The λ for state q 1 is as follows: λ' (q 1, a) = λ(δ(q 1, a)) = λ(q 1) =0 λ' (q 1, b) = λ(δ(q 1, b)) • = λ(q 2) =1 The λ for state q 2 is as follows: λ' (q 2, a) = λ(δ(q 2, a)) = λ(q 1) =0 λ' (q 2, b) = λ(δ(q 2, b)) = λ(q 0) =0 Hence the transition table for the Mealy machine can be drawn as follows: The equivalent Mealy machine will be,

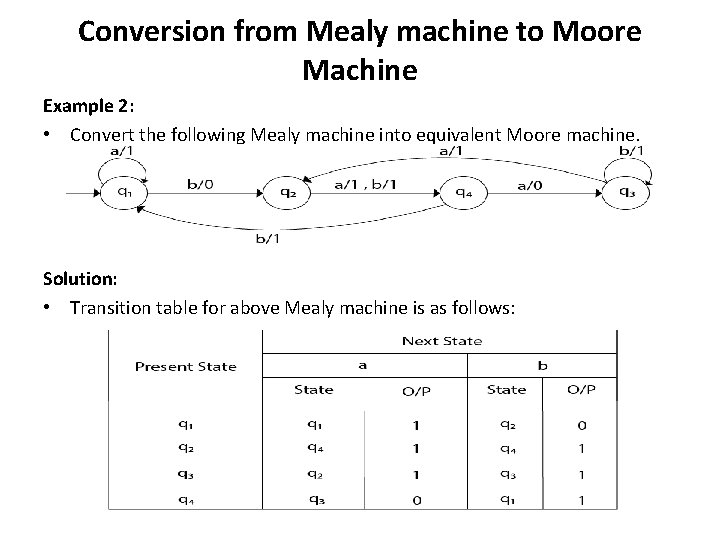
Conversion from Mealy machine to Moore Machine Example 2: • Convert the following Mealy machine into equivalent Moore machine. Solution: • Transition table for above Mealy machine is as follows:

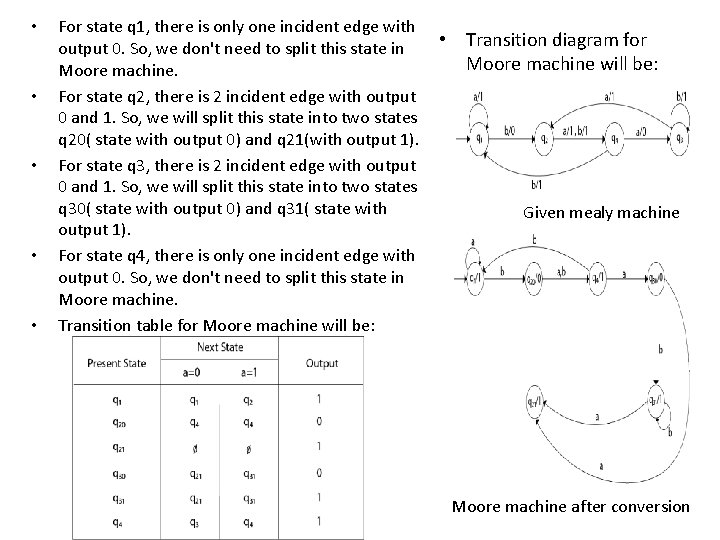
• • • For state q 1, there is only one incident edge with output 0. So, we don't need to split this state in Moore machine. For state q 2, there is 2 incident edge with output 0 and 1. So, we will split this state into two states q 20( state with output 0) and q 21(with output 1). For state q 3, there is 2 incident edge with output 0 and 1. So, we will split this state into two states q 30( state with output 0) and q 31( state with output 1). For state q 4, there is only one incident edge with output 0. So, we don't need to split this state in Moore machine. Transition table for Moore machine will be: • Transition diagram for Moore machine will be: Given mealy machine Moore machine after conversion

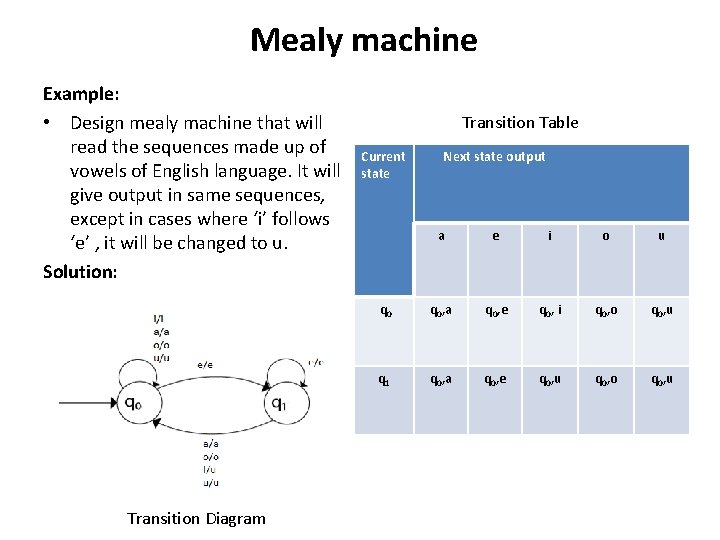
Mealy machine Example: • Design mealy machine that will read the sequences made up of vowels of English language. It will give output in same sequences, except in cases where ‘i’ follows ‘e’ , it will be changed to u. Solution: S Transition Diagram Transition Table Current state Next state output a e i o u q 0, a q 0, e q 0, i q 0, o q 0, u q 1 q 0, a q 0, e q 0, u q 0, o q 0, u

Difference Between Moore and Mealy Machine • • Moore Machine – Output depends only upon present state. If input changes, output does not change. More number of states are required. There is less hardware requirement for circuit implementation. They react faster to inputs. Synchronous output and state generation. Output is placed on states. Easy to design. • • Mealy Machine – Output depends on present state as well as present input. If input changes, output also changes. Less number of states are required. There is more hardware requirement for circuit implementation. They react slower to inputs(One clock cycle later). Asynchronous output generation. Output is placed on transitions. It is difficult to design.

Difference between DFA and NFA • DFA stands for Deterministic • Finite Automata. • DFA cannot use Empty • String transition. • DFA can be understood as • one machine. • DFA is more difficult to construct. • • Time needed for executing • an Input string is less. • All DFA are NFA. • NFA stands for Nondeterministic Finite Automata. NFA can use Empty String transition. NFA can be understood as multiple little machines computing at the same time. NFA is easier to construct. Time needed for executing an input string is more. Not all NFA are DFA.