Finite Element Method in Geotechnical Engineering Short Course

Finite Element Method in Geotechnical Engineering Short Course on Computational Geotechnics + Dynamics Boulder, Colorado January 5 -8, 2004 Stein Sture Professor of Civil Engineering University of Colorado at Boulder

Contents n n n n n Steps in the FE Method Introduction to FEM for Deformation Analysis Discretization of a Continuum Elements Strains Stresses, Constitutive Relations Hooke’s Law Formulation of Stiffness Matrix Solution of Equations Computational Geotechnics Finite Element Method in Geotechnical Engineering

Steps in the FE Method 1. Establishment of stiffness relations for each element. Material properties and equilibrium conditions for each element are used in this establishment. 2. Enforcement of compatibility, i. e. the elements are connected. 3. Enforcement of equilibrium conditions for the whole structure, in the present case for the nodal points. 4. By means of 2. And 3. the system of equations is constructed for the whole structure. This step is called assembling. 5. In order to solve the system of equations for the whole structure, the boundary conditions are enforced. 6. Solution of the system of equations. Computational Geotechnics Finite Element Method in Geotechnical Engineering

Introduction to FEM for Deformation Analysis n General method to solve boundary value problems in an approximate and discretized way n Often (but not only) used for deformation and stress analysis n Division of geometry into finite element mesh Computational Geotechnics Finite Element Method in Geotechnical Engineering

Introduction to FEM for Deformation Analysis n n n Pre-assumed interpolation of main quantities (displacements) over elements, based on values in points (nodes) Formation of (stiffness) matrix, K, and (force) vector, r Global solution of main quantities in nodes, d d D KD=R r R k K Computational Geotechnics Finite Element Method in Geotechnical Engineering

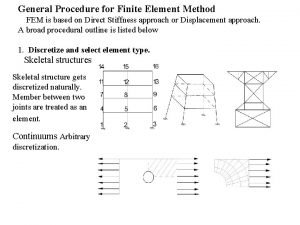
Discretization of a Continuum n 2 D modeling: Computational Geotechnics Finite Element Method in Geotechnical Engineering

Discretization of a Continuum n 2 D cross section is divided into element: Several element types are possible (triangles and quadrilaterals) Computational Geotechnics Finite Element Method in Geotechnical Engineering

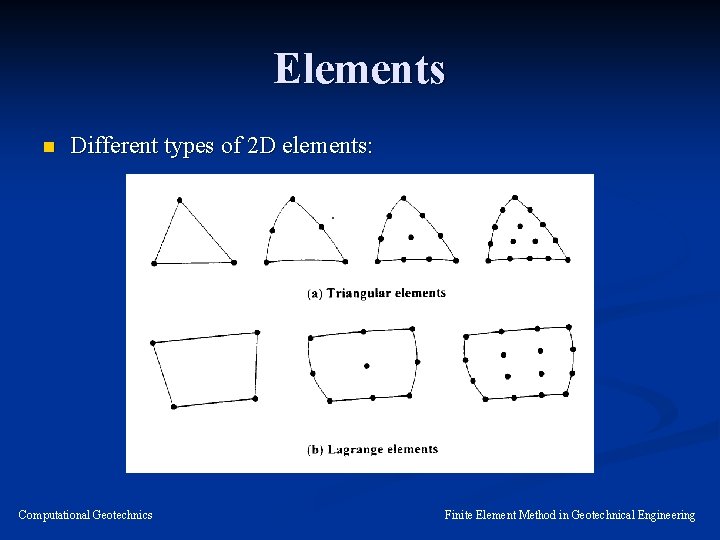
Elements n Different types of 2 D elements: Computational Geotechnics Finite Element Method in Geotechnical Engineering

Elements Example: Other way of writing: ux = N 1 ux 1 + N 2 ux 2 + N 3 ux 3 + N 4 ux 4 + N 5 ux 5 + N 6 ux 6 uy = N 1 uy 1 + N 2 uy 2 + N 3 uy 3 + N 4 uy 4 + N 5 uy 5 + N 6 uy 6 or ux = N ux and uy = N uy (N contains functions of x and y) Computational Geotechnics Finite Element Method in Geotechnical Engineering

Strains are the derivatives of displacements. In finite elements they are determined from the derivatives of the interpolation functions: or (strains composed in a vector and matrix B contains derivatives of N ) Computational Geotechnics Finite Element Method in Geotechnical Engineering

Stresses, Constitutive Relations Cartesian stress tensor, usually composed in a vector: Stresses, s, are related to strains e: s = Ce In fact, the above relationship is used in incremental form: C is material stiffness matrix and determining material behavior Computational Geotechnics Finite Element Method in Geotechnical Engineering

Hooke’s Law For simple linear elastic behavior C is based on Hooke’s law: Computational Geotechnics Finite Element Method in Geotechnical Engineering

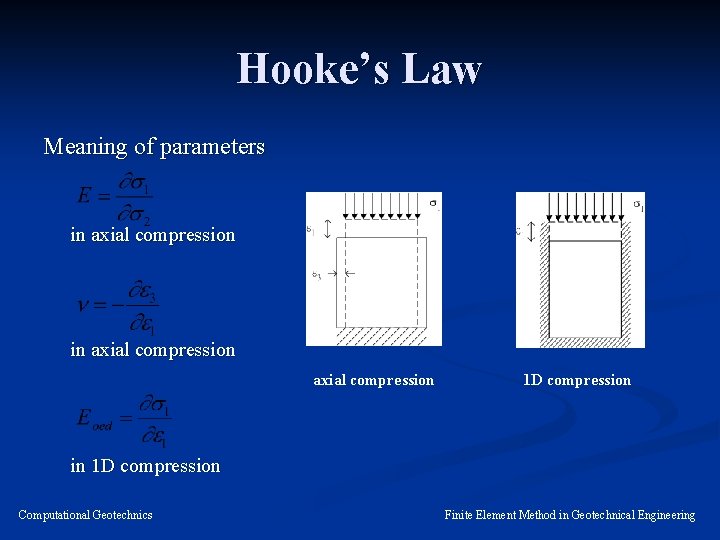
Hooke’s Law Basic parameters in Hooke’s law: Young’s modulus E Poisson’s ratio Auxiliary parameters, related to basic parameters: Shear modulus Oedometer modulus Bulk modulus Computational Geotechnics Finite Element Method in Geotechnical Engineering

Hooke’s Law Meaning of parameters in axial compression 1 D compression in 1 D compression Computational Geotechnics Finite Element Method in Geotechnical Engineering

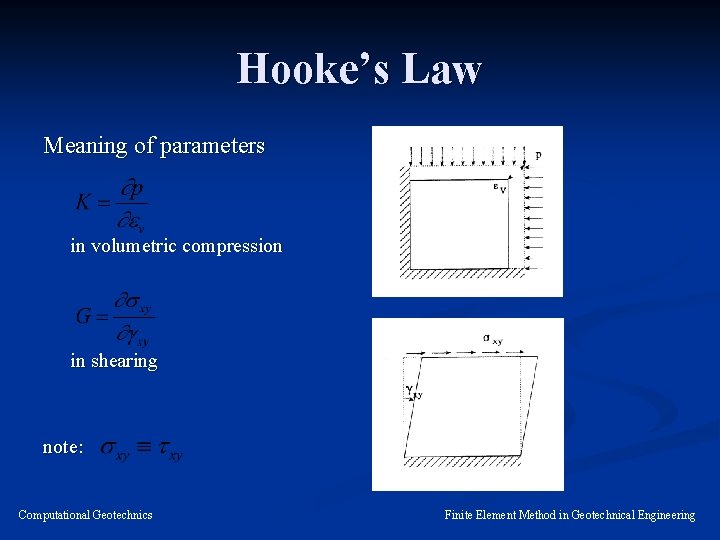
Hooke’s Law Meaning of parameters in volumetric compression in shearing note: Computational Geotechnics Finite Element Method in Geotechnical Engineering

Hooke’s Law Summary, Hooke’s law:

Hooke’s Law Inverse relationship: Computational Geotechnics Finite Element Method in Geotechnical Engineering

Formulation of Stiffness Matrix Formation of element stiffness matrix Ke Integration is usually performed numerically: Gauss integration (summation over sample points) coefficients and position of sample points can be chosen such that the integration is exact Formation of global stiffness matrix Assembling of element stiffness matrices in global matrix Computational Geotechnics Finite Element Method in Geotechnical Engineering

Formulation of Stiffness Matrix K is often symmetric and has a band-form: (# are non-zero’s) Computational Geotechnics Finite Element Method in Geotechnical Engineering

Solution of Equation Global system of equations: KD = R R is force vector and contains loadings as nodal forces Usually in incremental form: Solution: (i = step number)

Solution of Equations From solution of displacement Strains: Stresses: Computational Geotechnics Finite Element Method in Geotechnical Engineering