Finite Elements Fournoded rectangular element Finite element formulation



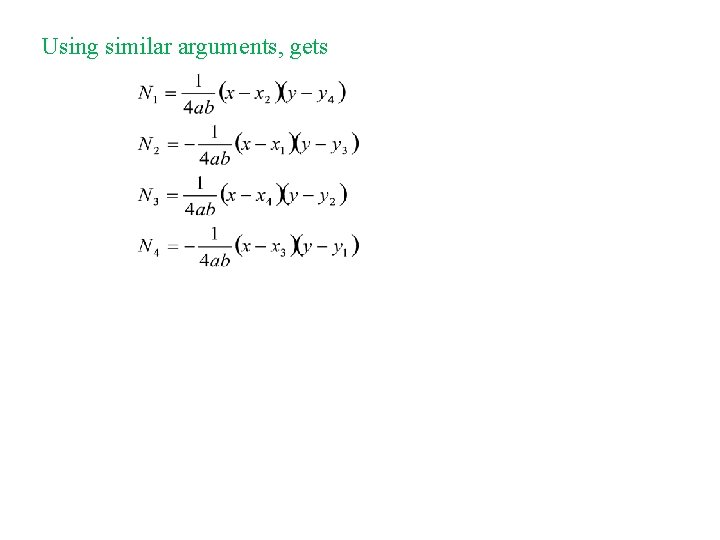








- Slides: 17

Finite Elements Four-noded rectangular element

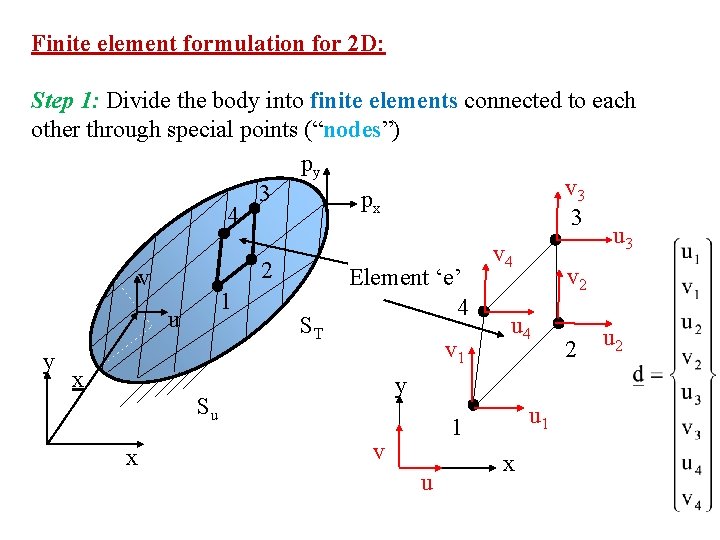
Finite element formulation for 2 D: Step 1: Divide the body into finite elements connected to each other through special points (“nodes”) py v 3 3 px 4 3 u 3 v 4 2 v 2 Element ‘e’ v 1 4 u u 4 ST v 1 2 u 2 y x y Su u 1 1 v x x u

Summary: For each element Displacement approximation in terms of shape functions Strain approximation in terms of strain-displacement matrix Stress approximation Element stiffness matrix Element nodal load vector

4 -noded rectangular element with edges parallel to the coordinate axes: (x 4, y 4) 4 3 (x 3, y 3) v u 2 b (x, y) y 1 (x 1, y 1) 2 a 2 (x 2, y 2) x • 4 nodes per element • 2 dofs per node (each node can move in x- and y- directions) • 8 dofs per element

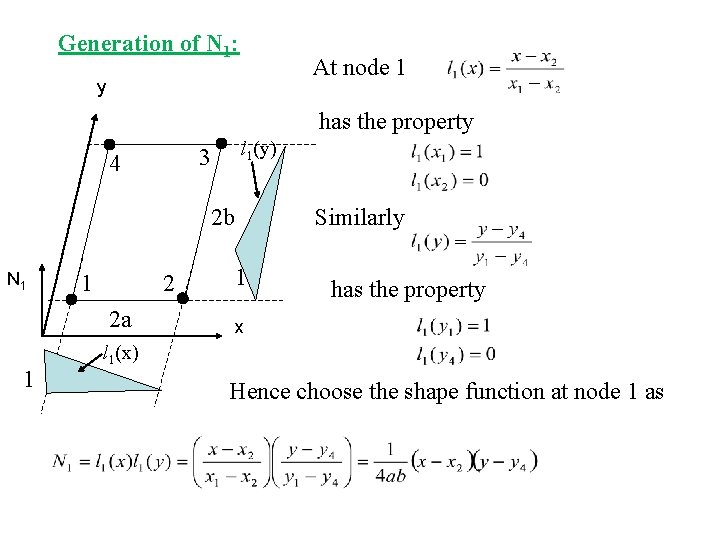
Generation of N 1: At node 1 y has the property l 1(y) 3 4 2 b N 1 1 2 2 a 1 Similarly 1 has the property x l 1(x) Hence choose the shape function at node 1 as
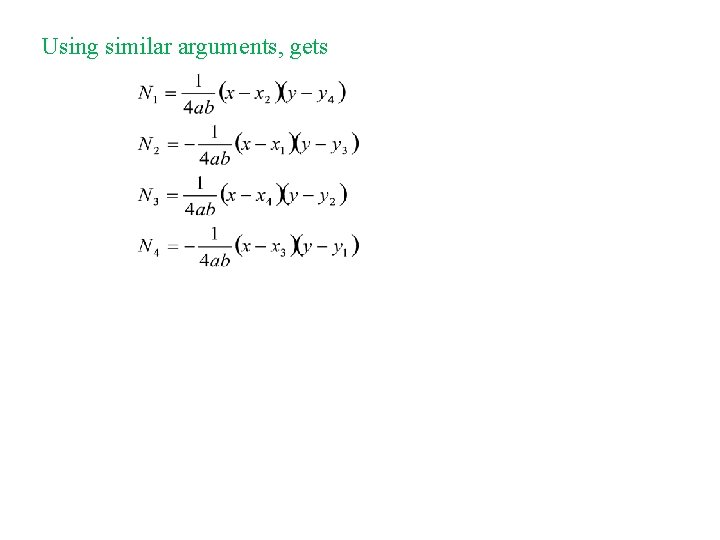
Using similar arguments, gets

Properties of the shape functions: 1. The shape functions N 1, N 2 , N 3 and N 4 are bilinear functions of x and y 2. Kronecker delta property 3. Completeness

4. Along lines parallel to the x- or y-axes, the shape functions are linear. But along any other line they are nonlinear. 5. An element shape function related to a specific nodal point is zero along element boundaries not containing the nodal point. 6. The displacement field is continuous across elements 7. The strains and stresses are not constant within an element nor are they continuous across element boundaries.

The strain-displacement relationship Notice that the strains (and hence the stresses) are NOT constant within an element

Computation of the terms in the stiffness matrix of 2 D elements v 4 4 v 3 u 4 The B-matrix (strain-displacement) corresponding to this element is 3 u 1 v y v 1 (x, y) v 1 u 2 v 2 u 3 v 2 u 2 1 u 2 x We will denote the columns of the B-matrix as v 3 u 4 v 4

The stiffness matrix corresponding to this element is which has the following form u 1 v 1 u 2 v 2 u 3 v 3 u 4 v 4 The individual entries of the stiffness matrix may be computed as follows

Notice that these formulae are quite general (apply to all kinds of finite elements, CST, quadrilateral, etc) since we have not used any specific shape functions for their derivation.

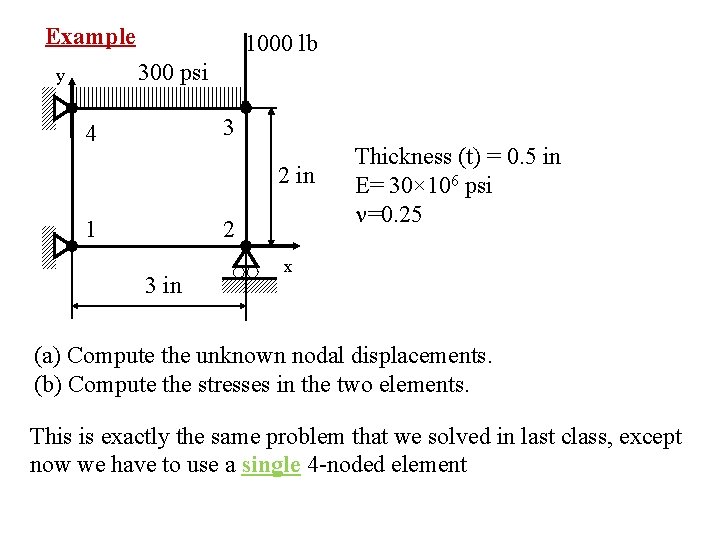
Example 1000 lb 300 psi y 3 4 2 in 1 2 3 in Thickness (t) = 0. 5 in E= 30× 106 psi n=0. 25 x (a) Compute the unknown nodal displacements. (b) Compute the stresses in the two elements. This is exactly the same problem that we solved in last class, except now we have to use a single 4 -noded element

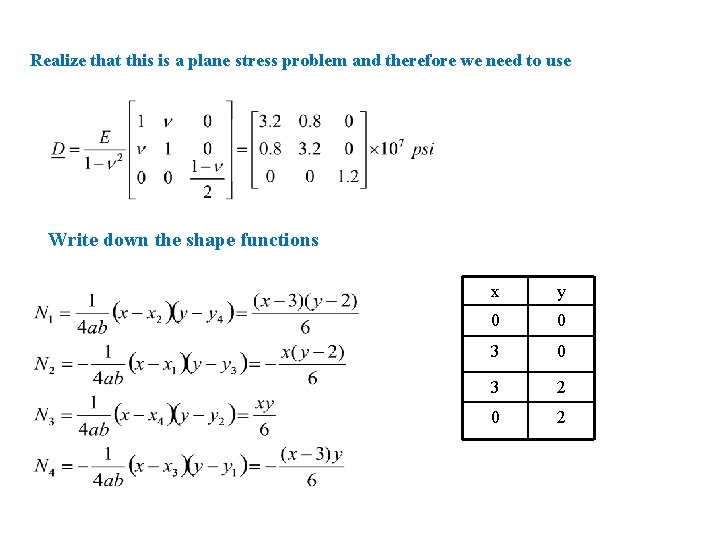
Realize that this is a plane stress problem and therefore we need to use Write down the shape functions x y 0 0 3 2 0 2

We have 4 nodes with 2 dofs per node=8 dofs. However, 5 of these are fixed. The nonzero displacements are u 2 u 3 v 3 Hence we need to solve u 2 u 3 v 3 Need to compute only the relevant terms in the stiffness matrix

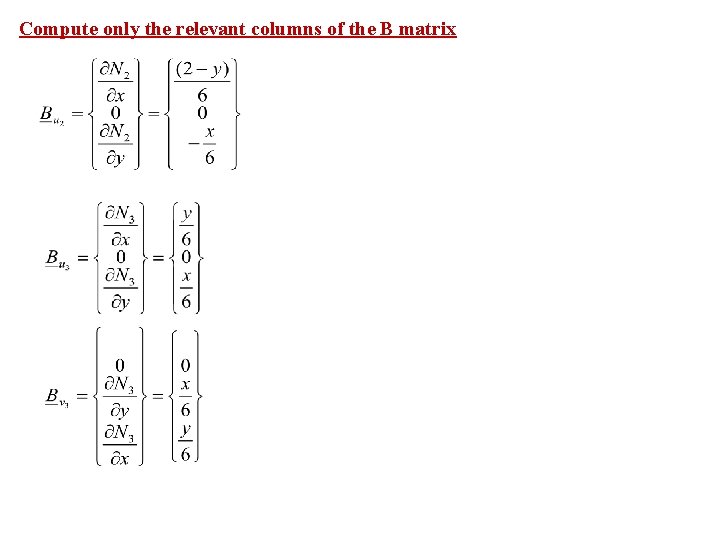
Compute only the relevant columns of the B matrix

Similarly compute the other terms.