Finite Elements in multidimensions Sauro Succi Finite Elements




























- Slides: 39

Finite Elements in multi-dimensions Sauro Succi

Finite Elements: full power! The power of FEM remains somehow silent in d=1, much more visible in d=2 and d=3, where geometrical complexity is often the key factor

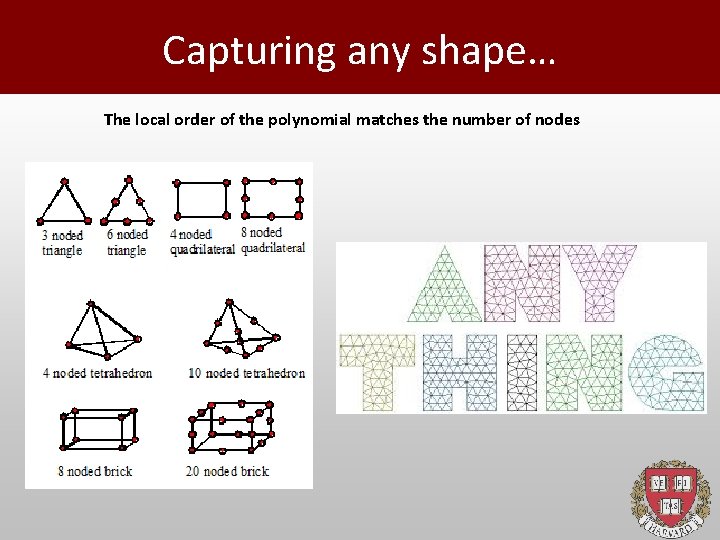
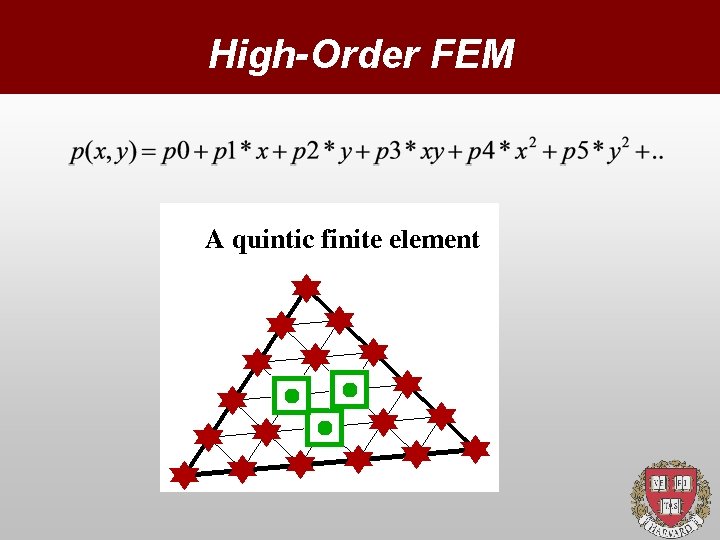
Capturing any shape… The local order of the polynomial matches the number of nodes

High-Order FEM

2 D FEM: structural mechanics Local deformation of a solid body obeys forced wave equation (small amplitudes): FEM “pyramid functions” (2 d hat): Leads to semidiscrete ODE’s:

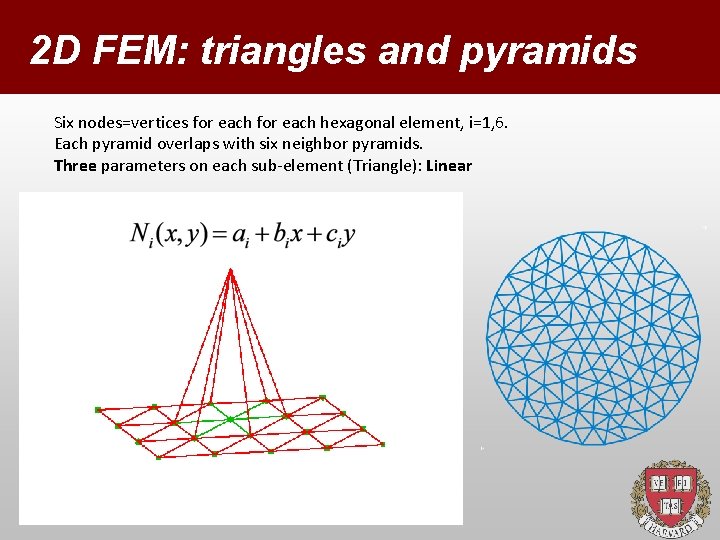
2 D FEM: triangles and pyramids Six nodes=vertices for each hexagonal element, i=1, 6. Each pyramid overlaps with six neighbor pyramids. Three parameters on each sub-element (Triangle): Linear

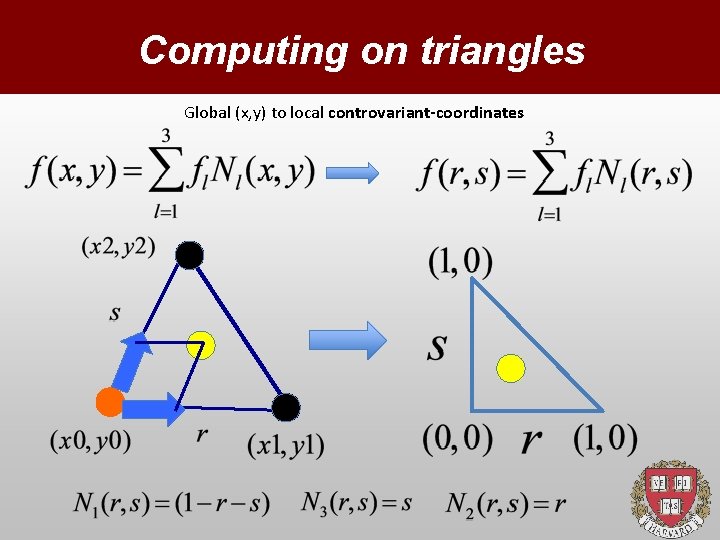
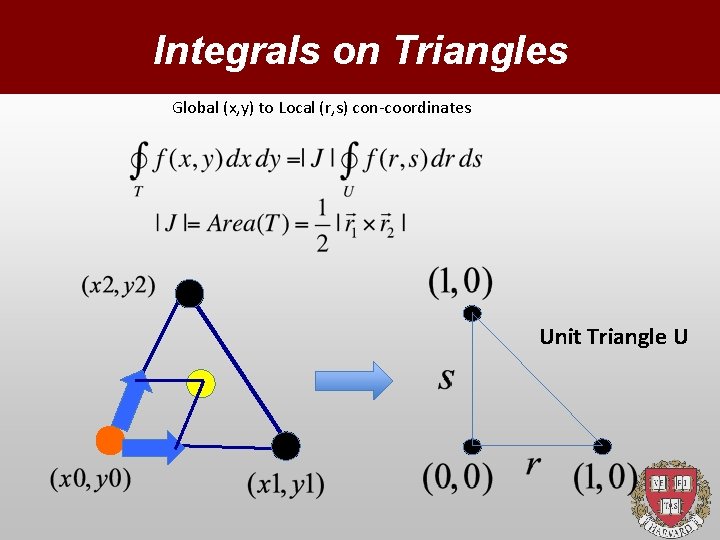
Computing on triangles Global (x, y) to local controvariant-coordinates

Contro-variant coordinates Global (x, y) to Local (r, s) con-coordinates

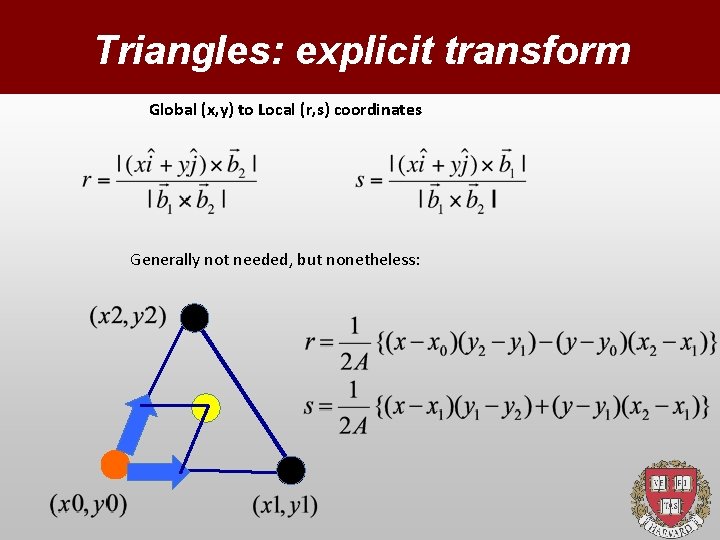
Triangles: explicit transform Global (x, y) to Local (r, s) coordinates Generally not needed, but nonetheless:

Integrals on Triangles Global (x, y) to Local (r, s) con-coordinates Unit Triangle U

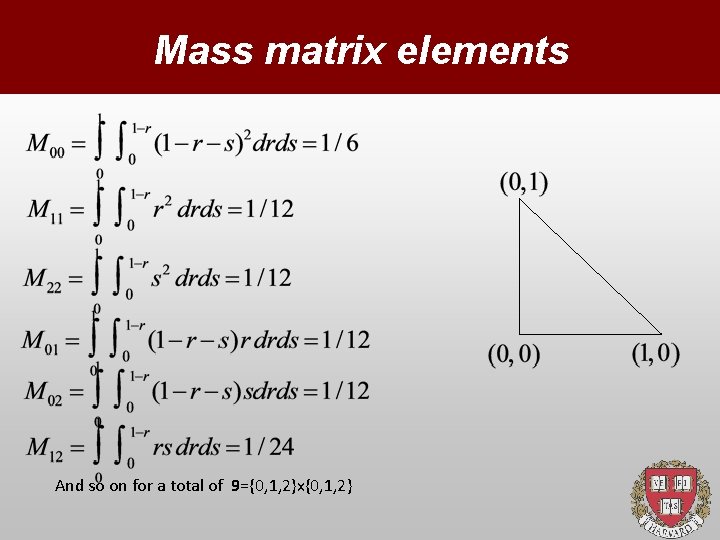
Mass matrix elements And so on for a total of 9={0, 1, 2}x{0, 1, 2}

Matrix elements: quadrature How about generic integrals of the form? Quadrature Formulas on Triangles: Order 1: exact for {1, r, s} Order 2: exact for {1, r, s, r*r, r*s, s*s}

Stiffness matrix elements Each triangle sharing i and j as vertices contributes to the matrix element (i, j): Now the area is not sufficient, local metric factors {a, b, c, d} enter explictly

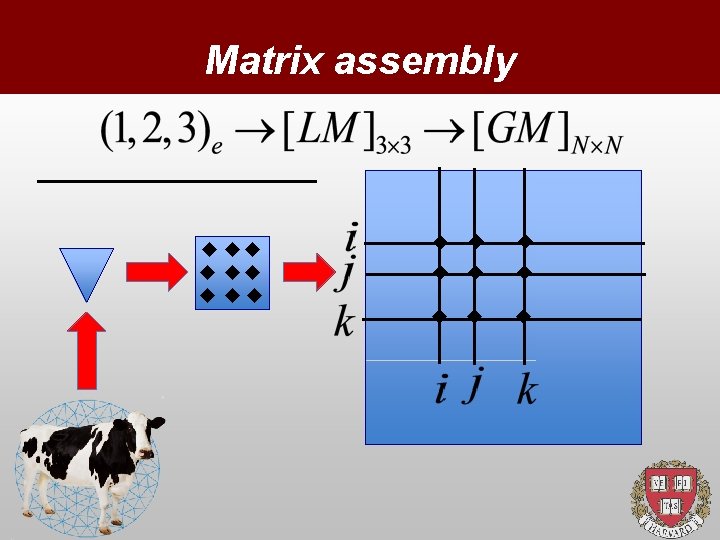
Matrix assembly Each finite-element centered on the node j, connects to Z(j) neighbors. Each sub-element (triangle) contains 3 nodes: {x 1, y 1; x 2, y 2; x 3, y 3} and a pointer to the global address: p(e, 1)=i 1, p(e, 2)=i 2, p(e, 3)=i 3. Sub-elements are the fundamental geometric units! For all e=1, Nel The list of node coordinates, elements, connectivicty and metric factors must be prepared before hand: MESHING. This is the most crucial step (Pre-Processing), since the quality of the mesh is key to a successful simulation!

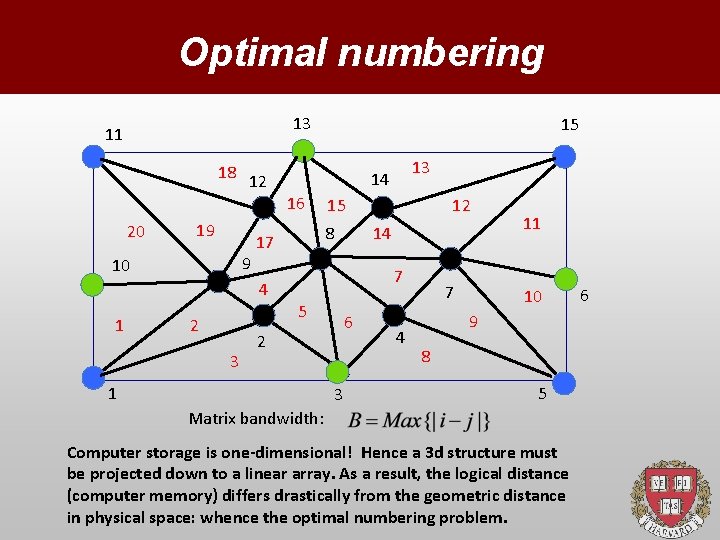
Element-wise assembly Local to Global matrix: The local to global mapping must be designed so as to Minimise the Logical distance {i-j} over the entire mesh. This is key for direct methods, but always beneficial. Optimal numbering is a NP-complete problem! (Travel-sales man-like)

Matrix assembly

Linear Algebra Direct Methods: Minimize bandwidth Optimal Numbering (NP complete) Iterative Methods: Sparse matrix algebra: y=A*x

Optimal numbering 13 11 18 20 12 19 9 10 1 2 3 13 14 16 12 15 8 17 4 15 14 7 5 6 2 1 3 4 7 11 10 9 8 5 Matrix bandwidth: Computer storage is one-dimensional! Hence a 3 d structure must be projected down to a linear array. As a result, the logical distance (computer memory) differs drastically from the geometric distance in physical space: whence the optimal numbering problem. 6

Geo-Topological Data Metric File Nodes 1 2 Node Coordinates x 1, y 1, z 1 x 2, y 2, z 2 … N …. . x. N, y. N, z. N Node Id nid(1)={0, 1, 2} 11 nid(N) Topology File Element 1 2 Three nodes indices i(1), j(1) k(1) i(2), j(2), k(2) … Nel …. . i(Nel) j(Nel), k(Nel) 20 10 9

Sparse FEM matrices This structure refelects the geometrical connectivity (# of non-zero elements per row) and the Numbering policy (Bandwidth)

3 D FEM

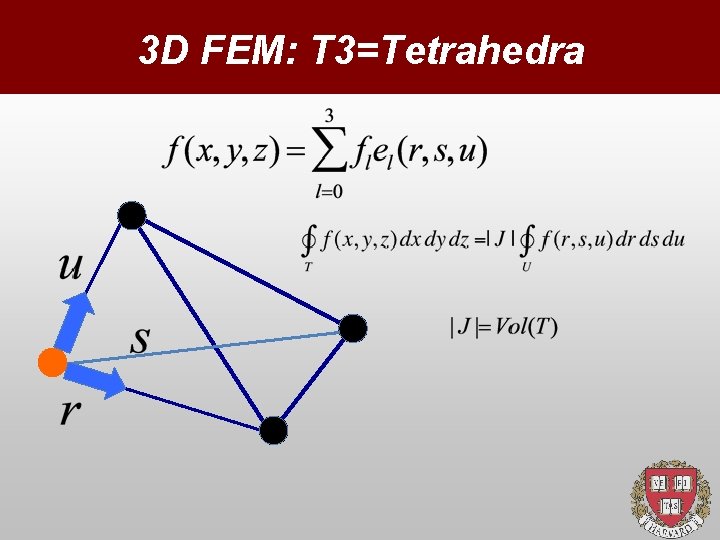
3 D FEM: T 3=Tetrahedra

3 D FEM: Tetrahedra The logical procedure stays the same, but all stages of the calculation are more laborious, in all respects: 4 x 4=16 local matrix elements {i, j, k, l} More metric factors within the T 3=Tetrahedron Larger matrices O(N^3) and bandwidths B=O(N^2) Solid but heavy-duty!

FEM for Navier-Stokes

FEM for NSE: Nonlinearity p is the OUTER iteration, typically the starting point is the value at the previous time-step Not to be confused with the INNER iteration, the one to solve Ax=b by iterative methods (see previous lecture)

FEM operators + Strong math back-up + Very systematic + Fluid/Solid coupling - Expensive (matrix algebra)

Summary FEM + Geometrical flexibility, adaptivity Powerful math backup (weak convergence) Systematic programming. Once the Elements are chosen, all follows automatically no decisions required. FEM Matrix algebra anyway (lumping helps) Heavy duty Bottomline: Mainstream for solid mech, fluid-solid but less for fluids alone.

Open Source and Commercial FEM for Fluids/Solids Open. FOAM (Field Operation and Manipulation) Listed among FEM but it’s FVM? !? COMSOL Multiphysics: (see Wikipedia) Set of flows, Core Numerical methods: Numerical Solver: It is candid about FVM being more popular (simpler) FEM is unsurpassed for structural mechanics (no advection…)

COMSOL




Multi-elements, adapted to The operators (Multiphysics)


Assignements 1. Solve Poisson in a d=2 rectangle using cartesian hat functions (see next slides) 2. Same as 1. using triangles 3. Same as 1 and/or 2. for 2 D Schroedinger

Cartesian 2 d FEM The FEM is composed of 4 sub-elements (triangle). Each sub-element generates 4 x 4=16 local matrix elements. The global matrix contains 9 non-zero elements per row

Cartesian 2 d FEM Since the element is a direct product of x*y 1 d elements, all matrix elements are separable.

Example: 2 d mass matrix Same goes for all other matrices

End of the Lecture
 Sauro succi
Sauro succi Sauro tavarnesi
Sauro tavarnesi Learning objectives of non finite verbs
Learning objectives of non finite verbs Finite and non-finite verb
Finite and non-finite verb Finite subordinate clause
Finite subordinate clause Finite and non finite
Finite and non finite What is finite verb
What is finite verb Finite element method
Finite element method Finite state machine game
Finite state machine game Finite automata
Finite automata Tcp connection management finite state machine
Tcp connection management finite state machine Finite state machine
Finite state machine Soal uts teori bahasa dan automata
Soal uts teori bahasa dan automata Finite difference time domain
Finite difference time domain Finite differences
Finite differences Kleene theorem part 3
Kleene theorem part 3 Deterministic finite automata adalah
Deterministic finite automata adalah Finite divided difference
Finite divided difference An informal picture of finite automata
An informal picture of finite automata Stifness matrix
Stifness matrix Fem applications
Fem applications Queue waiting time
Queue waiting time Differenze finite centrate
Differenze finite centrate Finite differences exponential functions
Finite differences exponential functions Finite subgroup test
Finite subgroup test Passive gerund and infinitive examples
Passive gerund and infinitive examples Contoh kasus finite state automata
Contoh kasus finite state automata Finite and continuous cell lines
Finite and continuous cell lines Finite capacity
Finite capacity Finite element method
Finite element method Vhdl finite state machine
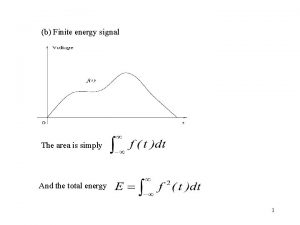
Vhdl finite state machine Energy of signal
Energy of signal Nrm classification
Nrm classification Diagram fsa
Diagram fsa Kevin conroy finite
Kevin conroy finite Finite verb latin
Finite verb latin 10-2 arithmetic sequences and series
10-2 arithmetic sequences and series Finite probability space
Finite probability space Finite risk reinsurance
Finite risk reinsurance Limitations of finite automata
Limitations of finite automata