FD for Nonlinear Conservation Laws Sauro Succi We

FD for Nonlinear Conservation Laws Sauro Succi We discuss NONLINEAR conservative equations: Focus on the Burgers equation for (pressure-free) fluids A beautiful and highly versatile equation in math phys: Shock waves, freak waves, interfacial growth, cosmology…

Non. Lin Conservation equations Hyperbolic Conservation equations: The flux(current) vector can take many forms, but we shall focus on AD: HETEROGENEOUS Advection-Diffusion (Fick’s law) Non-linear transport (self-advecting fluids) These covers a vast class of HETEROGENEOUS phenomena, Including Statistical Physics (Fokker-Planck) and Quantum Mechanics (Schroedinger equation)

Fluids: the Navier-Stokes Eqs Mass conservation Momentum conservation (Newton: inertia+pressure+dissipation) Momentum-Flux tensor: The NSE are Nonlinear Tensor PDE’s: Momentum along z Flowing across surface with normal x 3

The incompressible Navier-Stokes Eqs No volume changes Density = constant = 1 Momentum conservation The incompressibility condition (solenoidal flow): Represents a purely kinematic constraint, which holds at any poiint in space at time”: instantaneous propagation. 4

Nonlinear: Burgers (1 d fluid) One dimension: Very dilute, tenuous media (cold plasmas, astrophysics, cosmology) The Burgers equation (1948): Universe: 1 proton/m^3… Conservative form: 5

Nonlinear: Burgers (1 d fluid) (pressure-free) Nonlinear/Diffusion: Reynolds number Prototypical example of shock-generator, freak waves: Why? In the (singular!) inviscid limit Re to infinity: This is a wave equation with speed c=u(x, t), pure kinematics! The traveling speed is maximum where the amplitude is maximum; If u(x) is hump-shaped, the top behind will overtake the front: BREAKING 6

Nonlinear: Burgers (1 d fluid) (pressure-free) Prototypical example of shock-generator, freak waves: Analytical solution: Non-linear traveling wave Self-advection: Let z=x-ct: One quadrature: 7

Nonlinear: Burgers (1 d fluid) One quadrature: Rearrange: Solve (by setting the integration constant to zero): Larger waves travel faster (Tsunami), (typical nonlinear) 8

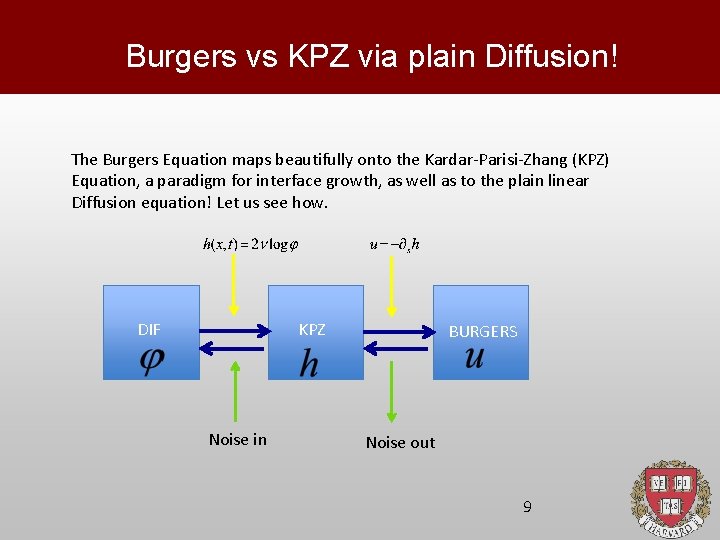
Burgers vs KPZ via plain Diffusion! The Burgers Equation maps beautifully onto the Kardar-Parisi-Zhang (KPZ) Equation, a paradigm for interface growth, as well as to the plain linear Diffusion equation! Let us see how. DIF KPZ Noise in BURGERS Noise out 9

Diffusion to KPZ DIFFUSION KPZ Take the simple DE: Hopf-Cole transformation: Simple algebra yields: Add random source (“rain”): This is the famous KPZ equation for random growth! 10

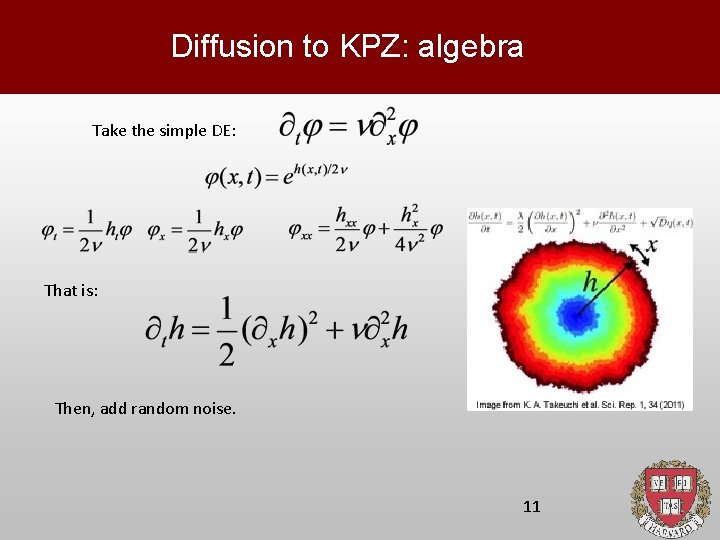
Diffusion to KPZ: algebra Take the simple DE: That is: Then, add random noise. 11

KPZ to Burgers KPZ BURGERS Take noiseless KPZ: Let: (Slope of the interface) Hopf-Cole : Take d/dx : That is: which is Burgers! q. e. d 12

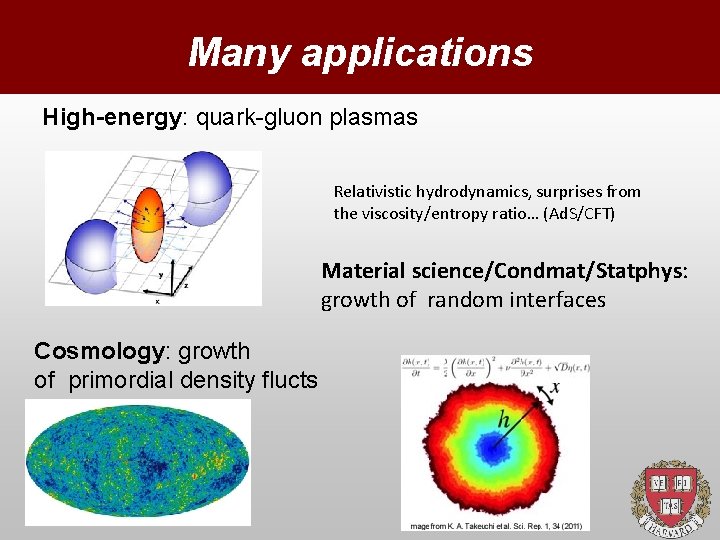
Many applications High-energy: quark-gluon plasmas Relativistic hydrodynamics, surprises from the viscosity/entropy ratio… (Ad. S/CFT) Material science/Condmat/Statphys: growth of random interfaces Cosmology: growth of primordial density flucts 13

Burgers in Cosmology Large-scale structure of the Universe: primordial density perturbations: random fields originated by early quantum fluctuations amplified by hydrodynamic motion. Major obstacle: non-linear growth of highly inhomogeneus fields. Solve Einstein cosmological eqs+Burgers equation: WMAP density flucts 14

Equations of state Ideal non-relativistic gas: Radiation: Pressure Note that in general W is NOT the sound speed squared: Standard fluids: Density They are the same only for linear Eo. S Exotic matter: 15

Cosmological fluids 16

Non-ideal cosmological fluids 17

Burgers+Einstein FRW cosmology: Where: Density fluctuations, grow due to gravitational instability Hubble factor Peculiar speed of the galaxy Gravitational potential 18

Numerics 19

Burgers: discretization Fully explicit (Euler) + centered FD: wdll known by now… In compact matrix form: The CFL is local and nonlinear: Small viscosities are dangerous, as usual. Many variants (besides reducing timestep) 20

Burgers: Lax discretization Interesting variant (P. Lax): Note that: So, Lax adds a gradient dependent numerical viscosity: smoothing effect. All the trickery discussed for the continuity equation (flux-limiters, TVD…) apply here! (see forthcoming P. Mocz lecture) 21

Implicit Time Marching We have seen that the diffusive CFL is way more stringent than the The advective one, so how about: Advection: Explicit (Euler), Diffusion: Implicit In compact matrix form M*u_new=N*u_old=b: This allows larger time-steps, but one must solve a matrix problem M*u=b at each time-step… Not much used if the phenomenon is highly dynamics, very much used 22 In quantum mechanics (see forthcoming lectures)

Burgers: discretization Fully explicit (Euler): CFL still applies but advection is NON-LINEAR: Semi-implicit: CFL is gone, but accuracy must be watched out (For the detail-thirsty, see Burgers. Lecture. pdf) 23

Other beautiful Nonlinear PDE’s 24

Korteweg-De Vries Nonlinear Dispersive waves: Linear Disp. Rel. Conservative form: Short scales travel faster: precursors Nonlinearity and dispersion come to a balance and generate Localized traveling solutions: solitons. Important not only in fluid mechanics, but also particle physics, quantum optics and math phys in general Maps one-to-one to the non-linear Schroedinger equation (Gross-Pitaevski) 25

The superposition of nonlinear Localized waves keeps its coherence in time! (Shallow water fluid dynamcs)) 26

Korteweg-De Vries: Numerics Similar to Burgers, but 3° order spatial derivatives: Exercise: Find A 1 and A 2 such that Error = O(d^2) Answer: 27

What happens to the Dispersion Relation with nonlinear Eqs? 28

Burgers: Dispersion relation By the convolution theorem: The Fourier Transform of the Product is a convolution in k-space: non-local! The relation between omega and k is no longer 1: 1: Non-linear broadening. For each k there is a band of omegas: 29

The KPZ equation (stochastic PDE) 30

Solving the KPZ equation KPZ is a paradigm for interface growth phenomena  It can be viewed as an ADR equation with U=-(Lambda/2) nabla h + linear stochastic noise. Note that the nonlinearity parameter Lambda has dimensions of velocity. The ratio Growth/Diffusion is Lambda*h/nu, so it grows with The growing interface… It is the analogue of the Reynolds number In turbulence (sometimes called Burgulence).

Numerical Solution of Stochastic KPZ Noise is zero mean: Noise is delta-correlated (white noise, zero memory) Fluctuation-Dissipation Theorem: Noise is one-one related to diffusion/dissipation 32

Scaling laws: analytical results Mean interface height, length: Roughness ~ Variance=Width squared Higher order statistical moments: Question: How do the moments evolve in time as a function of L? Does the interface smooth out or gets sharper and sharper?

Scaling laws: analytical results Roughness obeys dynamic scaling law: In d=1: a=1/2, b=1/3, z=a/b, a+z=2 in any d W/L scales like L^{a/2 -1} and goes to zero as L goes to infinity

Numerical Solution of Stochastic KPZ Differential Ito calculus: Uniformly distributed random number Note the sqrt (dt) which stems from diffusion: dx^2/dt=const, Hence dt scales like dx^2. Stringent at small dx. The numerical convergence at large lambda’s is still controversial: Fields medal 2014 awarded for convergence properties!!! 35

The sandpile model (Complexity) Instability: Nonlinearity >> Diffusion: When the slope exceeds a critcial value, an instability develops: avalanches. 36

The sandpile model (Cellular Automaton) Sandpile Rule: Rainfall and Redistribution If the total H is finite at time 0, the process is guaranteed to converge, i. e. terminate to a given attractor in a finite time. However, the dynamics can be incredibly rich, avalanches, “earthquakes”, 1/f noise, universal signatures of Complexity. Paradigm of “catastrophic relaxation”. Key: The continuum limit is far from trivial, if it exists at all This is a typical Rule-Driven lattice Model! 37

Now to the code… 38

Assignements 1. Solve the 1 d Burgers (see burgers. f) 2. Solve Burgers with FRW cosmology 3. Solve KPZ in d=1 and check the scaling laws (see kpz. f) 4. Same in d=2 5. Code and run the sandpile, detect avalanches? 39

End of the lecture 40