Nonlinear Sampling Nonlinear Sampling st Memoryless nonlinear distortion

Nonlinear Sampling

Nonlinear Sampling s(-t) Memoryless nonlinear distortion t=n Saturation in CCD sensors Dynamic range correction Optical devices High power amplifiers 2

Easy or Hard? • Memoryless nonlinear M, but ideal samples: Easy Standard setup • Generalized samples but M=I: Easy Assuming => Oblique projection: • Memoryless nonlinear M, generalized samples: but M(A) usually not a subspace … Hard 3

Perfect Reconstruction Theorem (uniqueness): If and m(t) is invertible and smooth enough then y(t) can be recovered exactly Setting: m(t) is invertible with bounded derivative y(t) is lies in a subspace A Uniqueness same as in linear case! Proof: Based on extended frame perturbation theory and geometrical ideas 4

Optimization Based Approach Main idea: 1. Minimize error in samples 2. From uniqueness if Perfect reconstruction where global minimum of Difficulties: 1. Nonlinear, nonconvex problem 2. Defined over an infinite space Theorem : Under the previous conditions any stationary point of is unique and globally optimal Only have to trap a stationary point! 5

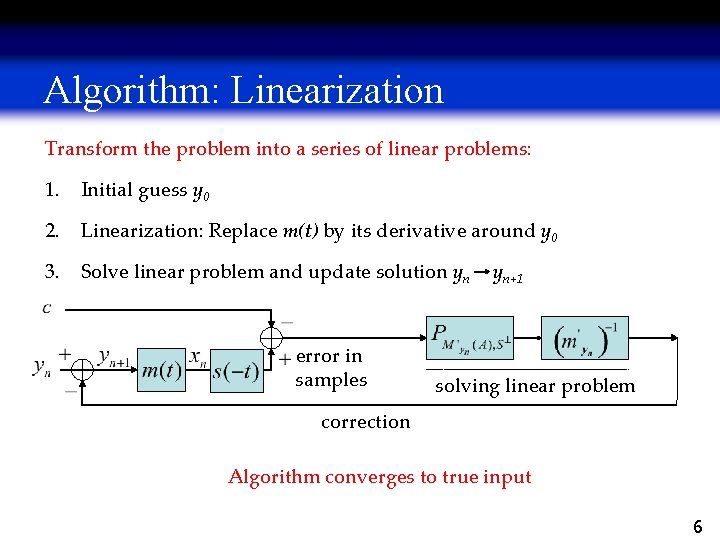
Algorithm: Linearization Transform the problem into a series of linear problems: 1. Initial guess y 0 2. Linearization: Replace m(t) by its derivative around y 0 3. Solve linear problem and update solution yn error in samples yn+1 solving linear problem correction Algorithm converges to true input 6

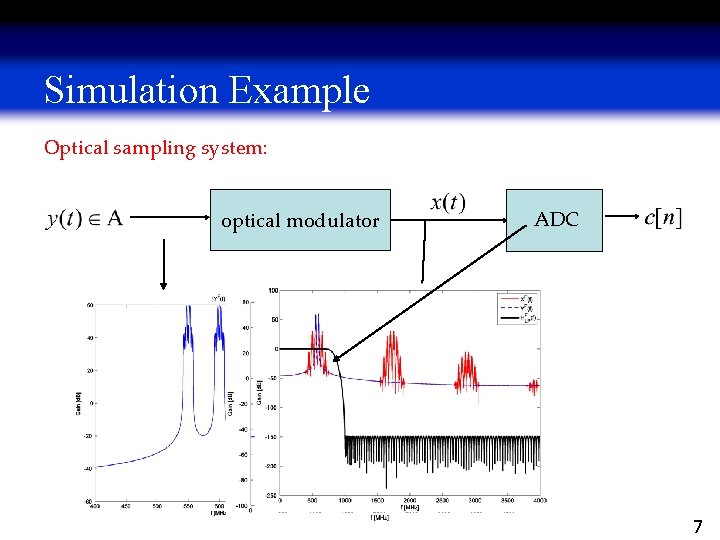
Simulation Example Optical sampling system: optical modulator ADC 7

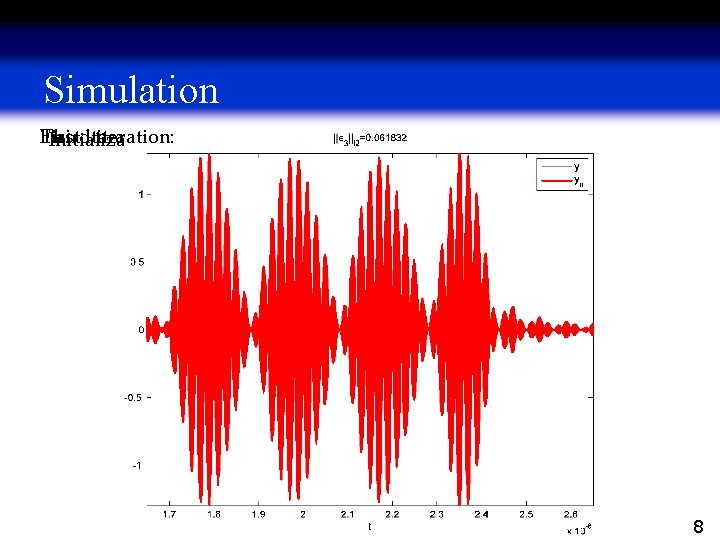
Simulation Third iteration: with First iteration: Initialization 8

Course Summary (So Far …) Crash course on linear algebra Subspace sampling (sampling of nonbandlimited signals, interpolation methods) Minimax recovery techniques Constrained reconstruction: minimax and consistent methods Nonlinear sampling And yet to come … Sampling random signals Sampling sparse signals 9

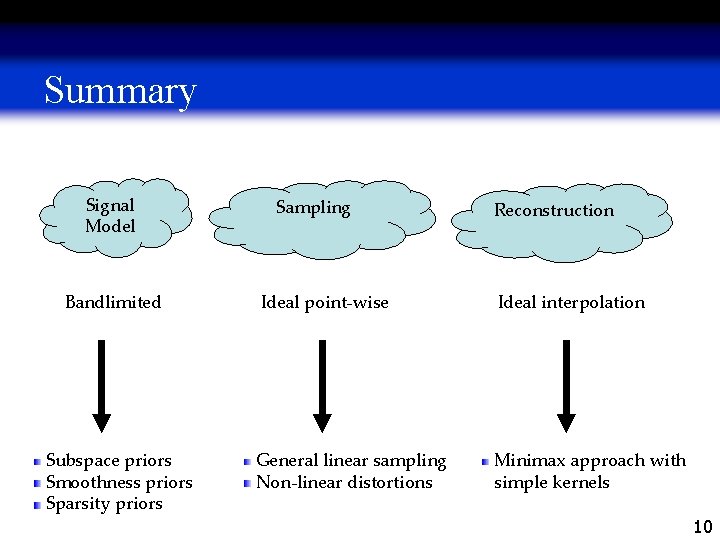
Summary Signal Model Bandlimited Subspace priors Smoothness priors Sparsity priors Sampling Reconstruction Ideal point-wise Ideal interpolation General linear sampling Non-linear distortions Minimax approach with simple kernels 10

Our Point-Of-View Sampling can be viewed in a broader sense of projection onto any subspace Can choose the subspaces to yield interesting new possibilities: Below Nyquist sampling of sparse signals Pointwise samples of non bandlimited signals Perfect compensation of nonlinear effects Perfect recovery of non-bandlimited signals after LPF … 11