Channel Coding Theorem The most famous in IT

Channel Coding Theorem (The most famous in IT) Channel Capacity; Problem: finding the maximum number of distinguishable signals for n uses of a communication channel. This number grows exponentially with n, and the exponent is known as the channel capacity.

Mathematical model The mathematical analog of a physical signaling system is shown. Problem: two different input sequences may give rise to the same output sequence; the inputs are confusable. We show that we can choose a “nonconfusable” subset of input sequences so that with high probability there is only one highly likely input that could have caused the particular output.

Definitions Definition discrete channel : ( , p(y|x), Y) a system consisting of an input alphabet and output alphabet Y (finite and a probability transition matrix p(y|x) that expresses the probability o observing the output symbol y given that we send the symbol x. The channel is said to be memoryless if the probability distribution of the depends only on the input at that time and is conditionally independent o previous channel inputs or outputs. Definition “information” channel capacity of a discrete memor

Examples Of Channel Capacity Noiseless Binary Channel Any transmitted bit is received without error One error-free bit can be transmitted per use of the channel, so the capacity is 1 bit. Or, by the definition of C : C = max I (X; Y) =1 bit, achieved by: p(x) = (1/2, 1/2).

Examples Of Channel Capacity Noisy channel with nonoverlapping outputs The input can be determined from the output C = max I (X; Y) = 1 bit, achieved by : p(x) = (1/2, 1/2).

Examples Of Channel Capacity Noisy Typewriter the channel input is either received unchanged at the output with probability 1/2 or is transformed into the next letter with probability 1/2 C = max I (X; Y) = max (H(Y ) − H(Y|X)) = max. H(Y) − 1 = log 26 − 1 = log 13, achieved by using p(x) distributed uniformly over all the inputs.

Examples Of Channel Capacity Binary Symmetric Channel This is a model of a channel with errors, all the bits received are unreliable. Equality is achieved when the input distribution is uniform. Hence, the information capacity of a binary symmetric channel with parameter p is C = 1 − H(p) bits.

Examples Of Channel Capacity Binary Erasure Channel A fraction α of the bits are erased. The receiver knows which bits have been erased. [Han Vinck; Essen: ] P(X=0) = P 0 I(X; Y) = H(X) – H(X|Y) H(X) = H(P 0 ) H(X|Y) = α H(X) = α H(P 0) Thus, Cerasure = 1 – α

Properties Of Channel Capacity 1. C ≥ 0 since I (X; Y) ≥ 0. 2. C ≤ log | | since C = max I (X; Y) ≤ max. H(X) = log | |. 3. C ≤ log | Y | for the same reason. 4. I (X; Y) is a continuous function of p(x). 5. I (X; Y) is a concave function of p(x) (Theorem 2. 7. 4). So a local maximum is a global maximum. From properties 2 and 3, the maximum is finite, and we are justified in using the term maximum.

PREVIEW OF THEOREM (AEP again!) For large block lengths, every channel looks like th noisy typewriter channel and the channel has a su of inputs that produce essentially disjoint sequence the output. For each (typical) input n-sequence, there approximately 2 n. H(Y |X) possible Y sequences, all of them equally likely. We wish to ensure that n two X sequences produce the same Y output sequ Otherwise, we will not be able to decide which X sequence was sent. The total number of possible (typical) Y sequences ≈ 2 n. H(Y ). This set has to be divided into sets of size 2 n. H(Y |X) corresponding to the different input X sequences. The total number of disjoint sets is less than or equal to 2 n(H(Y )−H(Y|X)) = 2 n. I (X; Y). Hence, we can send at most ≈ 2 n. I (X; Y) distinguishab sequences of length n.

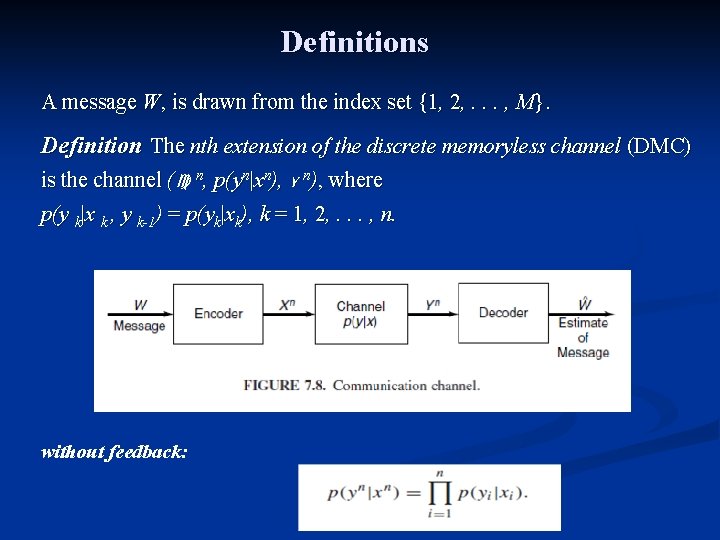
Definitions A message W, is drawn from the index set {1, 2, . . . , M}. Definition The nth extension of the discrete memoryless channel (DMC) is the channel ( n, p(yn|xn), Y n), where p(y k|x k , y k-1) = p(yk|xk), k = 1, 2, . . . , n. without feedback:

Definitions Definition An (M, n) code for the channel ( , p(y|x), Y) consists of the following: 1. An index set {1, 2, . . . , M}. 2. An encoding function Xn : {1, 2, . . . , M} → n, yielding codewords xn(1), xn(2), . . . , xn(M). The set of codewords is called the codebook. 3. A decoding function g : Y n → {1, 2, . . . , M}. Definition (Conditional probability of error) Let be the conditional probability of error given that index i was sent.

Definitions Definition The maximal probability of error λ(n) for an (M, n) code is defined as Definition The (arithmetic) average probability of error Pe(n) for an (M, n) code is defined as

Definitions Definition The rate R of an (M, n) code is Definition A rate R is said to be achievable if there exists a sequence of (2 n. R , n) codes such that the maximal probability of error λ(n) tends to 0 as n→∞. We write (M= 2 n. R, n) codes to mean (2 n. R , n) codes. This will simplify the notation. Definition The (operational) capacity of a channel is the supremum of all achievable rates. Thus, rates less than capacity yield arbitrarily small probability of error for sufficiently large block lengths.

Jointly Typical Sequences Definition The set Aε(n) of jointly typical sequences {(xn, yn)} with respect to the distribution p(x, y) is the set of nsequences with empirical entropies ε-close to the true entropies: Where:

Jointly Typical Sequences

Jointly Typical Sequences There about 2 n. H(X) typical X sequences and about 2 n. H(Y ) typica sequences. However, since there are only 2 n. H(X, Y ) jointly typical se not all pairs of typical Xn and typical Yn are also jointly typical. The probability that any randomly chosen pair is jointly typical is ab 2−n. I (X; Y). Hence, we can consider about 2 n. I (X; Y) such pairs before w likely to come across a jointly typical pair. This suggests that there about 2 n. I (X; Y) distinguishable signals Xn. Proof #3:

Channel Coding Theorem (7. 7. 1) (Channel coding theorem) For a discrete memoryless channel, all rates below capac achievable. Specifically, for every rate R < C, there exists of (2 n. R, n) codes with maximum probability of error λ(n) → Conversely, any sequence of (2 n. R, n) codes with λ(n) → 0 R ≤ C. Proof, Achievability Consider the following:

Proof, Achievability 1. A random code C is generated according to p(x). 2. The code C is then revealed to both sender and receiver. Both sender and receiver are also assumed to know the c transition matrix p(y|x) for the channel. 3. A message W is chosen according to a uniform distribution 4. The w th codeword Xn(w), is sent over the channel. 5. The receiver receives a sequence Yn according to the distribution 6. The receiver guesses which message was sent.

Proof, Achievability The receiver declares that the index Ŵ was sent if the following conditions are satisfied: Let E be the event {Ŵ ≠ W}. By the symmetry of the code construction, the average probability of error averaged over all codes does not dep on the particular index that was sent. Thus, we can assume without loss of generality th the message W = 1 was sent.

Proof, Achievability Define the following events: Where Ei is the event that the ith codeword and Yn are jointly typical. Recall that Yn is the result of sending the first codeword Xn(1) over the channel. Then an error occurs in the decoding scheme if either E 1 occurs, or E 2 ∪ E 3 ∪ · · · E 2 ∪ n. R occurs. Hence, letting P(E) denote Pr(E|W = 1) (note: these are equal):

Proof, Achievability Now, by the joint AEP, The probability that Xn(i) and Yn are jointly typical is 2 -n(I(x; y)-3ε) , (i ≠ 1), Thus:

Proof, Achievability If n is sufficiently large and R < I(X; Y) − 3ε. Hence, if R < I(X; Y), we can choose ε and n so that the average probability of error, averaged over codebooks and codewords, is less than 2ε. To finish the proof, we need a series of reasoning and code selec

Proof, The Converse Lemma 7. 9. 2 Let Yn be the result of passing Xn through a disc channel of capacity C. Then Proof :

Zero-error Codes To obtain a strong bound, we arbitrarily assume that W is uniform distributed over {1, 2, . . . , 2 n. R}. Thus, H(W) = n. R. We can now wr Hence, for any zero-error (2 n. R, n) code, for all n, R ≤ C.

Proof, The Converse We have to show that any sequence of (2 n. R, n) codes with λ(n) → 0 have R ≤ C. If the maximal probability of error tends to zero, the av probability Pe(n) of error goes to zero, Dividing by n, we obtain:

Proof, The Converse Now letting n→∞, we should have R ≤ C. We can rewrite this as: if R > C, the probability of error is bounded away from 0 for sufficiently large n.