Channel Coding www assignmentpoint com Channel Coding is

Channel Coding www. assignmentpoint. com

Channel Coding is kind of signal transformation to improve performance of communication systems. Encoded signal can resist the impacts of noise interference and fading of channel hence improving error detection and correction at receiving end with same SNR. The channel encoder adds some redundant bits with original message bits according to the same prescribed value. The channel decoder at receiving end exploits the redundancy to determine the original message bits from coded data of high rate. In this chapter following three Channel Coding techniques will be discussed along with their decoding. üBlock code (linear) üCyclic Redundancy Code (CRC) üConvolutional Code www. assignmentpoint. com üR-S code

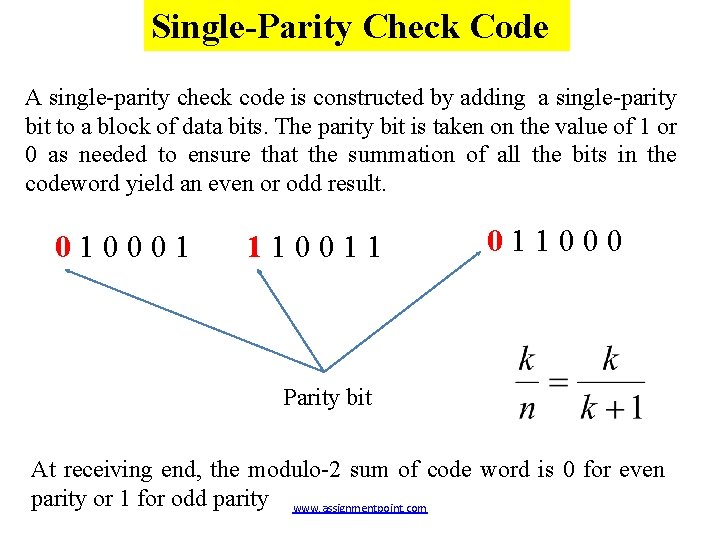
Single-Parity Check Code A single-parity check code is constructed by adding a single-parity bit to a block of data bits. The parity bit is taken on the value of 1 or 0 as needed to ensure that the summation of all the bits in the codeword yield an even or odd result. 010001 110011 011000 Parity bit At receiving end, the modulo-2 sum of code word is 0 for even parity or 1 for odd parity www. assignmentpoint. com

If the number of erroneous bits are even the receiver can not detect the error called undetected error. This coding can detect error but can not correct it. Let all bit errors are equally likely and occurs independently. We can write the probability of j errors occurring in a block of n symbols as, Where p is the probability that a symbol is received in error. The probability of undetected error, www. assignmentpoint. com

Example-1: (4, 3) even-parity error detection. Message 000 001 010 011 100 101 110 111 Parity 0 1 1 0 0 1 Code word 0000 1001 1010 0011 1100 0101 0110 1111 Here n = 4 and k = 3. Now n/2 = 2. Let p = 10 -3 = 6× 10 -6 www. assignmentpoint. com

Convolutional code In telecommunication, a convolutional code is a type of errorcorrecting code in which each m-bit information symbol (each m-bitstring) to be encoded is transformed into an n-bit symbol, where m/n is the code rate (n ≥ m). www. assignmentpoint. com

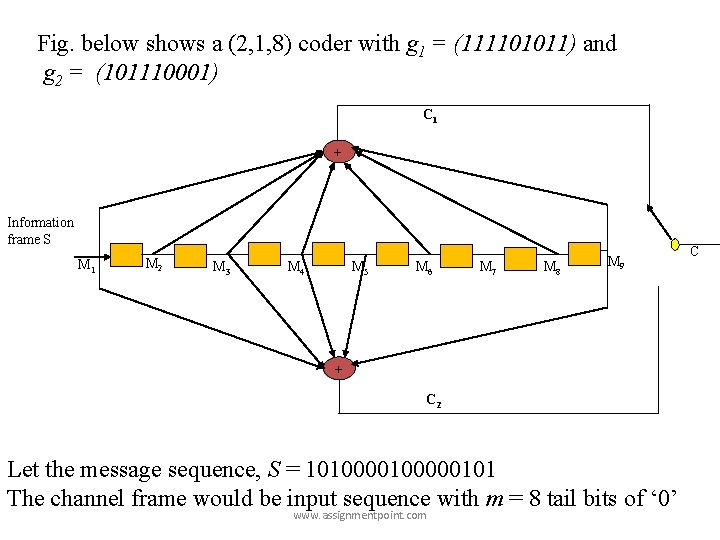
Fig. below shows a (2, 1, 8) coder with g 1 = (111101011) and g 2 = (101110001) C 1 + Information frame S M 1 M 2 M 3 M 4 M 5 M 6 M 7 M 8 M 9 + C 2 Let the message sequence, S = 10100000101 The channel frame would be input sequence with m = 8 tail bits of ‘ 0’ www. assignmentpoint. com C

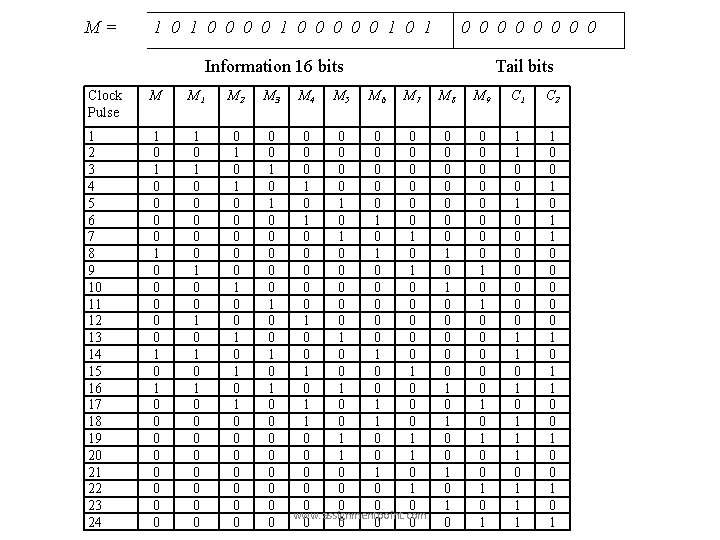
M= 1 0 0 0 0 1 0 0 0 0 Information 16 bits Clock Pulse M M 1 M 2 M 3 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 1 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 1 0 1 0 0 0 0 0 1 0 1 0 0 0 0 M 4 M 5 Tail bits M 6 M 7 0 0 0 1 0 0 1 0 1 0 0 0 0 1 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0 www. assignmentpoint. com 0 0 M 8 M 9 C 1 C 2 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 1 1 1 0 0 0 0 0 1 1 1 0 1 1 0 0 0 1 1 0 0 1 0 1

C = 11 10 00 01 10 01 01 00 00 00 11 10 01 11 00 10 11 10 00 11 10 11 Length of C is 48 bits Length of code sequence is determined using the relation, r = n(S+M) = 2(16+8) = 48 ; where n is the number of output; M is the number of shift register and S is the length of message string. www. assignmentpoint. com

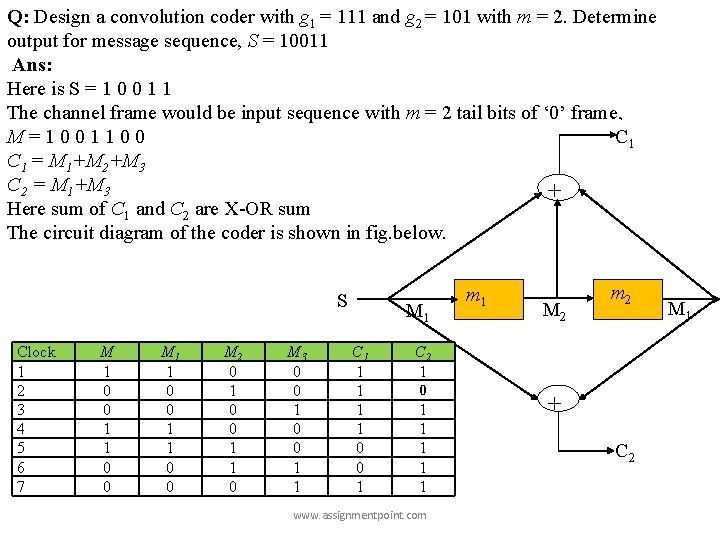
Q: Design a convolution coder with g 1 = 111 and g 2 = 101 with m = 2. Determine output for message sequence, S = 10011 Ans: Here is S = 1 0 0 1 1 The channel frame would be input sequence with m = 2 tail bits of ‘ 0’ frame, M=1001100 C 1 = M 1+M 2+M 3 C 2 = M 1+M 3 + Here sum of C 1 and C 2 are X-OR sum The circuit diagram of the coder is shown in fig. below. S Clock 1 2 3 4 5 6 7 M 1 0 0 1 1 0 0 M 2 0 1 0 0 1 1 0 M 3 0 0 1 1 M 1 C 1 1 1 0 0 1 C 2 1 0 1 1 1 www. assignmentpoint. com m 1 M 2 m 2 + C 2 M 1

C = 11 10 11 11 01 01 11 i. e. the length of codeword is 14 bits. Length of code sequence r = n (S+M) = 2(5+2) = 14 www. assignmentpoint. com

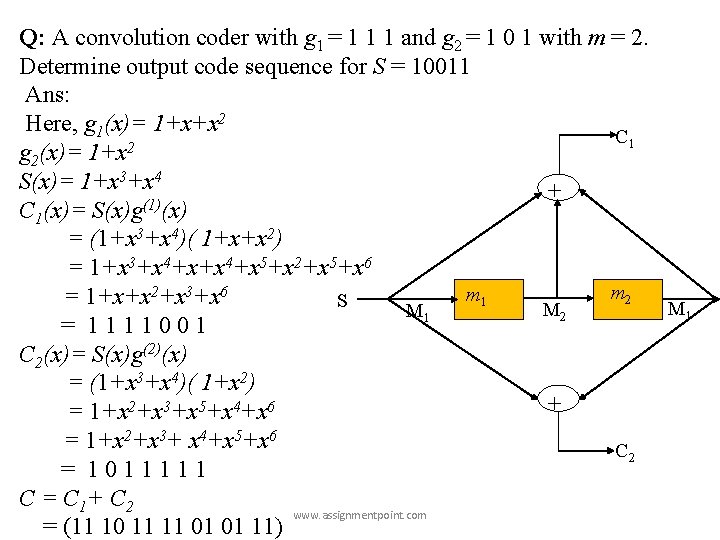
Q: A convolution coder with g 1 = 1 1 1 and g 2 = 1 0 1 with m = 2. Determine output code sequence for S = 10011 Ans: Here, g 1(x)= 1+x+x 2 C 1 2 g 2(x)= 1+x S(x)= 1+x 3+x 4 + (1) C 1(x)= S(x)g (x) = (1+x 3+x 4)( 1+x+x 2) = 1+x 3+x 4+x 5+x 2+x 5+x 6 m 2 m 1 = 1+x+x 2+x 3+x 6 S M 1 M 2 M 1 = 1111001 C 2(x)= S(x)g(2)(x) = (1+x 3+x 4)( 1+x 2) + = 1+x 2+x 3+x 5+x 4+x 6 = 1+x 2+x 3+ x 4+x 5+x 6 C 2 = 1011111 C = C 1+ C 2 www. assignmentpoint. com = (11 10 11 11 01 01 11)

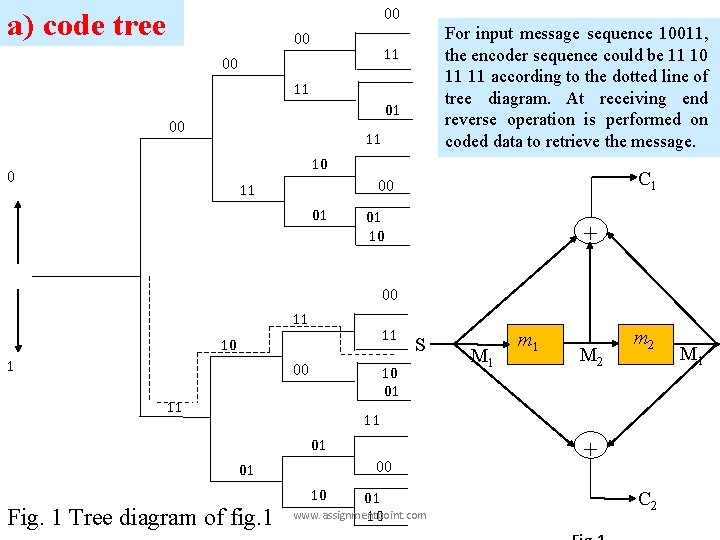
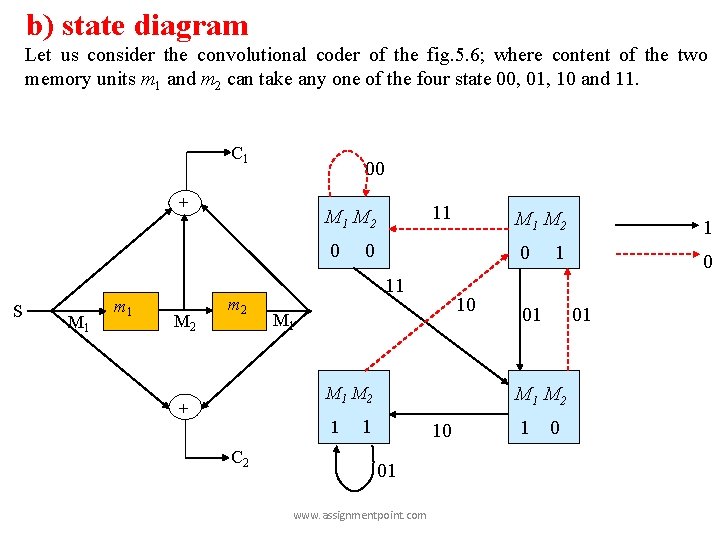
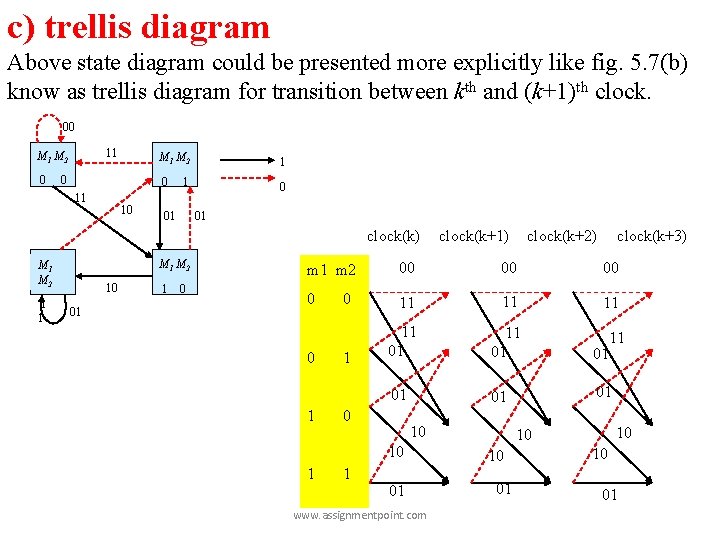
Graphical Presentation of Convoluational Coder A convolutional coder can be expressed in three graphical form a) code tree b) state diagram c) trellis diagram www. assignmentpoint. com

00 a) code tree 00 For input message sequence 10011, the encoder sequence could be 11 10 11 11 according to the dotted line of tree diagram. At receiving end reverse operation is performed on coded data to retrieve the message. 11 00 11 01 00 11 10 0 C 1 00 11 01 01 10 + 00 11 11 10 1 00 S 10 01 11 M 1 m 1 M 2 m 2 11 01 00 01 Fig. 1 Tree diagram of fig. 1 10 01 www. assignmentpoint. com 10 + C 2 M 1

b) state diagram Let us consider the convolutional coder of the fig. 5. 6; where content of the two memory units m 1 and m 2 can take any one of the four state 00, 01, 10 and 11. C 1 00 + 0 S M 1 m 1 M 2 11 M 2 m 2 0 11 10 M 1 1 C 2 1 0 0 1 01 01 M 2 M 1 M 2 + M 1 M 2 1 10 01 www. assignmentpoint. com 1 0

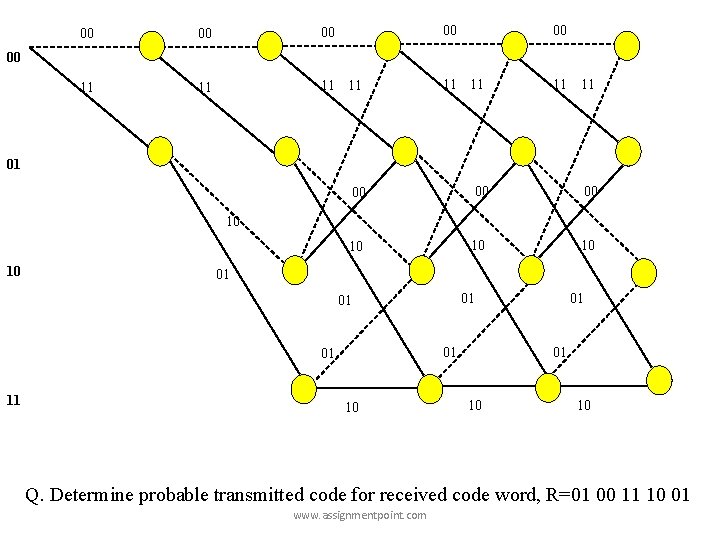
c) trellis diagram Above state diagram could be presented more explicitly like fig. 5. 7(b) know as trellis diagram for transition between kth and (k+1)th clock. 00 11 M 2 0 0 11 10 M 1 M 2 1 0 0 1 01 01 clock(k) M 1 M 2 1 1 10 01 1 0 clock(k+1) clock(k+2) clock(k+3) m 1 m 2 00 00 00 0 0 11 11 11 01 01 0 1 0 10 10 1 1 01 www. assignmentpoint. com 10 10 10 01 11 10 01

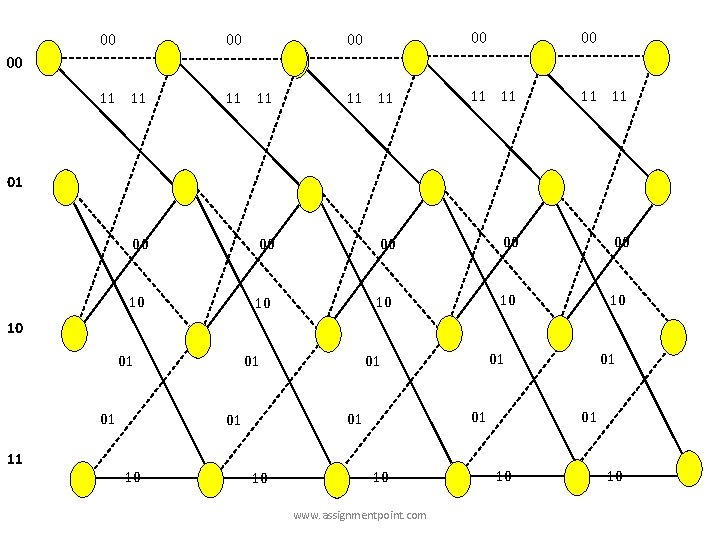
Let us consider a trellis between k and (k+1)th clock shown in fig. 5. 8 00 00 11 11 0 01 1 00 10 11 M 2 01 0 0 11 01 11 10 www. assignmentpoint. com 1 0 0 1 01 01 M 2 M 1 M 2 1 1 10 M 1 M 2 10 01 1 0

00 00 00 11 11 11 00 00 00 10 10 10 00 01 10 01 01 11 10 01 01 01 10 www. assignmentpoint. com 01 01 10 10

00 00 00 11 11 00 11 01 00 00 00 10 10 10 01 01 01 11 10 01 01 10 10 Q. Determine probable transmitted code for received code word, R=01 00 11 10 01 www. assignmentpoint. com

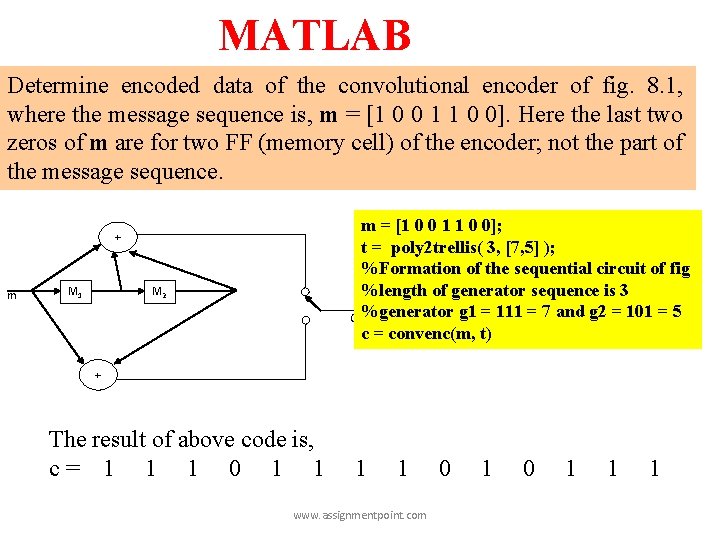
MATLAB Determine encoded data of the convolutional encoder of fig. 8. 1, where the message sequence is, m = [1 0 0 1 1 0 0]. Here the last two zeros of m are for two FF (memory cell) of the encoder; not the part of the message sequence. m = [1 0 0 1 1 0 0]; t = poly 2 trellis( 3, [7, 5] ); %Formation of the sequential circuit of fig %length of generator sequence is 3 C %generator g 1 = 111 = 7 and g 2 = 101 = 5 c = convenc(m, t) + m M 1 M 2 + The result of above code is, c= 1 1 1 0 1 1 www. assignmentpoint. com 0 1 1 1

Let us decode c by Viterbi algorithm. tb=1% traceback depth v=vitdec(c, t, tb, 'cont', 'hard') Above code gives one bit delayed version of message vector, m. v= 0 1 0 0 1 1 0 Determine bit error of above encoder and decoder system. [b, r]=biterr(v(tb+1: end), m(1: end-tb)) b= 0 r= 0 www. assignmentpoint. com

Linear Block Code The linear block code is one type of parity check code expressed by notation (n, k); where k is the length of message bit stream, n is the length of the code word and length of parity bits is n-k. Structure of the (n, k) code word is, b(0) b(1) b(2)…………b(n-k-1) │ m(0) m(1)……m(k-1) n-k k www. assignmentpoint. com

Let us express message block, parity bits and code word in row matrix form. Message, m = [ m(0) m(1) m(2)………m(k-1) ] Parity bits, b = [ b(0) b(1) b(2)………. b(n-k-1) ] Code word, c = [ b(0) b(1)………b(n-k-1) | m(0) m(1) m(2)………m(k-1)] = [ c(0) c(1) c(2)………c(n-1) ] Here parity matrix b is determined using frame encoding rule. b = m. P = [ m(0) m(1)……… m(k-1) ] www. assignmentpoint. com

Here P is a k×n-k matrix of 1 or 0, known as co-efficient matrix. Each row of P is chosen such that they are different from one another. b= = Now code word, C = [ m(0) m(1)…………m(k-1)] = m [ P │ Ik ] ; where, Ik is a k×k identity matrix = m. G ; where, G is known as generator matrix www. assignmentpoint. com

Let us introduce another matrix H of (n-k)×k known as parity check matrix, H = [ In-k │ PT] Now, H G T= [ In-k │ PT] = In-k PT + PTIk = PT+PT =0 Similarly, G HT = 0 At receiving end we receive, c. HT=m. GHT; c=m. G =m× 0 =0 www. assignmentpoint. com

Example - 1 Design a (7, 4 ) linear block code. www. assignmentpoint. com

Error Syndrome Vector: Let the code vector c is transmitted through a noisy channel and at receiving end another vector r is received with the relation, r = c+e ; where e is error vector. Any ith element of e is 1 when an error has occurred at ith position. For no error case all elements of e will be zero. Let us introduce a vector called error syndrome vector, S =r HT = (c + e )H T = c H T+ e H T =0+e HT =e. HT = 1 × n-k matrix For single bit error S= e H T gives ith column of H given error has occurred at ith position. www. assignmentpoint. com

Example-3 Determine error syndrome vector of example-2 for r = [ 0 1 1 0 0 ] and comment on the result. Here, c = [ 0 1 1 0 0 ] and r = [ 0 1 1 0 0 ] e=[0 0 0 1 0 0 0] S = e. H T = [0 0 0 1 0 0 0] = 1 1 0 This is the fourth column of the H matrix, error has occurs at 4 th position of c. www. assignmentpoint. com

Q. (6, 3) linear block code. Let m = [1 1 0] C = m. G = [1 0 1 1 1 0] If r = [0 0 1 1 1 0] The syndrome, S = r. HT = [1 0 0] Therefore error on 1 st bit. www. assignmentpoint. com

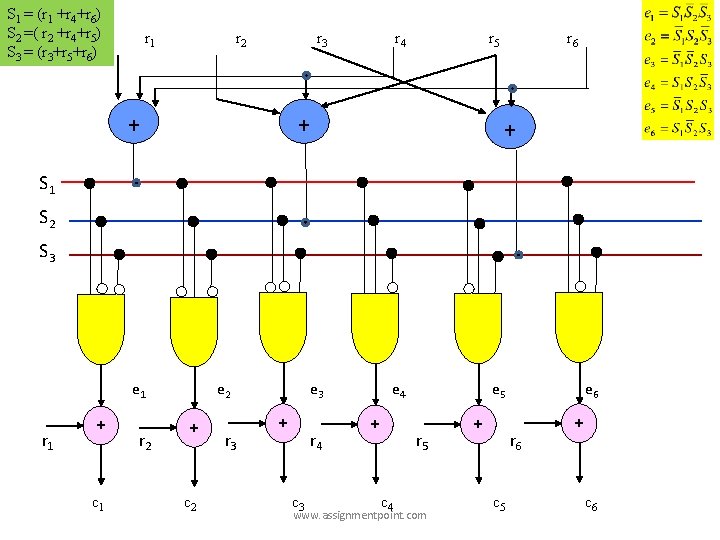
S = r. HT =[r 1 r 2 r 3 r 4 r 5 r 6] = [(r 1 +r 4+r 6) (r 2 +r 4+r 5) S 1= (r 1 +r 4+r 6) S 2= (r 2 +r 4+r 5) S 3= (r 3+r 5+r 6) www. assignmentpoint. com (r 3+r 5+r 6)]

Again , S = r. HT = (c+e)HT= e. HT =[e 1 e 2 e 3 e 4 e 5 e 6] = [ S 1 S 2 S 3] If e = [1 0 0 0 ] then S = e. HT = [1 0 0] i. e 1 st row of HT If e = [0 1 0 0 ] then S = e. HT = [0 1 0] i. e 2 nd row of HT If e = [0 0 1 0 0 0 ] then S = e. HT = [0 0 1] i. e 3 rd row of HT If e = [0 0 0 1 0 0 ] then S = e. HT = [1 1 0] i. e 4 th t row of HT If e = [0 0 1 0 ] then S = e. HT = [0 1 1] i. e 5 th row of HT If e = [0 0 0 1 ] then S = e. HT = [1 0 1] i. e 6 th row of HT www. assignmentpoint. com

If e = [1 0 0 0 ] then S = e. HT = [1 0 0] i. e 1 st row of HT If e = [0 1 0 0 ] then S = e. HT = [0 1 0] i. e 2 nd row of HT If e = [0 0 1 0 0 0 ] then S = e. HT = [0 0 1] i. e 3 rd row of HT If e = [0 0 0 1 0 0 ] then S = e. HT = [1 1 0] i. e 4 th t row of HT If e = [0 0 1 0 ] then S = e. HT = [0 1 1] i. e 5 th row of HT If e = [0 0 0 1 ] then S = e. HT = [1 0 1] i. e 6 th row of HT e 1 1 0 0 0 e 2 0 1 0 0 e 3 0 0 1 0 0 0 e 4 0 0 0 1 0 0 e 5 0 0 1 0 e 6 0 0 0 1 S 1 1 0 0 1 S 2 0 1 1 0 www. assignmentpoint. com S 3 0 0 1 1 Y e 1 e 2 e 3 e 4 e 5 e 6

S 1 = (r 1 +r 4+r 6) S 2 =( r 2 +r 4+r 5) S 3 = (r 3+r 5+r 6) r 1 r 2 r 3 + r 4 r 5 + r 6 + S 1 S 2 S 3 e 1 r 1 + c 1 r 2 e 2 + c 2 r 3 e 3 + r 4 c 3 e 4 + e 5 r 5 c 4 www. assignmentpoint. com + e 6 r 6 c 5 + c 6

MATLAB Code Determine the parity check matrix, H and the generator matrix, G for a (7, 4) linear block encoder. n = 7; k = 4; gen = cyclpoly(n, k); %generator polynomial [H, G] = cyclgen(7, gen) %H is the parity check matrix and G is the generator matrix. The results of above code are, H= 1 0 0 G= 1 1 1 0 0 0 1 1 1 1 1 0 0 0 0 1 www. assignmentpoint. com

For the message sequence, m=1 0 0 1 determine code word. m = [1 0 0 1]; C = encode(m, 7, 4, 'Linear', G); C = transpose(C) The result of above code is, C=1 1 0 0 1 If the received sequence R=[1 1 0 0 1], determine syndrome and comment on the result. R = [1 1 0 0 1]; S = rem(R*transpose(H), 2) %Modulo-2 operation The result of above code is, S= 0 0 0 No error has occurred. If the received sequence R = [1 comment on the result. 1 1 1 0 www. assignmentpoint. com 0 1], determine syndrome and

R = [1 1 0 0 1]; S = rem(R*transpose(H), 2) %Modulo-2 operation The result of above code is, S= 0 0 1 Which is the third column of H, error has taken place on third bit of the codeword. www. assignmentpoint. com

The Cyclic Redundancy Check (CRC) www. assignmentpoint. com

Error Detection Coding Cyclic Redundancy Check It should be clear by now that a major goal in designing error detection algorithms is to maximize the probability of detecting errors using only a small number of redundant bits. Cyclic redundancy checks use some fairly powerful mathematics to achieve this goal. For example, an 8 -bit message consisting of the bits 10011010 corresponds to the polynomial, M(x) = 1×x 7 +0×x 6 + 0×x 5 +1×x 4 + 1×x 3 + 0×x 2 +1×x 1 + 0×x 0 = x 7 +x 4 + x 3 +x 1 www. assignmentpoint. com

For the purposes of calculating a CRC, a sender and receiver have to agree on a divisor or generator polynomial, G(x) is a polynomial of degree k. For example, G(x) = x 3 + x 2 + 1. In this case, k = 3. Common CRC polynomials CRC C(x) CRC-8 x 8 +x 2 +x + 1 CRC-10 x 10 + x 9 + x 5 +x 4 +x 1 +1 CRC-12 x 12 + x 11 +x 3 +x 2 +1 CRC-16 x 16 + x 15 +x 2 +1 CRC-CCITT x 16 + x 12 +x 5 +1 CRC-32 x 32 + x 26 +x 23 + x 22 +x 16 +x 12 + x 11+ x 10 +x 8 +x 7 +x 5 +x 4 +x 2 + x + 1 www. assignmentpoint. com

Steps of determining transmitted polynomial We wanted to create a polynomial T(x) for transmission that is derived from the original message M(x), is k bits longer than M(x), and is exactly divisible by G(x). We can do this in the following way: 1. Multiply M(x) by xk, that is, add k zeros at the end of the message. Call this zero-extended message xk M(x). 2. Divide xk M(x) by G(x) and find the remainder R(x). 3. Subtract the remainder from xk M(x) to get T(x). It should be obvious that what is left at this point is a message that is exactly divisible by G(x). www. assignmentpoint. com 40

Example-1 www. assignmentpoint. com

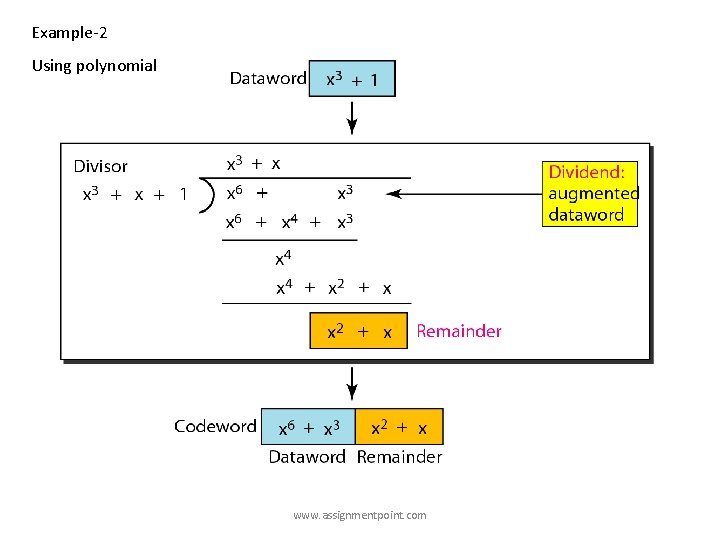
Example-2 Using polynomial www. assignmentpoint. com

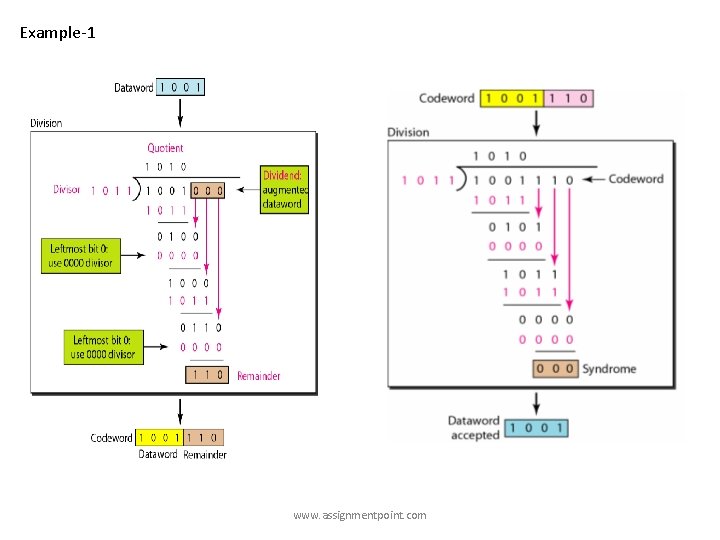
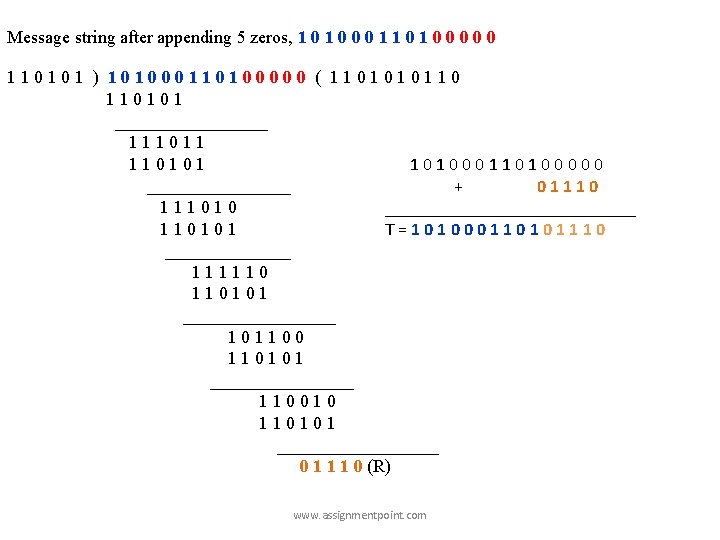
Example-3: Given, Message bit string Generator bit string Determine R(x) and T(x). M=1010001101 G=110101 (10 bits) (6 bits) Given, Message bit string, M = 1 0 0 0 1 1 0 1 (10 bits) Generator bit string, G = 1 1 0 1 (6 bits) Determine R(x) and T(x). Degree of G(x), r = 5. Message after appending 5 zeros, 101000110100000 The corresponding polynomial, www. assignmentpoint. com

www. assignmentpoint. com

Message string after appending 5 zeros, 1 0 0 0 110101 ) 101000110100000 ( 1101010110 110101 _________ 111011 110101 101000110100000 ________ + 0111010 ______________ 110101 T=101000110101110 _______ 111110 110101 _________ 101100 110101 ________ 110010 110101 _________ 0 1 1 1 0 (R) www. assignmentpoint. com

Transmitted bit sequences and polynomial T= 101000110101110 The received polynomial www. assignmentpoint. com

If there is some error at detecting end then polynomial of the received string will be, T(x) + E(x) where E(x) is arises from error. Now Choice of G(x): Here if E(x) is divisible by G(x) then error can’t be detected. To combat the situation, choosing of G(x) has some criteria like below. 1. One common type of error is a single-bit error, which can be expressed as E(x) = xi when it affects bit position i. If we select G(x) such that the first and the last term are nonzero, then we already have a two-term polynomial that cannot divide evenly into the one term E(x). www. assignmentpoint. com

2. For two bit error, ; m>r In this case G(x) has to be chosen such that it does not divide For example if then G(x) is unable to divide for k ≤ 32, 768. . 3. For odd number of bits in error then E(x) will contains odd number of terms. For 3 bit error, . If any polynomial has odd number of terms then it does not have any factor like (x+1). If G(x) has a factor of (x+1) it would be unable to divide E(x). www. assignmentpoint. com

4. For burst error of length k ≤ r then If the degree of G(x) is r and r ≥ k-1 then G(x) is simply unable to divide E(x). 5. If then length of the burst error k = r+1 and the burst is identical to G(x) then the CRC code is failed to detect error. The probability of such case, th term = (1/2)r+1 www. assignmentpoint. com

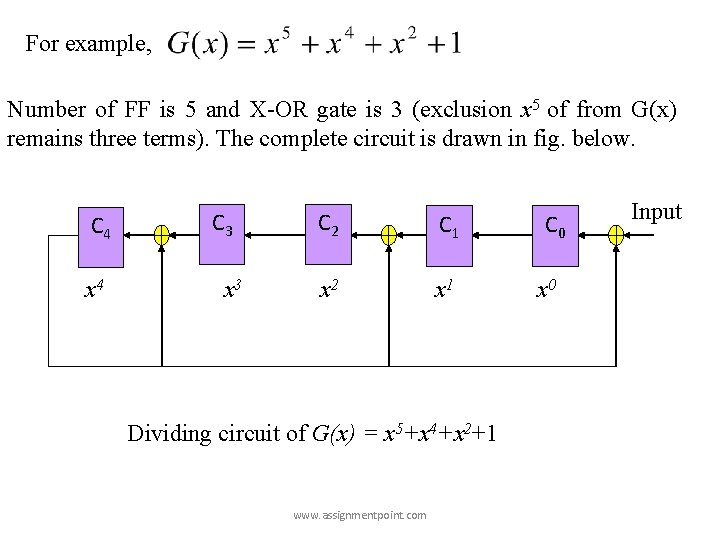
Dividing Circuit Design Division operation is done by a sequential digital circuit, consists of X-OR gates and a shift resister. Design procedure includes three steps. v. Number flip-flop of shift resister is equal to highest order of G(x) i. e. r. v. Maximum number X-OR gates could be r. v. Presence or absence of X-OR gate in the circuit after each flipflop depends upon presence / absence of terms of G(x) excluding xr. www. assignmentpoint. com

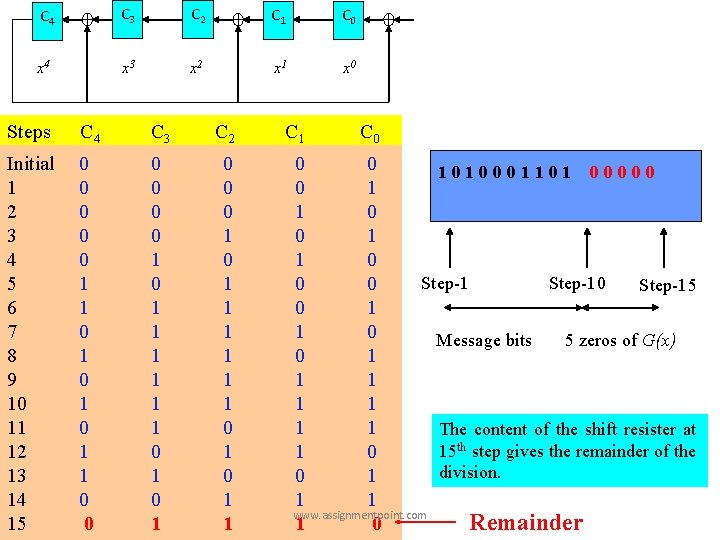
For example, Number of FF is 5 and X-OR gate is 3 (exclusion x 5 of from G(x) remains three terms). The complete circuit is drawn in fig. below. C 4 x 4 C 3 x 3 C 2 C 1 x 2 x 1 Dividing circuit of G(x) = x 5+x 4+x 2+1 www. assignmentpoint. com C 0 x 0 Input

C 4 C 3 C 2 C 1 C 0 x 4 x 3 x 2 x 1 x 0 Steps C 4 C 3 C 2 Initial 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 0 0 1 1 0 1 0 1 1 0 0 0 1 0 1 1 1 0 1 0 0 0 1 1 1 1 0 1 1 C 0 0 0 1010001101 00000 0 1 1 0 Step-10 0 0 Step-15 0 1 1 0 Message bits 5 zeros of G(x) 0 1 1 1 1 The content of the shift resister at 15 th step gives the remainder of the 1 0 division. 0 1 1 1 www. assignmentpoint. com 1 0 Remainder