Coding in noisy channel Source coding Channel coding

• Coding in noisy channel Source coding / Channel coding is to represent the source information in a manner that minimises the error probability in decoding into symbols. Symbol error / bit error is given as p, probability of an outcome per trial (per bit) in binomial distribution. Symbol error depends on what coding method is used. We want this to be small. This is achievable by error protection: -- improve tolerance of errors error detection: --- indicate occurrence of errors. Information ---- 6 1

c) 4 selections A compromise between two extremes 1. A lot of code words to give reasonable R. 2. Code words are as different as possible to reduce 3. p(e), e. g. A 00000 B 00111 C 11001 D 11110 Each code word differs from all the other in at least three digit positions. Hamming distance is the number of digits positions in which a pair of code words differ. Information ---- 6 2

Minimum Hamming distance (MHD) is the smallest hamming distance for the set of code words. MHD=3. One error can be tolerated. The example suggests that a compromise between low error rate and high data rate may be possible by using large group of digits, so that there a large number of possible code words, and by selecting a sufficient number for use to keep a reasonable R, but with codes words sufficiently different from each other to make p(e) acceptably low. Shannon’s Second Theorem Information ---- 6 3

Hamming distance A good channel code is designed so that, if a few errors occur in transmission, the output can still be identified with the correct input. This is possible because although incorrect, the output is sufficiently similar to the input to be recognisable. The idea of similarity is made more firm by the definition of a Hamming distance. Let X and Y be two binary sequences of the same length. The Hamming distance between these two codes is the number of symbols that disagree. Suppose the code X is transmitted over the channel. Due to errors, Y is received. The decoder will assign to Y the code X that minimises the Hamming distance between X and Y. Information ---- 6 4

If Y is received, and the decoder have a collection of codewords X 1, X 2, X 3, …, Then some of X (e. g. X 2) has This means that, Information ---- 6 5

For example, consider the codewords: a 10000 b 01100 c 00011 If the transmitter sends 10000 but there is a single bit error and the receiver gets 10001, it can be seen that the "nearest" codeword is in fact 10000 and so the correct codeword is found. It can be shown that to detect E bit errors, a coding scheme requires the use of codewords with a Hamming distance of at least E + 1. It can also be shown that to correct n bit errors requires a coding scheme with at least a Hamming distnace of 2 E + 1 between the codewords. By designing a good code, we try to ensure that the Hamming distance between possible codewords X is larger than the Hamming distance arising from errors. Information ---- 6 6

• Shannon’s Second Theorem If coding is in long groups of n binary digits, use only a small number M from the possible combinations. where C is the channel capacity. Assuming that the M selected code words are euiprobable, the information rate Information can be transmitted up to the and including the channel capacity without error (symbol errors in the decoded output) Unfortunately a large n can be unpractical. Information ---- 6 7

Example a) n=10, p=0. 01, C=0. 9 The maximum M Possible number of code words So 1 out of 2 code words are used. Error rate poor. b) n=100, p=0. 01, C=0. 9 So 1 out of 1024 code words are used. Error rate very good. But , which is an impractically large source alphabet &difficult to choose which code word to Information ---- 6 use. 8

• Practical codes for error detection and correction A set of code words with MHD=2, A single binary will produce a word not in the list, so that the error will be detected, but there will be no way of knowing which code was actually transmitted. This error can be however be corrected if the set of code words if MHD=3, to generate the nearest code word. In general To detect E errors MHD≥E+1 To correct E errors MHD≥ 2 E+1 (i) Block codes (n, k) n=total length of code k=number of information digits n-k=number of checking digits Information ---- 6 9

• Error detection i. Double-difference codes 0 11000 5 01010 1 10100 6 01001 2 10010 7 00110 3 10001 8 00101 4 01100 9 00011 MHD=2, single errors can be detected. A simple way of constructing such a code with n=5, is to use all the combinations in which exactly two “ 1”s appear known as “two out of five” code. (10 combinations) Alternatively, “ 3 out of 7” code with n=7, which has 35 combinations. Such systems can be arranged to automatically request retransmission of an incorrect symbol ARQ(automatic request repeat) Information ---- 6 10

• Parity codes Parity is the sum of binary digits- (even or odd), Parity digit is an extra digit added to make parity even or odd (as desired). Odd number of errors changes parity. The code will fail to detect an even number of error, but will detect any odd number of errors. Parity digit can be generated with exclusive ors e. g. with 3 info digits, parity digit is c=I 1⊕ I 2⊕ I 3 Code word is I 1 I 2 I 3 c Information ---- 6 11

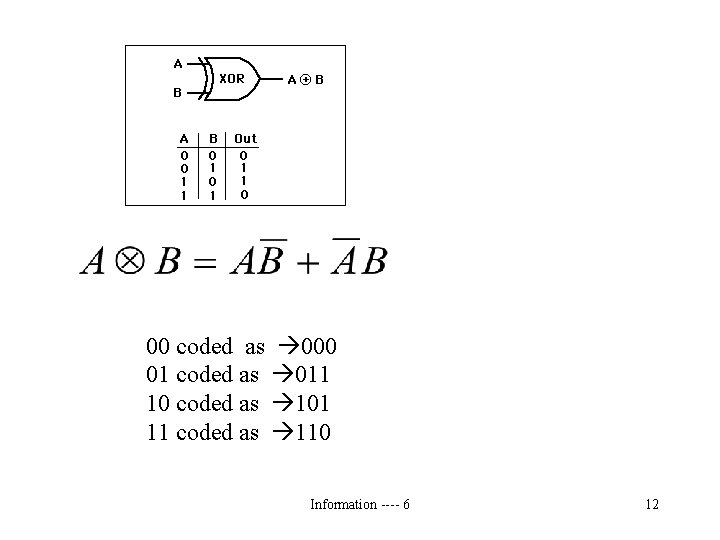
00 coded as 000 01 coded as 011 10 coded as 101 11 coded as 110 Information ---- 6 12

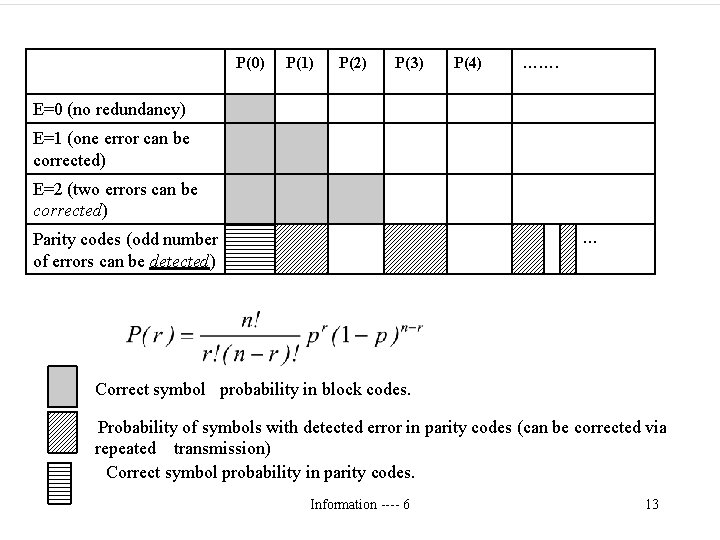
P(0) P(1) P(2) P(3) P(4) ……. E=0 (no redundancy) E=1 (one error can be corrected) E=2 (two errors can be corrected) … Parity codes (odd number of errors can be detected) Correct symbol probability in block codes. Probability of symbols with detected error in parity codes (can be corrected via repeated transmission) Correct symbol probability in parity codes. Information ---- 6 13

Homework: Sec. 3. 3. 4. problem 2, Solution: P 343. 2. (a) English text is to be transmitted via a binary symmetric channel that has a capacity of 50 binary digits per second a binary error probability of 0. 05. A non-redundant five-digit code is to be used for the symbols and punctuations (32 characters). Find the symbol error probability and comment on the quality of received text. (b) A single parity digit is added to the above five-digit code and the system arranged such that a detected error automatically leads to the immediate retransmission of that symbol until no error is detected. Find the symbol error probability and the effective rate of transmission of symbols, and comment on the quality of the received text. Information ---- 6 14