Graph Theory Graph theory is the study of

Graph Theory Graph theory is the study of the properties of graph structures. It provides us with a language with which to talk about graphs.

Degree • The degree of a vertex is the number of edges incident upon it. • The sum of the vertex degrees in any undirected graph is even (twice the number of edges). • Every graph contains an even number of odd-degree vertices.

Connectivity • A graph is connected if there is an undirected path between every pair of vertices. • The existence of a spanning tree is sufficient to prove connectivity. • The vertex (edge) connectivity is the smallest number of vertices (edges) which must be deleted to disconnect the graph.

Some terms • articulation vertex biconnected • bridge edge-biconnected • Testing for articulation vertices or bridges is easy via brute force.

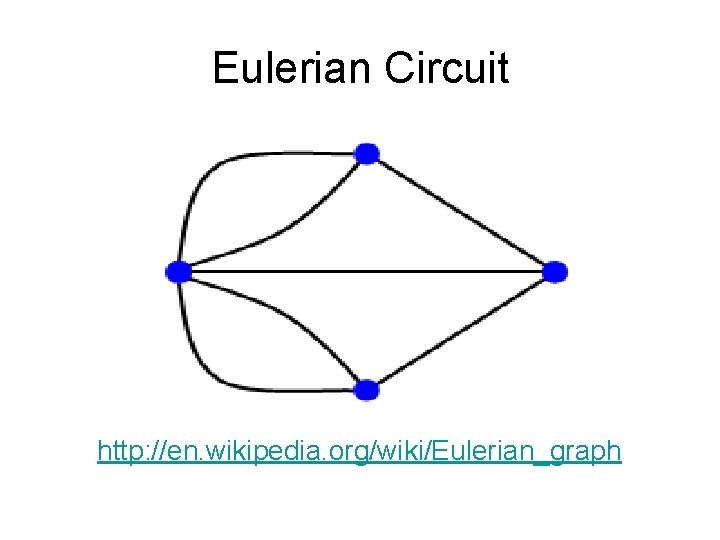
Cycles • Eulerian cycle (path): a tour which visits every edge of the graph exactly once. • Actually, it is a circuit, not a cycle, because it may visit vertices more than once. • A mailman’s route is ideally an Eulerian cycle, so he can visit every street (edge) in the neighborhood once before returning home.

Eulerian Circuit http: //en. wikipedia. org/wiki/Eulerian_graph

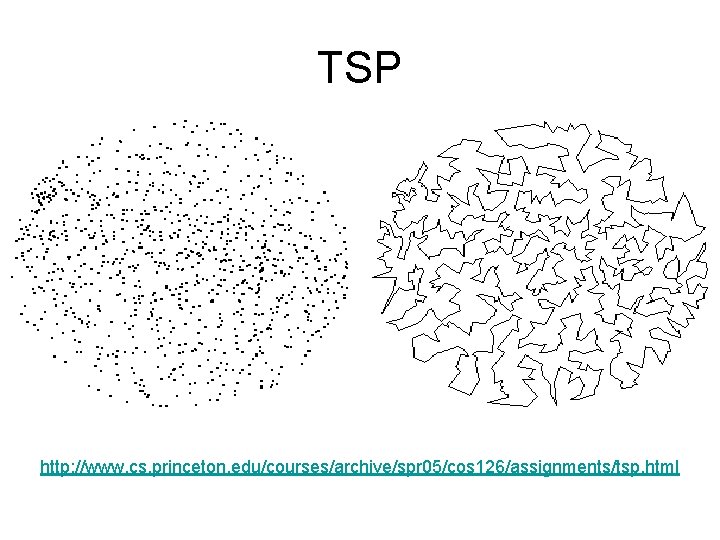
• An undirected graph contains an Eulerian cycle if it is connected and every vertex is of even degree. • A Hamiltonian cycle is a tour which visits every vertex of the graph exactly once. • The traveling salesman problem asks for the shortest such tour on a weighted graph.

TSP http: //www. cs. princeton. edu/courses/archive/spr 05/cos 126/assignments/tsp. html

Planer Graph • Euler’s formula: n-m+f=2 • • • n: # of vertices m: # of edges f: # of faces Trees: m=n-1, f=1 Cubes: n=8, m=12, f=6

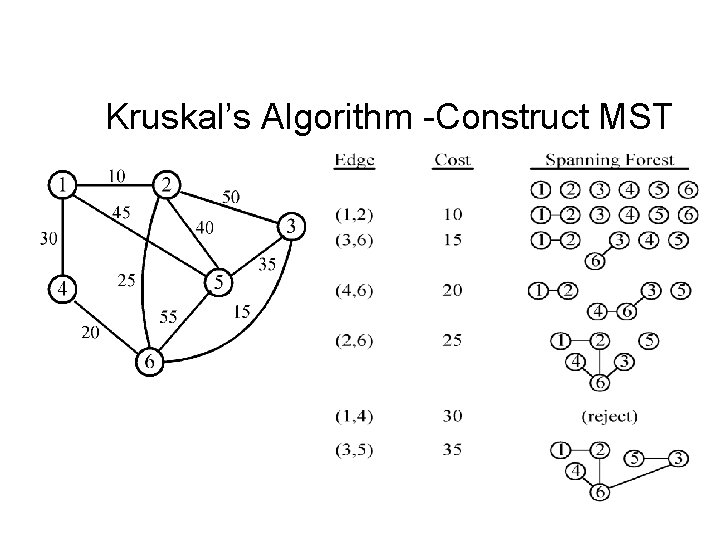
MST • Kruskal’s algorithm: starting from a minimal edge • Prim’s algorithm: starting from a given vertex – How about maximum spanning tree – and Minimum Product spanning tree

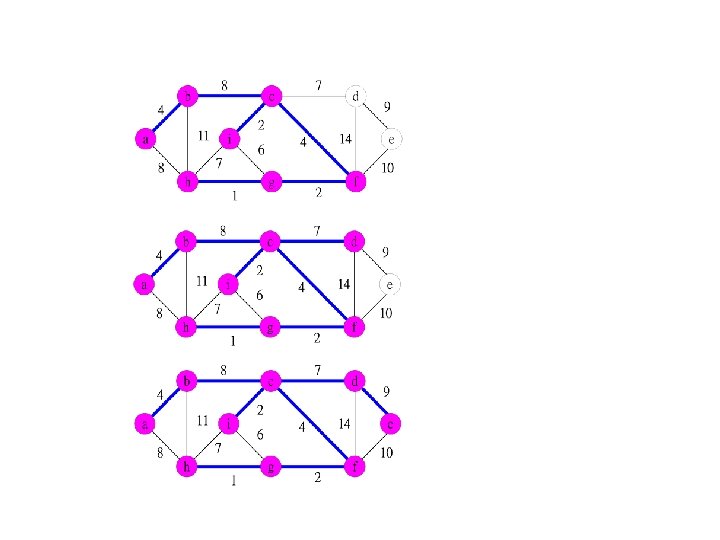
Kruskal’s Algorithm • Algorithm Kruskal(G) • Input：G=(V, E)為無向加權圖(undirected weighted graph)， 其中V={v 0, …, vn-1} • Output：G的最小含括樹(minimum spanning tree, MST) • T← //T為MST，一開始設為空集合 • while T包含少於n-1個邊 do • 選出邊(u, v)，其中(u, v) E，且(u, v)的加權(weight)最小 • E←E-(u, v) • if ( (u, v)加入T中形成循環(cycle) ) then 將(u, v)丟棄 • else T←T (u, v) • return T

Kruskal’s Algorithm -Construct MST

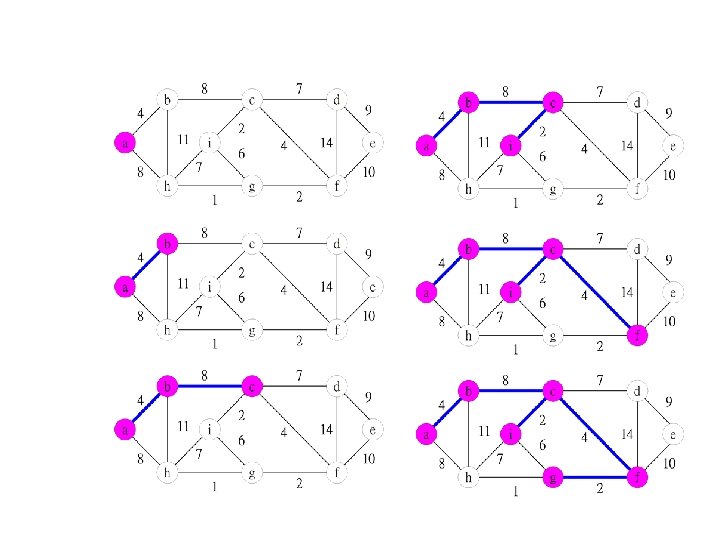
Prim’s algorithm • Algorithm Prim(G) • Input：G=(V, E)為無向加權圖(undirected weighted graph)，其 中V={v 0, …, vn-1} • Output：G的最小含括樹(minimum spanning tree, MST) • T← //T為MST，一開始設為空集合 • X←{vx} //隨意選擇一個頂點vx加入集合X中 • while T包含少於n-1個邊 do • 選出(u, v) E，其中u X且v V-X，且(u, v)的加權(weight)最小 • T←T (u, v) • X←X {v} • return T

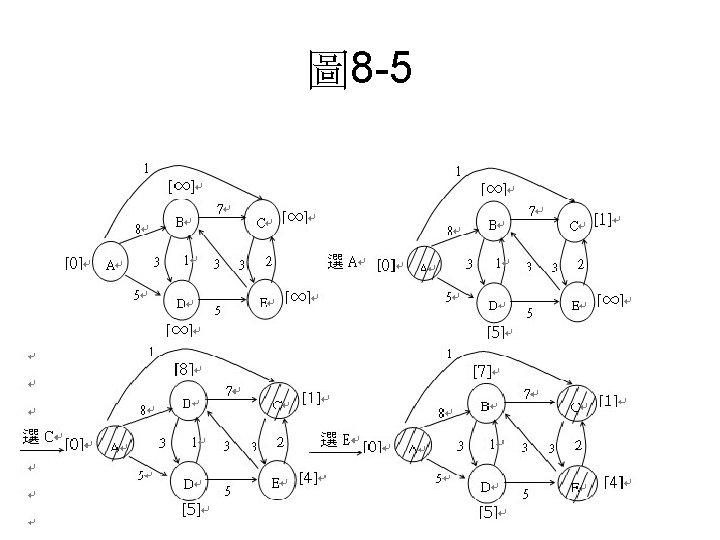
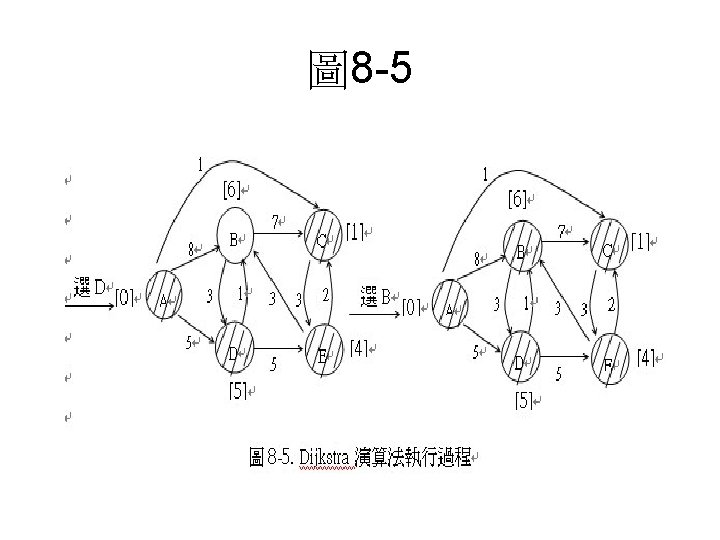
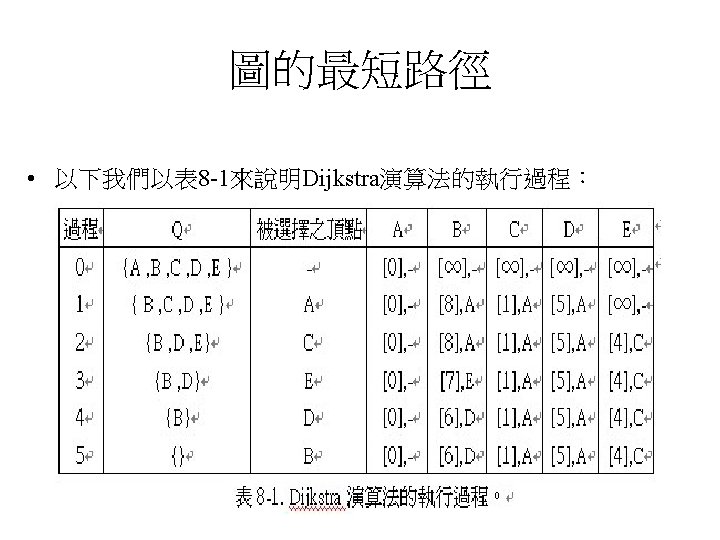
One-to-all shorted path • Dijkstra演算法: Dijkstra演算法屬於求取單一來源(source)至所有目 標(destination)頂點的一至多(one-to-all)最短路徑演算法

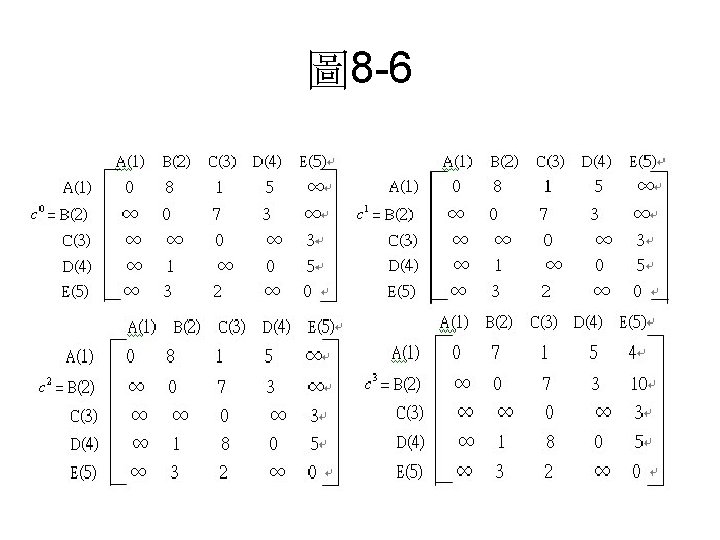
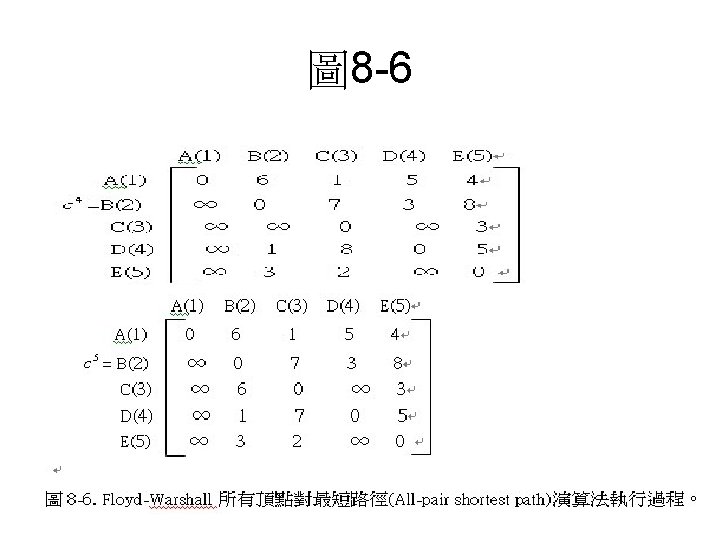
All-pair shortest path • Floyd-Warshall的所有頂點對最短路徑(all-pair shortest path)演 算法：