Introduction to Graph Definition of Graph A graph

Introduction to Graph

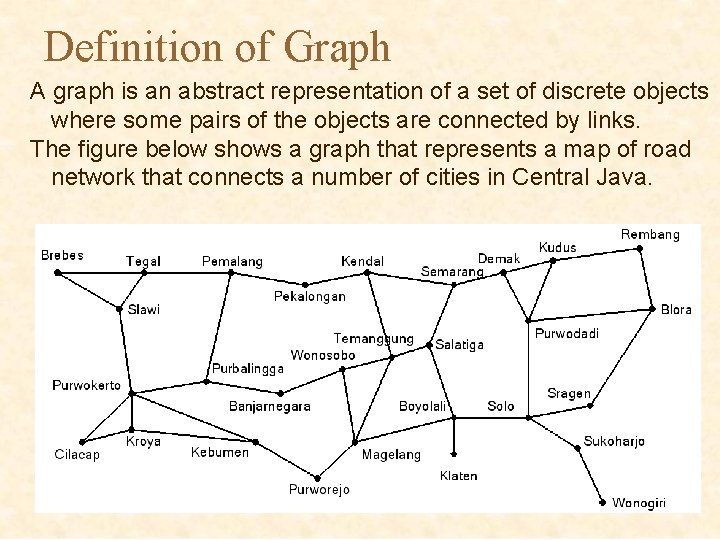
Definition of Graph A graph is an abstract representation of a set of discrete objects where some pairs of the objects are connected by links. The figure below shows a graph that represents a map of road network that connects a number of cities in Central Java.

Bridges of Königsberg (Euler, 1736) Can someone pass every bridge exactly once and come back the his/her original position? A graph can be used to represent the Königsberg bridge: Vertex represents a dry land Arc or edge represents a bridge

Graph Representation Graph G = (V, E) where: V = Set of vertices, may not be a null set = {v 1, v 2, . . . , vn} E = Set of edges, each connecting a pair of vertices = {e 1, e 2, . . . , en}

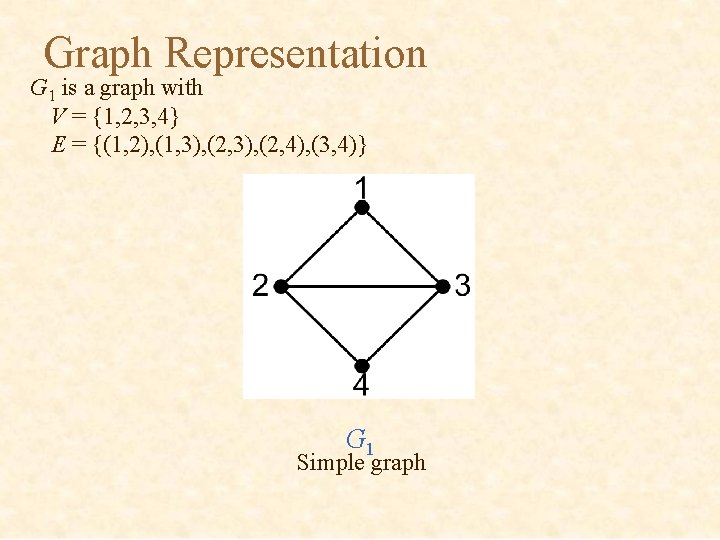
Graph Representation G 1 is a graph with V = {1, 2, 3, 4} E = {(1, 2), (1, 3), (2, 4), (3, 4)} G 1 Simple graph

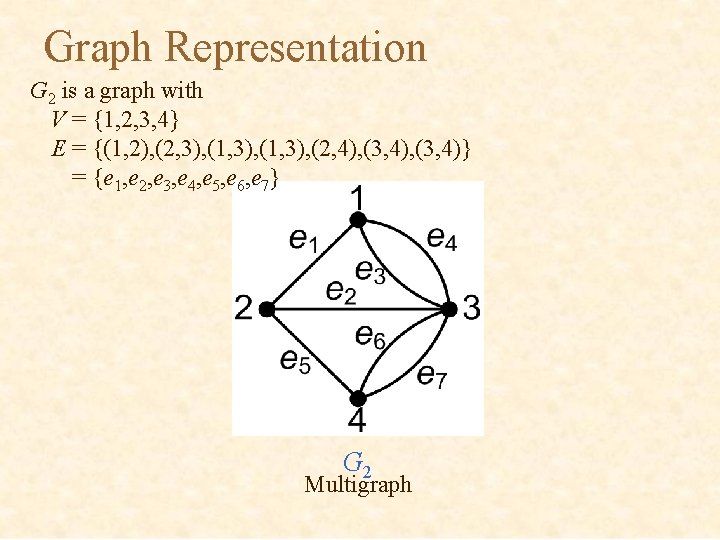
Graph Representation G 2 is a graph with V = {1, 2, 3, 4} E = {(1, 2), (2, 3), (1, 3), (2, 4), (3, 4)} = {e 1, e 2, e 3, e 4, e 5, e 6, e 7} G 2 Multigraph

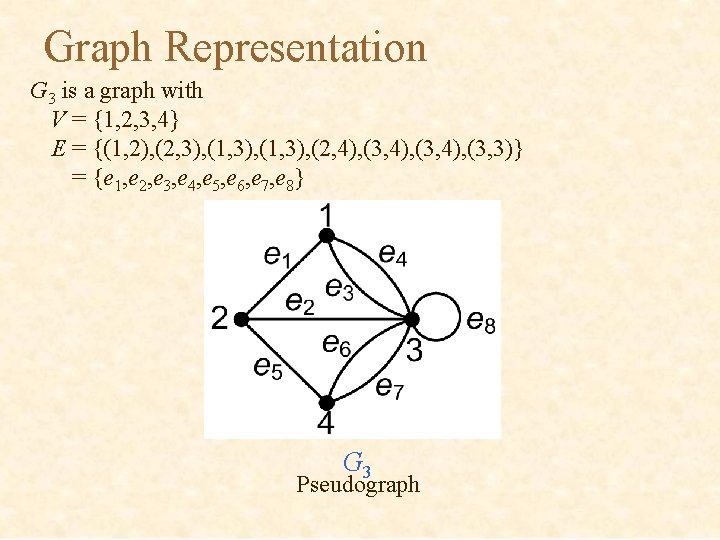
Graph Representation G 3 is a graph with V = {1, 2, 3, 4} E = {(1, 2), (2, 3), (1, 3), (2, 4), (3, 3)} = {e 1, e 2, e 3, e 4, e 5, e 6, e 7, e 8} G 3 Pseudograph

Graph Classification Based on the existence of loop or multiple edges, a graph can be classified into: 1. Simple graph, if the graph does not have any loop or double edge. 2. Unsimple graph, if the graph has any loop or double edge.

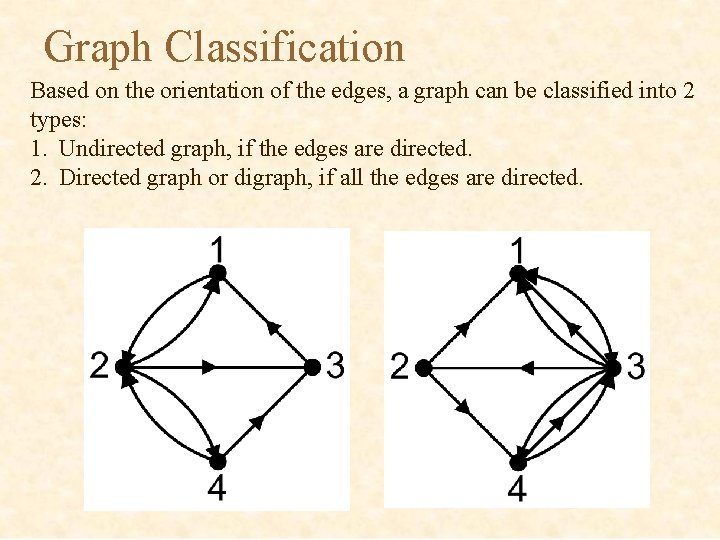
Graph Classification Based on the orientation of the edges, a graph can be classified into 2 types: 1. Undirected graph, if the edges are directed. 2. Directed graph or digraph, if all the edges are directed.

Graph Terminology 1. Adjacency Two vertices are said to be adjacent if they are directly connected through an edge. Observe graph G 1: Vertex 1 is adjacent with vertex 2 and 3. Vertex 1 is not adjacent to vertex 4. G 1

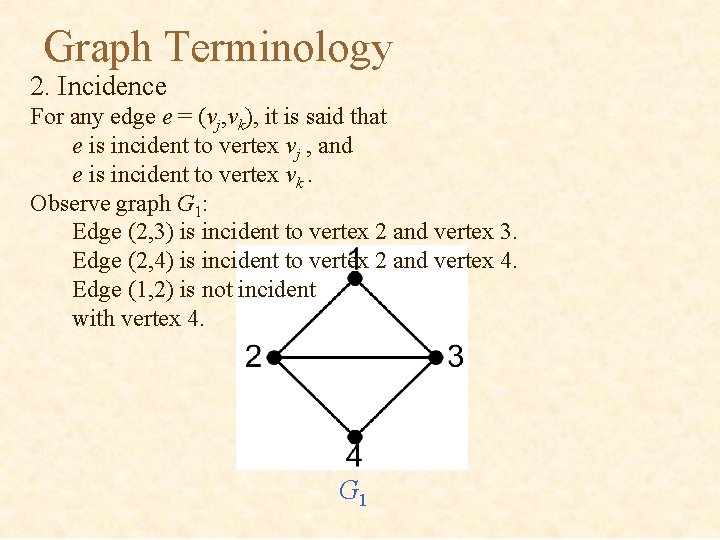
Graph Terminology 2. Incidence For any edge e = (vj, vk), it is said that e is incident to vertex vj , and e is incident to vertex vk. Observe graph G 1: Edge (2, 3) is incident to vertex 2 and vertex 3. Edge (2, 4) is incident to vertex 2 and vertex 4. Edge (1, 2) is not incident with vertex 4. G 1

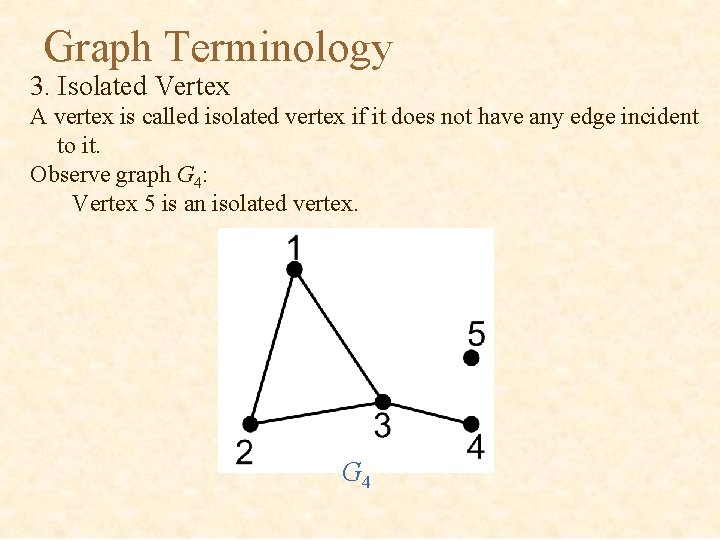
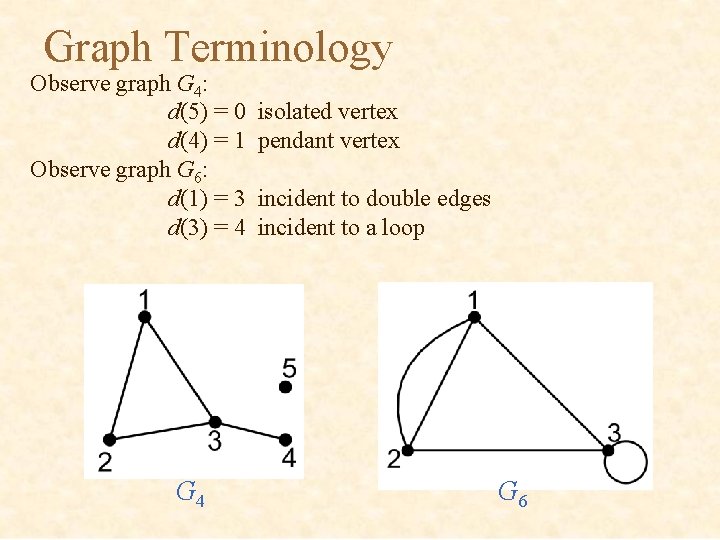
Graph Terminology 3. Isolated Vertex A vertex is called isolated vertex if it does not have any edge incident to it. Observe graph G 4: Vertex 5 is an isolated vertex. G 4

Graph Terminology 4. Empty Graph (Null Graph) An empty graph is a graph whose set of edges is a null set. Observe graph G 5: It is an empty graph (null graph). G 5

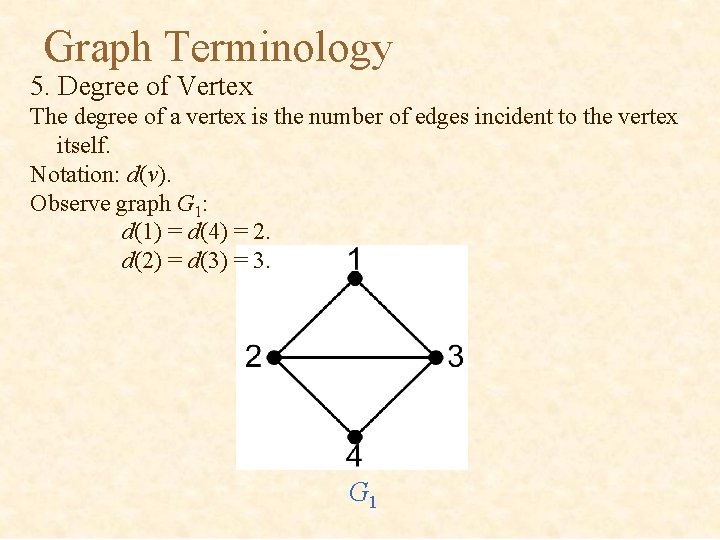
Graph Terminology 5. Degree of Vertex The degree of a vertex is the number of edges incident to the vertex itself. Notation: d(v). Observe graph G 1: d(1) = d(4) = 2. d(2) = d(3) = 3. G 1

Graph Terminology Observe graph G 4: d(5) = 0 d(4) = 1 Observe graph G 6: d(1) = 3 d(3) = 4 G 4 isolated vertex pendant vertex incident to double edges incident to a loop G 6

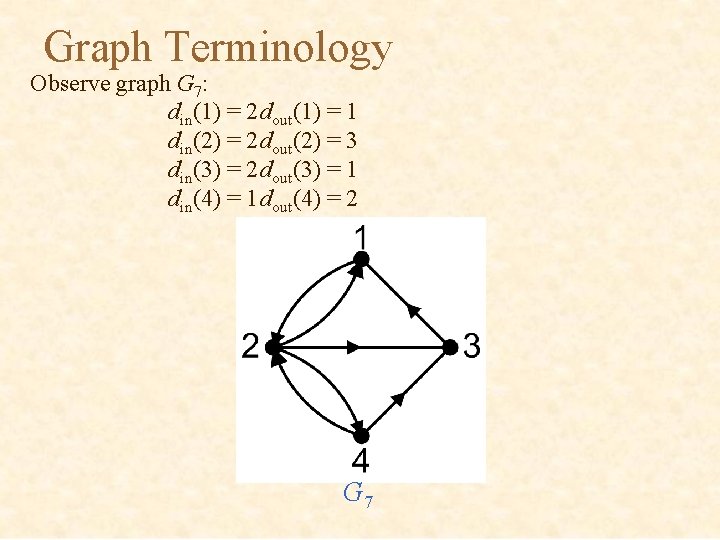
Graph Terminology In a directed graph: din(v) = in-degree = number of arcs arriving to a vertex dout(v) = out-degree = number of arcs departing from a vertex d(v) = din(v) + dout(v)

Graph Terminology Observe graph G 7: din(1) = 2 dout(1) = 1 din(2) = 2 dout(2) = 3 din(3) = 2 dout(3) = 1 din(4) = 1 dout(4) = 2 G 7

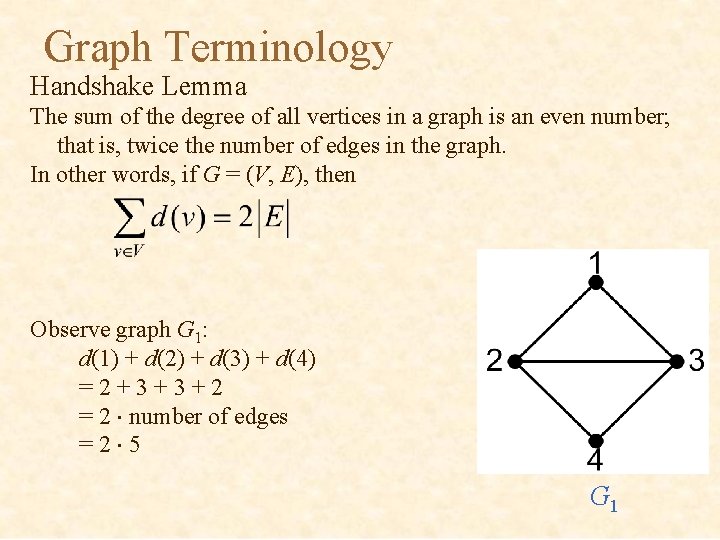
Graph Terminology Handshake Lemma The sum of the degree of all vertices in a graph is an even number; that is, twice the number of edges in the graph. In other words, if G = (V, E), then Observe graph G 1: d(1) + d(2) + d(3) + d(4) =2+3+3+2 = 2 number of edges =2 5 G 1

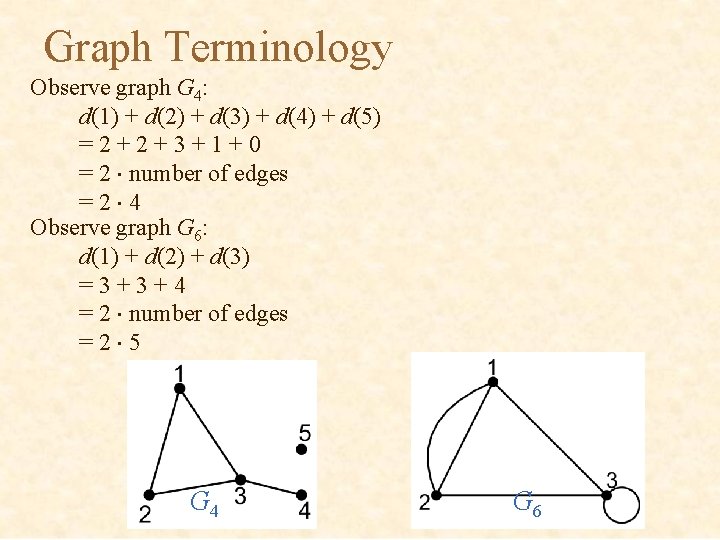
Graph Terminology Observe graph G 4: d(1) + d(2) + d(3) + d(4) + d(5) =2+2+3+1+0 = 2 number of edges =2 4 Observe graph G 6: d(1) + d(2) + d(3) =3+3+4 = 2 number of edges =2 5 G 4 G 6

Graph Terminology Example: A graph has five vertices. Can you draw the graph if the degree of the vertices are: (a) 2, 3, 1, 1, and 2? (b) 2, 3, 3, 4, and 4? Solution: (a) No, because 2 + 3 + 1 + 2 = 9, is an odd number. (b) Yes, because 2 + 3 + 4 = 16, is an even number.

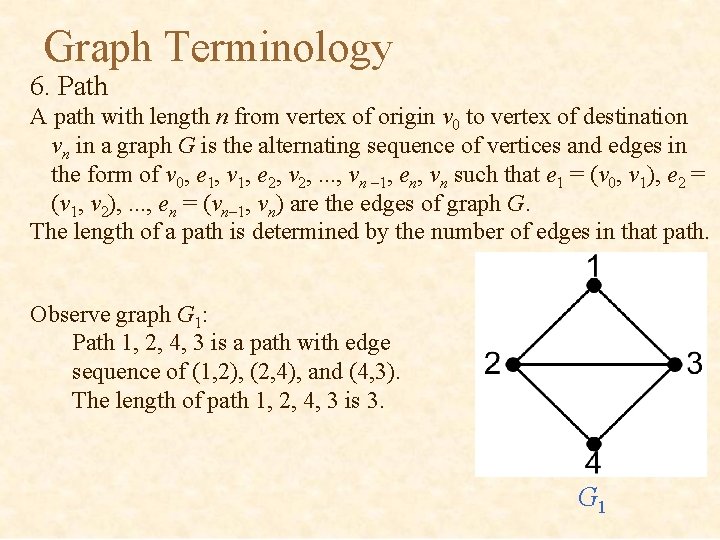
Graph Terminology 6. Path A path with length n from vertex of origin v 0 to vertex of destination vn in a graph G is the alternating sequence of vertices and edges in the form of v 0, e 1, v 1, e 2, v 2, . . . , vn – 1, en, vn such that e 1 = (v 0, v 1), e 2 = (v 1, v 2), . . . , en = (vn– 1, vn) are the edges of graph G. The length of a path is determined by the number of edges in that path. Observe graph G 1: Path 1, 2, 4, 3 is a path with edge sequence of (1, 2), (2, 4), and (4, 3). The length of path 1, 2, 4, 3 is 3. G 1

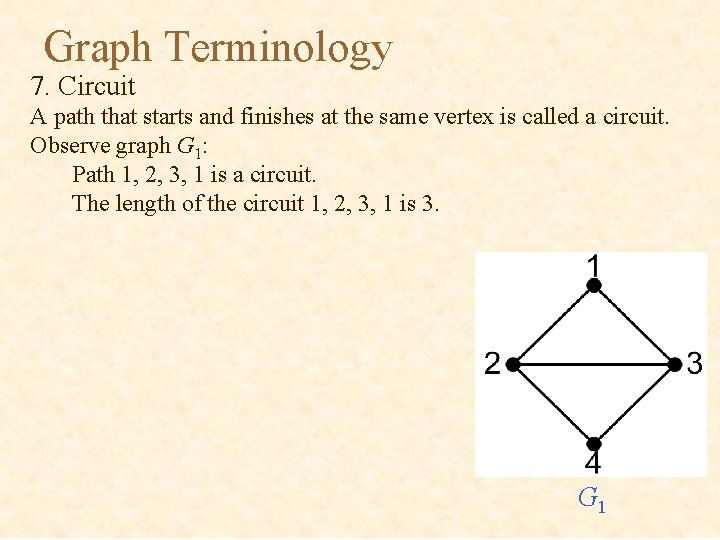
Graph Terminology 7. Circuit A path that starts and finishes at the same vertex is called a circuit. Observe graph G 1: Path 1, 2, 3, 1 is a circuit. The length of the circuit 1, 2, 3, 1 is 3. G 1

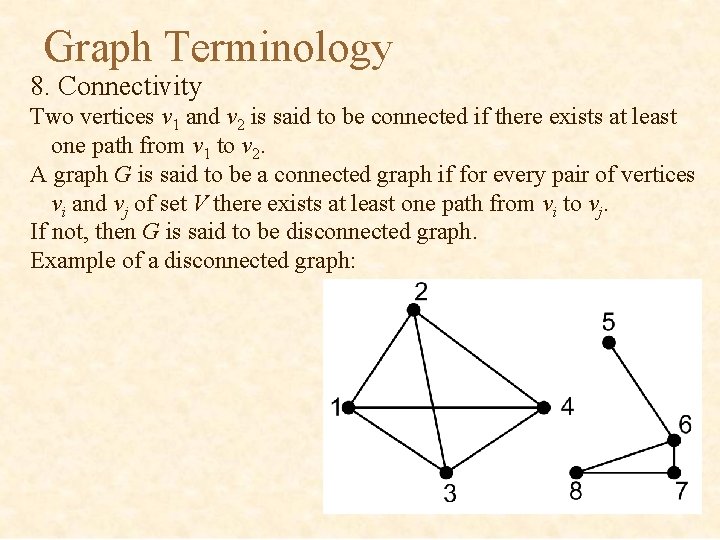
Graph Terminology 8. Connectivity Two vertices v 1 and v 2 is said to be connected if there exists at least one path from v 1 to v 2. A graph G is said to be a connected graph if for every pair of vertices vi and vj of set V there exists at least one path from vi to vj. If not, then G is said to be disconnected graph. Example of a disconnected graph:

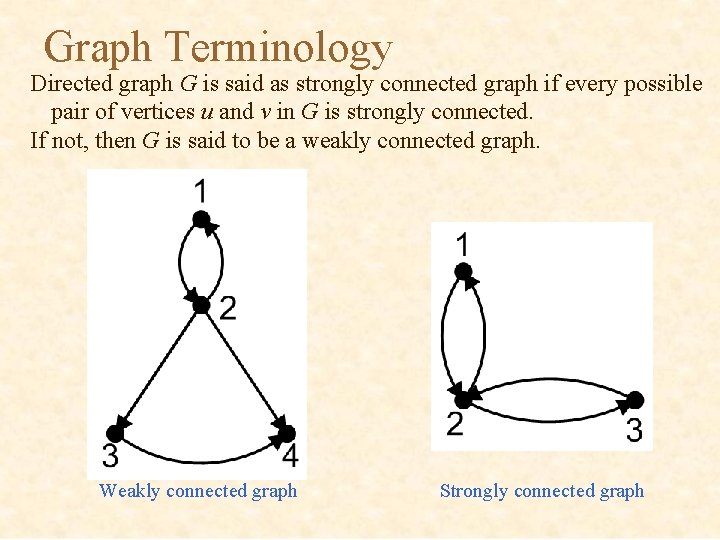
Graph Terminology A directed graph G is said to be connected if its non-directed graph is connected (Note: the non-directed graph of a directed graph G is obtained by omitting all arrow heads). Two vertices, u and v, in a directed graph G are said as strongly connected vertices if there exists a directed path from u to v and also from v to u. If u and v are not strongly connected vertices but the non-directed graph of G is a connected one, then u and v are said as weakly connected vertices.

Graph Terminology Directed graph G is said as strongly connected graph if every possible pair of vertices u and v in G is strongly connected. If not, then G is said to be a weakly connected graph. Weakly connected graph Strongly connected graph

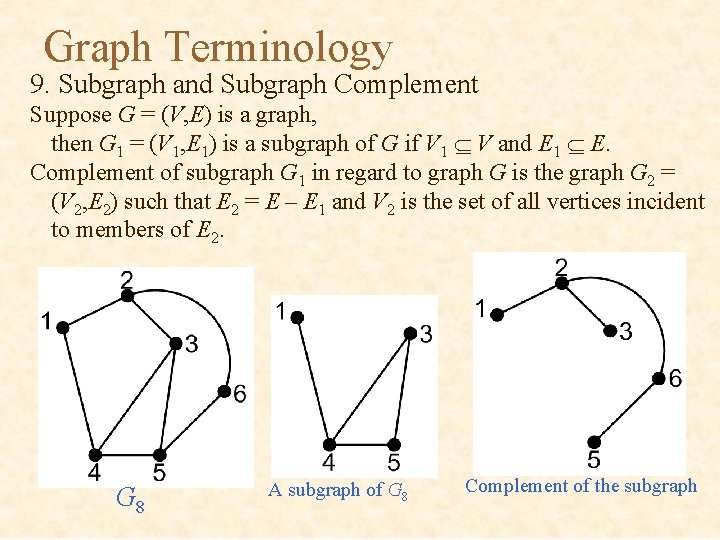
Graph Terminology 9. Subgraph and Subgraph Complement Suppose G = (V, E) is a graph, then G 1 = (V 1, E 1) is a subgraph of G if V 1 V and E 1 E. Complement of subgraph G 1 in regard to graph G is the graph G 2 = (V 2, E 2) such that E 2 = E – E 1 and V 2 is the set of all vertices incident to members of E 2. G 8 A subgraph of G 8 Complement of the subgraph

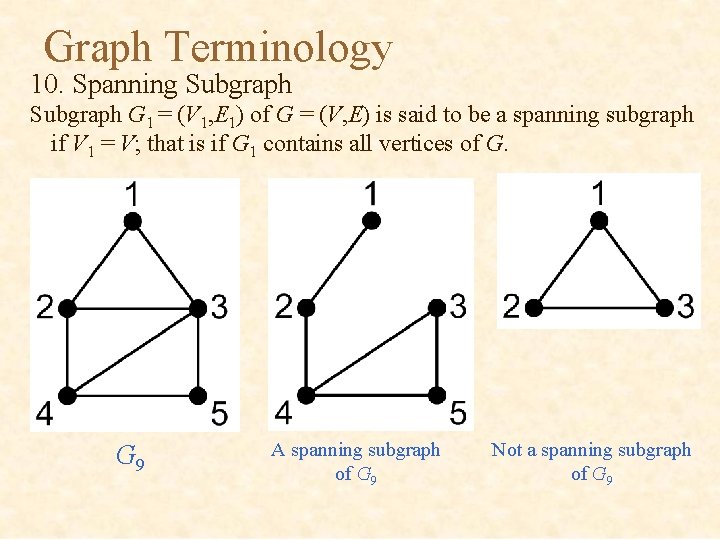
Graph Terminology 10. Spanning Subgraph G 1 = (V 1, E 1) of G = (V, E) is said to be a spanning subgraph if V 1 = V; that is if G 1 contains all vertices of G. G 9 A spanning subgraph of G 9 Not a spanning subgraph of G 9

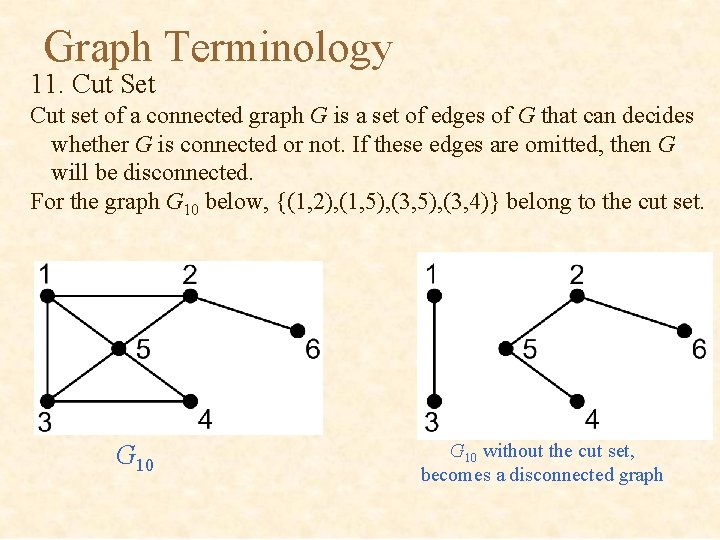
Graph Terminology 11. Cut Set Cut set of a connected graph G is a set of edges of G that can decides whether G is connected or not. If these edges are omitted, then G will be disconnected. For the graph G 10 below, {(1, 2), (1, 5), (3, 4)} belong to the cut set. G 10 without the cut set, becomes a disconnected graph

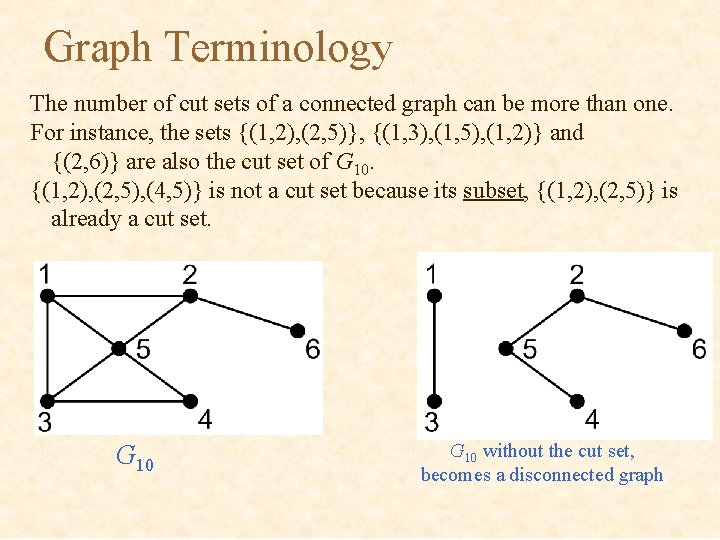
Graph Terminology The number of cut sets of a connected graph can be more than one. For instance, the sets {(1, 2), (2, 5)}, {(1, 3), (1, 5), (1, 2)} and {(2, 6)} are also the cut set of G 10. {(1, 2), (2, 5), (4, 5)} is not a cut set because its subset, {(1, 2), (2, 5)} is already a cut set. G 10 without the cut set, becomes a disconnected graph

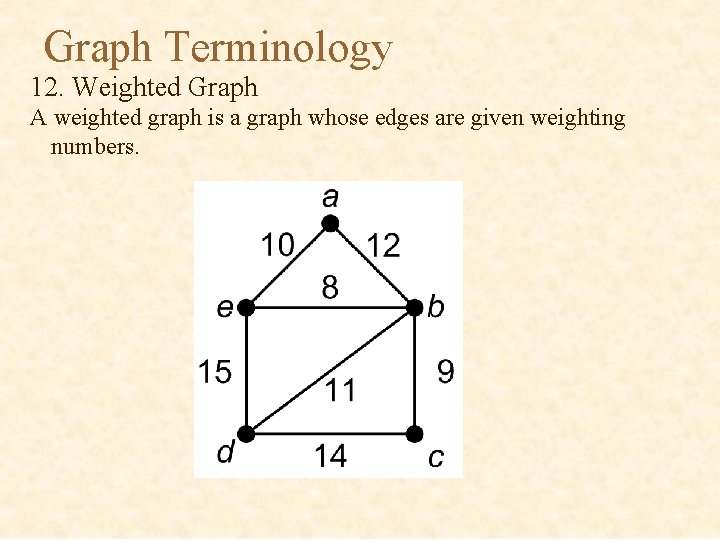
Graph Terminology 12. Weighted Graph A weighted graph is a graph whose edges are given weighting numbers.

Homework 9 Graph G is given by the figure below. (a) List all possible paths from A to C. (b) List all possible circuits. (c) Write down at least 4 cut sets of the graph. (d) Draw the subgraph G 1 = {B, C, X, Y}. (e) Draw the complement of subgraph G 1. Graph G

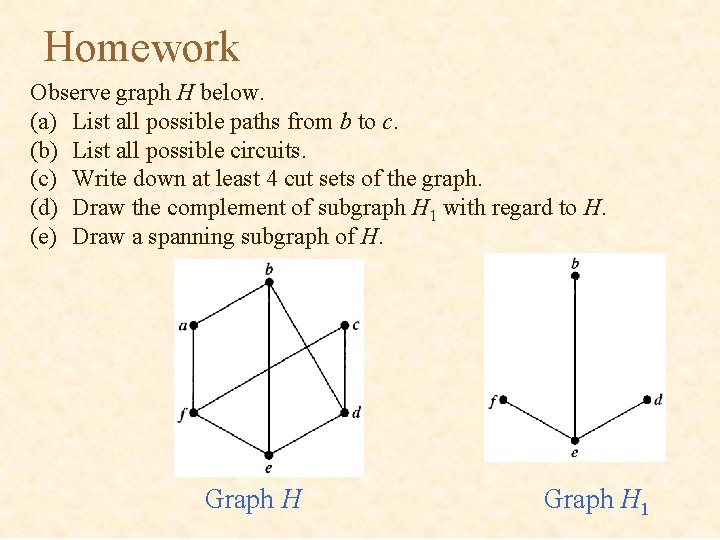
Homework Observe graph H below. (a) List all possible paths from b to c. (b) List all possible circuits. (c) Write down at least 4 cut sets of the graph. (d) Draw the complement of subgraph H 1 with regard to H. (e) Draw a spanning subgraph of H. Graph H 1