Spectral Graph Theory and Applications Advanced Course WS

Spectral Graph Theory and Applications Advanced Course WS 2011/2012 Thomas Sauerwald He Sun Max Planck Institute for Informatics

Course Information • Time: Wednesday 2: 15 PM – 4: 00 PM • Location: Room 024, MPI Building • Credit: 5 credit points • Lecturers: Thomas Sauerwald, He Sun • Office Hour: Wednesday 10: 00 AM – 11: 00 AM • Prerequisites: Basic knowledge of discrete mathematics and linear algebra • Lecture notes: See homepage for weekly update • Homepage: http: //www. mpi-inf. mpg. de/departments/d 1/teaching/ws 11/SGT/index. html 2/25

Course Information (contd. ) • Grading – Homework (3 problem sets) – You need to collect at least 40% of the homework points to be eligible to take the exam. – The final exam will be based on the homework and lectures. 3/25

Topics Max Cut Approximation Algorithms Expanders Pseudorandomness The Unified Theory Random Walks Cheeger Inequality Eigenvalues Complexity 4/25

Why do you need this course? • Provides a powerful tool for designing randomized algorithms. • Gives the basics of Markov chain theory. • Covers some of the most important results in the past decade, e. g. derandomization of log-space complexity class. • Nicely combines classical graph theory with modern mathematics (geometry, algebra, etc). 5/25

Lecture 1 INTRODUCTION 6/25

Seven Bridges of Königsberg, 1736 L. Euler(1707 -1783) 7/25

From then on. . . • Connectivity • Chromatic number • Euler Path • Hamiltonian Path • Matching • Graph homomorphism 8/25

About 50 years ago. . . 9/25

Magic graphs: Expanders • Combinatorically, expanders are highly connected graphs, i. e. , to disconnect a large part of the graph, one has to remove many edges. • Geometrically, every vertex set has a large boundary. • Probabilistically, expanders are graphs whose behavior is “like” random graphs. • Algebraically, expanders correspond to real-symmetric matrices whose first positive eigenvalue of the Laplacian matrix is bounded away from zero. 10/25

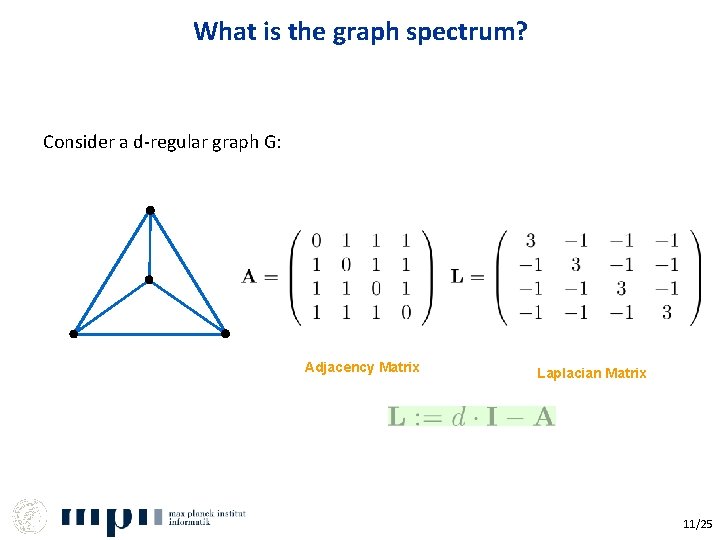
What is the graph spectrum? Consider a d-regular graph G: Adjacency Matrix Laplacian Matrix 11/25

What is the graph spectrum? (contd. ) • If A is a real symmetric matrix, then all the eigenvalues are real. • Moreover, if G is a d-regular graph, then We call . the spectrum of graph G. 12/25

Applications of graph spectrum In Computer Science In Mathematics • Pseudorandomness • Graph theory • Circuit complexity • Group theory • Network design • Number theory • Approximation algorithms • Algebra 13/25

Example 1: Super concentrators There is a long and still ongoing search for super concentrators with n inputs and output vertices and Kn edges with K as small as possible. This “sport” has motivated quite a few important advances in this area. The current “world record” holders are Alon and Capalbo. S. Hoory et al. In: Bulletin of American Mathematical Society, 2006. 14/25

Finally, the super concentrators constructed by Valiant in the context of computational complexity established the fundamental role of expander graphs in computation. 2010 ACM Turing Award Citation 15/25

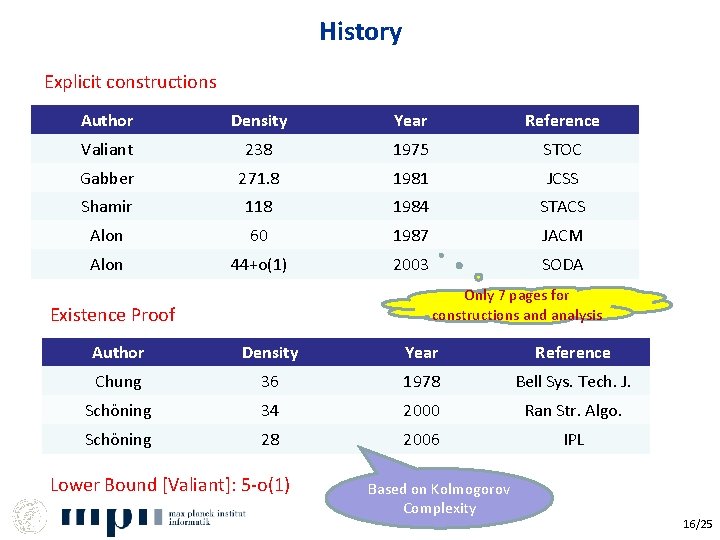
History Explicit constructions Author Density Year Reference Valiant 238 1975 STOC Gabber 271. 8 1981 JCSS Shamir 118 1984 STACS Alon 60 1987 JACM Alon 44+o(1) 2003 SODA Only 7 pages for constructions and analysis Existence Proof Author Density Year Reference Chung 36 1978 Bell Sys. Tech. J. Schöning 34 2000 Ran Str. Algo. Schöning 28 2006 IPL Lower Bound [Valiant]: 5 -o(1) Based on Kolmogorov Complexity 16/25

Example 2: Graph Partitioning Applications • Community detection • Graph partitioning • Machine learning 17/25

Example 3: Ramanujan Graphs Ramanujan graphs are graphs having the best expansion ratio. 18/25

Ramanujan graphs Big Open Problem: Construct Ramanujan graphs with any degree. 19/25

Example 4: Random walks Applications • Simulation of physical phenomenon • Information spreading on social networks • Approximation of counting problems • Hardness amplification G. Pólya (1887 -1985) 20/25

Example 4: Random walks Theorem (Pólya, 1921) Consider a random walk on an infinite D-dimensional grid. If D = 2, then with probability 1, the walk returns to the starting point an infinite number of times. If D > 2, then with probability 1, the walk returns to the starting point only a finite number of times. A drunk man will eventually return home but a drunk bird will lose its way in space. 21/25

What a random walk! Interviewed on his 90 th birthday Pólya stated, "I started studying law, but this I could stand just for one semester. I couldn't stand more. Then I studied languages and literature for two years. After two years I passed an examination with the result I have a teaching certificate for Latin and Hungarian for the lower classes of the gymnasium, for kids from 10 to 14. I never made use of this teaching certificate. And then I came to philosophy, physics, and mathematics. In fact, I came to mathematics indirectly. I was really more interested in physics and philosophy and thought about those. It is a little shortened but not quite wrong to say: I thought I am not good enough for physics and I am too good for philosophy. Mathematics is in between. " (Alexanderson, 1979) 22/25

Example 5: Randomness Complexity From Art to Science 141592653589793238462643383279502884197169399375105820974944592307816406286208998628 034825342117067982148086513282306647093844609550582231725359408128481117450284102701 938521105559644622948954930381964428810975665933446128475648233786783165271201909145 648566923460348610454326648213393607260249141273724587006606315588174881520920962829 2540 23/25

Example 5: Randomness Complexity From Art to Science A. N. Kolmogorov (1903 -1987) Andrew Yao (1946 - ) 24/25

Example 5: Randomness Complexity From Art to Science Generate “almost random” sequences using modern computers. 25/25