6 Graph 1 Graph q Graph jmleewww hansung

6장 Graph 1

Graph의 개요 q Graph의 이용 해결하여야 하는 문제 jmlee@www. hansung. ac. kr Modeling Graphs Solve 3

Graph에서의 용어 q q q Vertex: Node Edge: Link Graph: Vertex와 Edge의 집합 m G=(V, E) m Vertex의 집합: V(G) m Edge의 집합: E(V) 0 2 1 3 m V(G)= {0, 1, 2, 3} m E(G)={ (0, 1), (0, 2), (0, 3), (1, 2), (1, 3), , {2, 3)} jmlee@www. hansung. ac. kr 4

Graph에서의 용어 q Undirected Graph m edge의 표시: (vi, vj) or (vj, vi) q Directed Graph: Edge에 방향이 있음 m edge의 표시: <vi, vj> <> <vj, vi> 0 1 m V(G)={0, 1, 2} m E(G)={<0, 1>, <1, 0>, <1. 2>} q 2 특수 Graph: P 264, 그림 6. 3 m Self Loop Graph m Multi Graph jmlee@www. hansung. ac. kr 5

Graph에서의 용어 q 완전 Graph(Complete Graph) m 하나의 Vertex는 자신을 제외한 모든 Vertext에 Edge가 있는 경우 m n개의 Vertx로 구성된 CG의 edge의 수 n (n-1)n/2 m 방향 그래프의 경우: n(n-1) jmlee@www. hansung. ac. kr 6

Graph에서의 용어 q Adjacent Vertex m (vi, vj)가 있으면 vi와 vj는 Adjacent하다고 함 v 2 v 1 e 2 e 4 v 4 e 3 v 3 e 5 e 6 e 7 (v 1, v 2) (v 1, v 4) (v 1, v 3) v 5 E 7은 (v 4, v 5)에 incident 함 q Incident Edge m vi, vj사이에 Edge가 있으면 그 Edge는 vi, vj에 Incident하다고 함 jmlee@www. hansung. ac. kr 7

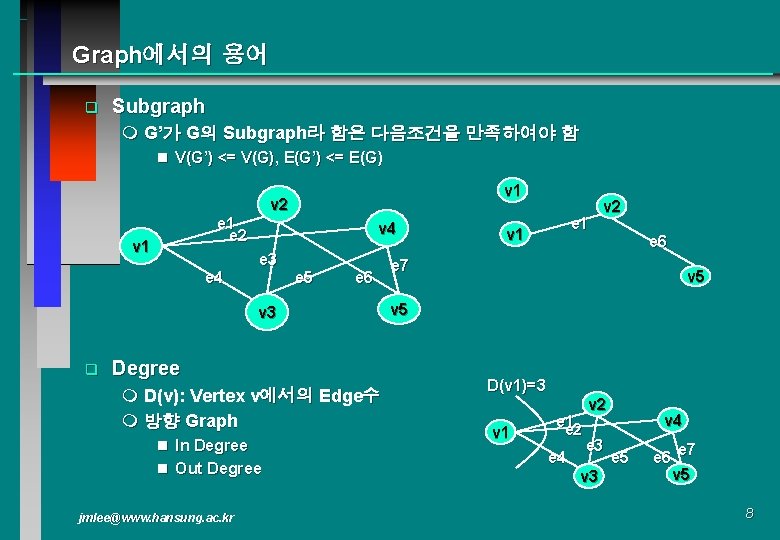
Graph에서의 용어 q Subgraph m G’가 G의 Subgraph라 함은 다음조건을 만족하여야 함 n V(G’) <= V(G), E(G’) <= E(G) v 1 v 2 e 1 e 2 v 1 e 4 v 4 e 3 e 5 e 6 v 3 q Degree m D(v): Vertex v에서의 Edge수 m 방향 Graph n In Degree n Out Degree jmlee@www. hansung. ac. kr e 1 v 2 e 6 e 7 v 5 D(v 1)=3 v 1 e 2 e 4 v 2 e 3 v 4 e 5 e 6 e 7 v 5 8

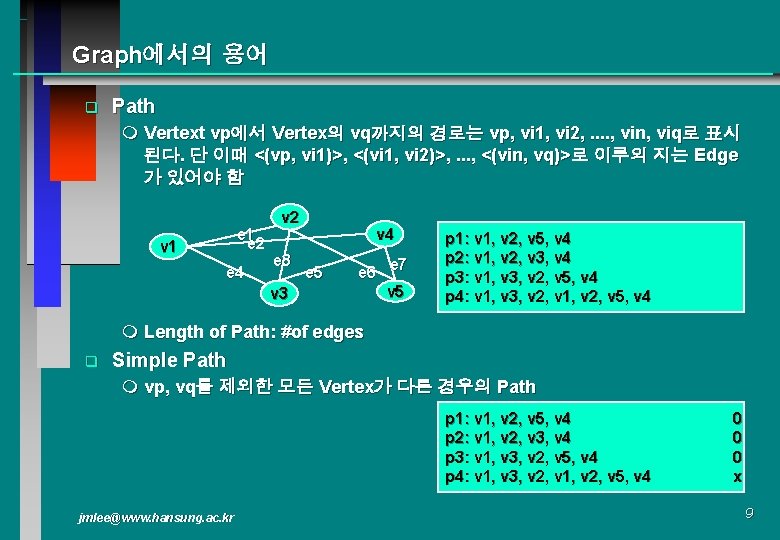
Graph에서의 용어 q Path m Vertext vp에서 Vertex의 vq까지의 경로는 vp, vi 1, vi 2, . . , vin, viq로 표시 된다. 단 이때 <(vp, vi 1)>, <(vi 1, vi 2)>, . . . , <(vin, vq)>로 이루의 지는 Edge 가 있어야 함 e 1 e 2 v 1 e 4 v 2 e 3 v 4 e 5 e 7 e 6 v 5 p 1: v 1, v 2, v 5, v 4 p 2: v 1, v 2, v 3, v 4 p 3: v 1, v 3, v 2, v 5, v 4 p 4: v 1, v 3, v 2, v 1, v 2, v 5, v 4 m Length of Path: #of edges q Simple Path m vp, vq를 제외한 모든 Vertex가 다른 경우의 Path p 1: v 1, v 2, v 5, v 4 p 2: v 1, v 2, v 3, v 4 p 3: v 1, v 3, v 2, v 5, v 4 p 4: v 1, v 3, v 2, v 1, v 2, v 5, v 4 jmlee@www. hansung. ac. kr 0 0 0 x 9

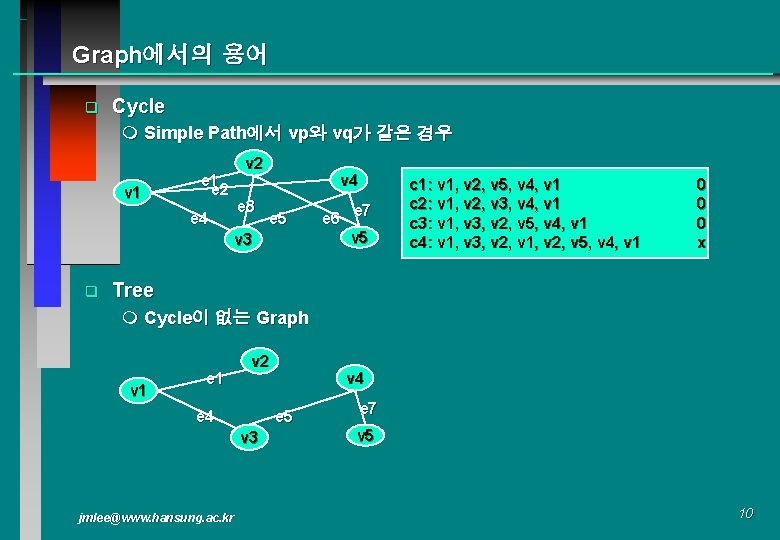
Graph에서의 용어 q Cycle m Simple Path에서 vp와 vq가 같은 경우 v 1 e 2 e 4 v 2 e 3 v 4 e 5 v 3 q e 7 e 6 v 5 c 1: v 1, v 2, v 5, v 4, v 1 c 2: v 1, v 2, v 3, v 4, v 1 c 3: v 1, v 3, v 2, v 5, v 4, v 1 c 4: v 1, v 3, v 2, v 1, v 2, v 5, v 4, v 1 0 0 0 x Tree m Cycle이 없는 Graph v 1 e 1 v 2 e 4 e 5 v 3 jmlee@www. hansung. ac. kr v 4 e 7 v 5 10

Graph의 ADT q q objects: 공집합이 아닌 Vertex의 집합과 두개의 정점을 연결하는 edge 의 집합 functions m Graph Insert. Vertex(graph, v) m Graph Insert. Edge(graph, v 1, v 2); m Graph Delete. Vertex(grapg, v) m Graph Delete. Edge(graph, v 1, v 2) m void DFS(grahp) m void BFS(graph) m void Connected(graph) m void SPT(graph) m …. jmlee@www. hansung. ac. kr 11

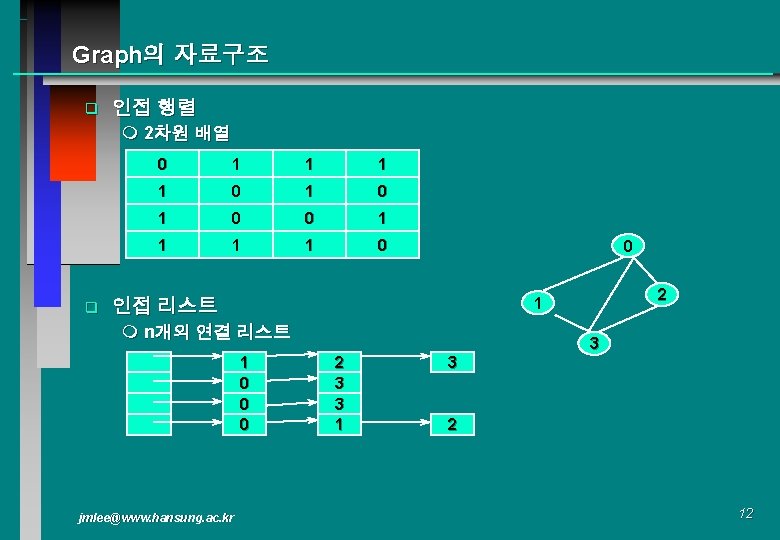
Graph의 자료구조 q 인접 행렬 m 2차원 배열 q 0 1 1 0 1 0 0 1 1 0 0 m n개의 연결 리스트 1 0 0 0 jmlee@www. hansung. ac. kr 2 1 인접 리스트 3 2 3 3 1 3 2 12

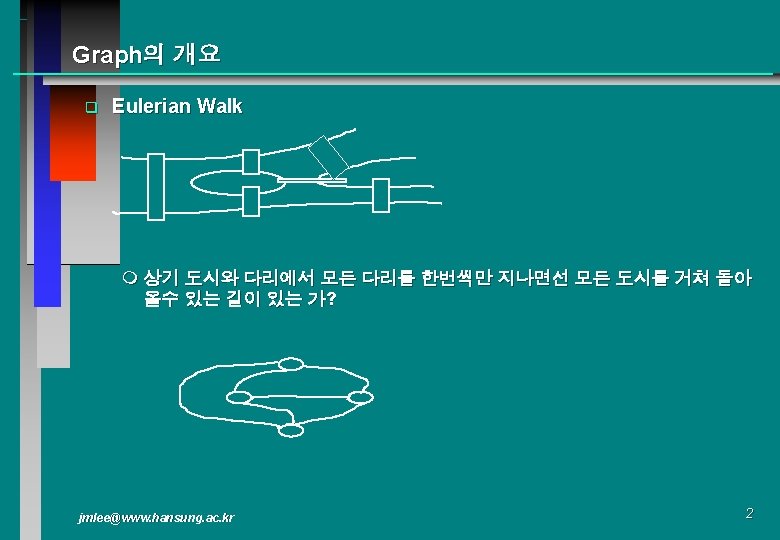
Graph의 자료구조 q C에서의 표현 int G[MAX_VERTEX]; typedef struct node_t{ int vertex; struct node_t *link; }node_t; node_t *G[MAX_VERTEX]; jmlee@www. hansung. ac. kr 13

q q q q q //MAX_VERTEX를 사용하지 않으면 typedef struct node_t{ int vertex; double ew; //가중치가 있는 경우 struct node_t *link; }node_t; typedef struct graph_t{ int vertices; node_t **nodes; }graph_t; jmlee@www. hansung. ac. kr 14

Basic Functions q 깊이 우선 탐색(Depth First Search) m그래프내의 모든 vertex을 탐색하되 인접 노드를 먼저 방문 mex) 0 0 4 3 1 4 2 4 2 jmlee@www. hansung. ac. kr 4 2 0 3 1 4 2 0 3 3 1 0 1 4 0 3 1 2 0 0 0 2 0 3 1 4 2 3 1 2 4 2 15

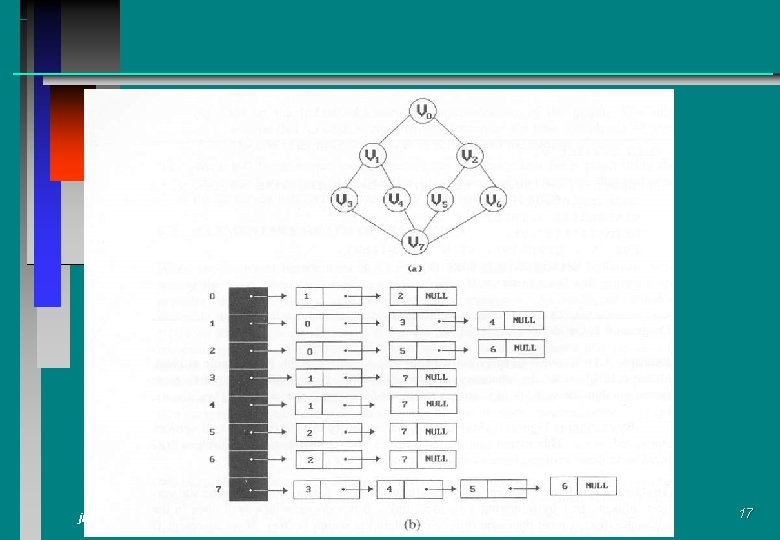
q 깊이 우선 탐색 (Depth First Search) m그래프내의 모든 vertex를 탐색하되 인접노드를 먼저 방문함 m Preorder tree traversal m. Ex) v 0, v 1, v 3, v 7, v 4, v 5, v 2, v 6 q 너비 우선 탐색 (Breadth First Search) m. Level order tree traversal m. Ex) v 0, v 1, v 2, v 3, v 4, v 5, v 6, v 7 jmlee@www. hansung. ac. kr 16

jmlee@www. hansung. ac. kr 17

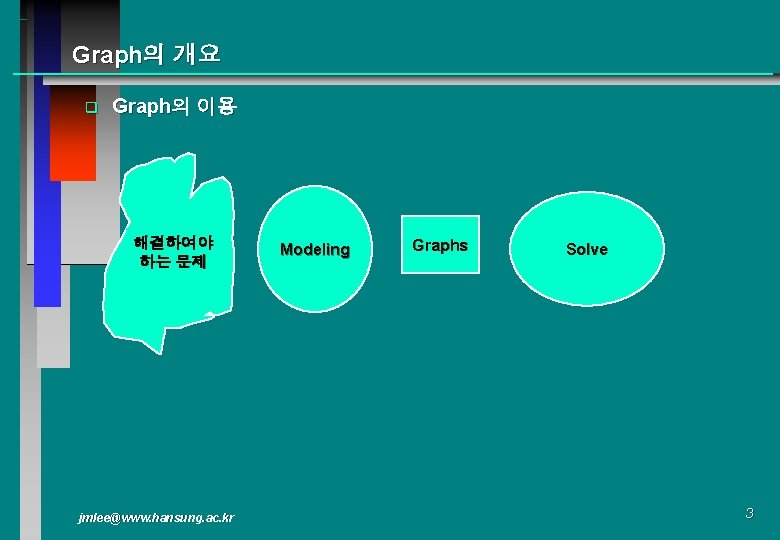
Basic Functions q dfs의 구현 int visited[MAX_VERTEX]; main() { node_t *G[MAX_VERTEX]; …. . For(I=0; I<MAX_VERTEX; I++) visited[I]= 0; dfs(G, 0); } void dfs(node_t *G[], int v) { node_t *w; visited[v]=1; printf(“%d “, v); for(w= G[v]; w!=NULL; w=w->link) if(visited[w->vertex]==0) dfs(G, w->vertex); } jmlee@www. hansung. ac. kr 18

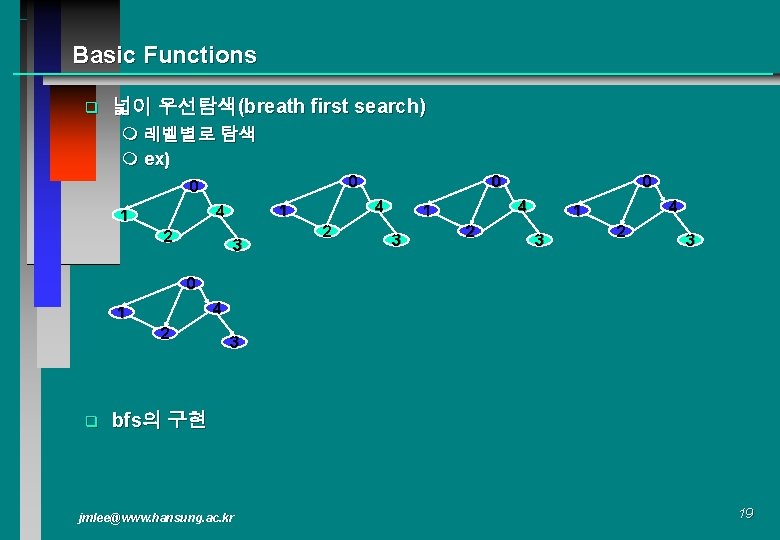
Basic Functions q 넓이 우선탐색(breath first search) m 레벨별로 탐색 m ex) 0 0 2 4 1 3 2 3 0 4 1 2 q 3 bfs의 구현 jmlee@www. hansung. ac. kr 19

void addq(queue_pointer *, int); int deleteq(queue_pointer *); BFS의 구현 void bfs(int v) { node_pointer w; queue_pointer front, rear; typedef struct queue { front = rear = NULL; int vertex; printf(“%5 d”, v); struct queue *link; visited[v] = TRUE; }queue; addq(&front, &rear, v); typedef struct queue *queue_pointer; while (front) { v =deleteq(&front); for (w = graph[v]; w; w = w->link) if (!visited[w->vertex]) { printf(“%5 d”, w->vertex); addq(&front, &rear, w->vertex); visited[w->vertex] = TRUE; } } q jmlee@www. hansung. ac. kr 20

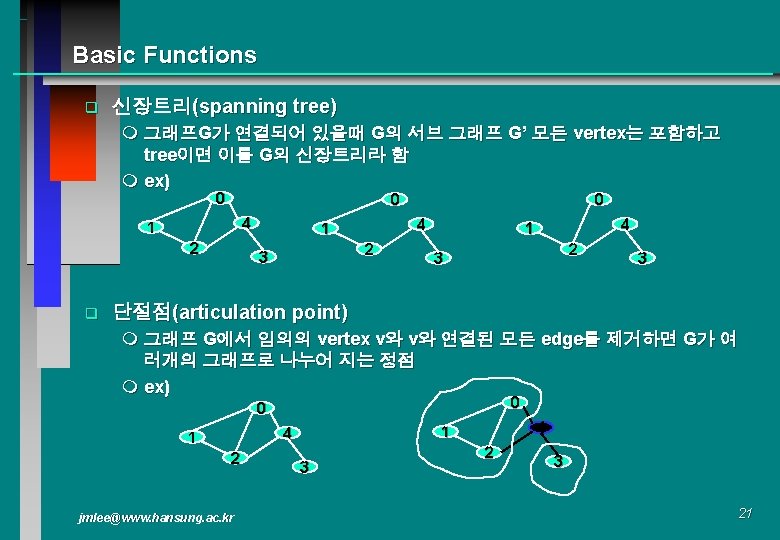
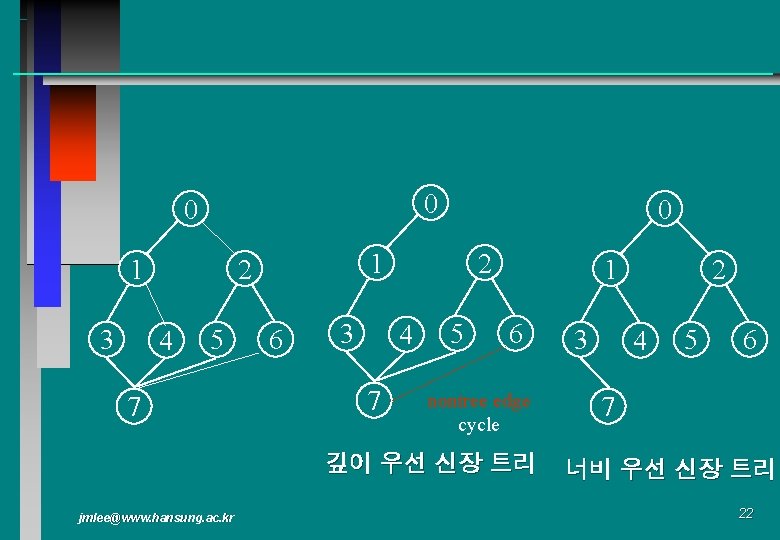
0 0 1 3 1 2 4 5 7 0 6 3 2 4 7 5 1 6 nontree edge cycle 깊이 우선 신장 트리 jmlee@www. hansung. ac. kr 3 2 4 5 6 7 너비 우선 신장 트리 22

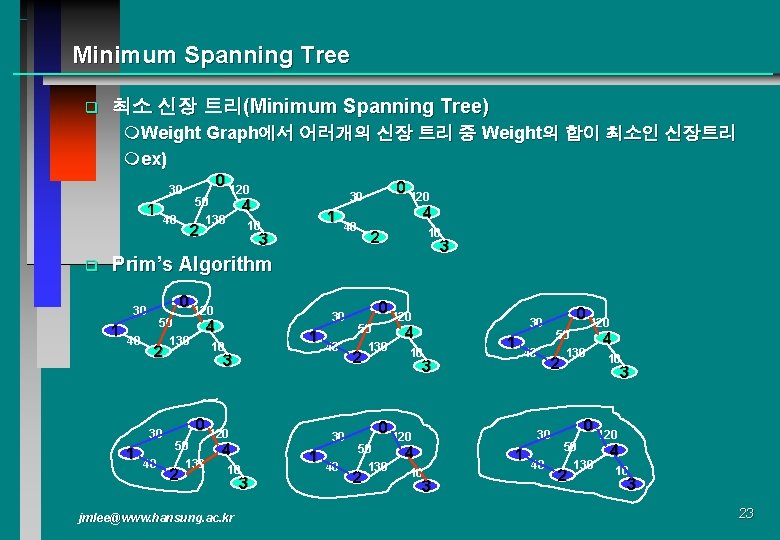
Minimum Spanning Tree q 최소 신장 트리(Minimum Spanning Tree) m. Weight Graph에서 어러개의 신장 트리 중 Weight의 합이 최소인 신장트리 mex) 30 1 q 40 0 120 50 130 4 1 10 2 0 120 30 3 40 4 10 2 3 Prim’s Algorithm 0 120 30 1 40 50 130 1 4 40 1 10 2 30 30 3 0 120 50 130 2 30 4 10 jmlee@www. hansung. ac. kr 40 3 1 40 0 120 50 130 2 4 10 3 1 40 0 120 50 130 2 0 120 30 2 30 4 1 10 3 50 130 40 4 10 3 0 120 50 130 2 4 10 3 23

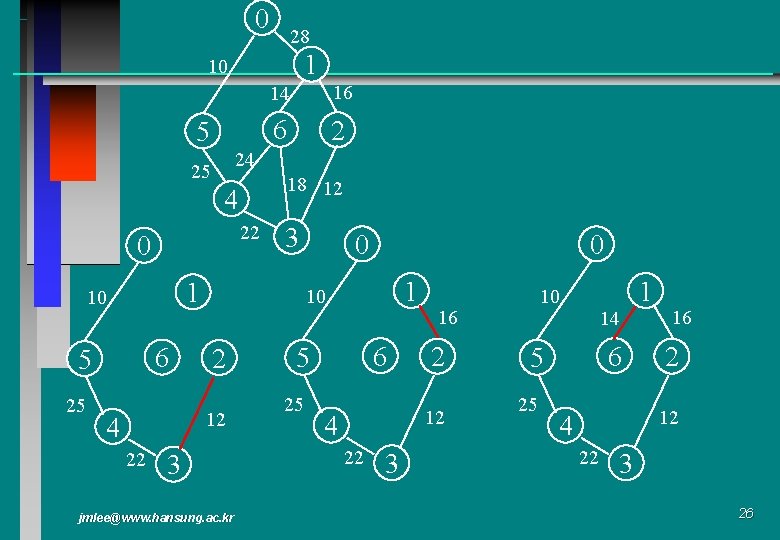
Examples for Prim’s Algorithm 0 28 1 10 14 6 5 25 0 6 5 18 12 22 1 2 2 24 4 10 16 3 0 0 10 6 5 4 3 jmlee@www. hansung. ac. kr 2 4 3 6 5 25 25 1 10 1 2 4 22 3 25

0 28 1 10 5 16 6 2 24 25 18 12 4 22 0 3 1 10 6 5 25 14 22 0 1 10 2 12 4 0 3 jmlee@www. hansung. ac. kr 6 5 25 16 2 12 4 22 3 1 10 14 6 5 25 16 2 12 4 22 3 26

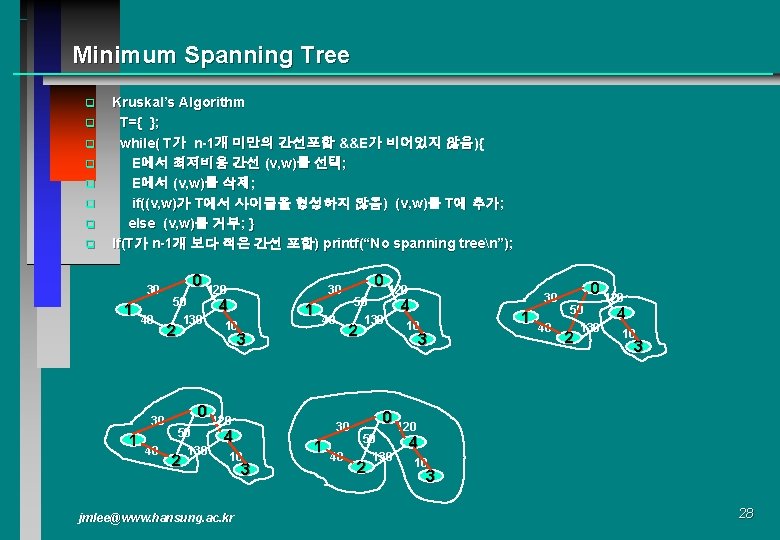
Minimum Spanning Tree q q q q Kruskal’s Algorithm T={ }; while( T가 n-1개 미만의 간선포함 &&E가 비어있지 않음){ E에서 최저비용 간선 (v, w)를 선택; E에서 (v, w)를 삭제; if((v, w)가 T에서 사이클을 형성하지 않음) (v, w)를 T에 추가; else (v, w)를 거부; } If(T가 n-1개 보다 적은 간선 포함) printf(“No spanning treen”); 30 1 40 0 120 50 130 2 4 1 10 40 0 120 2 30 4 10 jmlee@www. hansung. ac. kr 3 1 50 130 2 3 50 130 0 120 30 4 1 10 3 40 0 120 50 130 2 4 10 3 28

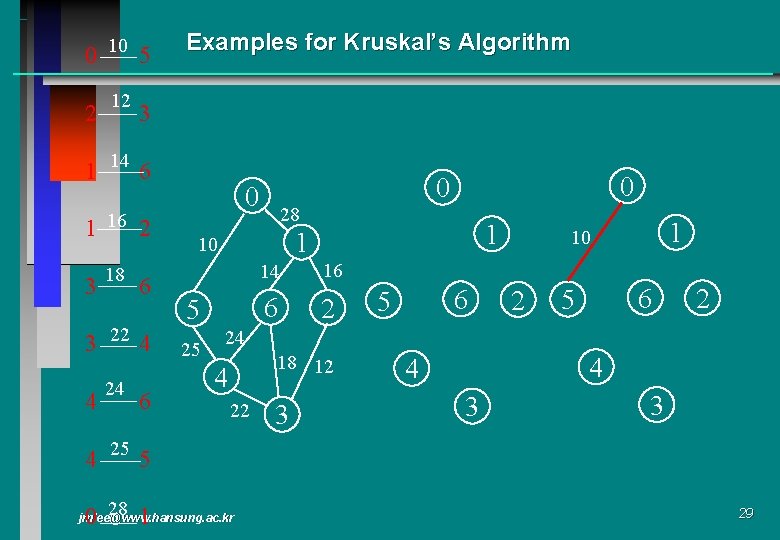
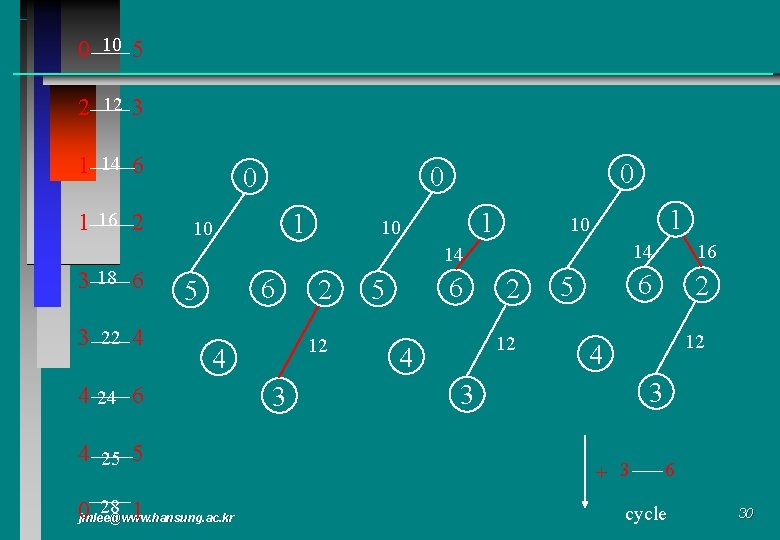
0 10 5 2 12 Examples for Kruskal’s Algorithm 3 1 14 6 1 16 3 18 2 6 3 22 4 4 24 6 0 28 1 1 10 5 25 0 0 14 16 6 2 6 5 1 10 2 6 5 2 24 18 12 4 22 3 4 4 3 3 4 25 5 0 28 1 jmlee@www. hansung. ac. kr 29

0 10 5 2 12 3 1 14 6 1 16 2 0 0 0 1 10 14 3 18 6 3 22 4 6 5 12 4 4 24 6 4 25 5 28 1 0 jmlee@www. hansung. ac. kr 2 3 6 5 2 12 4 5 14 16 6 2 12 4 3 3 + 3 6 cycle 30

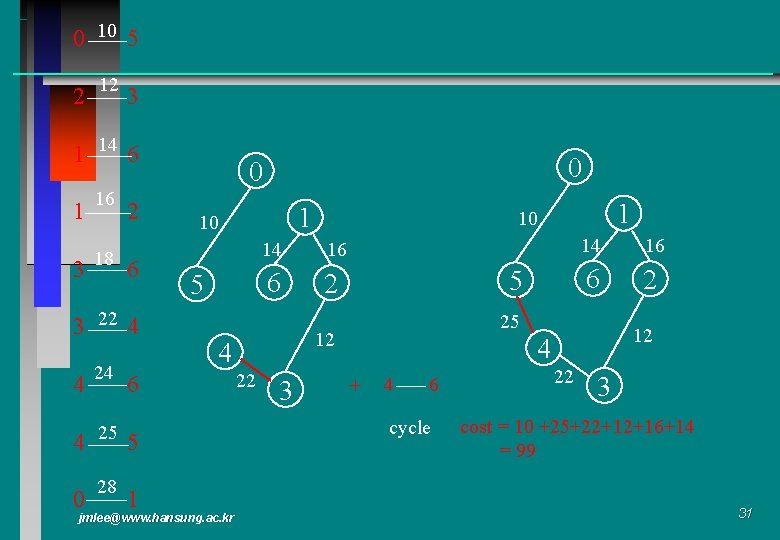
0 10 5 2 12 3 1 14 6 1 16 2 3 18 6 3 22 4 4 25 0 28 1 10 5 16 6 2 5 jmlee@www. hansung. ac. kr 5 3 14 16 6 2 25 12 22 1 10 14 4 6 1 0 0 12 4 + 4 6 cycle 22 3 cost = 10 +25+22+12+16+14 = 99 31

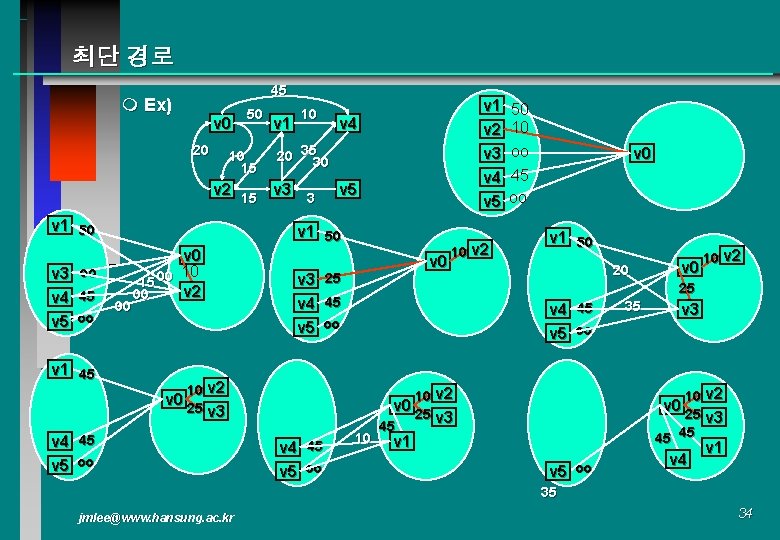
최단 경로 45 m Ex) v 0 20 50 10 15 v 1 10 v 3 oo v 4 45 v 5 oo v 1 45 v 4 20 3530 v 2 v 3 15 3 v 1 50 v 2 10 v 3 oo v 4 45 v 5 oo v 5 v 1 50 00 v 0 10 15 00 v 2 00 v 3 25 v 4 45 v 5 oo v 1 50 20 v 4 45 v 5 oo 10 v 2 25 v 3 10 v 2 10 45 35 v 3 10 v 2 25 v 3 45 45 v 0 25 v 4 45 v 5 oo 10 v 2 v 0 25 v 1 v 5 oo v 4 v 1 35 jmlee@www. hansung. ac. kr 34

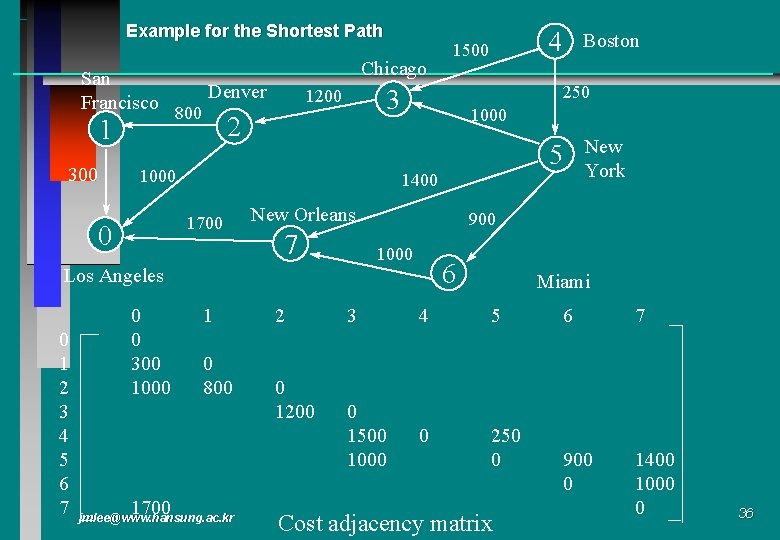
Example for the Shortest Path San Francisco 1 300 Chicago Denver 800 2 1000 0 1000 New Orleans 7 0 1 2 3 4 5 6 7 1700 1 0 800 jmlee@www. hansung. ac. kr 2 0 1200 New York 900 1000 6 Los Angeles 0 0 300 1000 5 1400 1700 Boston 250 3 1200 4 1500 Miami 3 4 5 0 1500 1000 0 250 0 Cost adjacency matrix 6 7 900 0 1400 1000 0 36

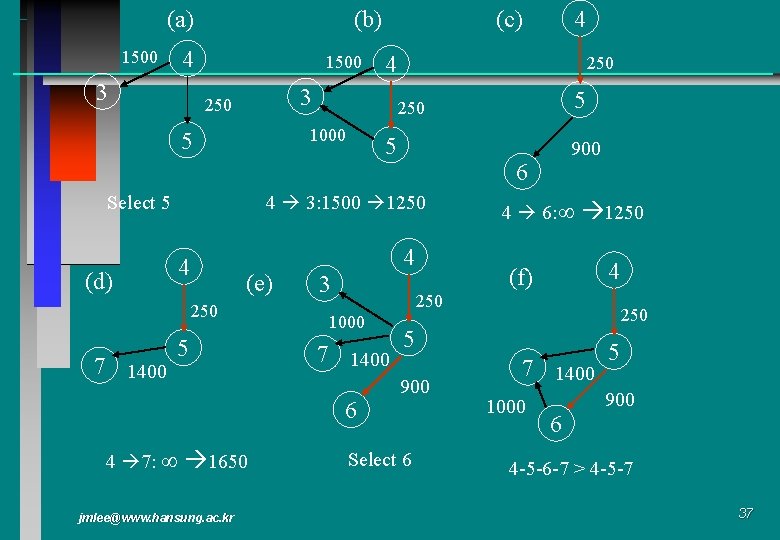
(a) (b) 4 1500 3 1500 5 4 (e) 5 4 3 1650 jmlee@www. hansung. ac. kr 900 4 6: 1250 4 (f) 250 1000 7 1400 6 4 7: 5 6 4 3: 1500 1250 7 1400 250 1000 Select 5 4 4 3 250 5 (d) (c) 250 5 900 Select 6 7 1400 1000 6 5 900 4 -5 -6 -7 > 4 -5 -7 37

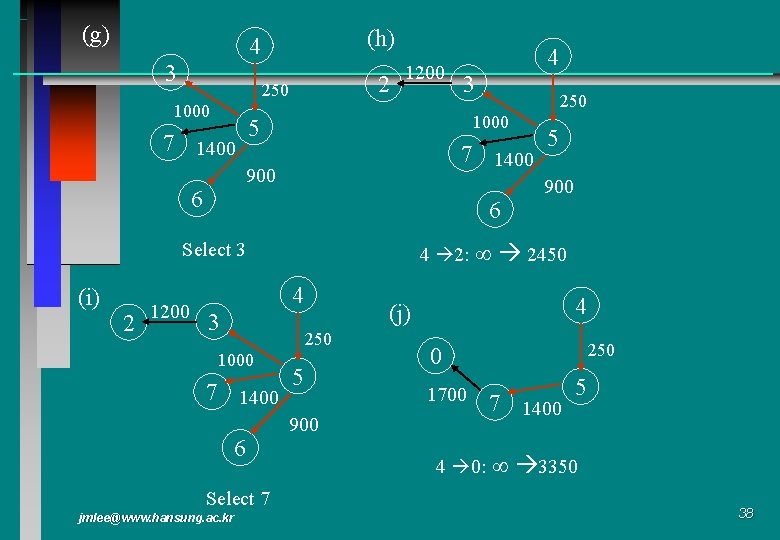
(g) (h) 4 3 2 250 1000 1200 6 4 2: Select 3 (i) 2 1200 250 7 1400 900 6 3 1000 5 7 1400 4 4 3 7 1400 6 Select 7 jmlee@www. hansung. ac. kr 900 2450 4 (j) 250 1000 5 5 900 250 0 1700 7 1400 4 0: 5 3350 38

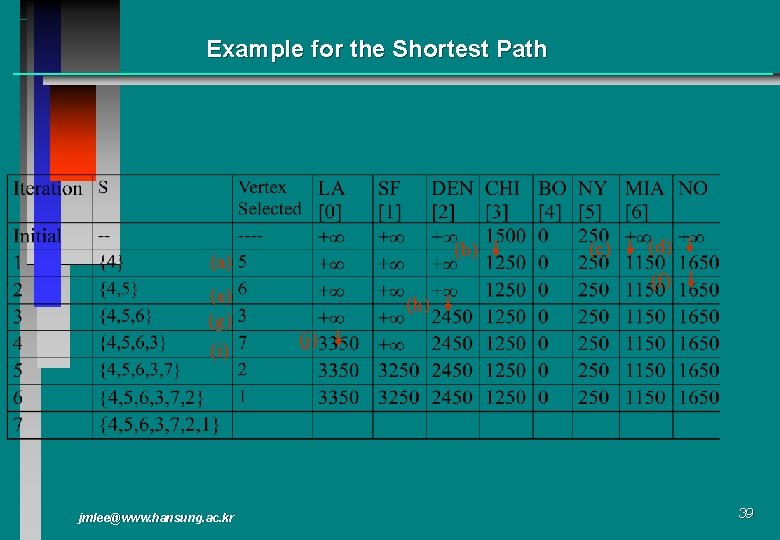
Example for the Shortest Path (b) (a) (e) (g) (i) jmlee@www. hansung. ac. kr (c) (d) (f) (h) (j) 39

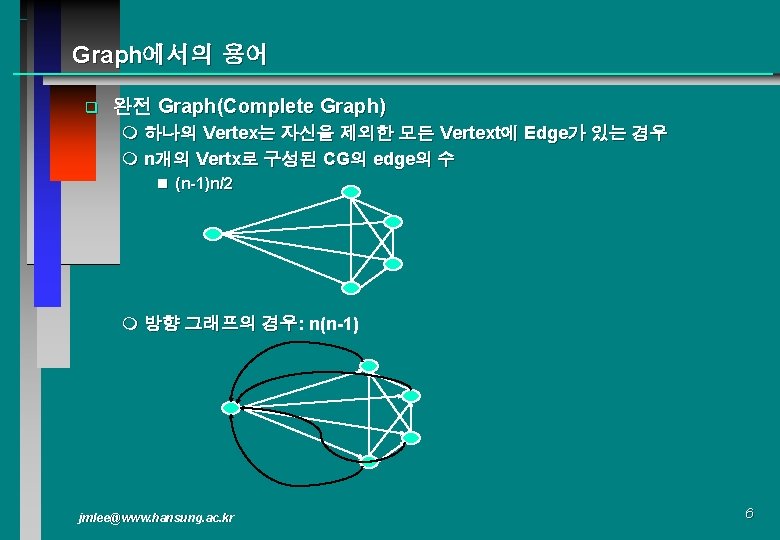
최단 경로와 이행적 폐쇄 (3) #define MAX_VERTICES 6 int cost[][MAX_VERTICES] = { {0, 50, 1000, 45, 1000}, {1000, 0, 15, 1000, 1000}, {20, 1000, 0, 15, 1000}, {1000, 20, 1000, 0, 35, 1000}, {1000, 30, 1000, 0, 1000}, {1000, 3, 1000, 0} }; int distance[MAX_VERTICES]; short int found[MAX_VERTICES]; int n = MAX_VERTICES; void shortestpath(int v, int cost[][MAX_VERTICES, int distance[], int n, short int found[]) { int i, u, w; for (i=0; I < n; I++) { found[i] = FALSE; distance[i] = cost[v][i]; } found[v] = TRUE; distance[v] = 0; for (i=0; i < n-2; I++) { u = choose(distance, n, found); found[u] = TRUE; for (w=0; w<n; w++) if (!found[w]) if (distance[u] + cost[u][w] < distance[w]) distance[w] = distance[u] + cost[u][w]; } } jmlee@www. hansung. ac. kr 40

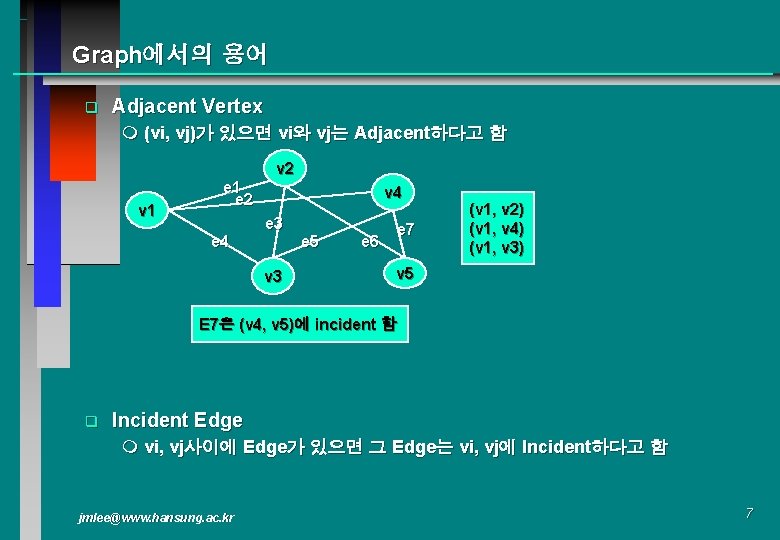
int choose(int distance[], int n, short int found[]) { int i, minpos; min = INT_MAX; minpos = -1; for (i=0; i < n; i++) if (distance[I] < min && !found[I]) { min = distance[I]; minpos = i; } return minpos } jmlee@www. hansung. ac. kr 41

A 0 A-1 6 V 0 3 11 4 V 1 2 V 2 A 1 jmlee@www. hansung. ac. kr A 2 43

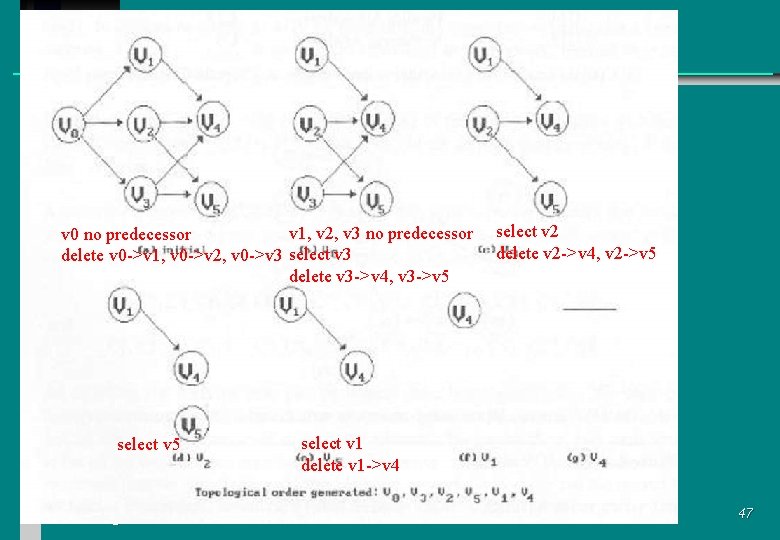
Two topological orders C 1, C 2, C 4, C 5, C 3, C 6, C 8, C 7, C 10, C 13, C 12, C 14, C 15, C 11, C 9 C 4, C 5, C 2, C 1, C 6, C 3, C 8, C 15, C 7, C 9, C 10, C 11, C 13, C 12, C 14 jmlee@www. hansung. ac. kr 45

v 1, v 2, v 3 no predecessor v 0 no predecessor delete v 0 ->v 1, v 0 ->v 2, v 0 ->v 3 select v 3 delete v 3 ->v 4, v 3 ->v 5 select v 5 jmlee@www. hansung. ac. kr select v 2 delete v 2 ->v 4, v 2 ->v 5 select v 1 delete v 1 ->v 4 47

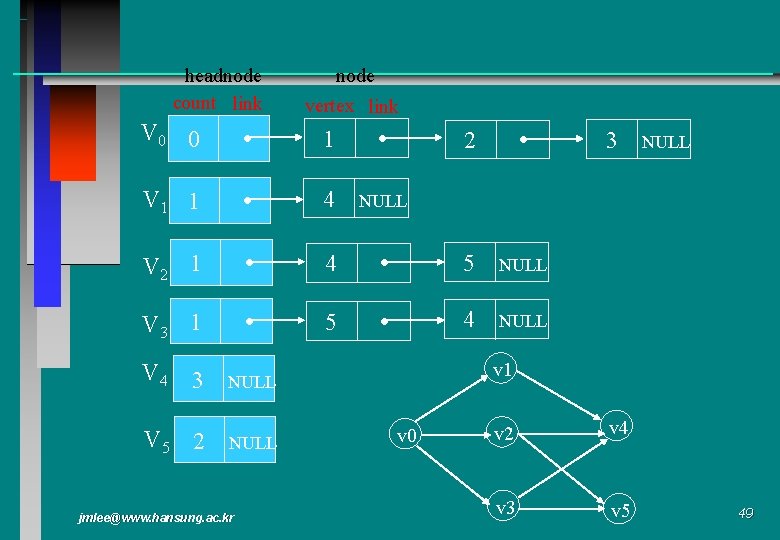
headnode count link node vertex link V 0 0 1 V 1 1 4 NULL V 2 1 4 V 3 1 5 V 4 3 V 5 2 2 5 NULL 4 NULL jmlee@www. hansung. ac. kr NULL v 1 NULL 3 v 0 v 2 v 4 v 3 v 5 49

void topsort(hdnodes graph[], int n) { int i, j, k, top; node_pointer ptr; // 선행자를 갖지 않는 정점들의 스택 생성 top = -1; for (i=0; i < n; i++) { if (!graph[i]. count) { graph[i]. count = top; top = i; } } for (i=0; i < n; i++) if (top == -1) { fprintf(stderr, “n. Network has a cycle. Sort terminated. n”); exit(1); } else { j = top; // 정점을 스택에서 꺼냄 top = graph[top]. count; printf(“v%d, “, j); for (ptr = graph[j]. link; ptr = ptr->link) { k = ptr ->vertex; graph[k]. count--; // j의 후속자 정점 수 감소 if (!graph[k]. count) { graph[k]. count = top; // add vertex k to the stack top = k; jmlee@www. hansung. ac. kr } 50