Graph Outline Introduction to graph Is there a

Graph

Outline • • Introduction to graph Is there a Eulerian trail, curcuit? Isomorphism and planarity Shortest path problem

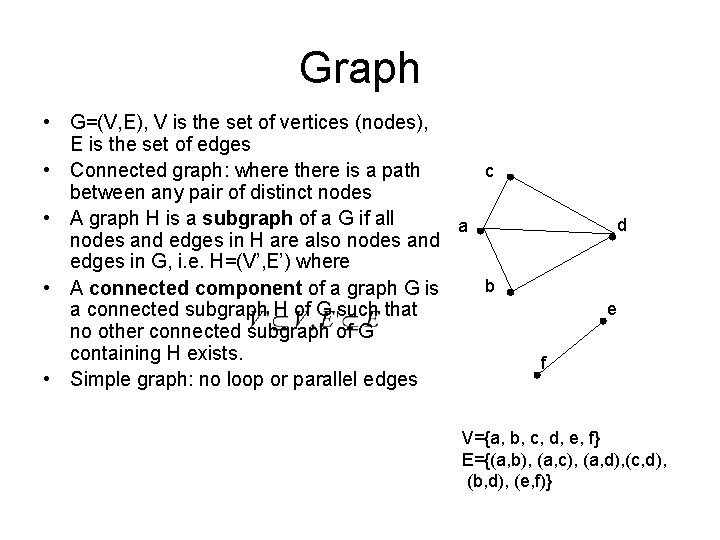
Graph • G=(V, E), V is the set of vertices (nodes), E is the set of edges • Connected graph: where there is a path c between any pair of distinct nodes • A graph H is a subgraph of a G if all a nodes and edges in H are also nodes and edges in G, i. e. H=(V’, E’) where b • A connected component of a graph G is a connected subgraph H of G such that no other connected subgraph of G containing H exists. • Simple graph: no loop or parallel edges d e f V={a, b, c, d, e, f} E={(a, b), (a, c), (a, d), (c, d), (b, d), (e, f)}

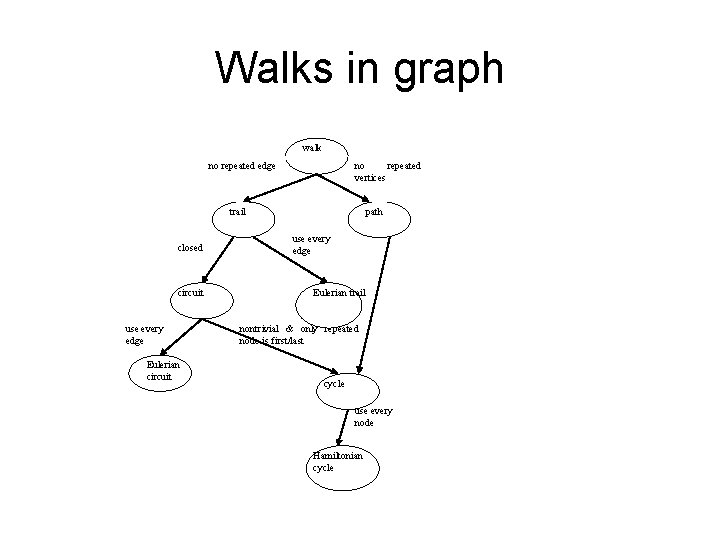
Walks in graph walk no repeated edge no repeated vertices trail closed circuit use every edge Eulerian circuit path use every edge Eulerian trail nontrivial & only repeated node is first/last cycle use every node Hamiltonian cycle

Does a graph has an Eulerian trail ? C D A B • A Walk that go through all edges exactly once • Proposition: in any graph, if a vertex x has an odd degree, then x cannot be an interior vertex (i. e. , a vertex other than the starting or stopping point) in an Eulerian trail. – For interior vertex: vs…e 1 xe 2 … e 3 xe 4 … ve

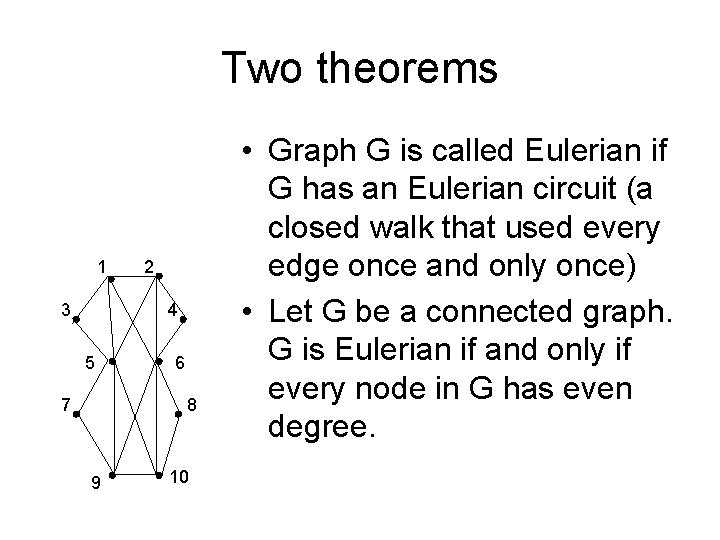
Two theorems 1 3 2 4 5 7 6 8 9 10 • Graph G is called Eulerian if G has an Eulerian circuit (a closed walk that used every edge once and only once) • Let G be a connected graph. G is Eulerian if and only if every node in G has even degree.

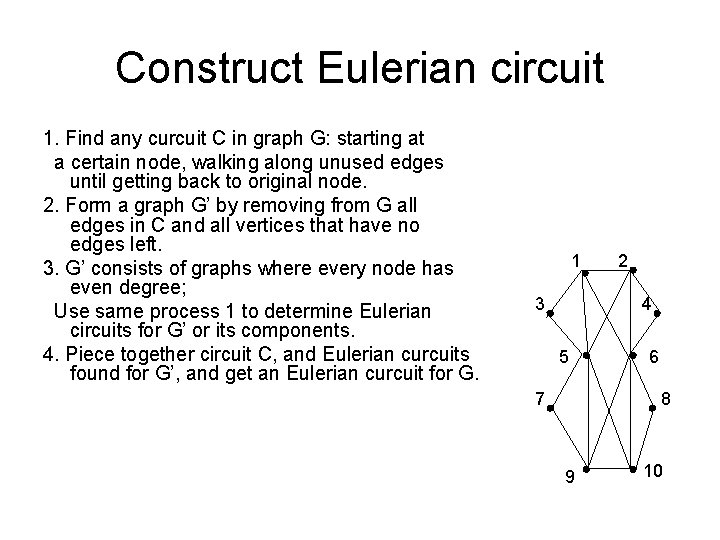
Construct Eulerian circuit 1. Find any curcuit C in graph G: starting at a certain node, walking along unused edges until getting back to original node. 2. Form a graph G’ by removing from G all edges in C and all vertices that have no edges left. 3. G’ consists of graphs where every node has even degree; Use same process 1 to determine Eulerian circuits for G’ or its components. 4. Piece together circuit C, and Eulerian curcuits found for G’, and get an Eulerian curcuit for G. 1 3 2 4 5 7 6 8 9 10

Eulerian Trail • A connected graph G has an Eulerian trail if and only if G has exactly two nodes of odd degree. Moveover, the trail must begin and end at these two nodes – If G has exactly two nodes of odd degree, after adding an edge connecting these two nodes, G has Eulerian circuit (by previous theorem). By removing added edge from circuit, we get a trail starting/ending at two nodes. – If G has an Eulerian trail, it’s easy to see that the starting/ending nodes have odd degree, all other nodes have even degree.

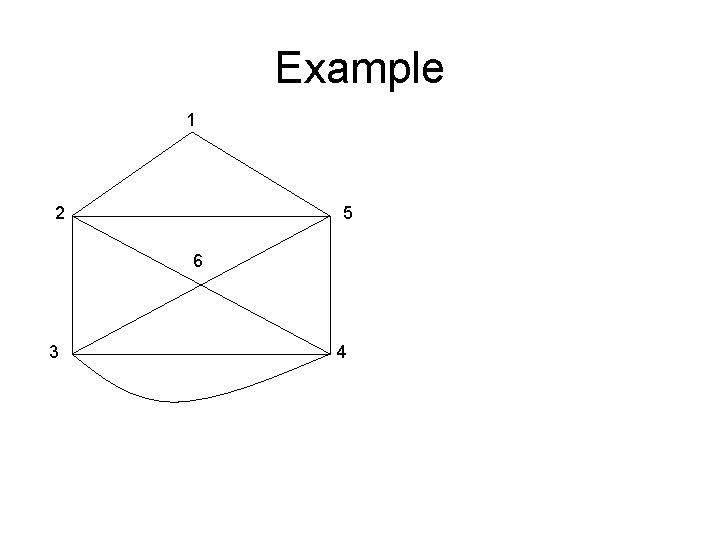
Example 1 2 5 6 3 4

Outline • • Introduction to graph Is there a Eulerian trail, curcuit? Isomorphism and planarity Shortest path problem

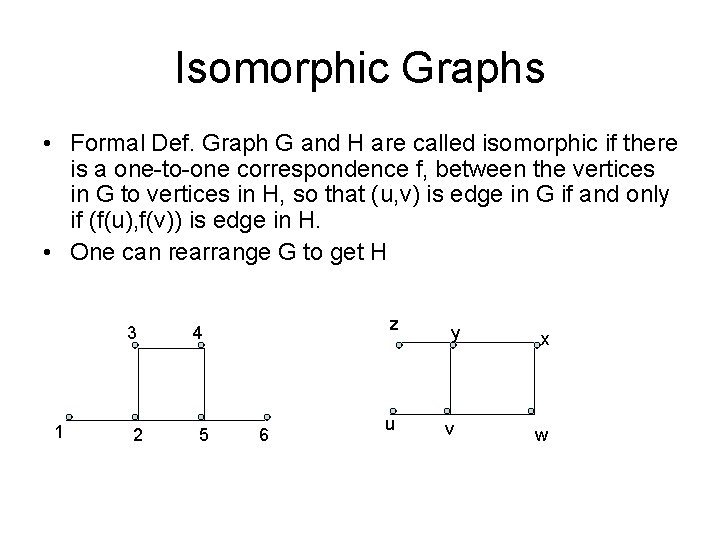
Isomorphic Graphs • Formal Def. Graph G and H are called isomorphic if there is a one-to-one correspondence f, between the vertices in G to vertices in H, so that (u, v) is edge in G if and only if (f(u), f(v)) is edge in H. • One can rearrange G to get H 3 1 2 z 4 5 6 u y v x w

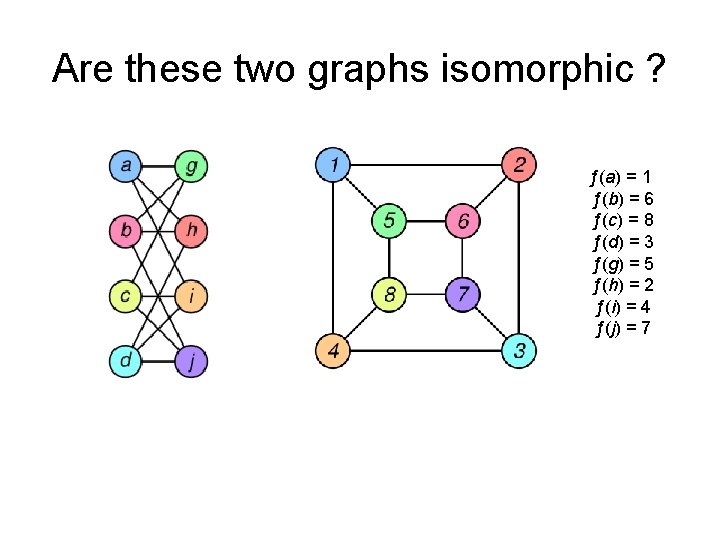
Are these two graphs isomorphic ? ƒ(a) = 1 ƒ(b) = 6 ƒ(c) = 8 ƒ(d) = 3 ƒ(g) = 5 ƒ(h) = 2 ƒ(i) = 4 ƒ(j) = 7

Checking isomorphism • Two graphs that are isomorphic to one another must have – – – Same number of nodes Same number of edges Same number of nodes of any given degree Same number of cycles of any given size • A pair of graphs satisfying above conditions are not necessarily isomorphic

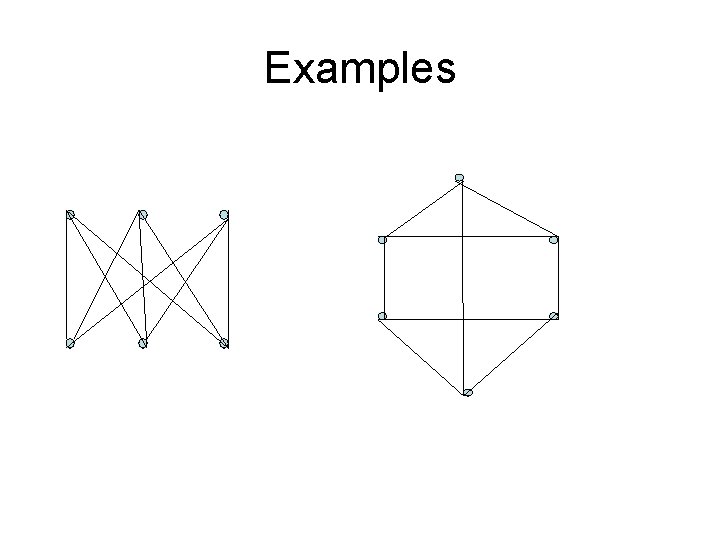
Examples

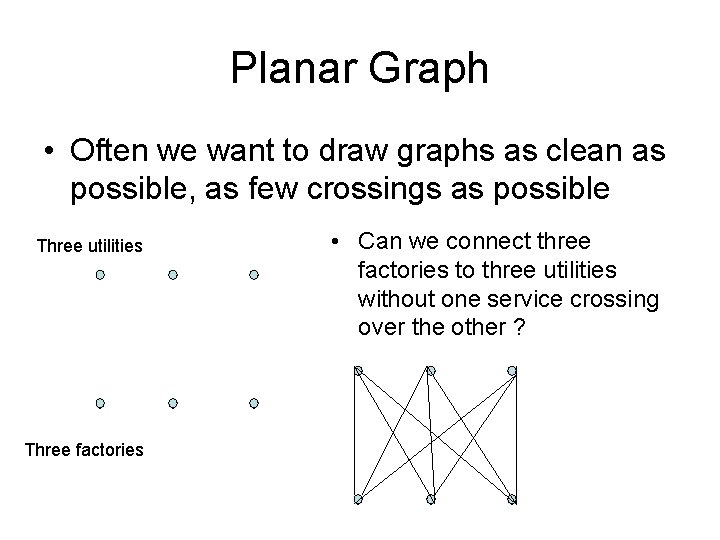
Planar Graph • Often we want to draw graphs as clean as possible, as few crossings as possible Three utilities Three factories • Can we connect three factories to three utilities without one service crossing over the other ?

Definitions • A graph is called planar if it can be drawn on a plane so that no edges cross. Such a drawing is called an embedding. • Bipartite graph: the set of nodes can be partitioned into two sets so that every edge has one endpoint in one set, one endpoint in another set. • Complete bipartite graph, Km, n, is a bipartite graph with nodes S 1={a 1, …, am} and S 2={b 1, …, bn}, and every nodes in S 1 is connecting to every node in S 2. • Complete graph, Kn

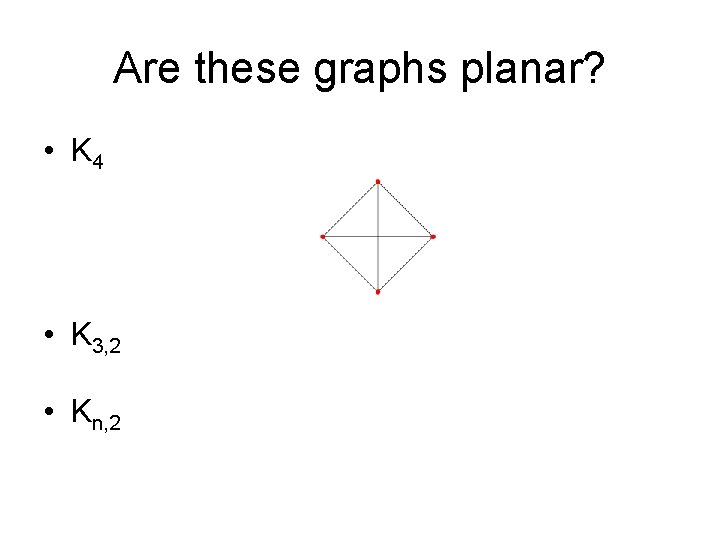
Are these graphs planar? • K 4 • K 3, 2 • Kn, 2

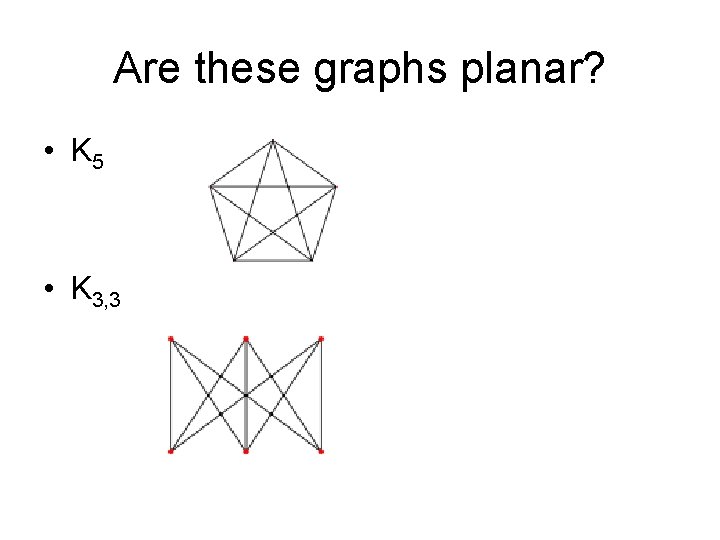
Are these graphs planar? • K 5 • K 3, 3

Kuratowski’s Theorem • A graph G is planar if and only if contains no “copies” of K 3, 3 or K 5 as subgraphs • A graph is planar if and only if it does not contain a subgraph that is a subdivision of K 5 or K 3, 3. • A subdivision of a graph results from inserting vertices into edges

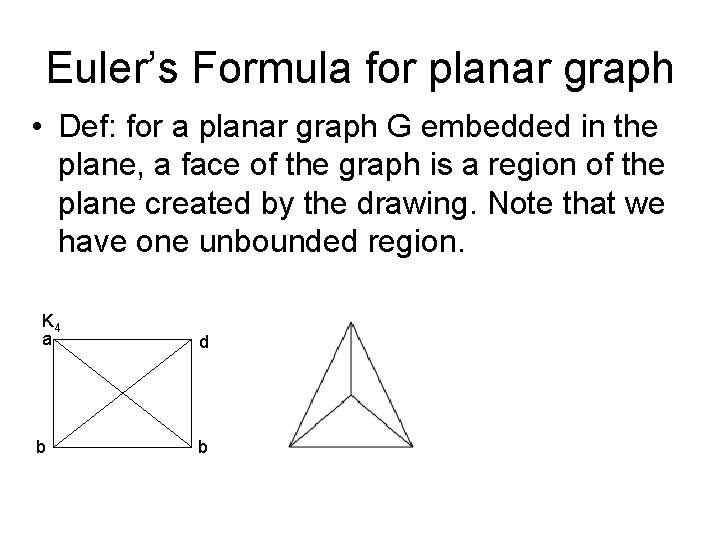
Euler’s Formula for planar graph • Def: for a planar graph G embedded in the plane, a face of the graph is a region of the plane created by the drawing. Note that we have one unbounded region. K 4 a b d b

Euler’s Formula for Planar Graph • Given an embedding of a graph, – Removing any edge from a cycle decrease by 1 the num. of faces – Every edge on a cycle borders exactly two faces – For acyclic graph, # of faces is 1 • For any connected planar graph G embedded in the plane with V vertices, E edges and F faces, it must be the case that V+F=E+2 (Euler’s formula)

Now why K 3, 3 is not planar ?

Outline • • Introduction to graph Is there a Eulerian trail, curcuit? Isomorphism and planarity Shortest path problem

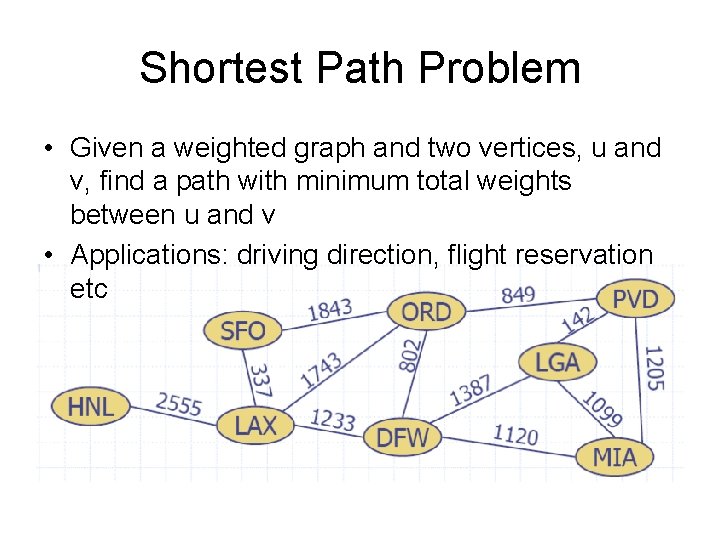
Shortest Path Problem • Given a weighted graph and two vertices, u and v, find a path with minimum total weights between u and v • Applications: driving direction, flight reservation etc

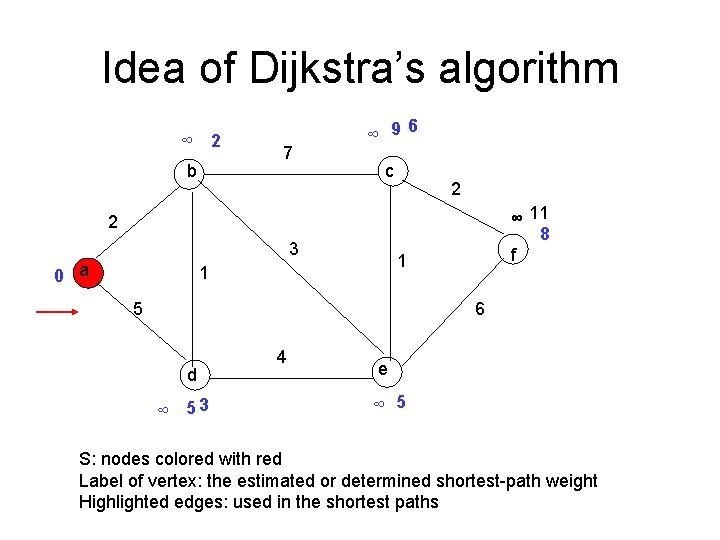
Dijkstra’s Algorithm • Find the shortest paths from a single source to all other nodes • All weights are non-negative • Ideas: – Maintain a set S of vertices whose final shortest-path weights from source have been decided – Select from V-S a vertex with minimum shortest-path estimate, insert into S – Updating shortest-path estimates for nodes in V-S – Until S=V, all nodes have been determined

Idea of Dijkstra’s algorithm ∞ 2 b 7 6 ∞ 9 c 2 ∞ 11 8 f 2 3 0 a 1 1 5 6 d ∞ 53 4 e ∞ 5 S: nodes colored with red Label of vertex: the estimated or determined shortest-path weight Highlighted edges: used in the shortest paths

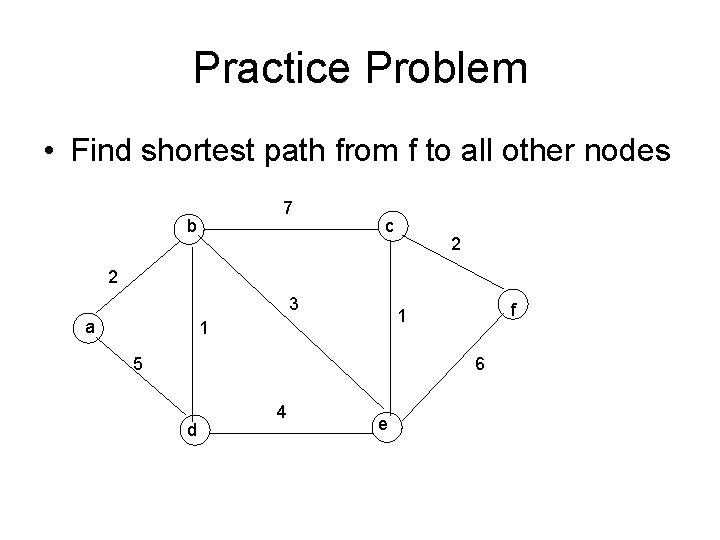
Practice Problem • Find shortest path from f to all other nodes 7 b c 2 2 3 a f 1 1 5 6 d 4 e