Introduction to Graph Theory Graph GV E Vv

Introduction to Graph Theory

Graph G=(V, E) V={v 1, v 2, …, vn} vertex=node E={(u, v)|(u, v) is an unorder pair of V} edge=link loop multiple edges

simple = no loops, no multiple edges v(G)=|V(G)| ε(G)=|E(G)| isomorphism G and H are isomorphic.

complete graph Kn adjacent matrix v☓v subgraph H ⊆ G if V(H) ⊆ V(G), E(H) ⊆ E(G) spanning subgraph V(H) = V(G) degree d. G(v) δ(G) △(G) ∑d(v)=2ε

Corollary In any graph, the number of verticesof odd degree is even. path u and v are connected if there is a (u, v)-path. component G 1, G 2, … G is connected if…

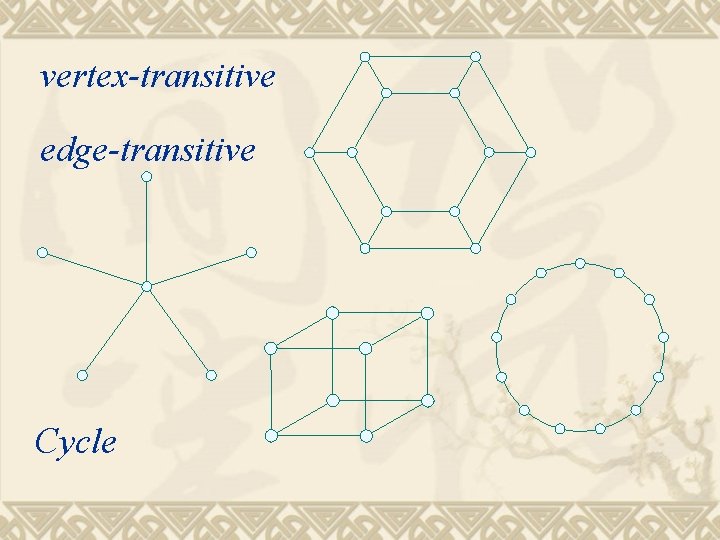
vertex-transitive edge-transitive Cycle

Theorem Bipartite iff no odd cycle. • If δ ≥ 2, then G contains a cycle. • If ε ≥ v, G contains a cycle. • If G is simple and δ ≥ 2, then G contains a cycle of length at least δ+1.

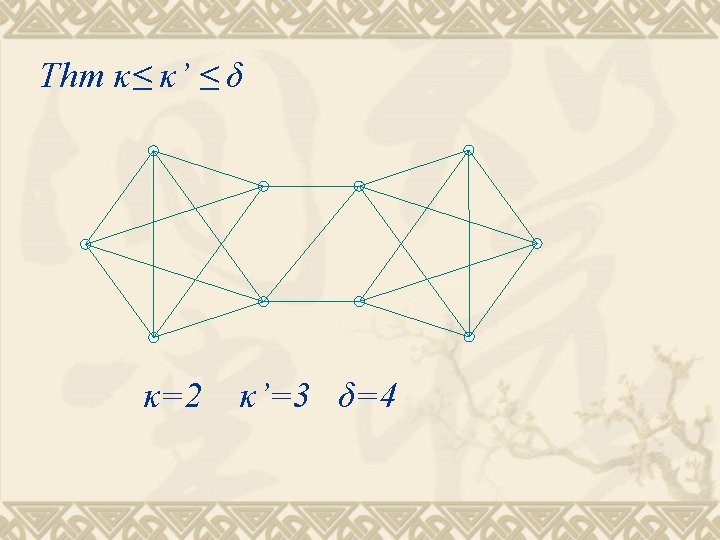
Connectivity κ(G)= minimum k for which G has a k-vertex cut G is k-connected if κ(G) ≥ k. 拿走 k點，可能斷。但 k-1點，一定不斷。

Edge-connectivity κ’(G)= minimum k for which G has a k-edge cut G is k-edge-connected if κ’(G) ≥ k. 拿走 k線，可能斷。但 k-1線，一定不斷。

Euler Tour Hamiltonian Cycle Hamiltonian Theorem If G is simple graph with v ≥ 3 and δ ≥ v/2, then G is hamiltonian

Hamiltonian connected How about bipartite graphs ? ? Hamiltonian laceable (Hamiltonian bi-connected)

fault-tolerant edge-fault-tolerant pancyclic bipancyclic pan=泛 panconnected bipanconnected

Matching Perfect matching Theorem G=(X, Y, E) contains a matching that saturates every vertex in X iff |N(S)| ≥ |S| for all S ⊆ X. Coroallary If G is k-regular bipartite graph with k > 0, then G has a perfect matching.

Edge coloring Edge chromatic number= χ’ Vizing Theorem G is simple, then χ’ = ∆ or ∆+1 But …

Vertex coloring Chromatic number= χ Coroallary For any graph G, χ ≤ ∆+1

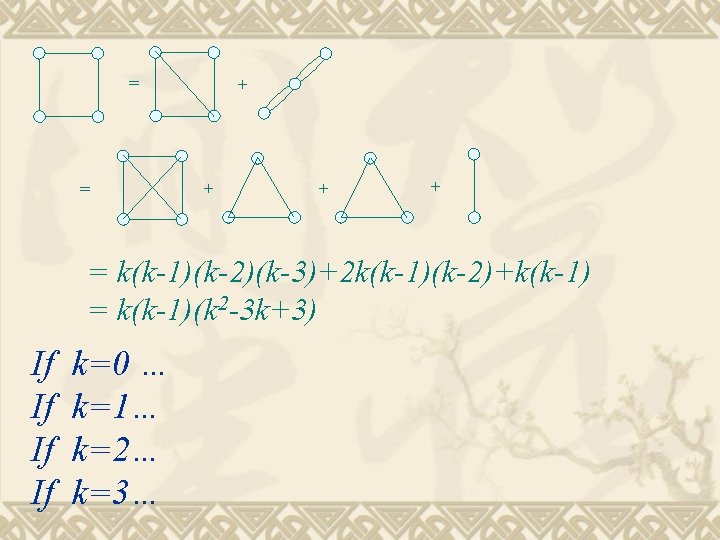
πk(G) = chromatic polynomial Theorem If G is simple, then πk(G)= πk(G-e) -πk(G∙ e) πk(G)= πk(G+e) +πk(G∙ e) e e = e +

= = + + = k(k-1)(k-2)(k-3)+2 k(k-1)(k-2)+k(k-1) = k(k-1)(k 2 -3 k+3) If If k=0 … k=1… k=2… k=3…