Introduction to Graph Theory Definition of Graph A

Introduction to Graph Theory

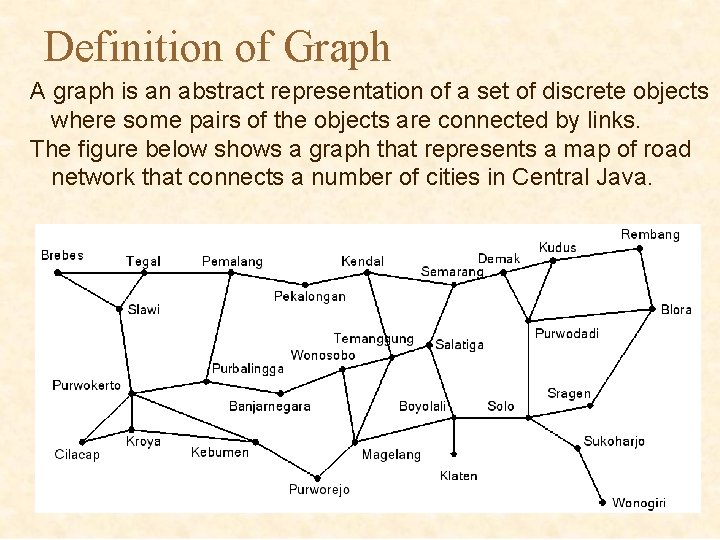
Definition of Graph A graph is an abstract representation of a set of discrete objects where some pairs of the objects are connected by links. The figure below shows a graph that represents a map of road network that connects a number of cities in Central Java.

Bridges of Königsberg (Euler, 1736) Can someone pass every bridge exactly once and come back the his/her original position? A graph can be used to represent the Königsberg bridge: Vertex represents a dry land Arc or edge represents a bridge

Graph Representation Graph G = (V, E) where: V = Set of vertices, may not be a null set = {v 1, v 2, . . . , vn} E = Set of edges, each connecting a pair of vertices = {e 1, e 2, . . . , en}

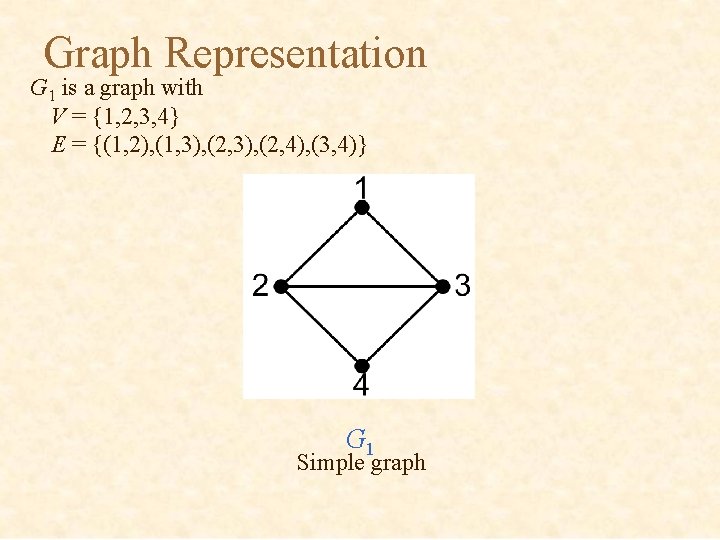
Graph Representation G 1 is a graph with V = {1, 2, 3, 4} E = {(1, 2), (1, 3), (2, 4), (3, 4)} G 1 Simple graph

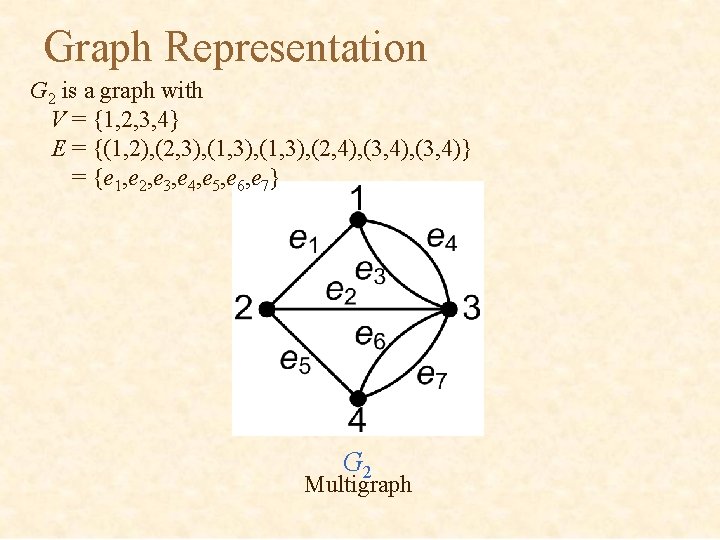
Graph Representation G 2 is a graph with V = {1, 2, 3, 4} E = {(1, 2), (2, 3), (1, 3), (2, 4), (3, 4)} = {e 1, e 2, e 3, e 4, e 5, e 6, e 7} G 2 Multigraph

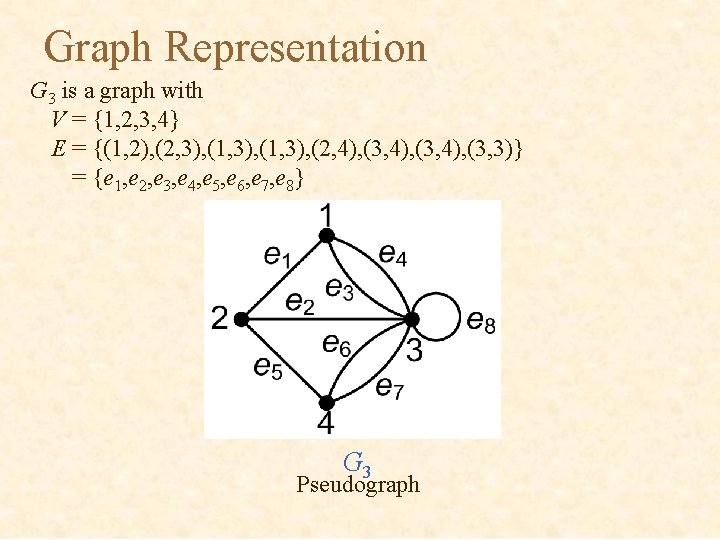
Graph Representation G 3 is a graph with V = {1, 2, 3, 4} E = {(1, 2), (2, 3), (1, 3), (2, 4), (3, 3)} = {e 1, e 2, e 3, e 4, e 5, e 6, e 7, e 8} G 3 Pseudograph

Graph Classification Based on the existence of loop or multiple edges, a graph can be classified into: 1. Simple graph, if the graph does not have any loop or double edge. 2. Unsimple graph, if the graph has any loop or double edge.

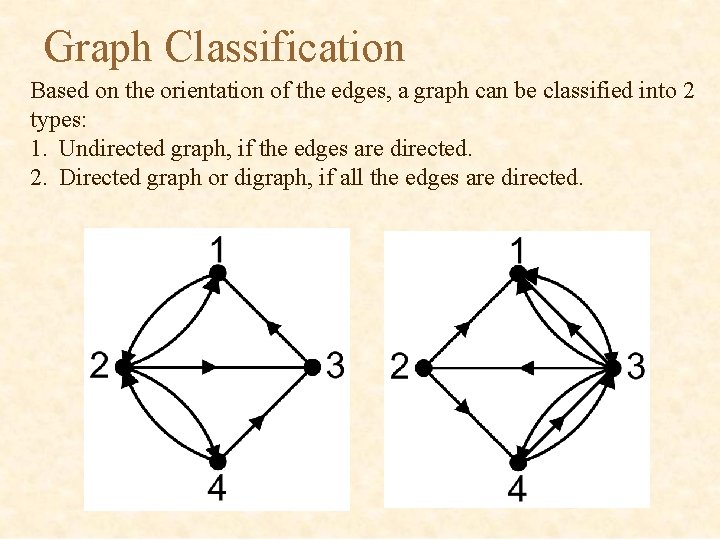
Graph Classification Based on the orientation of the edges, a graph can be classified into 2 types: 1. Undirected graph, if the edges are directed. 2. Directed graph or digraph, if all the edges are directed.

Graph Terminology 1. Adjacency Two vertices are said to be adjacent if they are directly connected through an edge. Observe graph G 1: Vertex 1 is adjacent with vertex 2 and 3. Vertex 1 is not adjacent to vertex 4. G 1

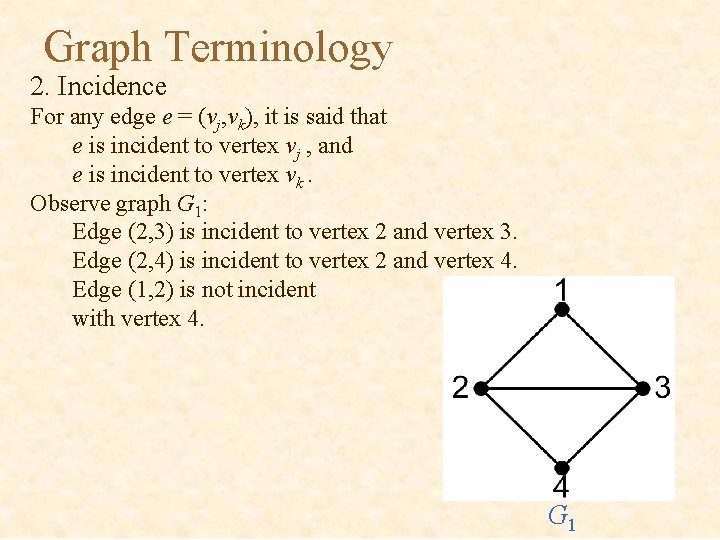
Graph Terminology 2. Incidence For any edge e = (vj, vk), it is said that e is incident to vertex vj , and e is incident to vertex vk. Observe graph G 1: Edge (2, 3) is incident to vertex 2 and vertex 3. Edge (2, 4) is incident to vertex 2 and vertex 4. Edge (1, 2) is not incident with vertex 4. G 1

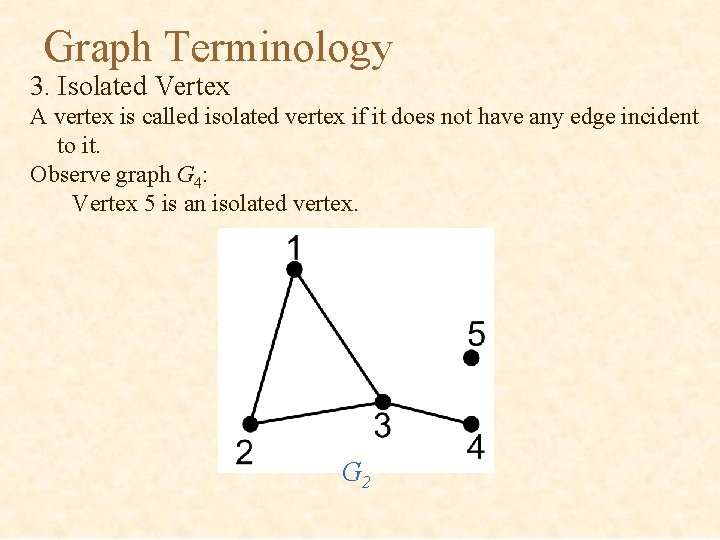
Graph Terminology 3. Isolated Vertex A vertex is called isolated vertex if it does not have any edge incident to it. Observe graph G 4: Vertex 5 is an isolated vertex. G 2

Graph Terminology 4. Empty Graph (Null Graph) An empty graph is a graph whose set of edges is a null set. Observe graph G 5: It is an empty graph (null graph). G 3

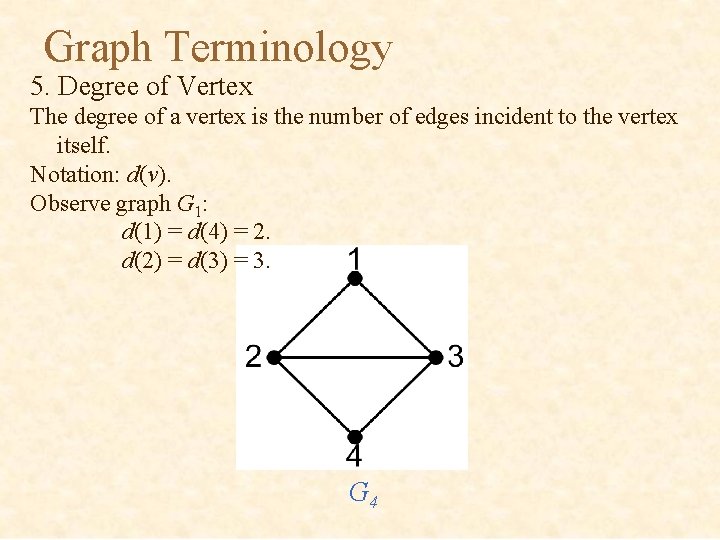
Graph Terminology 5. Degree of Vertex The degree of a vertex is the number of edges incident to the vertex itself. Notation: d(v). Observe graph G 1: d(1) = d(4) = 2. d(2) = d(3) = 3. G 4

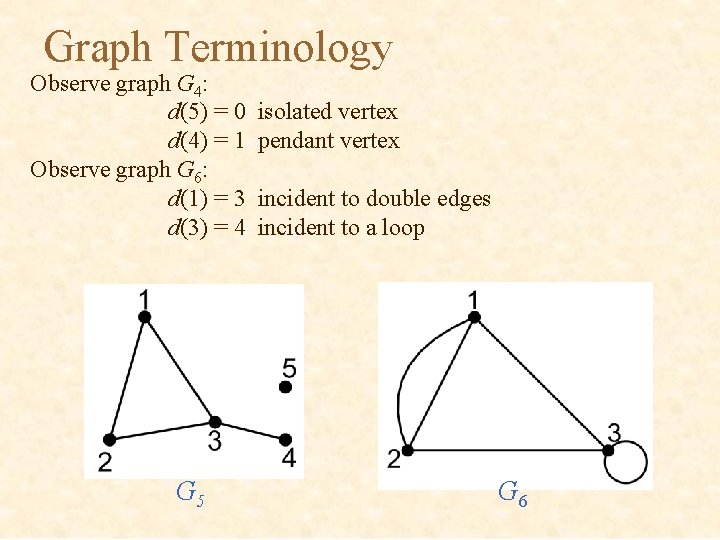
Graph Terminology Observe graph G 4: d(5) = 0 d(4) = 1 Observe graph G 6: d(1) = 3 d(3) = 4 G 5 isolated vertex pendant vertex incident to double edges incident to a loop G 6

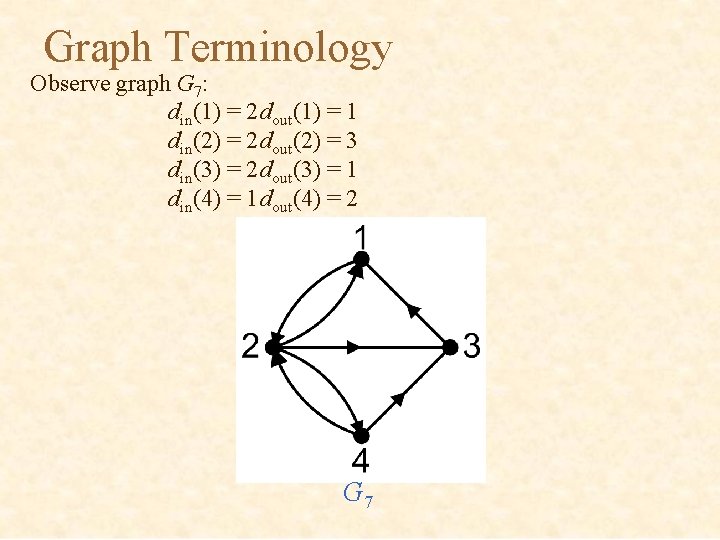
Graph Terminology In a directed graph: din(v) = in-degree = number of arcs arriving to a vertex dout(v) = out-degree = number of arcs departing from a vertex d(v) = din(v) + dout(v)

Graph Terminology Observe graph G 7: din(1) = 2 dout(1) = 1 din(2) = 2 dout(2) = 3 din(3) = 2 dout(3) = 1 din(4) = 1 dout(4) = 2 G 7

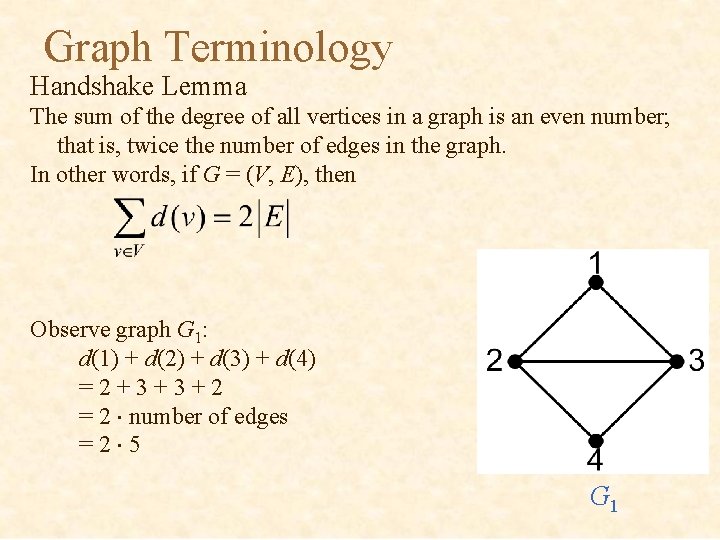
Graph Terminology Handshake Lemma The sum of the degree of all vertices in a graph is an even number; that is, twice the number of edges in the graph. In other words, if G = (V, E), then Observe graph G 1: d(1) + d(2) + d(3) + d(4) =2+3+3+2 = 2 number of edges =2 5 G 1

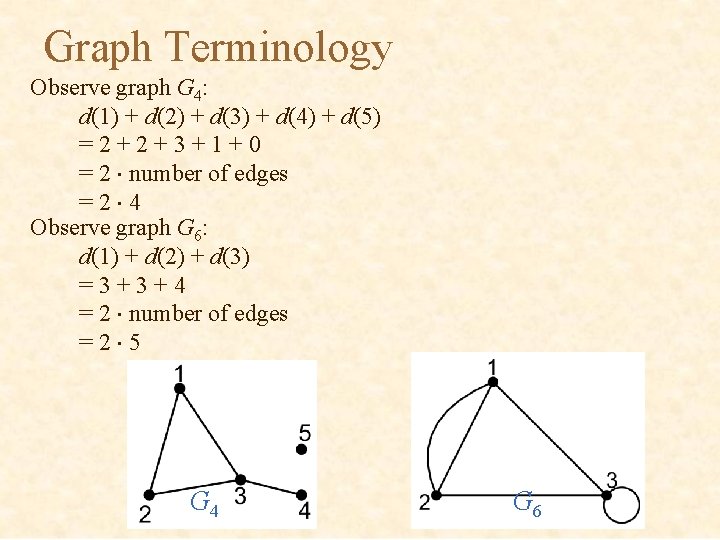
Graph Terminology Observe graph G 4: d(1) + d(2) + d(3) + d(4) + d(5) =2+2+3+1+0 = 2 number of edges =2 4 Observe graph G 6: d(1) + d(2) + d(3) =3+3+4 = 2 number of edges =2 5 G 4 G 6

Graph Terminology Example: A graph has five vertices. Can you draw the graph if the degree of the vertices are: (a) 2, 3, 1, 1, and 2? (b) 2, 3, 3, 4, and 4? Solution: (a) No, because 2 + 3 + 1 + 2 = 9, is an odd number. (b) Yes, because 2 + 3 + 4 = 16, is an even number.

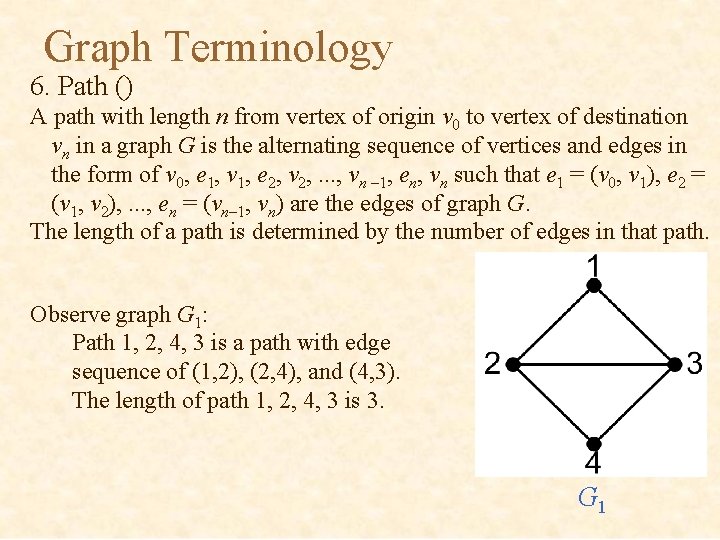
Graph Terminology 6. Path () A path with length n from vertex of origin v 0 to vertex of destination vn in a graph G is the alternating sequence of vertices and edges in the form of v 0, e 1, v 1, e 2, v 2, . . . , vn – 1, en, vn such that e 1 = (v 0, v 1), e 2 = (v 1, v 2), . . . , en = (vn– 1, vn) are the edges of graph G. The length of a path is determined by the number of edges in that path. Observe graph G 1: Path 1, 2, 4, 3 is a path with edge sequence of (1, 2), (2, 4), and (4, 3). The length of path 1, 2, 4, 3 is 3. G 1

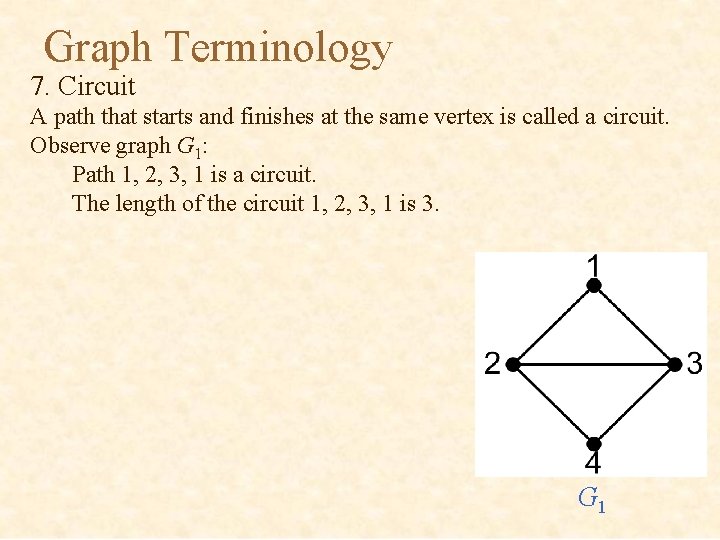
Graph Terminology 7. Circuit A path that starts and finishes at the same vertex is called a circuit. Observe graph G 1: Path 1, 2, 3, 1 is a circuit. The length of the circuit 1, 2, 3, 1 is 3. G 1

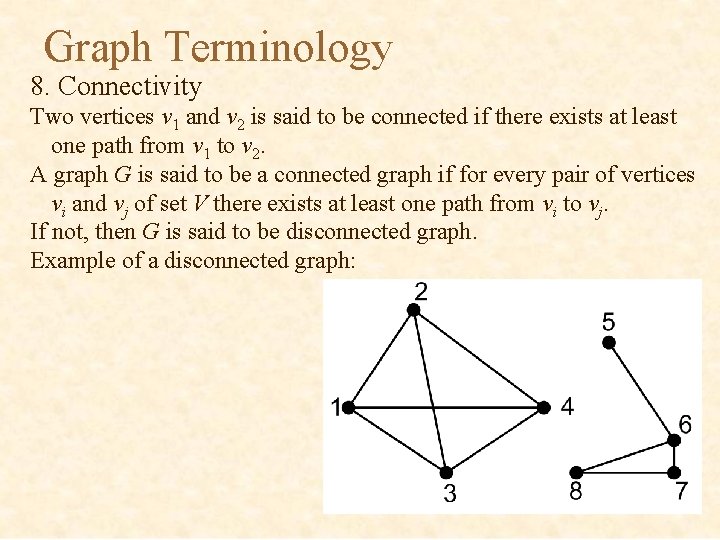
Graph Terminology 8. Connectivity Two vertices v 1 and v 2 is said to be connected if there exists at least one path from v 1 to v 2. A graph G is said to be a connected graph if for every pair of vertices vi and vj of set V there exists at least one path from vi to vj. If not, then G is said to be disconnected graph. Example of a disconnected graph:

Graph Terminology A directed graph G is said to be connected if its non-directed graph is connected (Note: the non-directed graph of a directed graph G is obtained by omitting all arrow heads).

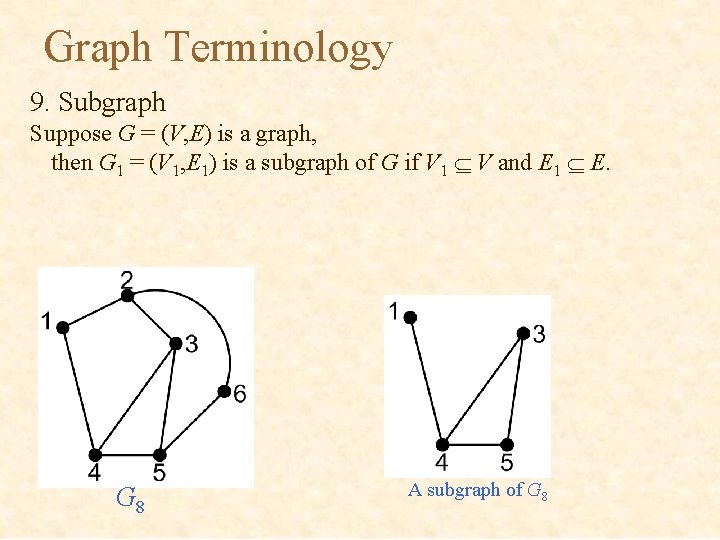
Graph Terminology 9. Subgraph Suppose G = (V, E) is a graph, then G 1 = (V 1, E 1) is a subgraph of G if V 1 V and E 1 E. G 8 A subgraph of G 8

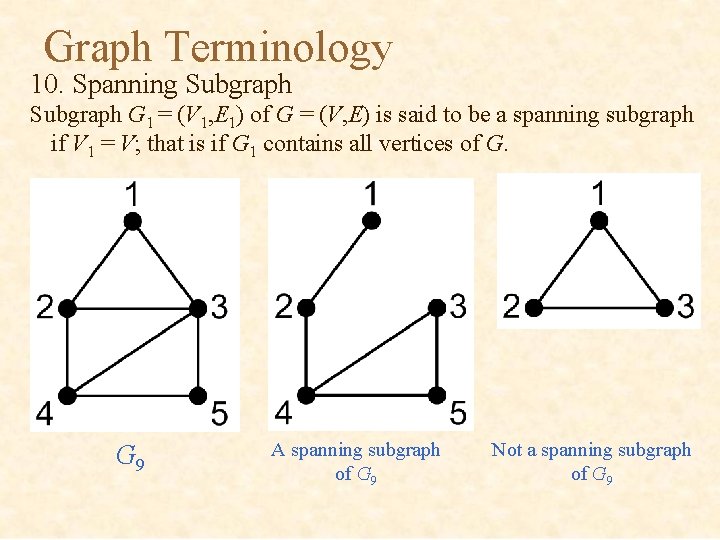
Graph Terminology 10. Spanning Subgraph G 1 = (V 1, E 1) of G = (V, E) is said to be a spanning subgraph if V 1 = V; that is if G 1 contains all vertices of G. G 9 A spanning subgraph of G 9 Not a spanning subgraph of G 9

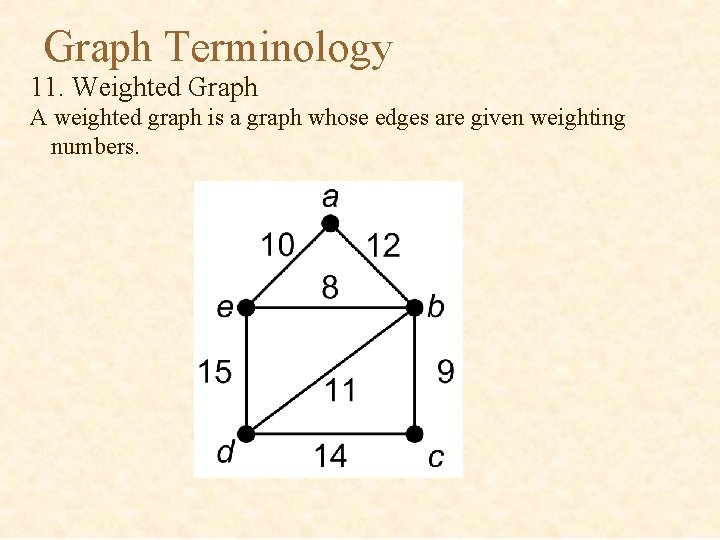
Graph Terminology 11. Weighted Graph A weighted graph is a graph whose edges are given weighting numbers.

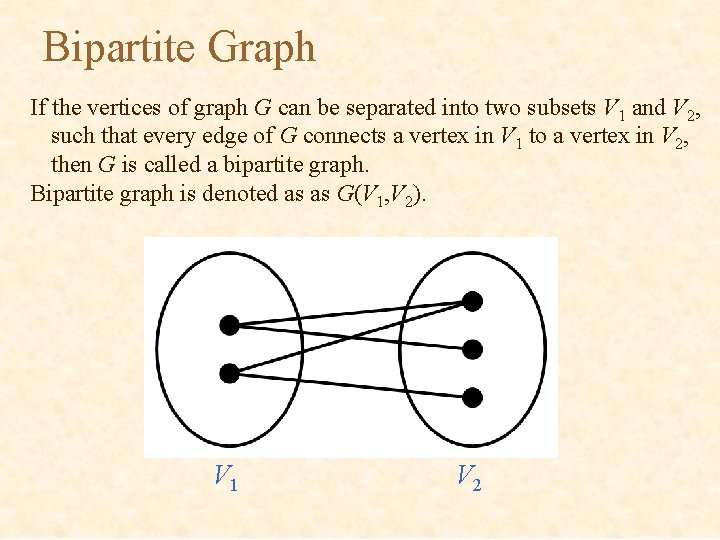
Bipartite Graph If the vertices of graph G can be separated into two subsets V 1 and V 2, such that every edge of G connects a vertex in V 1 to a vertex in V 2, then G is called a bipartite graph. Bipartite graph is denoted as as G(V 1, V 2). V 1 V 2

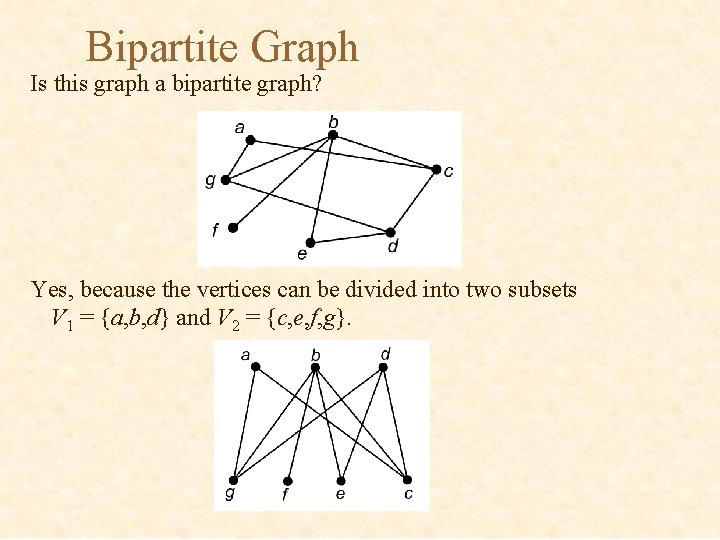
Bipartite Graph Is this graph a bipartite graph? Yes, because the vertices can be divided into two subsets V 1 = {a, b, d} and V 2 = {c, e, f, g}.

Euler Path and Euler Circuit An Euler path in a graph is a path that contains every edge of the graph exactly once. An Euler circuit in a graph is a circuit that contains every edge of a graph exactly once. A graph that contains Euler path is also called semi-Eulerian graph. A graph that contains Euler circuit is also called Eulerian graph.

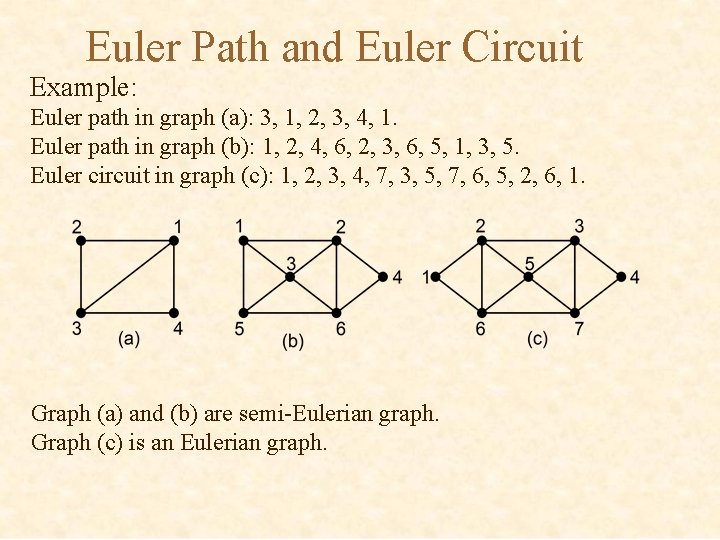
Euler Path and Euler Circuit Example: Euler path in graph (a): 3, 1, 2, 3, 4, 1. Euler path in graph (b): 1, 2, 4, 6, 2, 3, 6, 5, 1, 3, 5. Euler circuit in graph (c): 1, 2, 3, 4, 7, 3, 5, 7, 6, 5, 2, 6, 1. Graph (a) and (b) are semi-Eulerian graph. Graph (c) is an Eulerian graph.

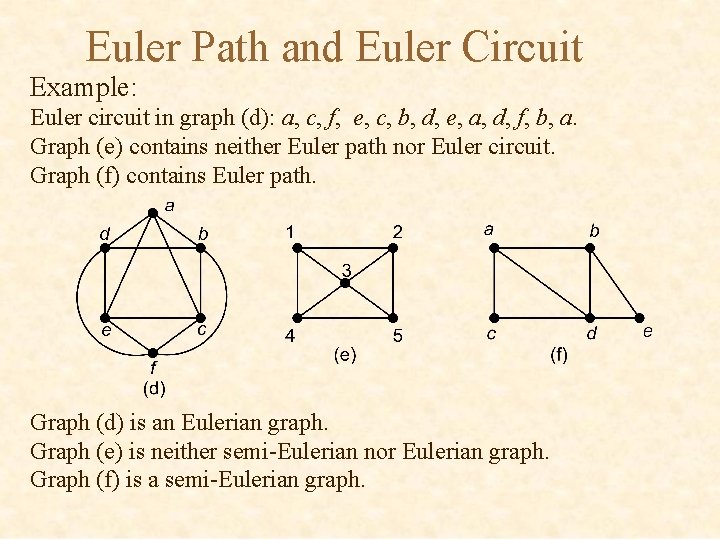
Euler Path and Euler Circuit Example: Euler circuit in graph (d): a, c, f, e, c, b, d, e, a, d, f, b, a. Graph (e) contains neither Euler path nor Euler circuit. Graph (f) contains Euler path. Graph (d) is an Eulerian graph. Graph (e) is neither semi-Eulerian nor Eulerian graph. Graph (f) is a semi-Eulerian graph.

Euler Path and Euler Circuit Theorem: An undirected graph G contains Euler path if and only if it is connected and has two vertices of odd degree or does not have any vertices of odd degree at all. Theorem: An undirected graph G contains Euler circuit if and only if it is connected and each of its vertices has even degree. In other words: An undirected graph G is an Eulerian graph if and only if the degree of every vertex is even.

Euler Path and Euler Circuit Theorem: A directed graph G contains Euler path if and only if G is connected and for each vertex, the in-degree and out-degree are the same, except two vertices, where the first vertex’s out-degree is one greater than the in-degree and the second vertex’s in-degree is one greater than the out -degree. Theorem: A directed graph G contains Euler circuit if and only if G is connected and for each vertex, the in-degree and out-degree are the same.

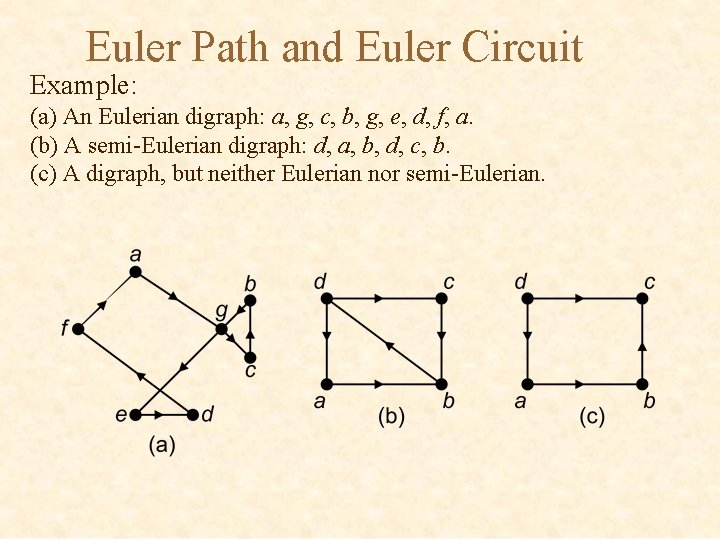
Euler Path and Euler Circuit Example: (a) An Eulerian digraph: a, g, c, b, g, e, d, f, a. (b) A semi-Eulerian digraph: d, a, b, d, c, b. (c) A digraph, but neither Eulerian nor semi-Eulerian.

Euler Path and Euler Circuit Example: Is it possible to draw the graph below, by starting from any vertex, and without drawing any line twice? Solution: Yes, possible. All the vertices in the undirected graph above are of even degree. Therefore, the Euler circuit can be drawn. The graph is an Eulerian graph.

Hamilton Path and Hamilton Circuit A Hamilton path in a graph is a path that passes every vertex of the graph exactly once. A Hamilton circuit in a graph is a circuit that passes every vertex of the graph exactly once, except one vertex which is the origin and (at the same time) the destination, is passed twice. A graph that contains Hamilton path is also called semi-Hamiltonian graph. A graph that contains Hamilton circuit is also called Hamiltonian graph.

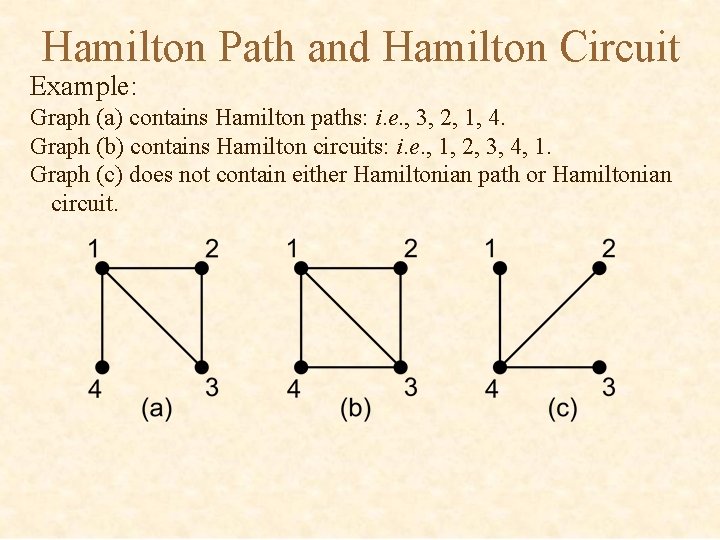
Hamilton Path and Hamilton Circuit Example: Graph (a) contains Hamilton paths: i. e. , 3, 2, 1, 4. Graph (b) contains Hamilton circuits: i. e. , 1, 2, 3, 4, 1. Graph (c) does not contain either Hamiltonian path or Hamiltonian circuit.

Hamilton Path and Hamilton Circuit Theorem: A sufficient condition for a graph G with the number of vertices n 3 to be a Hamiltonian graph is that the degree of each vertex v in G to be at least n/2, or d(v) n/2.

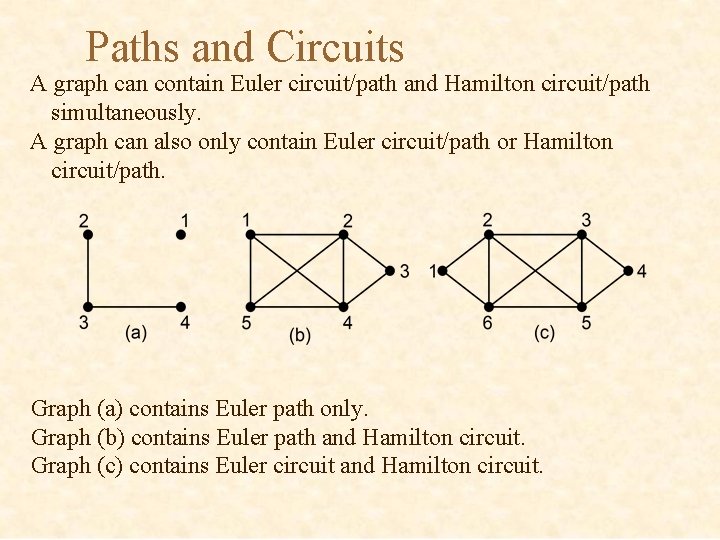
Paths and Circuits A graph can contain Euler circuit/path and Hamilton circuit/path simultaneously. A graph can also only contain Euler circuit/path or Hamilton circuit/path. Graph (a) contains Euler path only. Graph (b) contains Euler path and Hamilton circuit. Graph (c) contains Euler circuit and Hamilton circuit.

Applications of Graphs Travelling salesman problem. Chinese postman problem. Graph coloring.

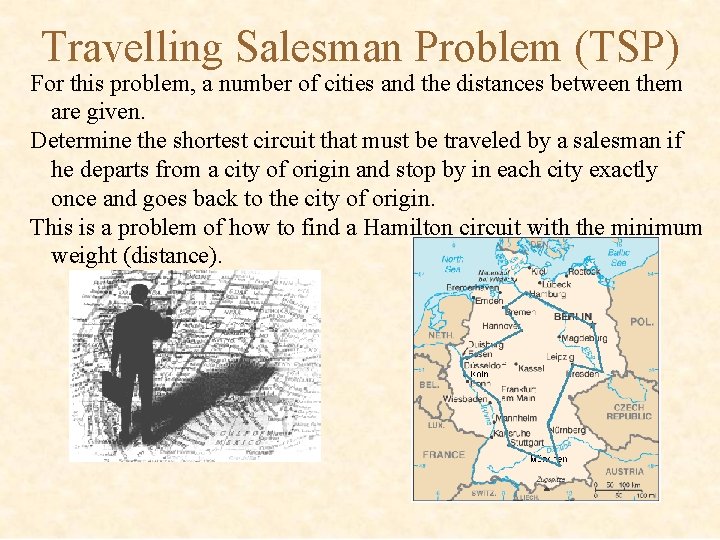
Travelling Salesman Problem (TSP) For this problem, a number of cities and the distances between them are given. Determine the shortest circuit that must be traveled by a salesman if he departs from a city of origin and stop by in each city exactly once and goes back to the city of origin. This is a problem of how to find a Hamilton circuit with the minimum weight (distance).

Applications of TSP Mr. Postman collects the letters for mailboxes which are distributed in n locations in a certain town. The robot arm fastens n bolts of a car in an assembly line. Production process of n different products in one cycle.

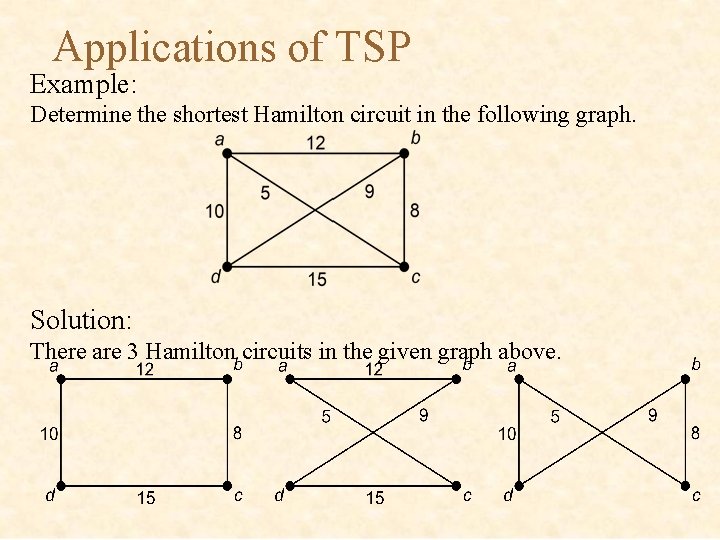
Applications of TSP Example: Determine the shortest Hamilton circuit in the following graph. Solution: There are 3 Hamilton circuits in the given graph above.

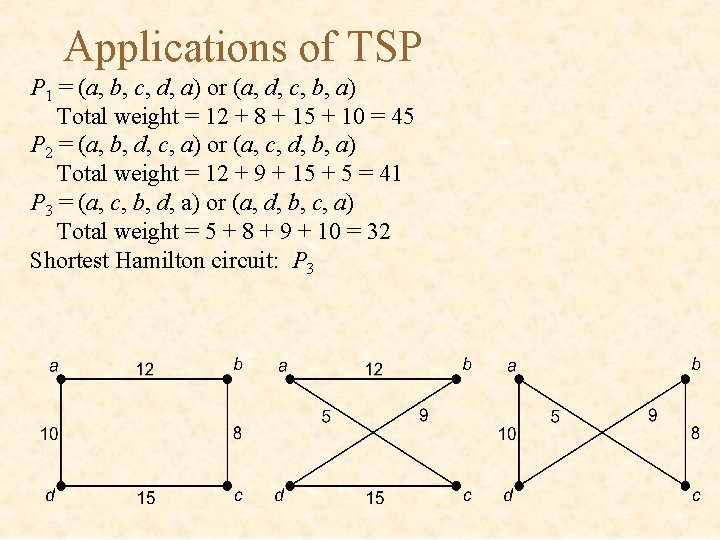
Applications of TSP P 1 = (a, b, c, d, a) or (a, d, c, b, a) Total weight = 12 + 8 + 15 + 10 = 45 P 2 = (a, b, d, c, a) or (a, c, d, b, a) Total weight = 12 + 9 + 15 + 5 = 41 P 3 = (a, c, b, d, a) or (a, d, b, c, a) Total weight = 5 + 8 + 9 + 10 = 32 Shortest Hamilton circuit: P 3

Chinese Postman Problem The problem was first discussed by Mei Gan in 1962. Problem: A postman will deliver the letters to the addresses in a part of a city. How should he plan the route of his journey so that he can pass each street exactly once and go back to the place where he starts his journey? This is a problem of how to find an Euler circuit in a graph.

Chinese Postman Problem If the graph of the problem is an Eulerian graph, then the Euler circuit can easily be found. If the graph of the problem is not an Eulerian graph, then some edges in the graph must be passed more than once. So, the postman must find a circuit that passes every street at least once with the shortest distance possible. Chinese Postman Problem becomes: A postman will deliver the letters to the addresses in a part of a city. How should he plan his route so that: The route has the shortest distance. The postman passes every street at least once. The postman goes back to his original position.

Chinese Postman Problem Example: Determine the best path that can be chosen by a postman so that he can pass every edge of the following graph at least once. Solution: The path that should be chosen by the postman is: A, B, C, D, E, F, C, E, B, F, A Weight = 2 + 8 + 1 + 2 + 5 + 4 + 8 + 3 + 6 = 43.

Examples

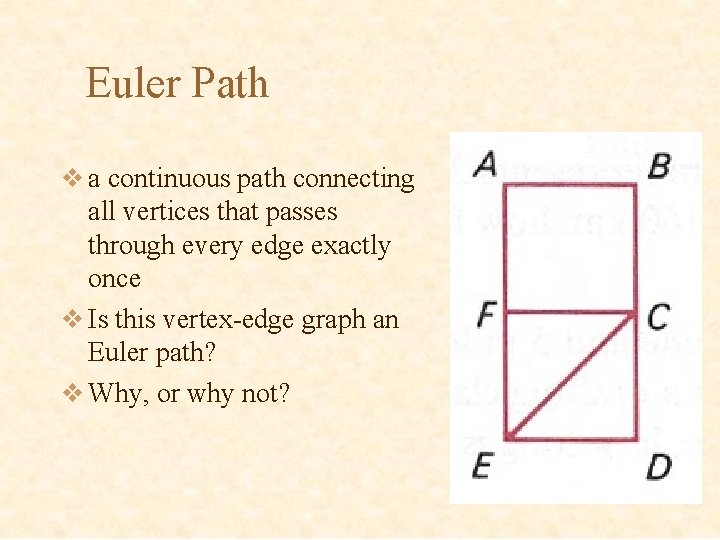
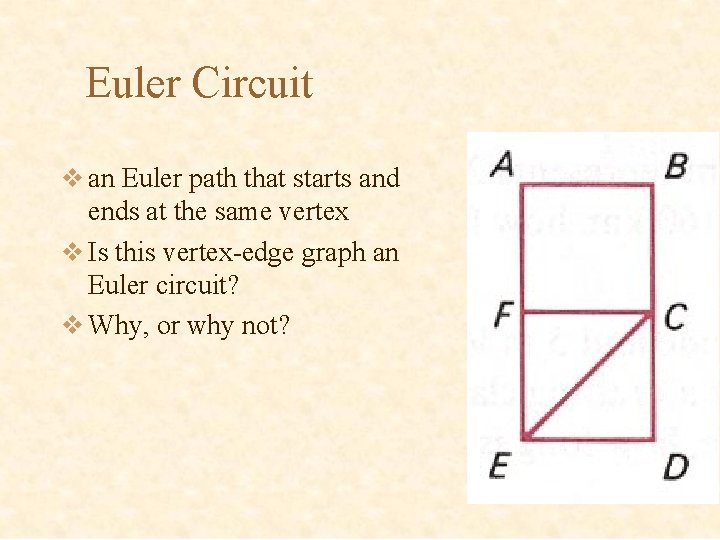
Euler Path v a continuous path connecting all vertices that passes through every edge exactly once v Is this vertex-edge graph an Euler path? v Why, or why not?

Euler Circuit v an Euler path that starts and ends at the same vertex v Is this vertex-edge graph an Euler circuit? v Why, or why not?

Another Example v Is this vertex-edge graph an Euler path? v Why or why not? v Is this vertex-edge graph an Euler circuit? v Why, or why not?

Euler’s Theorem, or Rules • If a graph has more than two odd vertices, then it does not have an Euler path. • If a graph has two or fewer odd vertices, then it has at least one Euler path. • If a graph has any odd vertices, then it cannot have an Euler circuit. • If every vertex in a graph is even, then it has at least one Euler circuit.

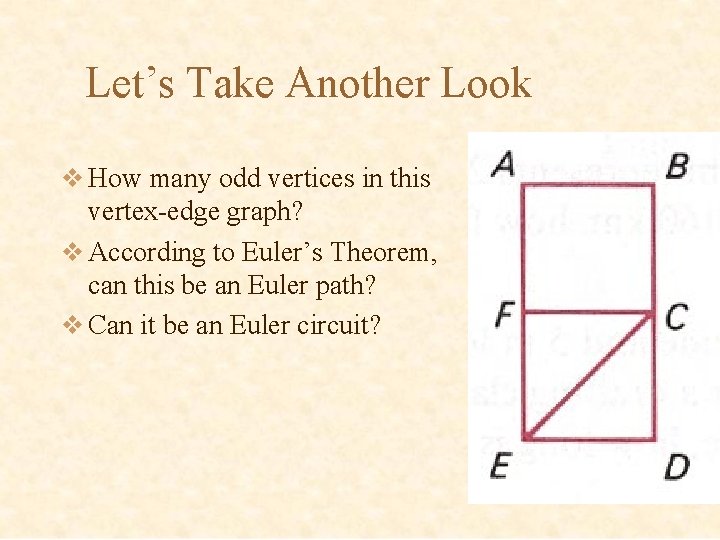
Let’s Take Another Look v How many odd vertices in this vertex-edge graph? v According to Euler’s Theorem, can this be an Euler path? v Can it be an Euler circuit?

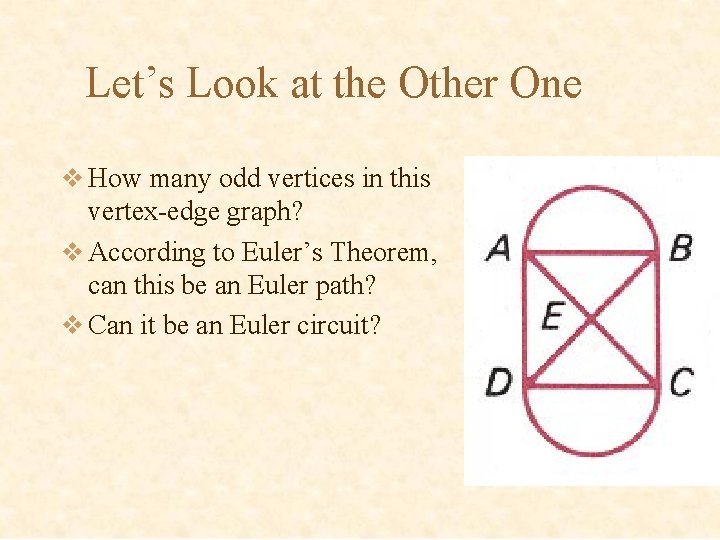
Let’s Look at the Other One v How many odd vertices in this vertex-edge graph? v According to Euler’s Theorem, can this be an Euler path? v Can it be an Euler circuit?

Pencil Drawing Problem -Euler Paths Which of the following pictures can be drawn on paper without ever lifting the pencil and without retracing over any segment?

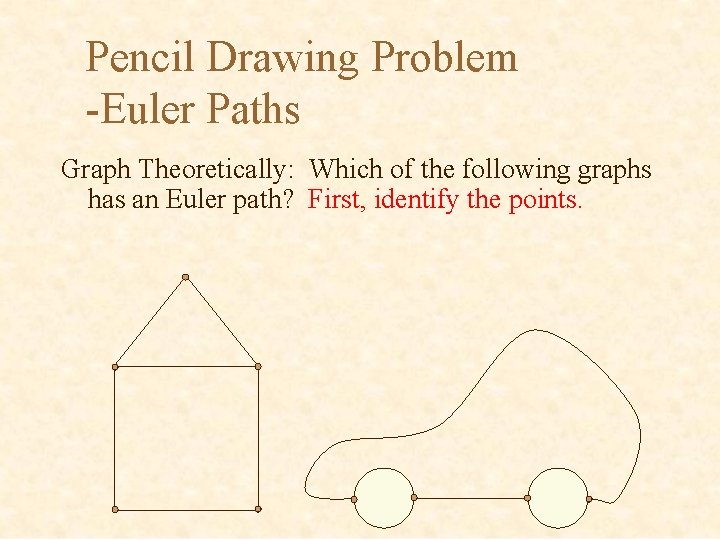
Pencil Drawing Problem -Euler Paths Graph Theoretically: Which of the following graphs has an Euler path? First, identify the points.

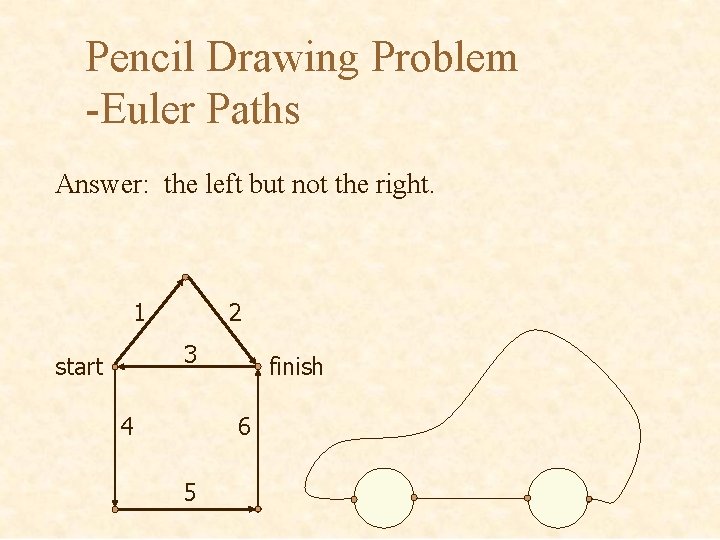
Pencil Drawing Problem -Euler Paths Answer: the left but not the right. 1 2 3 start 4 finish 6 5

Hamilton Circuit A Hamilton circuit in a graph is a circuit that visits each vertex exactly once (returning to the starting vertex to complete the circuit). © 2008 Pearson Addison-Wesley. All rights reserved 15 -3 -60

Example: Identifying Hamilton Circuits Refer to the graph below. Which of the following are Hamilton circuits? C B A F E D

Example: Identifying Hamilton Circuits Solution a) It is a Hamilton circuit for the graph. b) It is not a Hamilton circuit since it visits B more than once. c) It is not a Hamilton circuit since it does not visit all the vertices.