Theory of Computation Transition Graph Definition A Transition

Theory of Computation

Transition Graph Definition: A Transition graph (TG), is a collection of the following: 1) Finite number of states, at least one of which is start state and some (maybe none) final states. 2)Finite set of input letters (Σ) from which input strings are formed. 3)Finite set of transitions that show to go from one state to another based on reading specified substrings of input letters, possibly even the null string: Λ. 2

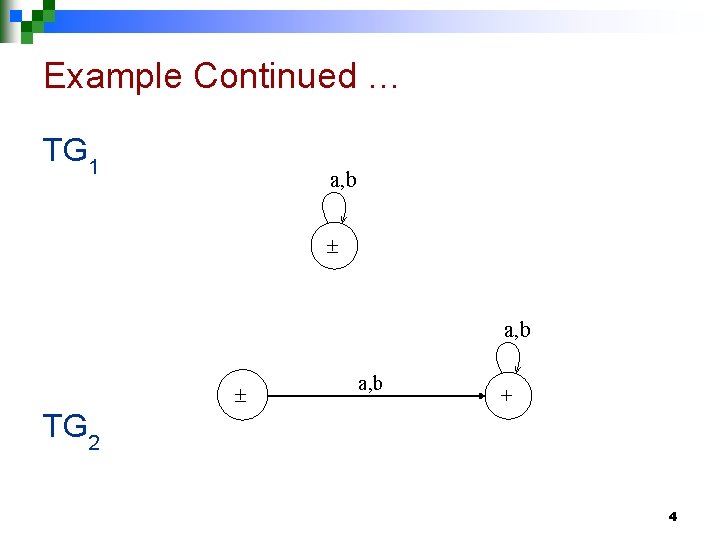
Example n Consider the Language L , defined over Σ = {a, b} of all strings including Λ. The language L may be accepted by the following TG a, b - a, b Λ + The language L may also be accepted by the following TG 3

Example Continued … TG 1 a, b + TG 2 4

Example Consider the language L of strings, defined over Σ={a, b}, starting with b. The language L may be expressed by RE b(a + b)* , may be accepted by the following TG a, b –– b + 5

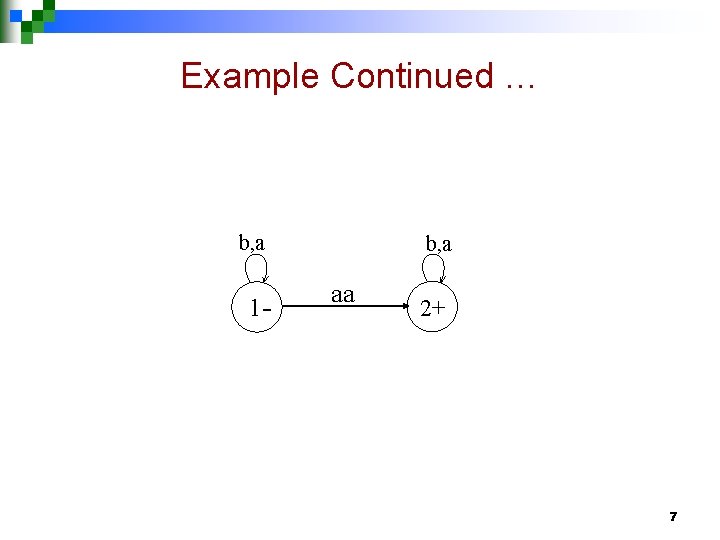
Example Consider the Language L of strings, defined over Σ = {a, b}, containing double a. The language L may be expressed by the following regular expression * * (a+b) (aa) (a+b). This language may be accepted by the following TG 6

Example Continued … b, a 1 - b, a aa 2+ 7

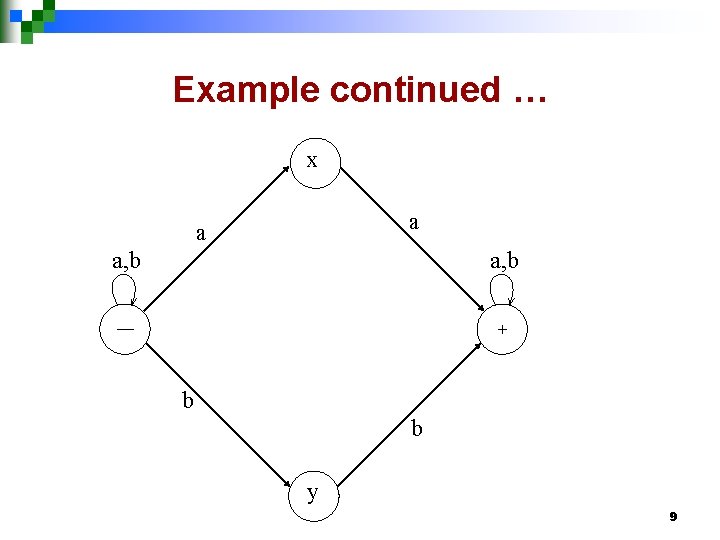
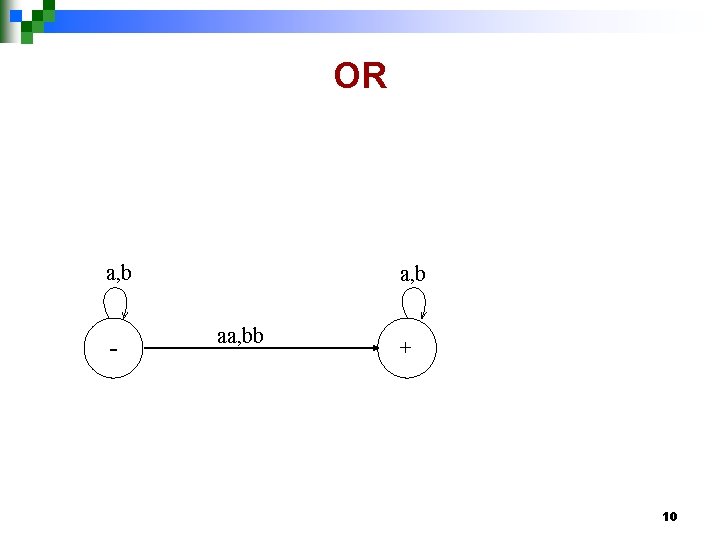
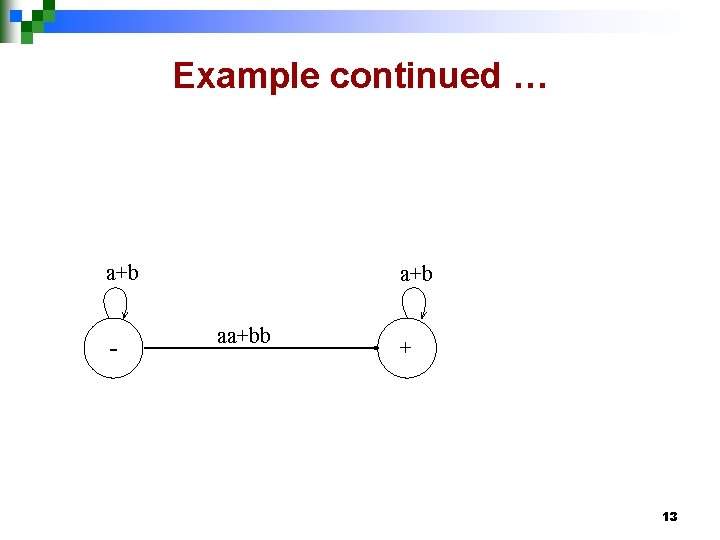
Example Consider the language L of strings, defined over Σ={a, b}, having double a or double b. The language L can be expressed by RE (a+b)* (aa + bb) (a+b)*. The above language may also be expressed by the following TGs. 8

Example continued … x a a a, b –– + b b y 9

OR a, b - a, b aa, bb + 10

Generalized Transition Graphs A generalized transition graph (GTG) is a collection of three things 1) Finite number of states, at least one of which is start state and some (maybe none) final states. 2) Finite set of input letters (Σ) from which input strings are formed. 3) Directed edges connecting some pair of states labeled with regular expression. 11

Example Consider the language L of strings, defined over Σ={a, b}, containing double a or double b. The language L can be expressed by the following regular expression * * (a+b) (aa + bb) (a+b) The language L may be accepted by the following GTG. 12

Example continued … a+b - a+b aa+bb + 13

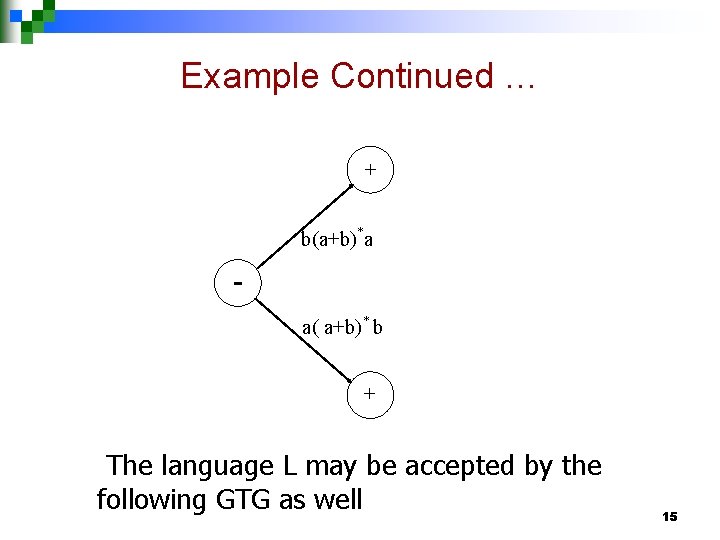
Example Consider the language L of strings, defined over Σ = {a, b}, beginning and ending in different letters. The language L may be expressed by RE a(a + b)*b + b(a + b)*a The language L may be accepted by the following GTG 14

Example Continued … + b(a+b)*a a( a+b)* b + The language L may be accepted by the following GTG as well 15

Example Continued … - b(a+b)*a + a( a+b)* b + 16

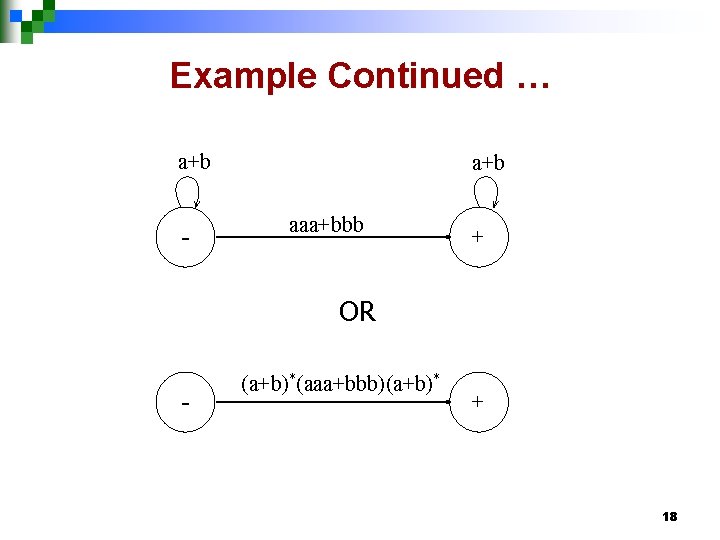
Example Consider the language L of strings, defined over Σ={a, b}, having triple a or triple b. The language L may be expressed by RE * * (a+b) (aaa + bbb) (a+b) This language may be accepted by the following GTG 17

Example Continued … a+b - a+b aaa+bbb + OR - (a+b)*(aaa+bbb)(a+b)* + 18

Kleene’s Theorem n 1. 2. 3. If a language is expressed by FA or TG or RE then it can also be expressed by other two as well. theorem is proved by proving the following three parts 19

Kleene’s Theorem continued … Kleene’s Theorem Part I If a language is accepted by an FA then it can be accepted by a TG as well. Kleene’s Theorem Part II If a language is accepted by a TG then it can be expressed by an RE as well. Kleene’s Theorem Part III If a language is expressed by an RE then it can also be accepted by an FA. 20

Kleene’s Theorem continued … Proof(Kleene’s Theorem Part I) Since every FA can be considered to be a TG, therefore there is nothing to prove. 21

Kleene’s Theorem continued … Proof(Kleene’s Theorem Part II) To prove part II of theorem, an algorithm consisting of different steps is explained showing how a RE can be obtained corresponding to the given TG. 22

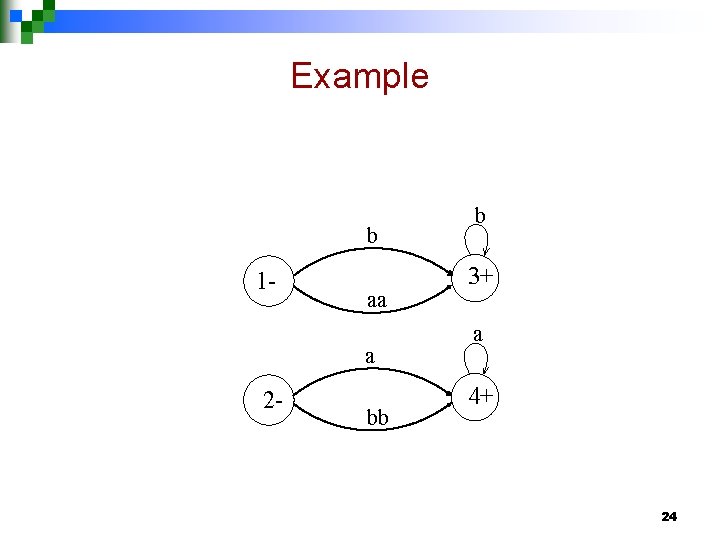
Kleene’s Theorem part II continued … Step 1 If a TG has more than one start state, then introduce a new start state connecting the new state to the old start states by the transitions labeled by Λ and make the old start states the non-start states. 23

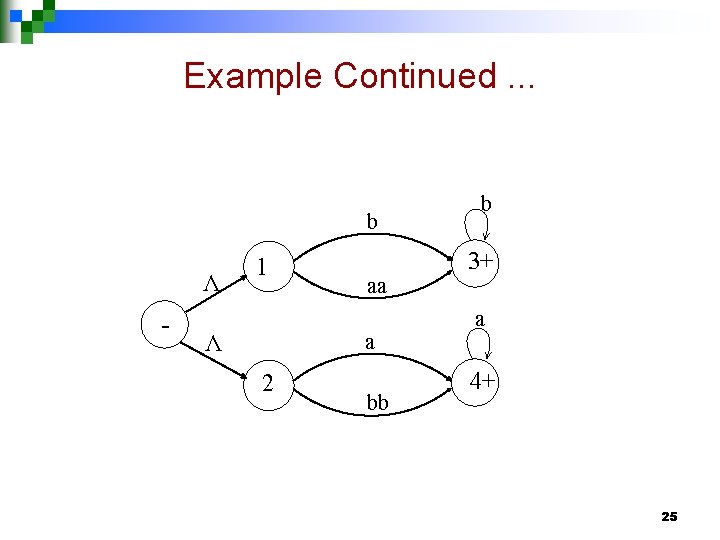
Example b 1 - aa a 2 - bb b 3+ a 4+ 24

Example Continued. . . b Λ - 1 aa a Λ 2 bb b 3+ a 4+ 25

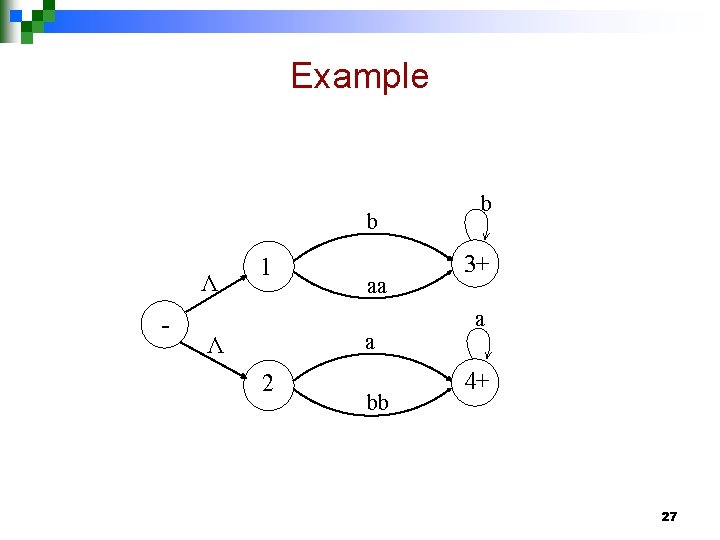
Kleene’s Theorem part II continued … Step 2: If a TG has more than one final state, then introduce a new final state, connecting the old final states to the new final state by the transitions labeled by Λ. 26

Example b Λ - 1 aa a Λ 2 bb b 3+ a 4+ 27

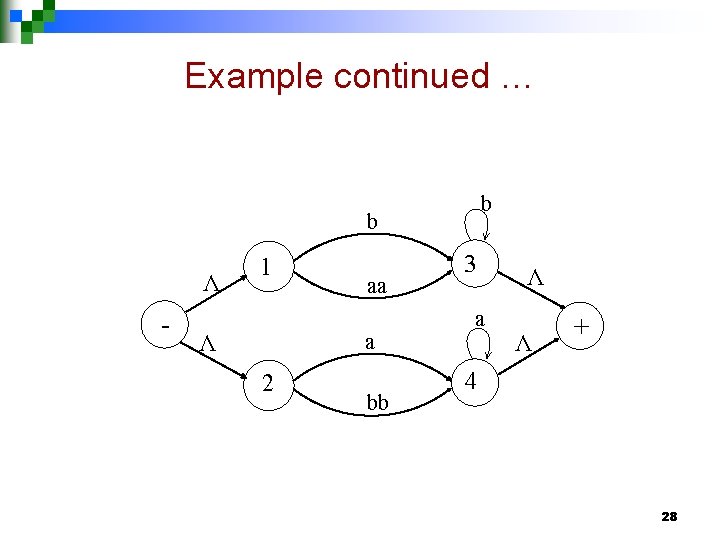
Example continued … b Λ - 1 aa a Λ 2 bb 3 a Λ Λ + b 4 28

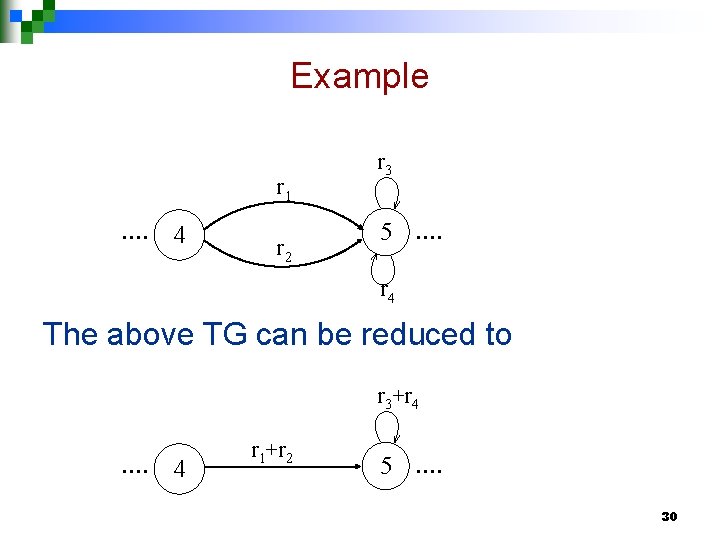
Kleene’s Theorem part II continued … Step 3: If a state has more than one incoming transition edge labeled by the corresponding REs, from the same state (including the possibility of loops at a state), then replace all these transition edges with a single transition edge labeled by the sum of corresponding REs. 29

Example r 1 …. 4 r 2 r 3 5 …. r 4 The above TG can be reduced to r 3+r 4 …. 4 r 1+r 2 5 …. 30

Note n The step 3 can be generalized to any finite number of transitions as shown below r 1 5 …. . … …. r 2 rn The above TG can be reduced to r +r + … +r 1 …. 2 n 5 …. 31

Kleene’s Theorem part II continued … Step 4 (bypass and state elimination) If three states in a TG are connected in a sequence then eliminate the middle state and connect the first state with the third by a single transition (including loops) labeled by the RE, which is the concatenation of corresponding two REs in the existing sequence. 32

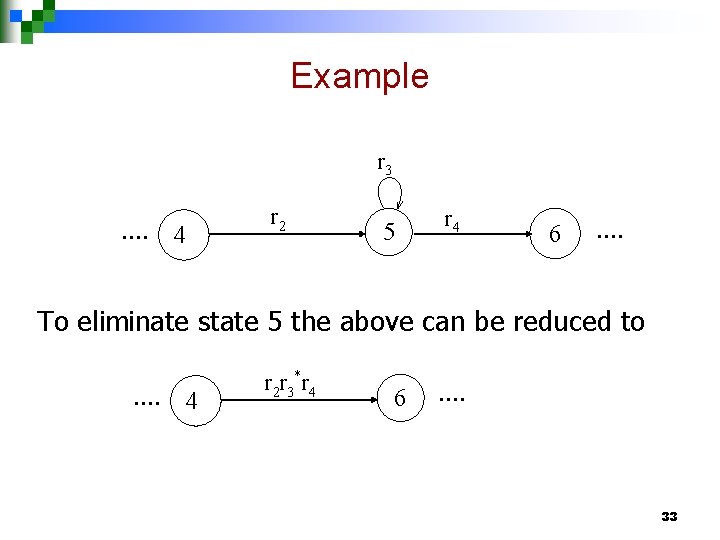
Example r 3 …. 4 r 2 5 r 4 6 …. To eliminate state 5 the above can be reduced to …. 4 r 2 r 3*r 4 6 …. 33

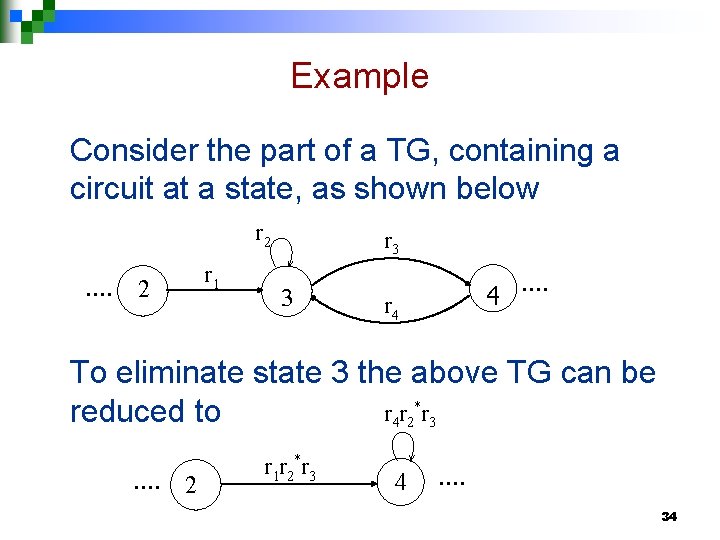
Example Consider the part of a TG, containing a circuit at a state, as shown below r 2 …. r 1 2 r 3 3 4 r 4 …. To eliminate state 3 the above TG can be r 4 r 2*r 3 reduced to …. 2 r 1 r 2*r 3 4 …. 34

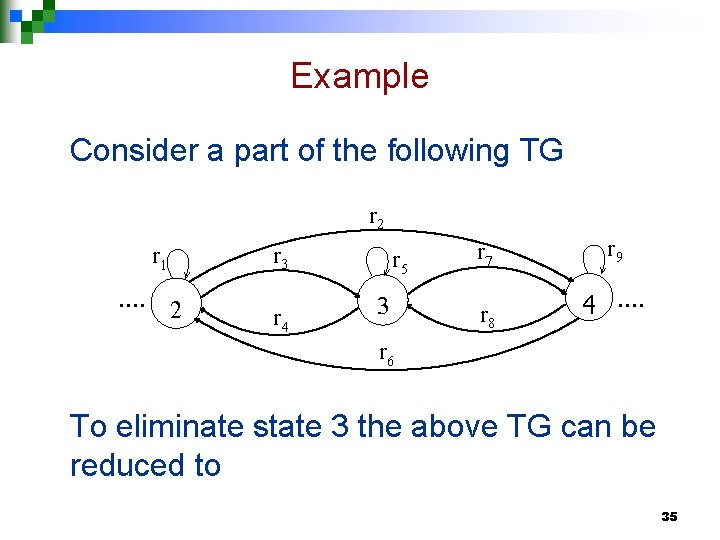
Example Consider a part of the following TG r 2 r 3 r 1 …. 2 r 4 r 5 3 r 7 r 8 r 9 4 …. r 6 To eliminate state 3 the above TG can be reduced to 35

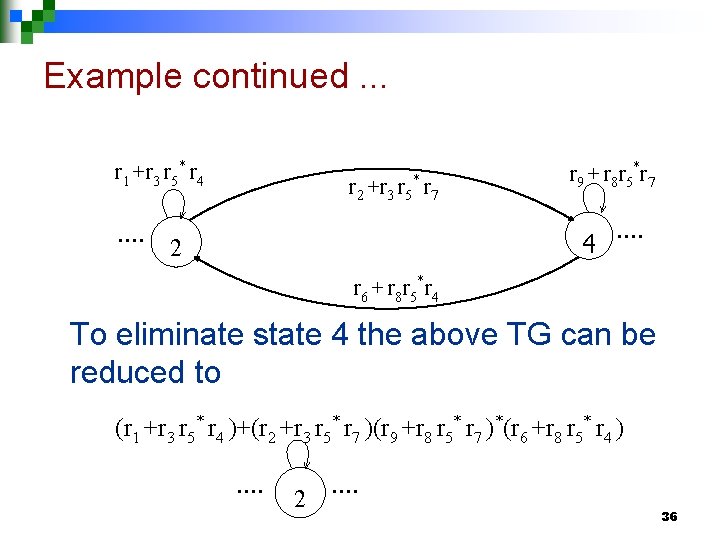
Example continued. . . r 1 +r 3 r 5* r 4 …. r 2 +r 3 r 5* r 7 r 9 + r 8 r 5*r 7 4 2 …. r 6 + r 8 r 5*r 4 To eliminate state 4 the above TG can be reduced to (r 1 +r 3 r 5* r 4 )+(r 2 +r 3 r 5* r 7 )(r 9 +r 8 r 5* r 7 )*(r 6 +r 8 r 5* r 4 ) …. 2 …. 36

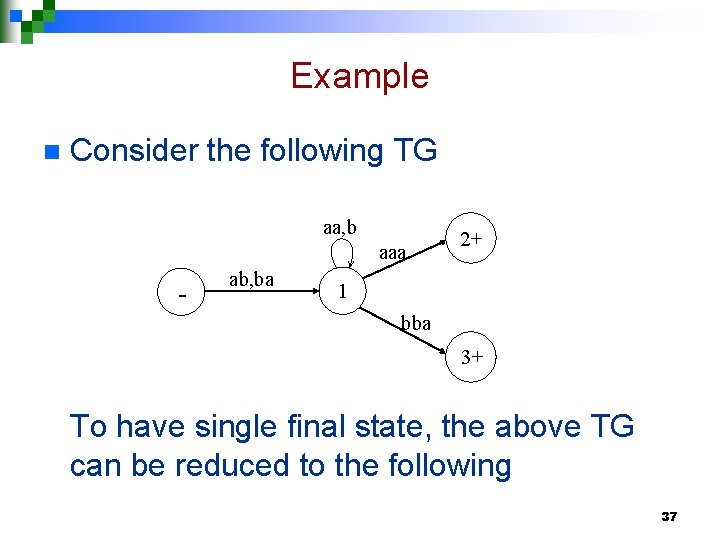
Example n Consider the following TG aa, b aaa - ab, ba 2+ 1 bba 3+ To have single final state, the above TG can be reduced to the following 37

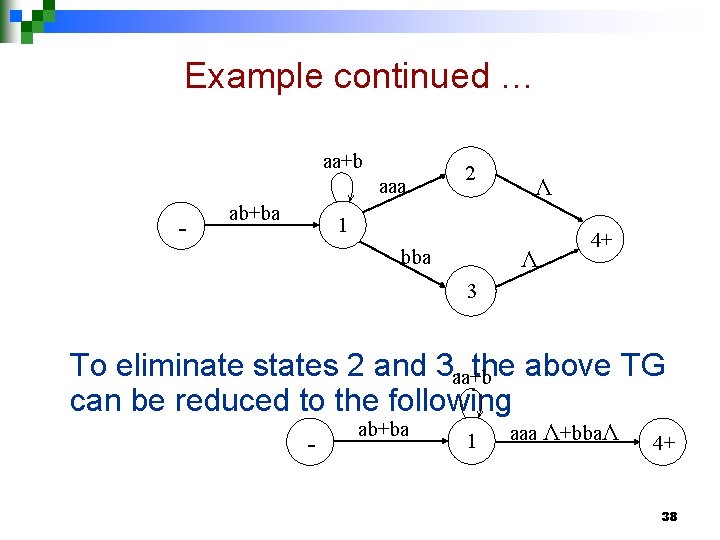
Example continued … aa+b aaa - ab+ba 2 Λ 1 bba Λ 4+ 3 To eliminate states 2 and 3, aa+b the above TG can be reduced to the following - ab+ba 1 aaa Λ+bbaΛ 4+ 38

Example continued … To eliminate state 1 the above TG can be reduced to the following - (ab+ba)(aa+b)*(aaa+bba) + Hence the required RE is (ab+ba)(aa+b)*(aaa+bba) 39

Kleene’s Theorem Part III Continued … If r 1 and r 2 are regular expressions then their sum, concatenation and closure also regular expressions 40

Kleene’s Theorem Part III Continued … n Method 1 (Union of two FAs): Using the FAs corresponding to r 1 and r 2 an FA can be built, corresponding to r 1+r 2. This method can be developed considering the following examples 41

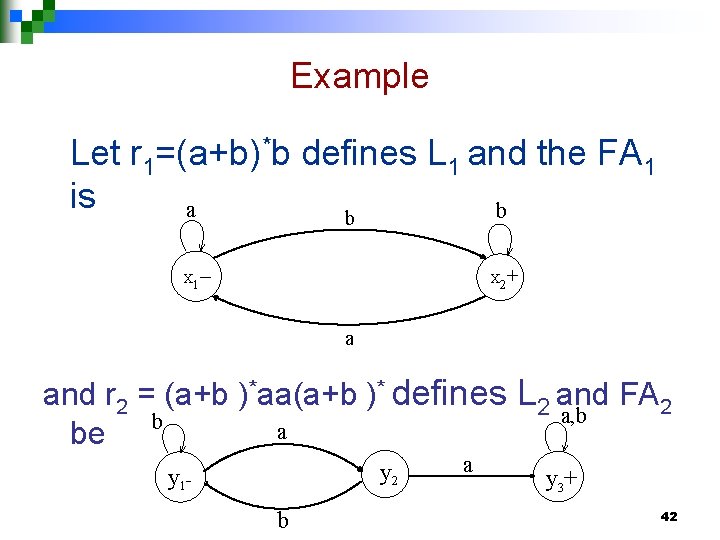
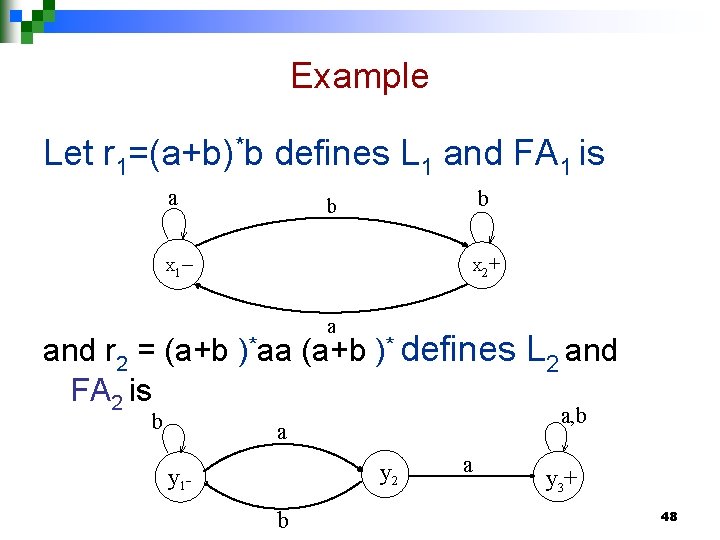
Example Let r 1=(a+b)*b defines L 1 and the FA 1 is a b b – + X 1 X 2 a and r 2 = (a+b )*aa(a+b )* defines L 2 and FA 2 a, b b a be y 2 y 1 b a y 3+ 42

Sum of two FAs Continued … Let FA 3 be an FA corresponding to r 1+ r 2, then the initial state of FA 3 must correspond to the initial state of FA 1 or the initial state of FA 2. Since the language corresponding to r 1+r 2 is the union of corresponding languages L 1 and L 2, consists of the strings belonging to L 1 or L 2 or both, therefore, a final state of FA 3 must correspond to a final state of FA 1 or FA 2 or both. 43

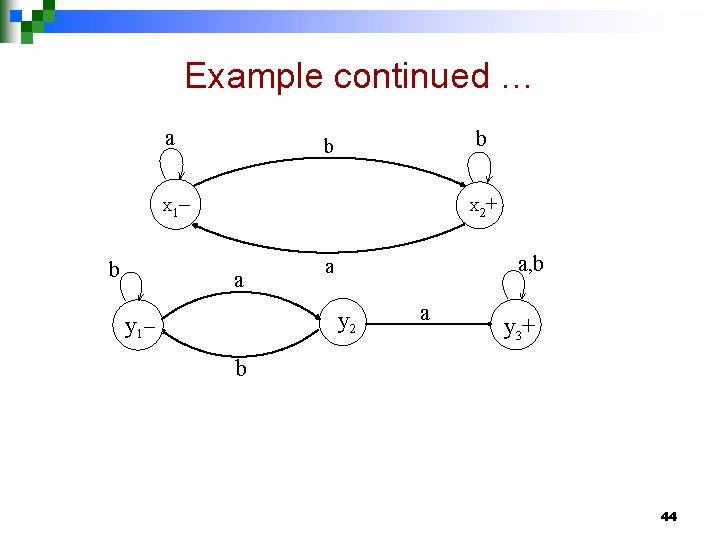
Example continued … a b b – + X 1 b X 2 a a, b a y 2 y 1– a y 3+ b 44

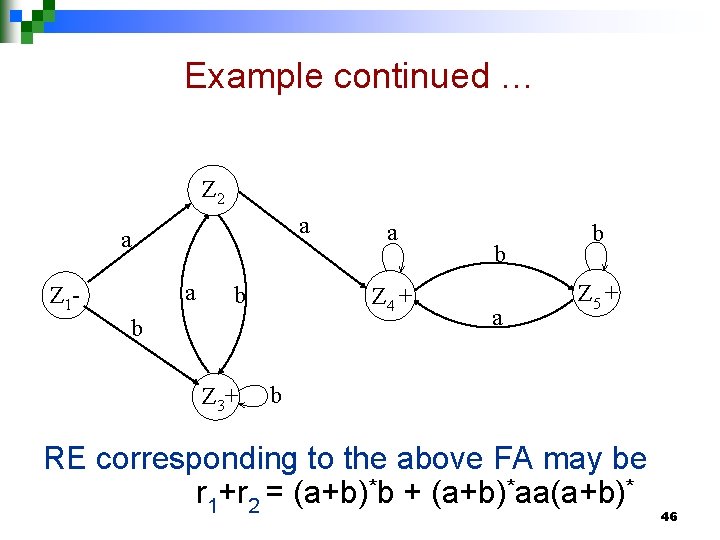
Example continued … Old States z 1–=(x 1, y 1) z 2 =(x 1, y 2) z 3+ =(x 2, y 1) z 4+ =(x 1, y 3) z 5+ =(x 2, y 3) New States after reading a (x 1, y 2) =z 2 (x 1, y 3) =z 4 (x 1, y 2) = z 2 (x 1, y 3) = z 4 b (x 2, y 1) =z 3 (x 2, y 1) = z 3 (x 2, y 3) = z 5 45

Example continued … Z 2 a a a Z 1 - b Z 4 + b Z 3+ a b Z 5 + b RE corresponding to the above FA may be r 1+r 2 = (a+b)*b + (a+b)*aa(a+b)* 46

Kleene’s Theorem Part III Continued … n Method 2 (Concatenation of two FAs): Using the FAs corresponding to r 1 and r 2, an FA can be built, corresponding to r 1 r 2. This method can be developed considering the following examples 47

Example Let r 1=(a+b)*b defines L 1 and FA 1 is a b b – + X 1 X 2 a and r 2 = (a+b )*aa (a+b )* defines L 2 and FA 2 is b a, b a y 2 y 1 b a y 3+ 48

Concatenation of two FAs Cont… 1. 2. 3. Let FA 3 be an FA corresponding to r 1 r 2, then: initial state of FA 3 =initial state of FA 1 final state of FA 3 =final state of FA 2 if final state of FA 1 is entered, then initial state of FA 2 will also be included. 49

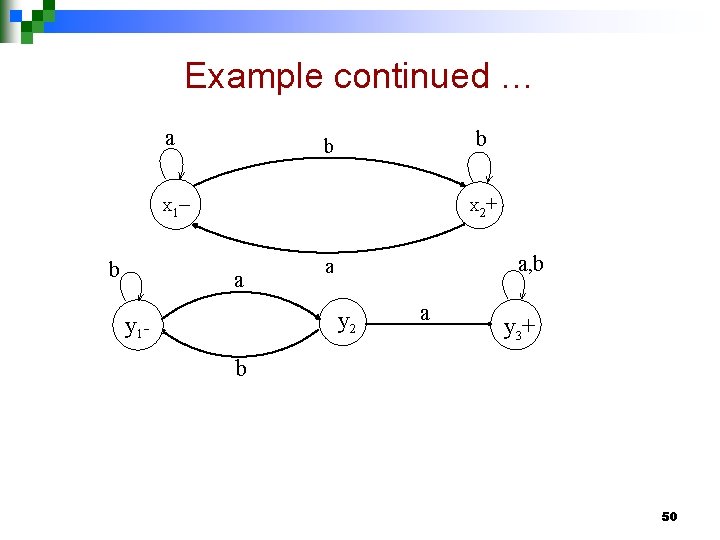
Example continued … a b b – + X 1 b X 2 a a, b a y 2 y 1 - a y 3+ b 50

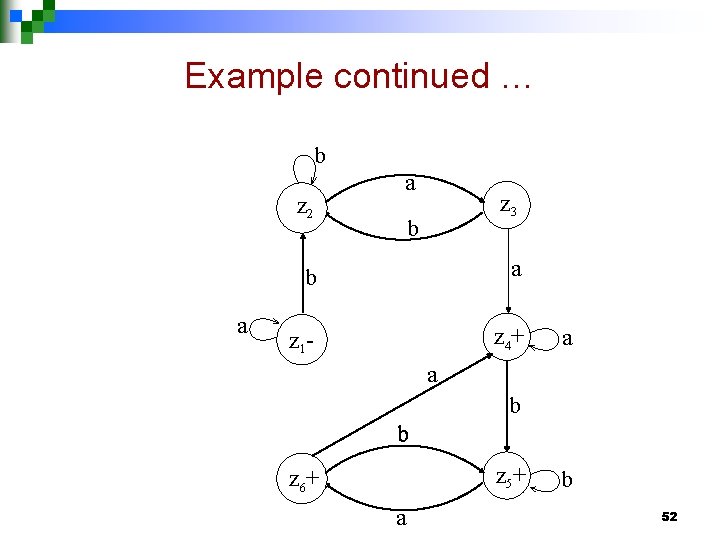
Example continued … Old States New States after reading a b z 1 -=x 1 X 1=z 1 (x 2, y 1)= z 2 Z 2=(x 2, y 1) (x 1, y 2)=z 3 (x 2, y 1)= z 2 Z 3=(x 1, y 2) (x 1, y 3)=z 4 (x 2, y 1)= z 2 z 4+=(x 1, y 3)= z 4 (x 2, y 1, y 3)= z 5+=(x 2, y 1, y 3) (x 1, y 2 , y 3)= z 6 (x 2, y 1, y 3)= z 5 z 6+=(x 1, y 2, y 3) (x 1, y 3)= z 4 (x 2 , y 1, y 3)= z 5 51

Example continued … b z 2 a a z 3 b b a z 1 - z 4+ a a b b z 5+ z 6+ a b 52

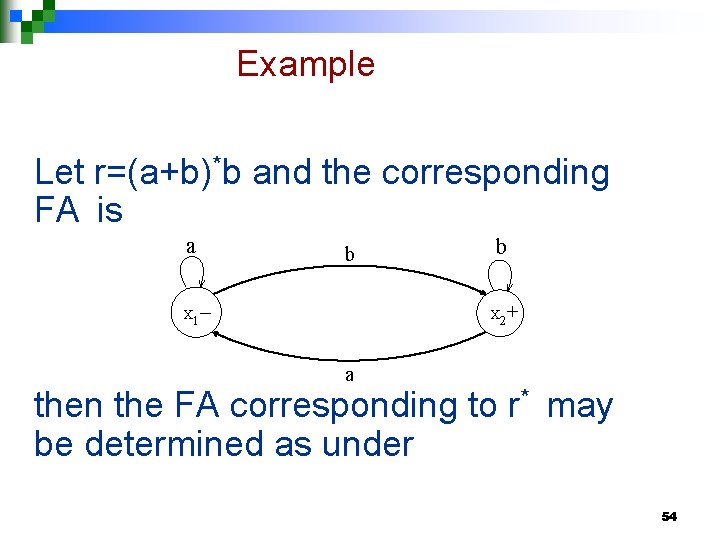
Kleene’s Theorem Part III Continued … n Method 3: (Closure of an FA) Building an FA corresponding to r*, using the FA corresponding to r. Closure of an FA is same as concatenation of an FA with itself, except that the initial state of the required FA is also the final state 53

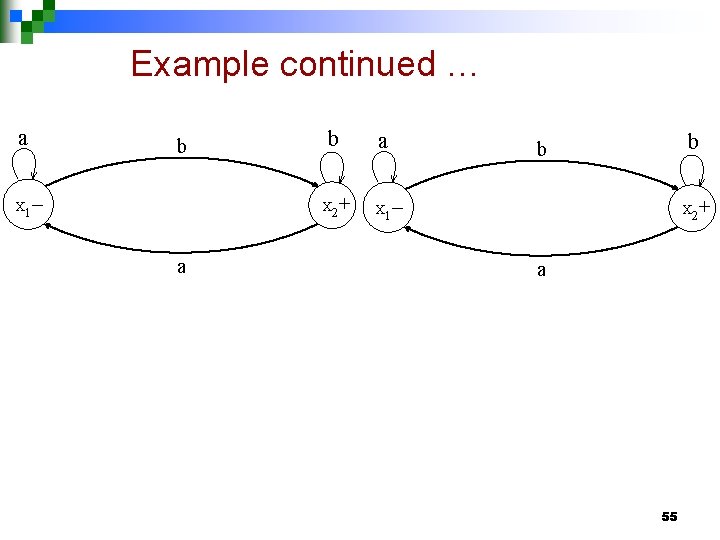
Example Let r=(a+b)*b and the corresponding FA is a b – b + X 1 X 2 a then the FA corresponding to r* may be determined as under 54

Example continued … a b – b + X 1 X 2 a a b b – + X 1 X 2 a 55

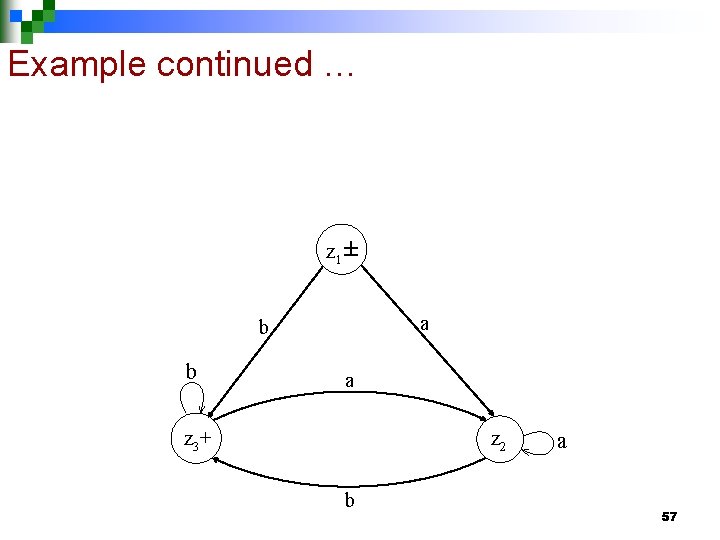
Example continued … Old States New States after reading a b Final z 1 ± = x 1 = z 2 (x 2, x 1) = z 3 Non-final z 2 = x 1 = z 2 (x 2, x 1) = z 3+ = (x 2, x 1) x 1 = z 2 (x 2, x 1) = z 3 The corresponding transition diagram may be as under 56

Example continued … z 1± a b b a z 3+ z 2 b a 57

Thank You! 58