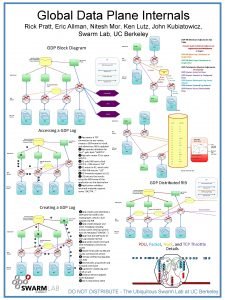
GRAPHTHEORY AND APPLICATIONS Nitesh Tripathi MOTIVATION What is

GRAPH-THEORY AND APPLICATIONS Nitesh Tripathi

MOTIVATION What is the common link between the following problems: ➢ Traffic network design and cancer research? ➢ Arranging marriages and scheduling flights? ➢ Finding cure for mental illness, computer chip design, architectural floor planning, fighting terror online? ➢ Fighting epidemics, e-commerce, designing voting schemes, job assignment, designing electrical networks, deciding on facility location, etc. 2

WHAT IS A GRAPH? ➢ A set of points and lines joining these points. ➢ Formally: G=(V, E), V-vertices, E-edges. v 1 e 6 v 4 v 3 e 2 V 2 and v 3 are adjacent. e 2 is incident with v 2. e 3 e 5 v 2 e 4 v 5 3

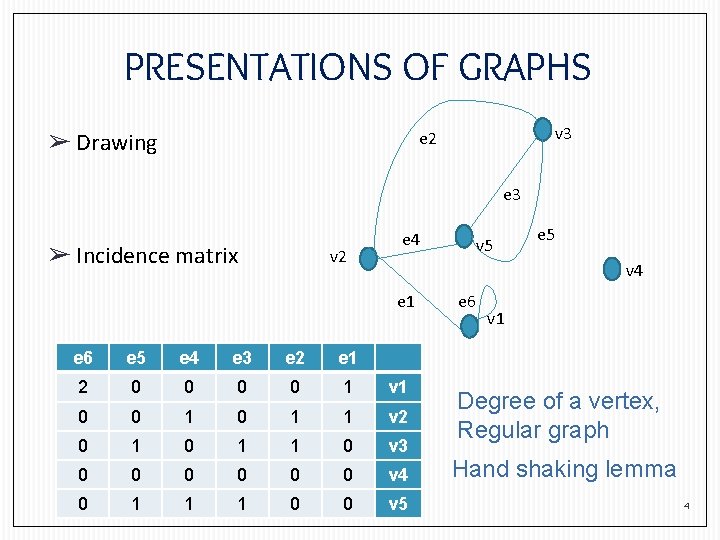
PRESENTATIONS OF GRAPHS ➢ Drawing v 3 e 2 e 3 ➢ Incidence matrix v 2 e 4 v 5 e 5 v 4 e 1 e 6 e 5 e 4 e 3 e 2 e 1 2 0 0 1 v 1 0 0 1 1 v 2 0 1 1 0 v 3 0 0 0 v 4 0 1 1 1 0 0 v 5 e 6 v 1 Degree of a vertex, Regular graph Hand shaking lemma 4

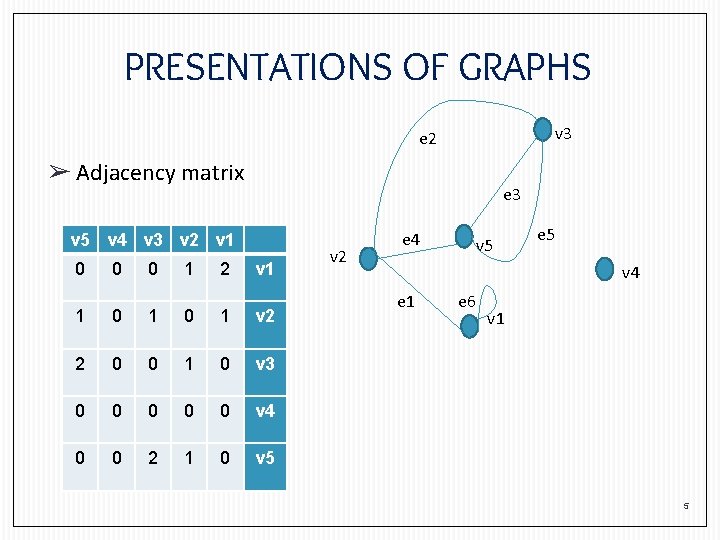
PRESENTATIONS OF GRAPHS v 3 e 2 ➢ Adjacency matrix e 3 v 5 v 4 v 3 v 2 v 1 0 0 0 1 2 v 1 1 0 1 v 2 2 0 0 1 0 v 3 0 0 0 v 4 0 0 2 1 0 v 5 v 2 e 4 v 5 e 5 v 4 e 1 e 6 v 1 5

DIRECTED GRAPHS v 3 e 2 ➢ Adjacency matrix e 3 v 5 v 4 v 3 v 2 v 1 0 0 1 v 2 1 0 0 v 3 0 0 0 v 4 0 0 1 1 0 v 5 v 2 e 4 e 1 v 5 e 6 e 5 v 4 v 1 6

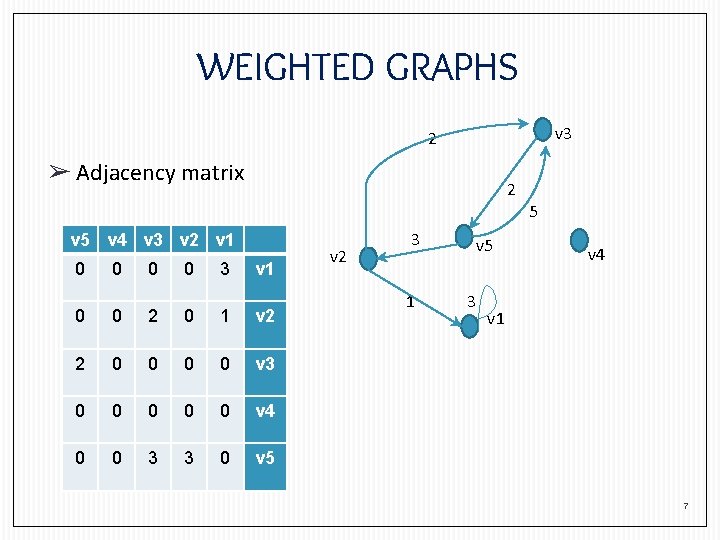
WEIGHTED GRAPHS v 3 2 ➢ Adjacency matrix 2 5 v 4 v 3 v 2 v 1 0 0 3 v 1 0 0 2 0 1 v 2 2 0 0 v 3 0 0 0 v 4 0 0 3 3 0 v 5 v 2 3 1 v 5 3 v 4 v 1 7

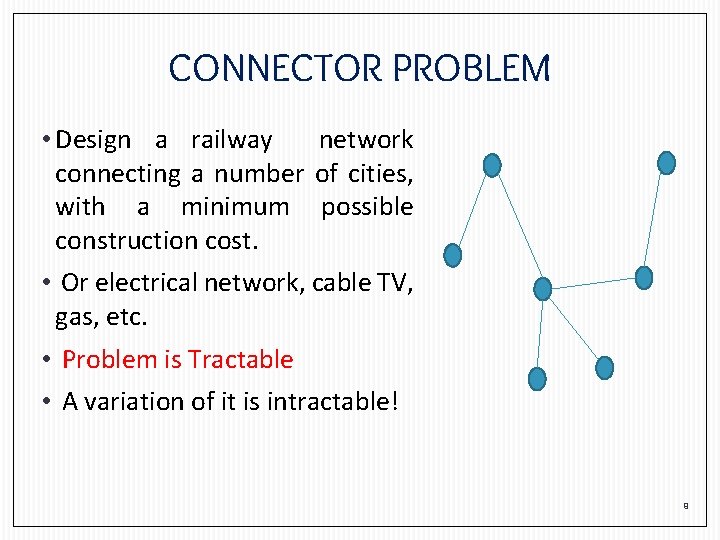
CONNECTOR PROBLEM • Design a railway network connecting a number of cities, with a minimum possible construction cost. • Or electrical network, cable TV, gas, etc. 8

CONNECTOR PROBLEM • Design a railway network connecting a number of cities, with a minimum possible construction cost. • Or electrical network, cable TV, gas, etc. • Problem is Tractable • A variation of it is intractable! 9

CONNECTOR PROBLEM GRAPH-THEORY • Definition: A tree is a connected acyclic graph. • Connected = between any 2 vertices there is a path. • Acyclic = contains no cycles. • Spanning = contains all the vertices in the graph. • Connector problem: Given a weighted graph G: Find a minimum weight spanning tree of G. 10

CONNECTOR PROBLEM GRAPH-THEORY • Computing Minimum Spanning Tree is polynomial time solvable. • Greedy Algorithms: Prim’s and Kruskal’s Algorithm 11

TRAVELLING SALESMAN PROBLEM Wonderla Intractable! Mantri Mall Nandi Hills Iskcon Temple CSA, IISc Orion Mall Summer school students begin at CSA IISc, have to visit all the places exactly once, and return to CSA in a shortest possible distance. (or time, or cost) 12

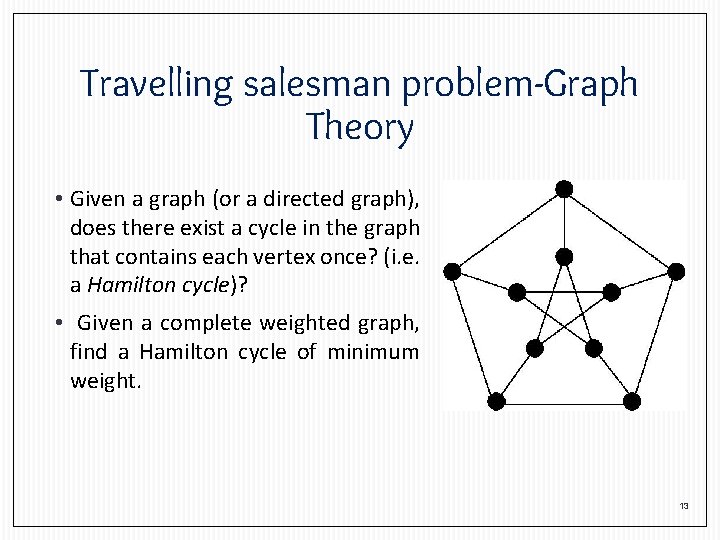
Travelling salesman problem-Graph Theory • Given a graph (or a directed graph), does there exist a cycle in the graph that contains each vertex once? (i. e. a Hamilton cycle)? • Given a complete weighted graph, find a Hamilton cycle of minimum weight. 13

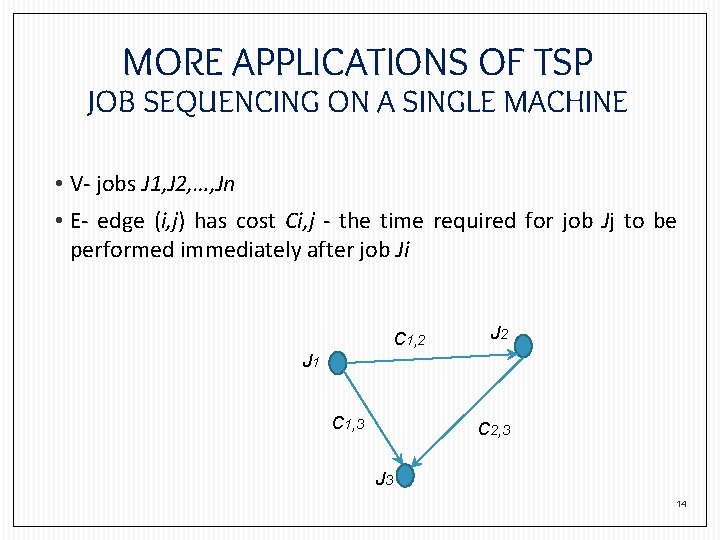
MORE APPLICATIONS OF TSP JOB SEQUENCING ON A SINGLE MACHINE • V- jobs J 1, J 2, …, Jn • E- edge (i, j) has cost Ci, j - the time required for job Jj to be performed immediately after job Ji C 1, 2 J 1 C 1, 3 C 2, 3 J 3 14

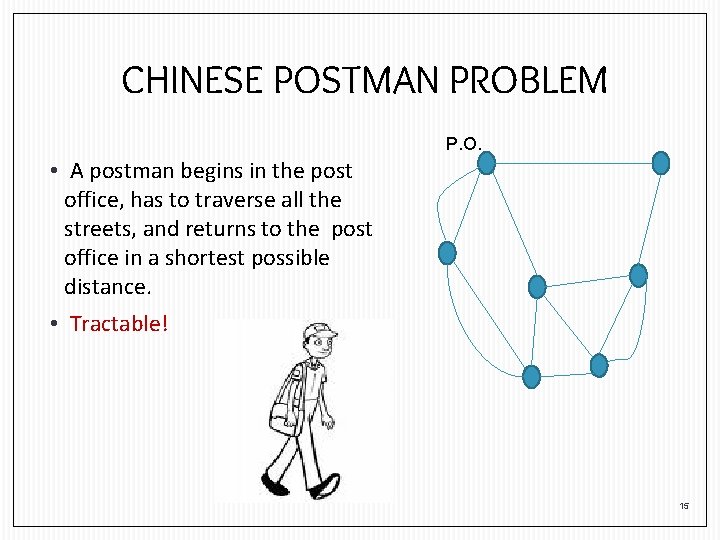
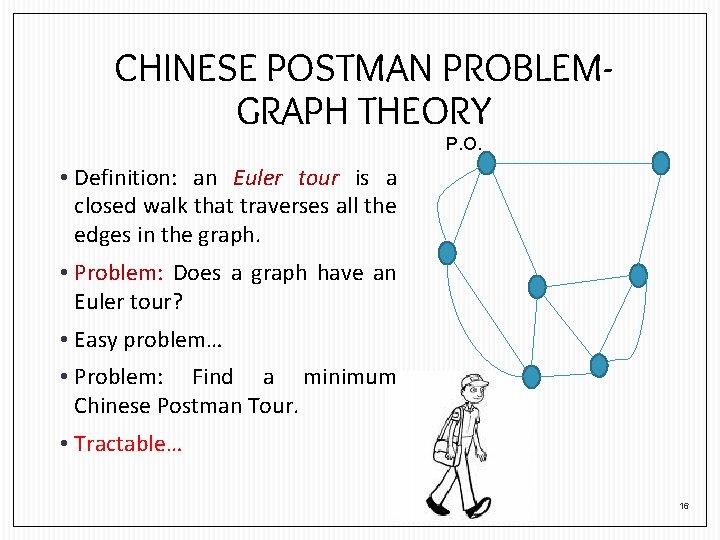
CHINESE POSTMAN PROBLEM P. O. • A postman begins in the post office, has to traverse all the streets, and returns to the post office in a shortest possible distance. • Tractable! 15

CHINESE POSTMAN PROBLEMGRAPH THEORY P. O. • Definition: an Euler tour is a closed walk that traverses all the edges in the graph. • Problem: Does a graph have an Euler tour? • Easy problem… • Problem: Find a minimum Chinese Postman Tour. • Tractable… 16

CHINESE POSTMAN PROBLEMANOTHER APPLICATION Testing a computer program • V – states of a program • E – transitions between the states • Problem: Generate input data that forces the program to test all possible transitions. • Another Problem: Test all pairs of consecutive transitions… (how should we do that? ) 17

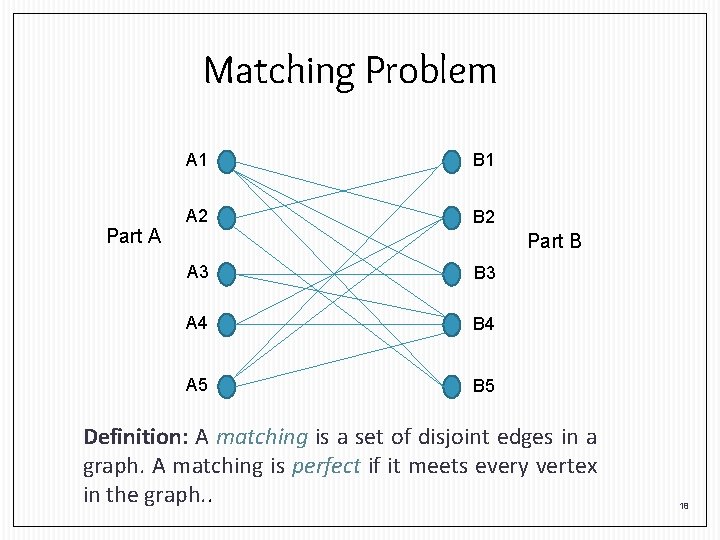
Matching Problem Part A A 1 B 1 A 2 B 2 Part B A 3 B 3 A 4 B 4 A 5 B 5 Definition: A matching is a set of disjoint edges in a graph. A matching is perfect if it meets every vertex in the graph. . 18

Matching Problem A 1 B 1 A 2 B 2 Part A Part B A 3 B 3 A 4 B 4 A 5 B 5 Is this a maximum matching? 19

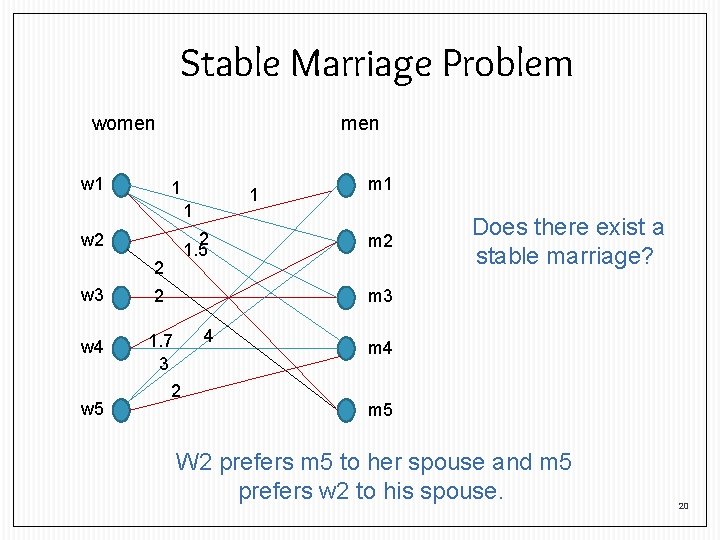
Stable Marriage Problem women w 1 men 1 1 1 2 1. 5 w 2 2 w 3 2 w 4 1. 7 3 w 5 m 1 m 2 Does there exist a stable marriage? m 3 4 2 m 4 m 5 W 2 prefers m 5 to her spouse and m 5 prefers w 2 to his spouse. 20

Assignment Problem machines workers w 1 1 3 1 2 1. 5 w 2 2 w 3 2 w 4 1. 7 3 w 5 m 1 m 2 m 3 2 4 m 5 Find a minimum (maximum) cost assignment of workers to machines 21

Applications • Assigning doctors to hospitals. • Assigning people to jobs. • Assigning students to dormitories. • Assigning pairs of drivers to trucks. • Etc. • Stable Matching Problem can be solved in polynomial time using Gale-Shapley Algorithm. 22

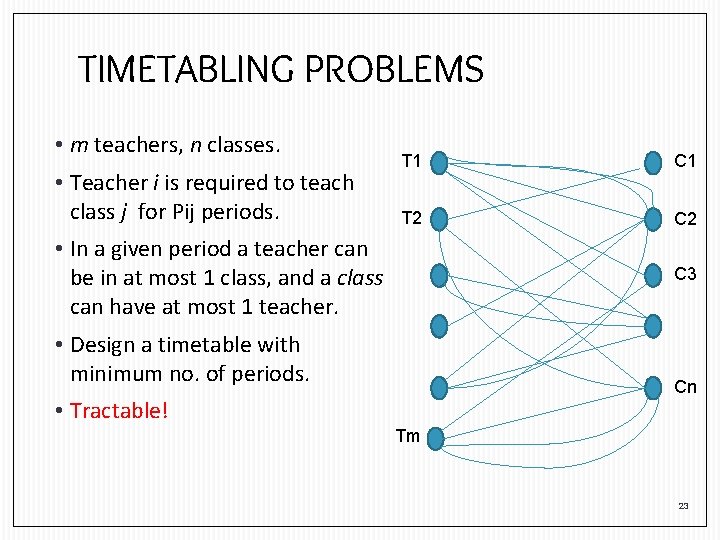
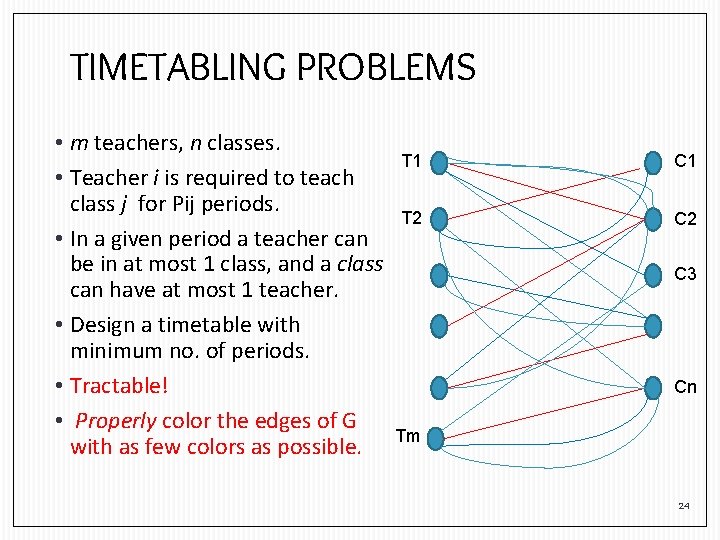
TIMETABLING PROBLEMS • m teachers, n classes. • Teacher i is required to teach class j for Pij periods. T 1 C 1 T 2 C 2 • In a given period a teacher can be in at most 1 class, and a class can have at most 1 teacher. C 3 • Design a timetable with minimum no. of periods. Cn • Tractable! Tm 23

TIMETABLING PROBLEMS • m teachers, n classes. • Teacher i is required to teach class j for Pij periods. • In a given period a teacher can be in at most 1 class, and a class can have at most 1 teacher. • Design a timetable with minimum no. of periods. • Tractable! • Properly color the edges of G with as few colors as possible. T 1 C 1 T 2 C 3 Cn Tm 24

EDGE COLORING OF GRAPHS • Definition: A proper k- edge coloring of a graph G=(V, E) is a mapping • c: E {1, 2, …, k} such that adjacent edges receive distinct colors. • If the maximum degree is Δ then clearly k ≥ Δ • Theorem (Vizing): Any graph has either a Δ-coloring or a (Δ+1)-coloring. • Designing a time-table is a proper edge coloring of a graph. • Theorem A bipartite graph has a Δ-coloring 25

Questions? 26