Graph limit theory an overview Lszl Lovsz Etvs

Graph limit theory: an overview László Lovász Eötvös Loránd University, Budapest IAS, Princeton June 2011 1

Limit theories of discrete structures rational numbers trees Aldous, Elek-Tardos graphs digraphs Diaconis-Janson hypergraphs Elek-Szegedy permutations Kohayakawa posets Janson abelian groups Szegedy metric spaces Gromov Elek June 2011 2

Common elements in limit theories sampling trees sampling distance graphs limiting sample distributions digraphs combined limiting sample distributions hypergraphs permutations limit object posets overlay distance abelian groups regularity lemma metric spaces June 2011 applications 3

Limit theories for graphs Dense graphs: Borgs-Chayes-L-Sós-Vesztergombi L-Szegedy Inbetween: distances Bollobás-Riordan regularity lemma Kohayakawa-Rödl, Scott Laplacian Chung Bounded degree graphs: Benjamini-Schramm, Elek June 2011 4

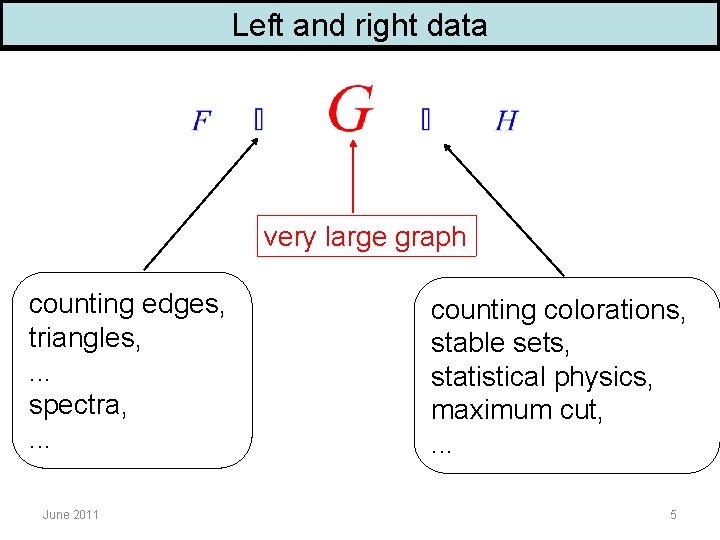
Left and right data very large graph counting edges, triangles, . . . spectra, . . . June 2011 counting colorations, stable sets, statistical physics, maximum cut, . . . 5

Dense graphs: convergence t(F, G): Probability that random map V(F) V(G) preserves edges (G 1, G 2, …) convergent: F t(F, Gn) is convergent June 2011 6

Dense graphs: limit objects W 0 = {W: [0, 1]2 [0, 1], symmetric, measurable} "graphon" Gn W : F: t(F, Gn) t(F, W) June 2011 7

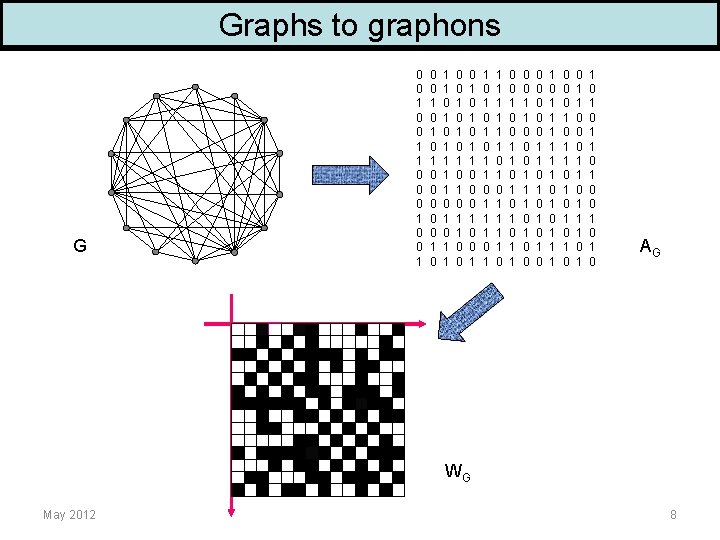
Graphs to graphons G 0 0 1 1 0 0 0 1 0 1 0 0 0 1 0 1 1 1 1 0 0 1 0 1 0 1 1 0 0 0 1 1 0 1 0 1 1 1 1 0 0 0 1 1 0 1 0 1 1 0 0 0 1 1 1 0 0 0 0 1 1 0 1 0 1 0 1 1 1 0 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 0 0 1 0 AG WG May 2012 8

Dense graphs: basic facts For every convergent graph sequence (Gn) there is a W W 0 such that Gn W. Is this the only useful Conversely, W (Gn) such that Gn W. notion of convergence dense graphs? W is essentially of unique (up to measure-preserving transformation). June 2011 9

Bounded degree: convergence Local : neighborhood sampling Benjamini-Schramm Global : metric space Gromov Local-global : Hatami-L-Szegedy Right-convergence, … Borgs-Chayes-Gamarnik June 2011 10

Graphings Graphing: bounded degree graph G on [0, 1] such that: E(G) is a Borel set in [0, 1]2 measure preserving: 0 A B 1 deg. B(x)=2 June 2011 11

Graphings Every Borel subgraph of a graphing is a graphing. Every graph you ever want to construct from a graphing is a graphing D=1: graphing measure preserving involution G is a graphing G=G 1 … Gk measure preserving involutions (k 2 D-1) June 2011 12

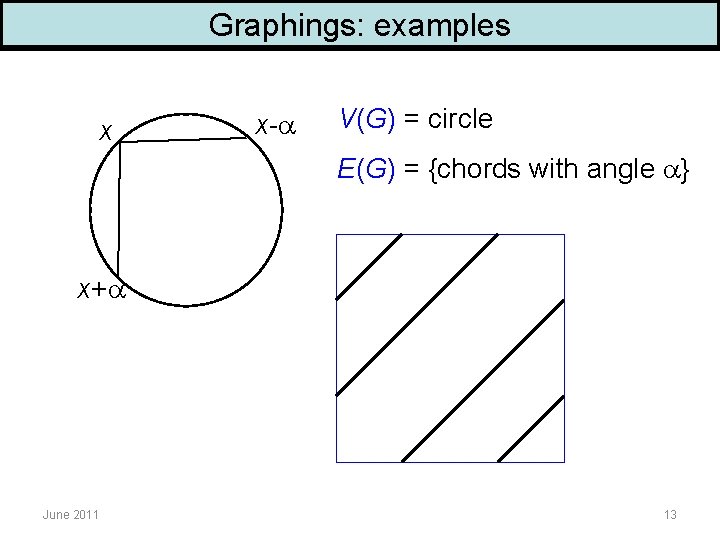
Graphings: examples x x- V(G) = circle E(G) = {chords with angle } x+ June 2011 13

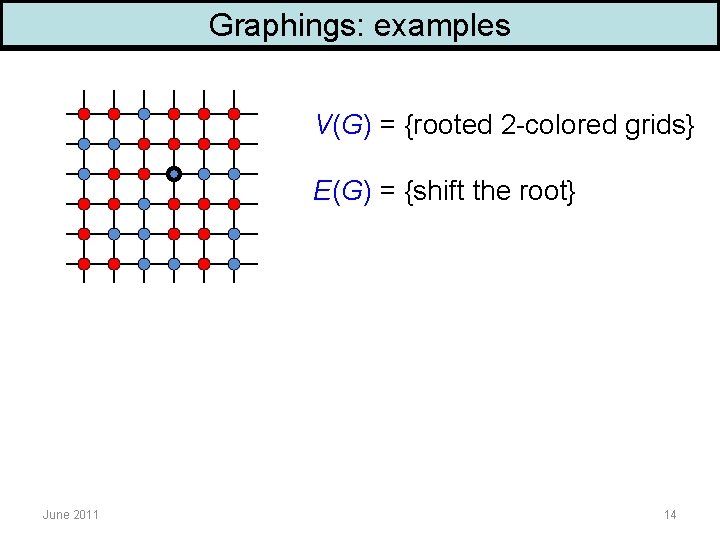
Graphings: examples V(G) = {rooted 2 -colored grids} E(G) = {shift the root} June 2011 14

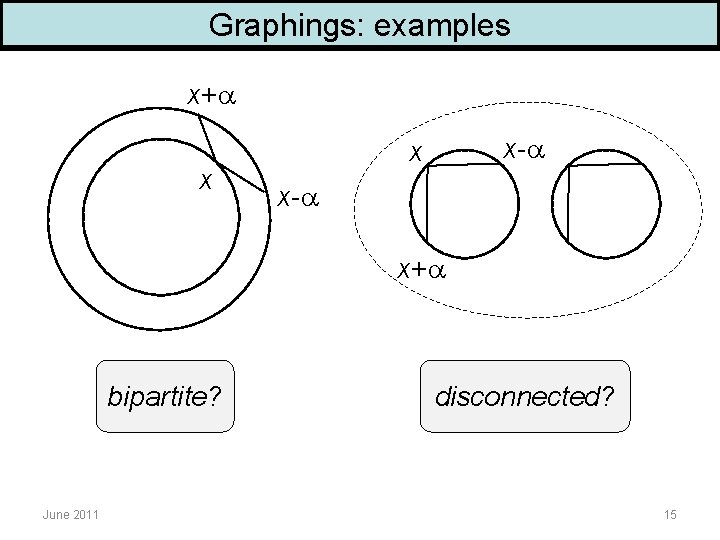
Graphings: examples x+ x x- x+ bipartite? June 2011 disconnected? 15

Graphings and involution-invariant distributions x: random point of [0, 1] Gx: connected component of G containing x Gx is a random connected graph with bounded degree This distribution is "invariant" under shifting the root. Every involution-invariant distribution can be represented by a graphing. Elek June 2011 16

Graph limits and involution-invariant distributions graphs, graphings, or inv-inv distributions (Gn) locally convergent: Cauchy in d Gn G: d (Gn, G) 0 (n ) inv-inv distribution June 2011 17

Graph limits and involution-invariant distributions Every locally convergent sequence of bounded-degree graphs has a limiting inv-inv distribution. Benjamini-Schramm Is every inv-inv distribution the limit of a locally convergent graph sequence? Aldous-Lyons June 2011 18

Local-global convergence (Gn) locally-globally convergent: Cauchy in d k Gn G: dk(Gn, G) 0 (n ) graphing June 2011 19

Local-global graph limits Every locally-globally convergent sequence of bounded-degree graphs has a limit graphing. Hatami-L-Szegedy June 2011 20

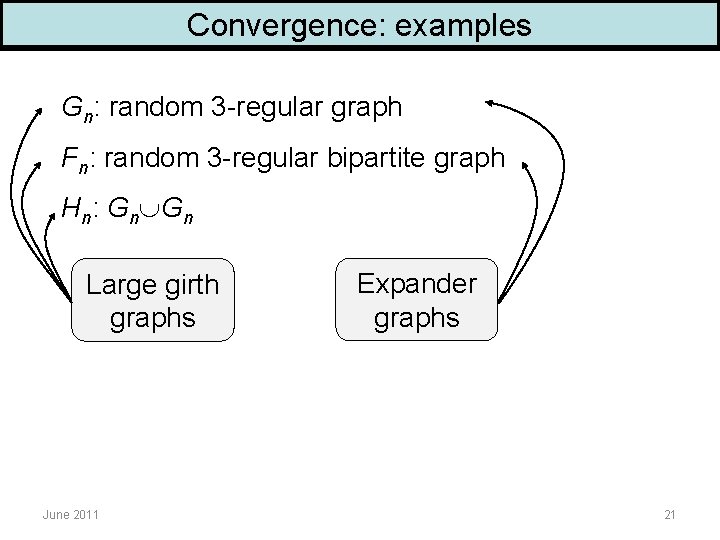
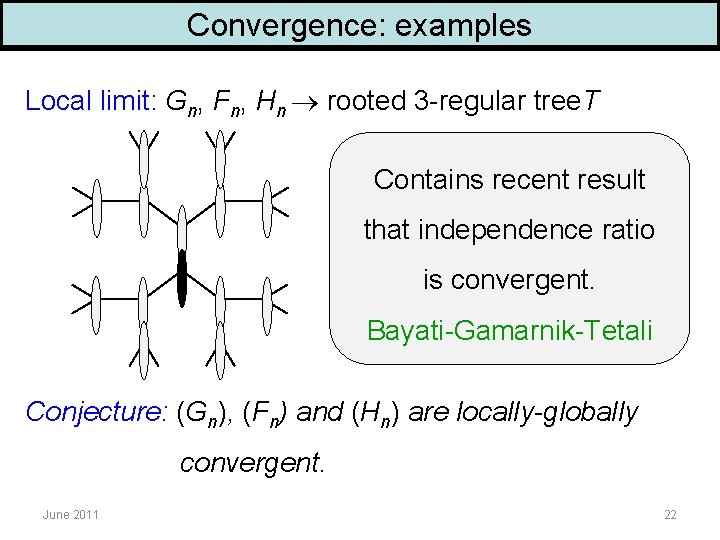
Convergence: examples Gn: random 3 -regular graph Fn: random 3 -regular bipartite graph Hn: Gn Gn Large girth graphs June 2011 Expander graphs 21

Convergence: examples Local limit: Gn, Fn, Hn rooted 3 -regular tree. T Contains recent result that independence ratio is convergent. Bayati-Gamarnik-Tetali Conjecture: (Gn), (Fn) and (Hn) are locally-globally convergent. June 2011 22

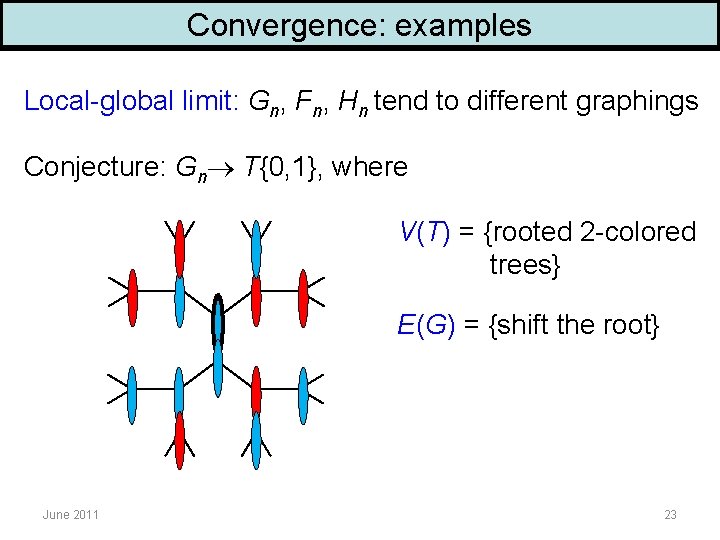
Convergence: examples Local-global limit: Gn, Fn, Hn tend to different graphings Conjecture: Gn T{0, 1}, where V(T) = {rooted 2 -colored trees} E(G) = {shift the root} June 2011 23

Local-global convergence: dense case Every convergent sequence of graphs is Cauchy in dk L-Vesztergombi June 2011 24

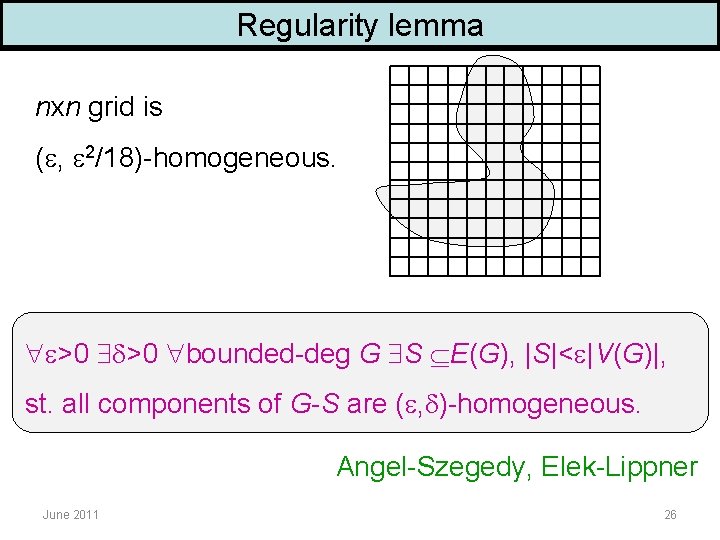
Regularity lemma Given an arbitrarily large graph G and an >0, decompose G into f( ) "homogeneous" parts. ( , )-homogeneous graph: S E(G), |S|< |V(G)|, all connected components of G-S with > |V(G)| nodes have the same neighborhood distribution (up to ). June 2011 25

Regularity lemma nxn grid is ( , 2/18)-homogeneous. >0 bounded-deg G S E(G), |S|< |V(G)|, st. all components of G-S are ( , )-homogeneous. Angel-Szegedy, Elek-Lippner June 2011 26

Regularity lemma Given an arbitrarily large graph G and an >0, find a graph H of size at most f( ) such that G and H are -close in sampling distance. Frieze-Kannan "Weak" Regularity Lemma suffices in the dense case. f( ) exists in the bounded degree case. Alon June 2011 27

Extremal graph theory It is undecidable whether Hatami-Norin holds for every graph G. It is undecidable whethere is a graphing with almost all r-neighborhoods in a given family F. Csóka June 2011 28

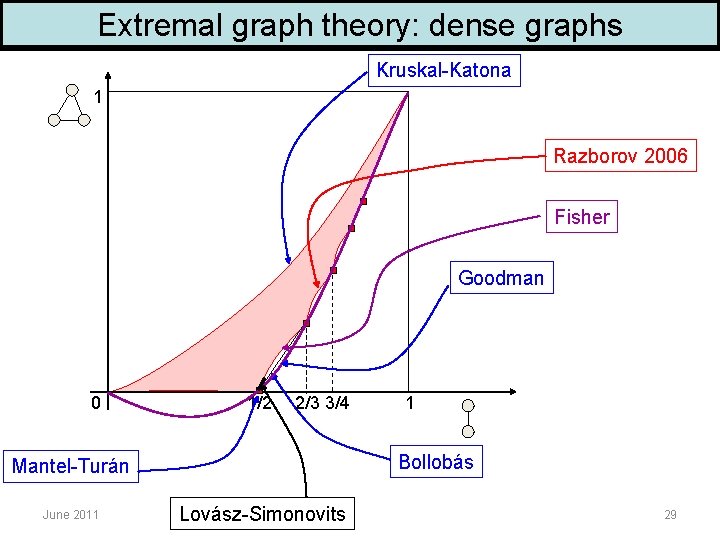
Extremal graph theory: dense graphs Kruskal-Katona 1 Razborov 2006 Fisher Goodman 0 1/2 2/3 3/4 Bollobás Mantel-Turán June 2011 1 Lovász-Simonovits 29

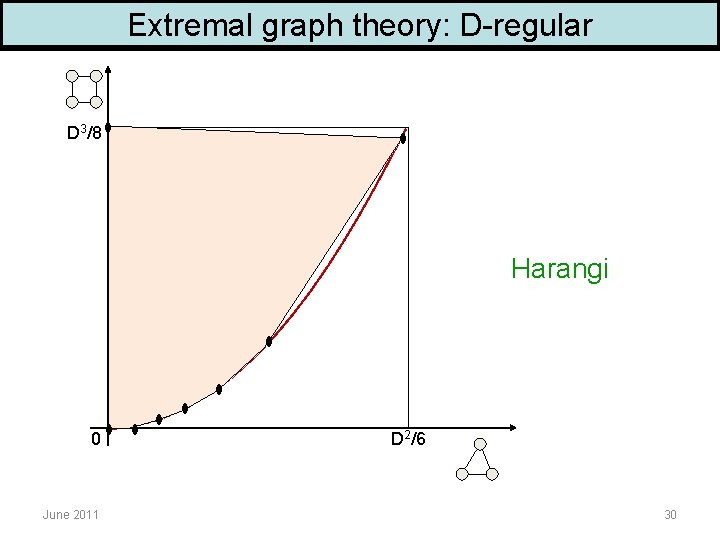
Extremal graph theory: D-regular D 3/8 Harangi 0 June 2011 D 2/6 30