9 3 Geometric Sequences Series Geometric Sequence The









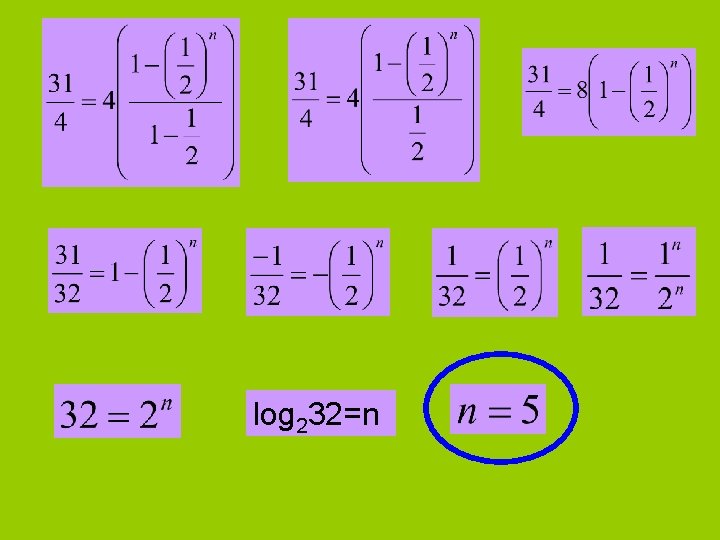





- Slides: 15

9 -3 Geometric Sequences & Series

Geometric Sequence • The ratio of a term to it’s previous term is constant. • This means you multiply by the same number to get each term. • This number that you multiply by is called the common ratio (r).

Example: Decide whether each sequence is geometric. • 4, -8, 16, -32, … • -8/ =-2 4 • 16/ =-2 -8 • -32/ =-2 16 • Geometric (common ratio is -2) • 3, 9, -27, -81, 243, … • 9/ =3 3 • -27/ =-3 9 • -81/ =3 -27 • 243/ =-3 -81 • Not geometric

Find the rule for an for the following sequence. • 2, 4, 8, 16, 32… 1 st, 2 nd, 3 rd, 4 th, 5 th Think of how to use the common ratio, n and a 1, the term value. to determine

Rule for a Geometric Sequence n-1 an=a 1 r Example 1: Write a rule for the nth term of the sequence 5, 20, 80, 320, …. Then find a 8. • First, find r. a 8=5(4)8 -1 • r= 20/5 = 4 a 8=5(4)7 • an=5(4)n-1 a 8=5(16, 384) A 8=81, 920

Example 2: One term of a geometric sequence is a 4=3. The common ratio is r=3. Write a rule for the nth term. • Use an=a 1 rn-1 3=a 1(3)4 -1 3=a 1(3)3 3=a 1(27) 1/ =a 9 1 • an=a 1 rn-1 an=(1/9)(3)n-1

Ex 3: Two terms of a geometric sequence are a 2=-4 and a 6=-1024. Write a rule for the nth term. • Write 2 equations, one for each given term. a 2=a 1 r 2 -1 OR -4=a 1 r a 6=a 1 r 6 -1 OR -1024=a 1 r 5 • Use these 2 equations & substitution to solve for a 1 & r. -4/ =a If r=4, then a 1=-1. r 1 -1024=(-4/r)r 5 an=(-1)(4)n-1 If r=-4, then a 1=1. 4 -1024=-4 r n-1 a =(1)(-4) 4 n 256=r Both n-1 a =(-4) 4=r & -4=r n Work!

Formula for the Sum of a Finite Geometric Series n = # of terms a 1 = 1 st term r = common ratio

Example 4: Consider the geometric series 4+2+1+½+…. • Find the sum of the first 10 terms. • Find n such that Sn=31/4.
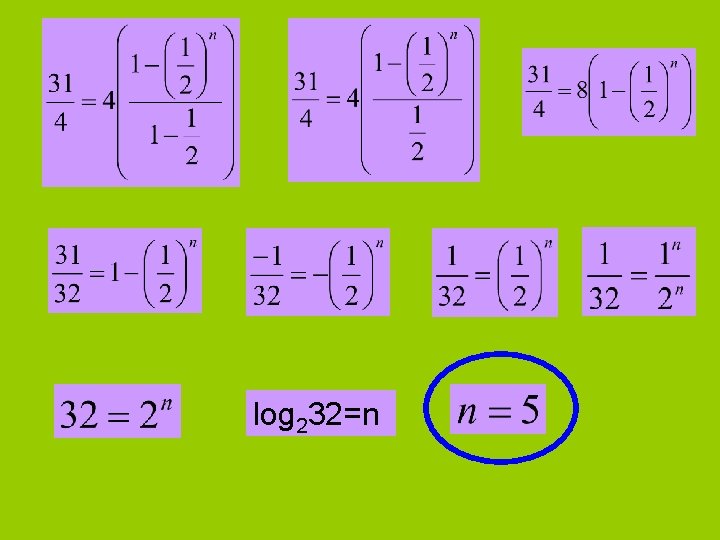
log 232=n

Looking at infinite series, what happens to the sum as n approaches infinity in each case? 3 + 9 + 27 + 81, +…. + 3 n 27 + 9 + 3, + 1/3 + …. + (1/3)n Notice, if the sum does not exist. and thus

So what if Looking at infinite series, what happens to the sum as n approaches infinity if ?

Sum of a Infinite Geometric Series when n = # of terms a 1 = 1 st term r = common ratio

Ex 5: Find the Sum of the infinite series a) 1 + 1. 5 + 2. 25 + 3. 375 + … Sum DNE since r = 1. 5 and is > 1 b) 9 + 6 + 4 + 8/3 + … r = 2/3 and is < 1 so we use the formula

H Dub 9 -3 Pg. 669 #3 -42 (3 n), 53 -55, 73 -75, 79 -81
 Arithmetic and geometric sequences and series
Arithmetic and geometric sequences and series 10-3 geometric sequences and series
10-3 geometric sequences and series 10-3 geometric sequences and series
10-3 geometric sequences and series 10-3 geometric sequences and series
10-3 geometric sequences and series Sum of infinite series
Sum of infinite series Geometric sequence formula
Geometric sequence formula Recursive formula geometric
Recursive formula geometric 9-1 geometric sequences
9-1 geometric sequences Lesson 3: arithmetic and geometric sequences
Lesson 3: arithmetic and geometric sequences Recursive geometric formula
Recursive geometric formula Geometric sequences
Geometric sequences Geometric and arithmetic sequences formulas
Geometric and arithmetic sequences formulas 9-3 geometric sequences
9-3 geometric sequences Geometric sequences formula
Geometric sequences formula Exponential function geometric sequences
Exponential function geometric sequences Financial maths formulas
Financial maths formulas