Numerical methods to solve parabolic PDEs Mathematical models

Numerical methods to solve parabolic PDEs

Mathematical models: 5° Classification based on the type of the solution (except, usually, the empirical models) 1. ANALYTICAL SOLUTIONS MATHEMATICAL ANALYSIS ALGEBRA 2. NUMERICAL SOLUTIONS NUMERICAL COMPUTATION Ex. : numerical methods for PDE 1. FINITE DIFFERENCE METHOD (FDM) 2. FINITE ELEMENT METHOD (FEM) 3. METHODS OF LOCATION

Partial differential equation (PDE) Second order Partial differential equation: where u=f(x, y, t), a function that satisfies this equation and that is at least two times differentiable, is said to be a solution of the equation. To obtain a unique solution, it is necessary supply some additional information, namely initial (IC) and boundary (BC) conditions. BC must to be of the order N-1 if N is the order of the equation.

Partial differential equation (PDE) Classical classification for 2 nd order PDE’s if = b 2 - 4 ac < 0 : Elliptic = 0 : Parabolic > 0 : Hyperbolic

Partial differential equation (PDE) Classical classification for 2 nd order PDE’s a=1, b=0, c=1 Laplace’s equation = b 2 - 4 ac = -4 for heat conduction Heat conduction equation is elliptic.

Partial differential equation (PDE) Classical classification for 2 nd order PDE’s a=D, b=0, c=0 Molar Diffusion = b 2 - 4 ac = 02 - 4 D 0 = 0 Diffusion equation is parabolic.

Partial differential equation (PDE) Classical classification for 2 nd order PDE’s Convection in conservation laws First order / t or / h a=1, b=v, c=0 = b 2 - 4 ac = v 2 a=v, b=1, c=0 = b 2 - 4 ac = 1 Convection equation is hyperbolic

Second order Partial differential equation Classification: Type Equation Description Parabolic Unsteady-state problem in which transport by conduction or diffusion is important Elliptic Steady-state problem in which transport by conduction or diffusion is important Hyperbolic Unsteady-state problem in which transport by convention phenomenon is important Note: An equation can belong to a class in a certain field another in a different field

Parabolic PDE’s Parabolic (or diffusion) PDE with one spatial independent variable 2° order PDE 2 independent variables Linear with constant coefficients is a diffusion coefficient t Є [0, +∞] x Є [x. A, x. B] I. C. : u(t=0, x)=u*(x) all x B. C. 1: u(t, x=x. A)=u. A(t) all t (simple case) B. C. 2: u(t, x=x. B)=u. B(t) all t (simple case) Analytical solution: u=u(t, x) where u is a continuous function of t and x

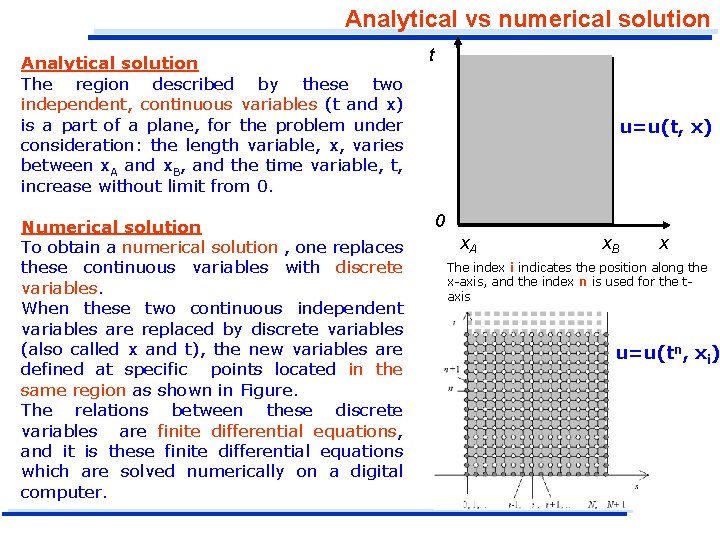
Analytical vs numerical solution Analytical solution The region described by these two independent, continuous variables (t and x) is a part of a plane, for the problem under consideration: the length variable, x, varies between x. A and x. B, and the time variable, t, increase without limit from 0. Numerical solution To obtain a numerical solution , one replaces these continuous variables with discrete variables. When these two continuous independent variables are replaced by discrete variables (also called x and t), the new variables are defined at specific points located in the same region as shown in Figure. The relations between these discrete variables are finite differential equations, and it is these finite differential equations which are solved numerically on a digital computer. t u=u(t, x) 0 x. A x. B x The index i indicates the position along the x-axis, and the index n is used for the taxis u=u(tn, xi)

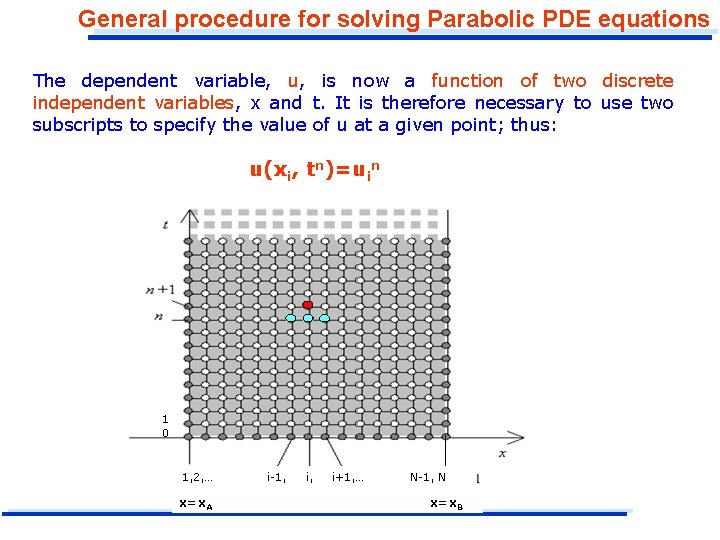
General procedure for solving Parabolic PDE equations The dependent variable, u, is now a function of two discrete independent variables, x and t. It is therefore necessary to use two subscripts to specify the value of u at a given point; thus: u(xi, tn)=uin 1 0 1, 2, … x=x. A i-1, i+1, … N-1, N x=x. B

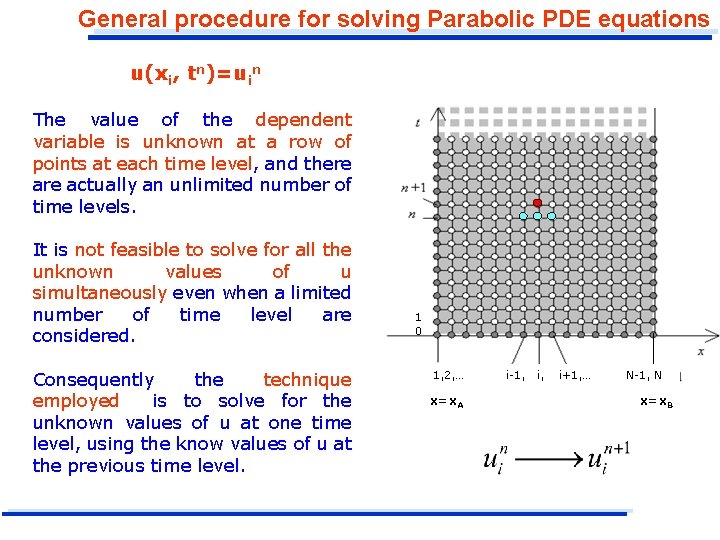
General procedure for solving Parabolic PDE equations u(xi, tn)=uin The value of the dependent variable is unknown at a row of points at each time level, and there actually an unlimited number of time levels. It is not feasible to solve for all the unknown values of u simultaneously even when a limited number of time level are considered. Consequently the technique employed is to solve for the unknown values of u at one time level, using the know values of u at the previous time level. 1 0 1, 2, … x=x. A i-1, i+1, … N-1, N x=x. B

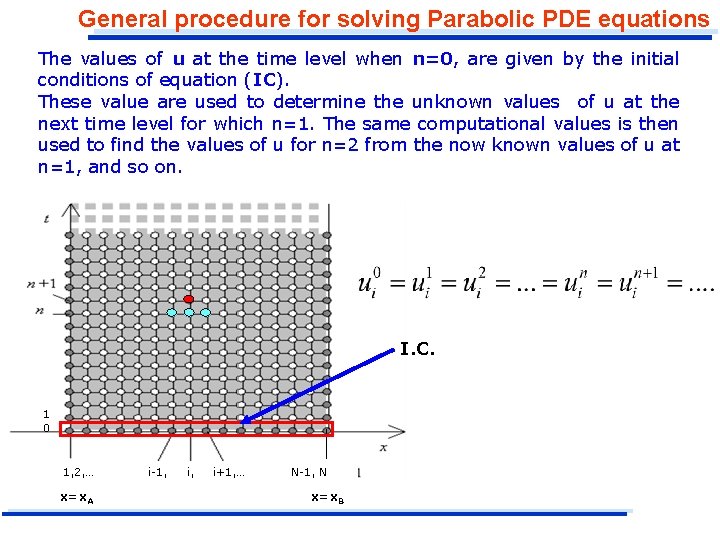
General procedure for solving Parabolic PDE equations The values of u at the time level when n=0, are given by the initial conditions of equation (IC). These value are used to determine the unknown values of u at the next time level for which n=1. The same computational values is then used to find the values of u for n=2 from the now known values of u at n=1, and so on. I. C. 1 0 1, 2, … x=x. A i-1, i+1, … N-1, N x=x. B

General procedure for solving Parabolic PDE equations This procedure is continued for as many time increments as desired. Therefore, the finite difference equations are formulated so that they contain values of u at two consecutive levels. The index n is used to designate the last time level at which the value of u are known, and the index n+1 is used to designate the next time level at which variables of the dependent variable are unknown. t (i-1, n+1)(i+1, n+1) unknown value unless it is given by a boundary condition. n+1 n (i, n) i-1 i i+1 x known value

Finite Difference Methods The finite difference method (FDM) was first developed by A. Thom* in the 1920 s under the title “The method of square” to solve nonlinear hydrodynamic equations. *A. Thom and C. J. Apelt, Field Computations in Engineering and Physics. London: D. Van Nostrand, 1961. “The finite difference techniques are based upon the approximations that permit replacing differential equations by finite difference equations. These finite difference approximations are algebraic in form, and the solutions are related to grid points”.

Finite Difference Methods Thus, a finite difference solution basically involves three steps: 1. Dividing the solution into grids of nodes 2. Approximating the given differential equation by finite difference equivalence that relates the solutions to grid points (In finite difference methods, each derivative of the PDE is replaced by an equivalent finite difference approximation) 3. Solving the finite difference equations subject to the prescribed boundary conditions and/or initial conditions

Finite Difference Methods If x. A=0 and x. B=L, the region between 0 and L along the x-axis is divided into N equal increment of size x, whit grid points being placed on each boundary. The time-axis is divided into increments of size t. t tn=n*Dt (i-1, n+1)(i+1, n+1) xi=x. A+i*Dx=i*Dx n+1 n (i, n) x i i+1 0 i-1 L Some useful relations between values of the independent variable at adjacent points: xi+1=xi+i* x xi-1=xi-i* x For many numerical solutions, it will be desirable to increase the size of the time step, t, as the solutions progresses.

Finite Difference Methods t (i-1, n+1)(i+1, n+1) n+1 n (i, n) i-1 i i+1 x Both sides must to be evaluated at the same conditions (xi and tn) We will indicate: Evaluate at time tn Evaluate at length xi All i and n The FDM write both sides and check the equality for each grid points

Finite Difference Methods The basis of a finite difference method is the Taylor series expansion of a function. • Consider a continuous function f(x). Its value at neighboring points can be expressed in terms of a Taylor series as: (1) f(xi+ ∆x) =f(xi) +(df/dx)xi (∆x) + (d 2 f/dx 2)xi (∆x 2)/ 2! +. . +(dnf/dxn)xi (∆xn)/n! +…. • The above series converges if ∆x is small and f(x) is differentiable • For a converging series, successive terms are progressively smaller

Finite Difference Methods The terms in the Taylor series expansion can be rearranged to give (df/dx)xi =[f(xi+ ∆x) -f(xi)] /∆x-(d 2 f/dx 2)xi (∆x)/2! -…-(dnf/dxn)xi (∆xn-1)/n! -. . . Or (2) (df/dx)xi ≈[f(xi+ ∆x) -f(xi)] /∆x+O(∆x) • Here O(∆x) implies that the leading term in the neglected terms are of the order of ∆x, i. e. , the error in the approximation reduces by a factor of 2 if ∆x is halved. • Equation (2) is therefore a first approximation for the first derivative. order-accurate

Finite Difference Methods Other Approximations for a First Derivative Other approximations are also possible. Writing the Taylor series expansion for f(xi- ∆x), we have (3) f(xi-∆x) =f(xi) – (df/dx)xi (∆x) +(d 2 f/dx 2)xi (∆x 2)/ 2! -. . +(dnf/dxn)xi (∆xn)/n! + • Equation (3) can approximation : be rearranged to give another first order (4) (df/dx)xi ≈[f(xi) -f(xi-∆x)] /∆x+O(∆x) • Subtracting (3) from (1) gives a second order approximation for df/dx: (5) (df/dx)xi ≈[f(xi+ ∆x) -f(xi-∆x)] /(2∆x) +O(∆x 2)

Finite Difference Methods In summary: • Forward-difference formula (first order-accurate approximation): (df/dx)xi ≈[f(xi+ ∆x) -f(xi)] /∆x+O(∆x) • Backward-difference approximation): formula (first order-accurate (df/dx)xi ≈[f(xi) -f(xi-∆x)] /∆x+O(∆x) • Central-difference formula (second order-accurate approximation): (df/dx)xi ≈[f(xi+ ∆x) -f(xi-∆x)] /(2∆x) +O(∆x 2)

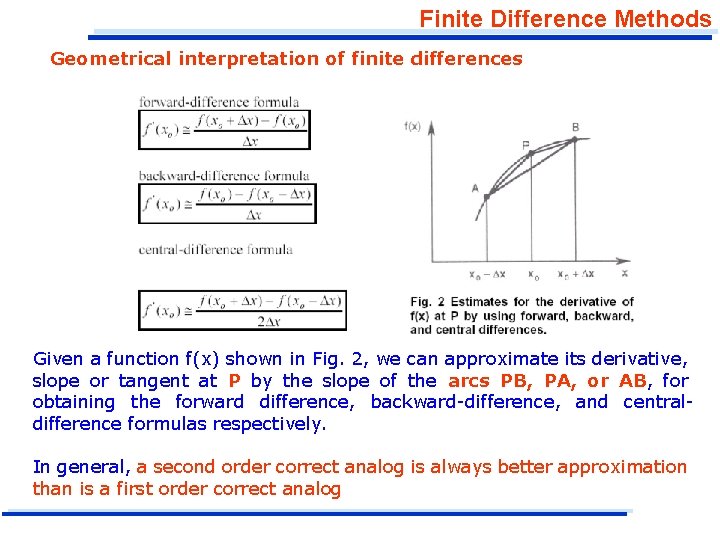
Finite Difference Methods Geometrical interpretation of finite differences Given a function f(x) shown in Fig. 2, we can approximate its derivative, slope or tangent at P by the slope of the arcs PB, PA, or AB, for obtaining the forward difference, backward-difference, and centraldifference formulas respectively. In general, a second order correct analog is always better approximation than is a first order correct analog

Finite Difference Methods Higher derivates Upon adding (1) and (3) (1) f(xi+ ∆x) =f(xi) +(df/dx)xi (∆x) + (d 2 f/dx 2)xi (∆x 2)/ 2! +. . +(dnf/dxn)xi (∆xn)/n! +…. (3) f(xi-∆x) =f(xi) – (df/dx)xi (∆x) +(d 2 f/dx 2)xi (∆x 2)/ 2! -. . +(dnf/dxn)xi (∆xn)/n! + we obtain: f(xi+ ∆x) - f(xi-∆x) =2 f(xi) + (d 2 f/dx 2)xi (∆x 2)/ 2! +O(∆x 4) and we have: (d 2 f/dx 2)xi ≈[f(xi+ ∆x) - 2 f(xi) + f(xi-∆x)] /(∆x 2) +O(∆x 2) (second order-accurate approximation) Higher order finite difference approximations can be obtained by taking more terms in Taylor series expansion.

Type of Errors 1)Discretization or truncation error: εi=yi-y(xi) The discretization error encountered in integrating a differential equation across one step is sometimes called local truncation error. This error is determined solely by the particular numerical solution procedure selected, that is, by the nature of the approximations present in the method; this type of error is independent of computing equipment characteristics. Example: when one replace the first derivate by the finite Forward-difference formula, the truncation error is of the order x, while it is of the order x 2 when a Central-difference formula is used.

Finite Difference Methods Example: • Forward-difference formula (the truncation error is of the order of Dx): (df/dx)xi ≈[f(xi+ ∆x) -f(xi)] /∆x+O(∆x) • Backward-difference formula (the truncation error is of the order of Dx): (df/dx)xi ≈[f(xi) -f(xi-∆x)] /∆x+O(∆x) • Central-difference formula (the truncation error is of the order of Dx 2): (df/dx)xi ≈[f(xi+ ∆x) -f(xi-∆x)] /(2∆x) +O(∆x 2)

Type of Errors 2)The round-off error is determined, for any particular method, by the computing characteristics of the machine which does the calculations due to its finite memory which lead to a an approximation of any irrational number by a “rounded” value.

Type of Errors Reducing the mesh size could increase accuracy, but the mesh size could not be infinitesimal. Decreasing the truncation error by using a finer mesh may result in increasing the roundoff error due to the increased number of arithmetic operations. A point is reached where minimum total error occurs for any particular algorithm using any given word length.

Finite Difference Methods Analog finite difference equation for each total derivates • Forward-difference formula (first order-accurate approximation): (df/dx)xi ≈[f(xi+ ∆x) -f(xi)] /∆x+O(∆x) • Backward-difference approximation): formula (first order-accurate (df/dx)xi ≈[f(xi) -f(xi-∆x)] /∆x+O(∆x) • Central-difference formula (second order-accurate approximation): (df/dx)xi ≈[f(xi+ ∆x) -f(xi-∆x)] /(2∆x) +O(∆x 2) Second derivate (second order-accurate approximation) (d 2 f/dx 2)xi ≈[f(xi+ ∆x) - 2 f(xi) + f(xi-∆x)] /(∆x 2) +O(∆x 2)

Finite Difference analog to the partial derivates Partial derivatives of u at the (i, n)th node Forward Backward Central Forward

Finite Difference scheme Differential equations Estimating derivatives numerically Finite difference equations (algebraic equations)

Finite Differencing of Parabolic PDE’s Consider a simple example of a parabolic (or diffusion) partial differential equation with one spatial independent variable xЄ[x. A, x. B]: I. C. : u(x, 0)=uo(x) t>0 : B. C. 1: u(0, t)=u. A(t) B. C. 2: u(x. N, t)=u. B(t) with a (diffusion coefficient) constant.

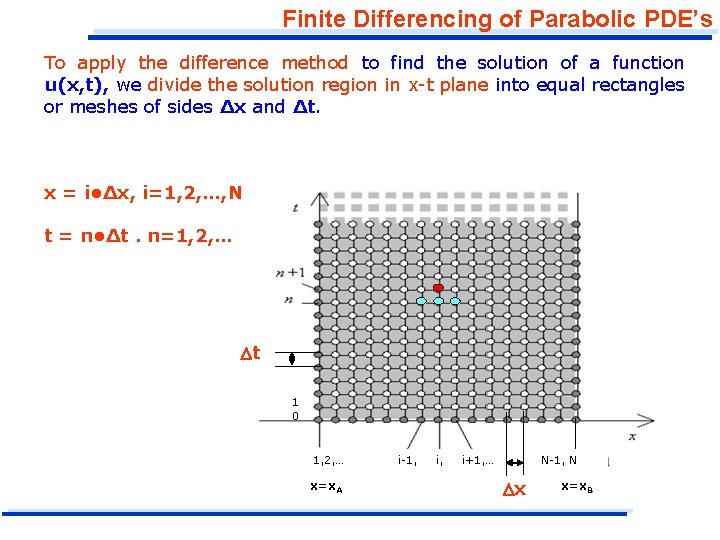
Finite Differencing of Parabolic PDE’s To apply the difference method to find the solution of a function u(x, t), we divide the solution region in x-t plane into equal rectangles or meshes of sides Δx and Δt. x = i • Δx, i=1, 2, …, N t = n • Δt. n=1, 2, … Dt 1 0 1, 2, … x=x. A i-1, i+1, … N-1, N Dx x=x. B

Finite Differencing of Parabolic PDE’s In the development of the analog finite difference equation we write All i and n Both sides must to be evaluated at the same conditions xi and tn. 1 0 1, 2, … x=x. A i-1, i, i+1, … N-1, N x=x. B Then we substitute the analog finite difference equation for each derivates.

Finite Difference analog to the partial derivates Partial derivatives of u at the (i, n)th node Forward Backward Central Forward

Finite Difference scheme Depending on analog finite difference equation used one can obtain different finite difference equations analogous to the: 1. Euler’s Method (explicit or forward) 2. Laasonen’s Method (implicit o backward) 3. Crank-Nicholson Method (implicit)

Finite Difference scheme Euler’s Method (explicit or forward) The forward or explicit difference equation is probably the most well known, although it is the least efficient of all the possible equations which can be used. We use the forward difference formula for the derivative with respective to t and central difference formula with respect to x.

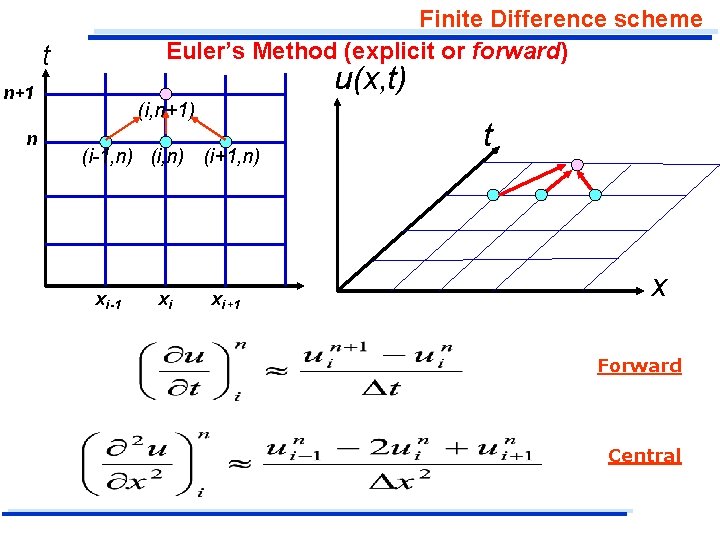
Finite Difference scheme Euler’s Method (explicit or forward) t u(x, t) n+1 n (i, n+1) (i-1, n) (i+1, n) xi-1 xi xi+1 t x Forward Central

Finite Difference scheme Euler’s Method (explicit or forward) t n+1 n Finite difference equation: (i, n+1) (i-1, n) (i+1, n) xi-1 xi xi+1 i=2…N-1 This equation contains only one unknown value, uin+1, and is written explicitly for this unknown. Therefore, this explicit formula can be used to compute u(xi, tn+1) explicitly in terms of u(xi, tn) for i=2. . N-1 (internal grid points). The computation of the values of the dependent variable is thus made one point at a time.

Finite Difference scheme Euler’s Method (explicit or forward) Finite difference equation: I. C. 1 0 1, 2, … i-1, i, i+1, … i=2…N-1 N-1, N The values of u along the first time row (n=0 or t=0) can be calculated in terms of the boundary and initial conditions, then the values of u along the second row (n=1 or t=Δt) are calculated in terms of the first time row, and so on:

Finite Difference scheme Euler’s Method (explicit or forward) The explicit formula is simple to implement, and especially easy to use for computing the value of u at each time level, but the its computation is slow. In general, a numerical solution must converge to the solution of the corresponding differential equation when the finite increments , x and t, are decreased in size. Analysis as shown that a very restrictive relationship between the size of Dx and that of Dt must be satisfied in order for the solution of forward equation to approach that of the differential equation. The restriction required that: One should use very small t and large x which results to a stable solution but with low accuracy (in order to minimize the truncation error in the x analogs (O ( x 2)), the size of x must be small).

Finite Difference scheme Euler’s Method (explicit or forward) The many transient problems which have boundary conditions independent of time approach a steady state condition. For these problems: xЄ[x. A, x. B]: I. C. : u(x, 0)=uo(x) t>0 : B. C. 1: u(0, t)=u. A B. C. 2: u(x. N, t)=u. B The time increment can be continuously increased and made quite large as the solution progresses towards steady state without causing significant truncation error in the time analog. However, for the forward difference equation, the size of t must remain on the order of ( x)2 for the solution to be stable. Thus, a very small value of t must be used for stability even when larger value could be used without causing truncation error. A finite difference equation which does not have this restriction is, therefore, a much better one to use as an analog to the differential equation

Finite Difference scheme Laasonen’s Method (implicit o backward) In searching for a new finite difference equation which does not have a restriction on the size of t for stability, we might write the finite differences analogs for the derivates at the new or unknown time which is indexed by n+1.

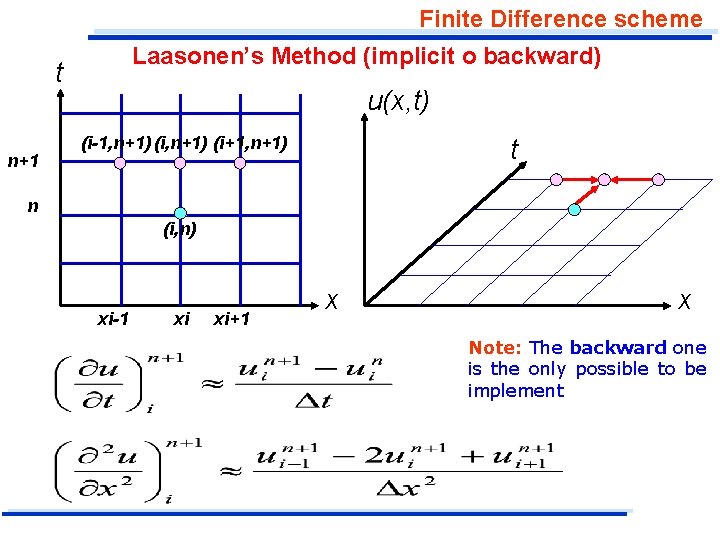
Finite Difference scheme Laasonen’s Method (implicit o backward) t n+1 u(x, t) (i-1, n+1) (i+1, n+1) t n (i, n) xi-1 xi xi+1 x x Note: The backward one is the only possible to be implement

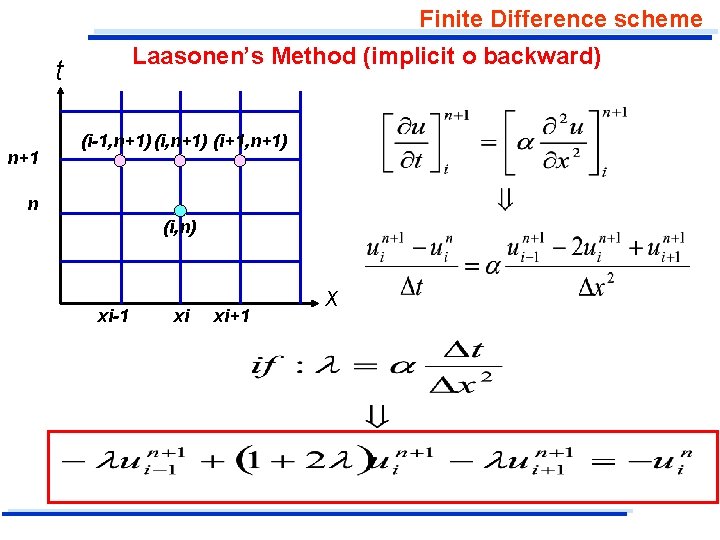
Finite Difference scheme Laasonen’s Method (implicit o backward) t n+1 (i-1, n+1) (i+1, n+1) n (i, n) xi-1 xi xi+1 x

Finite Difference scheme Laasonen’s Method (implicit o backward) (1) i=2…N-1 This equation is implicit; that is, it contains three values of the dependent values , u, at the unknown time level, n+1. For N-1 increments in x and the boundary conditions of equation: B. C. 1: u(0, t)=u. A; B. C. 2: u(x. N, t)=u. B there will be N-2 unknown values of u at each time level, and there are N-2 equations, one corresponding to each points. In summary: N-2 equations (1) for 2<=i<=N-1 B. C. 1 for i=1: u 1 n+1=u. A B. C. 2 for i=N: u. Nn+1=u. B

Finite Difference scheme Laasonen’s Method (implicit o backward) The resulting set of equation represents a linear system in which the coefficient matrix is tridiagonal. If N=7, for each time level, one should calculate uin+1 as: B. C 1: u 1 n+1=u. A B. C. 2: u 7 n+1=u. B The equation can thus be solved by the Thomas method to obtain N-2 values of uin+1. The same method can be used to obtain the values uin+2 from the now known values of uin+1

Finite Difference scheme Laasonen’s Method (implicit o backward) ØThere is no restriction on the size of t for stability of the backward difference equation. Ø The size of t can therefore be set, independently of the size of x, to minimize the truncation error of the Taylor series in time. ØAll the values of u at the first unknown time level (n=1) will be computed from the initial values (n=0). ØIn the solution of these equations on a digital computer, it is usual practice to keep the size of x constant throughout the calculation.

Finite Difference scheme Laasonen’s Method (implicit o backward) If the boundary conditions are of the form of equation: B. C. 1: u(0, t)=u. A; B. C. 2: u(x. N, t)=u. B so that the transient solution approaches a steady state condition, it is usual practice to increase the size of t as the solution progresses in order to obtain the solution in a minimum computing time. This is because as the steady-state conditions are approached, the difference in values of u from one time level to the next diminishes if a constant time increment is used. Similarly, as the steady-state conditions are approached, the size of second and the higher time derivates decrease; thus, the same truncation error will result from a larger t as the steady-state is approached.

Finite Difference scheme Laasonen’s Method (implicit o backward) üThe backward difference equation is an efficient one, and it is simple to use. üHowever, it is only first-order correct in time. first order-accurate second order-accurate approximation üIt is desirable to find a second-order correct analog to this derivates

Finite Difference scheme Crank-Nicholson Method (implicit) In the Crank-Nicholson equation all the finite difference are written about the point (xi, tn+1/2) (point designated by a cross) which is halfway between the known and the unknown time levels. Values of the dependent variable, u, are computed only at the points designated by circles. t (i-1, n+1) (i+1, n+1) n+1 + n+1/2 n (i-1, n) (i, n) xi-1 xi (i+1, n) xi+1 x

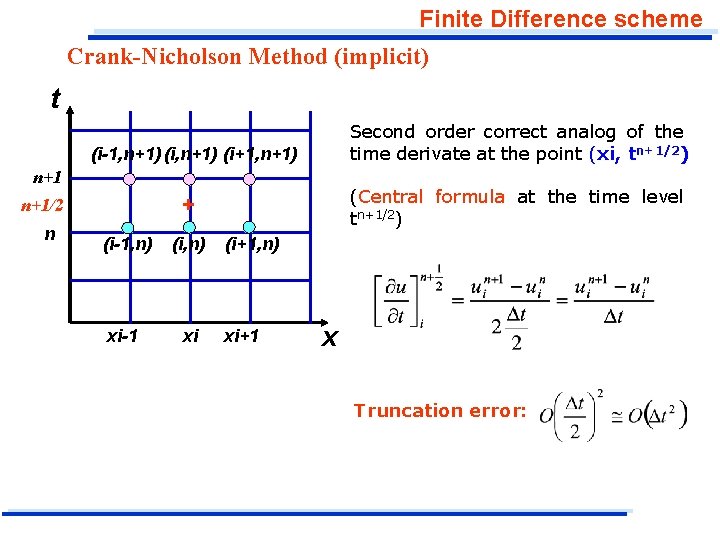
Finite Difference scheme Crank-Nicholson Method (implicit) t Second order correct analog of the time derivate at the point (xi, tn+1/2) (i-1, n+1) (i+1, n+1) n+1 n (Central formula at the time level tn+1/2) + n+1/2 (i-1, n) (i, n) xi-1 xi (i+1, n) xi+1 x Truncation error:

Finite Difference scheme t Crank-Nicholson Method (implicit) (i-1, n+1) (i+1, n+1) The second order space derivate at the point (xi, tn+1/2) n+1 + n+1/2 n (i-1, n) (i, n) xi-1 xi (i+1, n) xi+1 The second order space derivate at the point (xi, tn+1/2) is approximated by the arithmetic average of the central difference formulas at the point (xi, tn) and (xi, tn+1) x

Finite Difference scheme Crank-Nicholson Method (implicit) Crank-Nicholson finite difference equation which is second-order correct in both x and t:

Finite Difference scheme Crank-Nicholson Method (implicit) This equation is implicit as it contains the same three unknown values of u that are found in the backward difference equation. Similarly, this equation and its two boundary conditions can be solved by the Thomas method. t u(x, t) (i-1, n+1) (i+1, n+1) t n+1 + n+1/2 n (i-1, n) xi-1 (i, n) xi (i+1, n) xi+1 x x

Finite Difference scheme Crank-Nicholson Method (implicit) ØThe Crank-Nicholson Method requires more computations per time step than the backward difference method to evaluate the right side of the equation (this side contains values of u at three length positions at the known time level instead of the one value found in the backward difference equation. ØHowever, a larger time increment can be used for the Crank-Nicholson equation , since its time derivate analog is second order correct, fewer time steps are thus necessary to computes values of the dependent variable for a given elapsed time. ØThus the Crank-Nicholson equation is more efficient than the backward difference method and is the preferred method for obtaining numerical solutions to parabolic differential equations.

Finite Difference scheme Crank-Nicholson Method (implicit) The Crank-Nicholson equation, like the backward difference equation, is stable for all ratios of x to t.

Finite Difference scheme Crank-Nicholson Method (implicit) In matrix form the system of equations becomes Vector of unknown values Vector of known values

Finite Difference scheme Crank-Nicholson Method (implicit) The resulting set of equation represents a linear system in which the coefficient matrix is tridiagonal. If N=7, for each time level, one should calculate uin+1 as: B. C 1: u 1 n+1=u. A B. C. 2: u 7 n+1=u. B The equation can thus be solved by the Thomas method to obtain N-2 values of uin+1. The same method can be used to obtain the values uin+2 from the now known values of uin+1

Numerical methods to solve parabolic PDEs: Boundary conditions

Boundary conditions 2° order PDE 2 independent variables Linear with constant coefficients is a diffusion coefficient I. C. : t = 0 u(x, 0) = u 0(x) The boundary conditions for partial differential equations of second order must to be two and they can arise as expressions containing the values of the unknown function u and / or its first derivatives ∂u/∂x

Boundary conditions Dirichlet condition The condition of the Dirichlet is the simplest case of boundary conditions. In general, it provides the boundary conditions for the possible dependence on the time variable through the function C (t) and F (t) (which can also be constant) B. C. 1: x=0 -> u(t, x=0)=C(t) all t (simple case) B. C. 2: x=L -> u(t, x=L)=F(t) all t (simple case) We write the finite difference equation at the internal nodes of the domain including the nodes adjacent to the boundary (i=2…N-1). Then in this equations we replace the value of the function on the boundary value (known) imposed by the condition.

Boundary conditions Dirichlet condition Example: I. C. : t = 0 u(x, 0) = u 0(x) B. C. 1: x=0 -> u(t, x=0)=C(t) all t (simple case) B. C. 2: x=L -> u(t, x=L)=F(t) all t (simple case) where C(t) and F(t) can be also constant

Boundary conditions Dirichlet condition Example: Laasonen’s Method (implicit o backward) (1) i=2…N-1 B. C 1: x=0: u 1 n+1=u. A(t) B. C. 2: x=L: u. Nn+1=u. B(t) N°eq=(N-2) (1) + 2 BC = N 1 x=0 2 N-1 N x=L

Boundary conditions Neumann condition The case of the Neumann condition differs from the previous by the fact that the unknown function is also unknown on the boundary, on which, however, the derivative is known. Therefore, for the same discrete grid, you must obtain one equation more (for each Neumann condition) than in the Dirichlet case.

Boundary conditions Neumann condition Example: I. C. : t = 0 u(x, 0) = u 0(x) B. C. 1: x=0 -> u(t, x=0)=C(t) all t (simple case) B. C. 2: x=L -> u(t, x=L) ->(∂u/∂x)=q all t (simple case) where q is known The finite-difference equation must be write, as in the previous case, for all internal nodes (i=2. . N-1), and the boundary condition will provide an additional equation for the unknown value of the function on the boundary

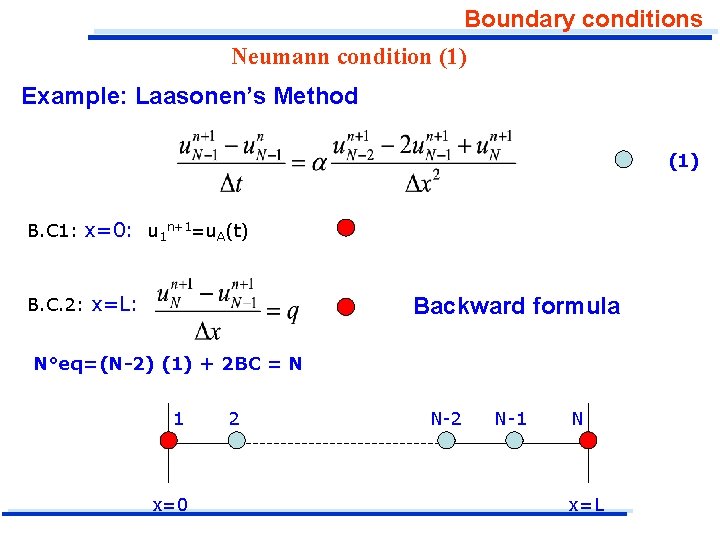
Boundary conditions Neumann condition (1) Example: Laasonen’s Method (1) B. C 1: x=0: u 1 n+1=u. A(t) B. C. 2: x=L: Backward formula N°eq=(N-2) (1) + 2 BC = N 1 x=0 2 N-1 N x=L

Boundary conditions Neumann condition Backward formula B. C. 2: x=L: Note: The expression used for the first derivative, being "backward" and not central, is only accurate to first order. To improve this aspect, it is useful to write a formula that is central to the position of the edge (i=N), which is when we know the value of the first derivative. This node can be obtained by considering an outside "fictitious node".

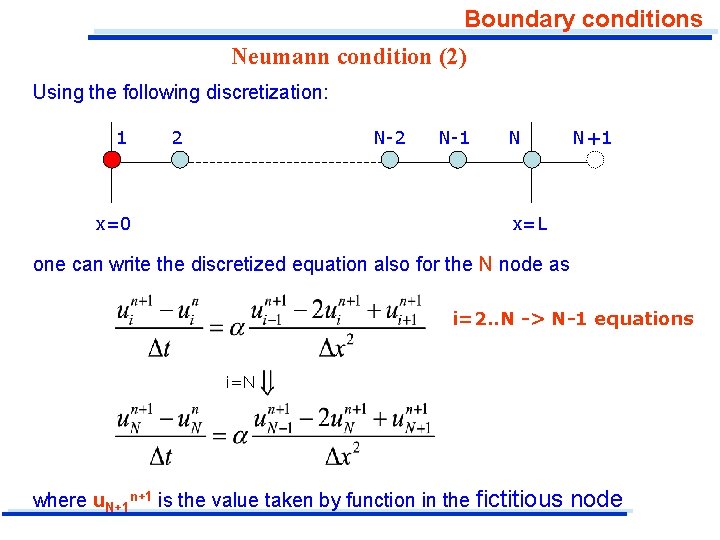
Boundary conditions Neumann condition (2) Using the following discretization: 1 2 N-2 x=0 N-1 N N+1 x=L one can write the discretized equation also for the N node as i=2. . N -> N-1 equations i=N where u. N+1 n+1 is the value taken by function in the fictitious node

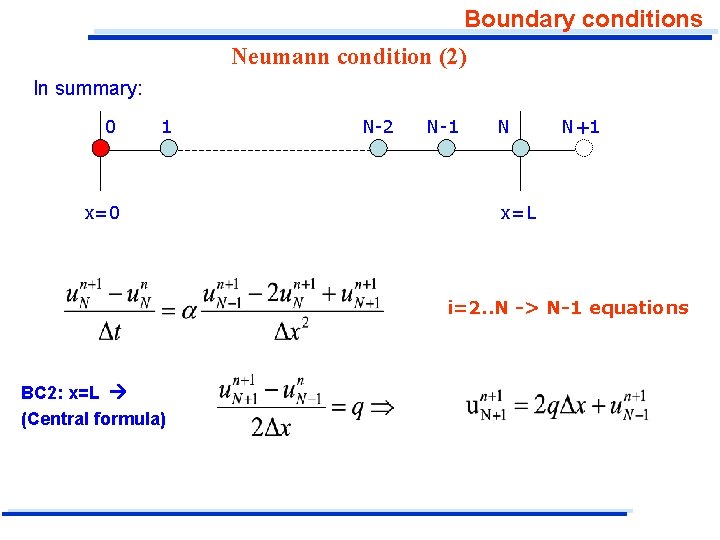
Boundary conditions Neumann condition (2) In summary: 0 1 x=0 N-2 N-1 N N+1 x=L i=2. . N -> N-1 equations BC 2: x=L (Central formula)

Boundary conditions Neumann condition Dx In summary: 0 x=0 1 N-2 N-1 Dx N N+1 x=L Again we have N equations in N unknowns, and thus all of the formulas employed for the derivatives of space are the second order. It should also be noted that the formula used for the first derivative is formally second order accurate, but for a double-interval (2 x).

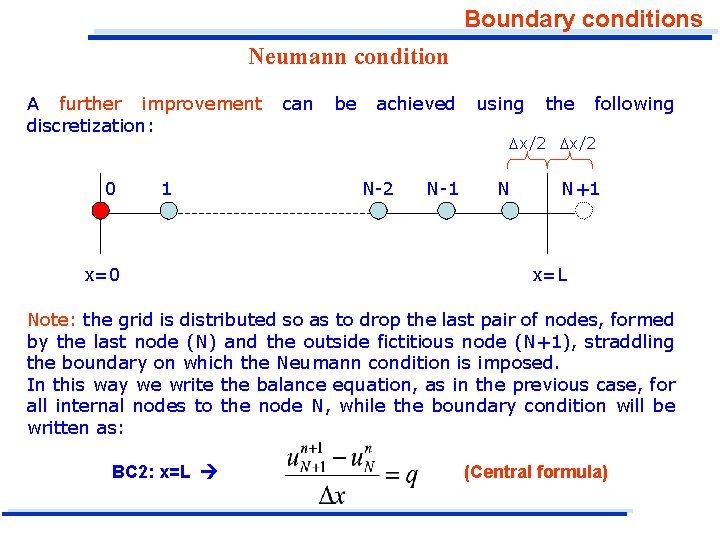
Boundary conditions Neumann condition A further improvement discretization: 0 1 x=0 can be achieved using the following x/2 N-2 N-1 N N+1 x=L Note: the grid is distributed so as to drop the last pair of nodes, formed by the last node (N) and the outside fictitious node (N+1), straddling the boundary on which the Neumann condition is imposed. In this way we write the balance equation, as in the previous case, for all internal nodes to the node N, while the boundary condition will be written as: BC 2: x=L (Central formula)

Boundary conditions Neumann condition (3) In summary: 0 x=0 x/2 1 N-2 N-1 N N+1 x=L i=2. . N -> N-1 equations BC 2: x=L Central and therefore accurate to second order, and for a range of x. The latter method is thus preferable to others when the Neumann condition is "pure“, that is, not involving the boundary value of the function.

Boundary conditions Third type” or “mixed condition The flow is not assigned as a value (q), but is determined by an exchange coefficient multiplied by a driving force which is a function of the unknown value taken by the function on the edge, thus giving rise to a boundary condition known as “third type” or “mixed“. Example It will be more natural adopt the second method, which involves both the fictitious node and the node at the edge.

Convergence and stability of FDM for 2° order linear parabolic Equations Definition of convergence U(x, t) is the exact solution of partial differential problem in IR 't. u is the exact solution of finite difference equations used to approximate the differential problem. Intuitively, it is expected to be a "good" method when: u->U when x, t ->0 More precisely, one can say for example that, if uin is the value of u calculated at the point (xi, tn) of the integration domain, and if then the finite difference method is said to be convergent. If U is the vector generated by evaluating U(xi, tn), then U-u is said to be the discretization error, and is the direct consequence of the truncation error in finite difference formulas.

Convergence and stability of FDM for 2° order linear parabolic Equations Definition of numerical stability u is the exact solution of finite difference equations used to approximate the differential problem ũ is the numerical solution of the same problem As a result of rounding errors (roundoff) introduced by the machine is always: u≠ũ A method is said to be stable if (ũ –u) does not diverges as the number of discretization nodes increases. ØEuler’s method is stable when: (Stability Parameter) ØBoth Laasonen’s Method and Crank-Nicholson equations, are stable for all ratios of x to t. (Stability Parameter)

Convergence and stability of FDM for 2° order linear parabolic Equations Definition of consistency A finite difference scheme is called consistent if, making the limit for finite increments of the independent variables that tend to zero, it returns the differential expression that you want to approximate. Note: all the three schemes examined in this course are consistent. Of course, what matters is the construction of methods which can prove the convergence, since at the end the only solution is becoming available is the numerical one which, hopefully, is close to the exact one. Convergence Lax’s theorem A finite difference method for a second order linear PDE schemes that use consistent scheme, and that is numerically stable, is convergent.

Parabolic PDE’s Parabolic (or diffusion) PDE with one spatial independent variable: general form t Є [0, +∞] x Є [x. A, x. B] I. C. : u(t=0, x)=u*(x) all x B. C. 1: u(t, x=x. A)=u. A(t) all t (simple case) B. C. 2: u(t, x=x. B)=u. B(t) all t (simple case) Analytical solution: u=u(t, x) where u is a continuous function of t and x

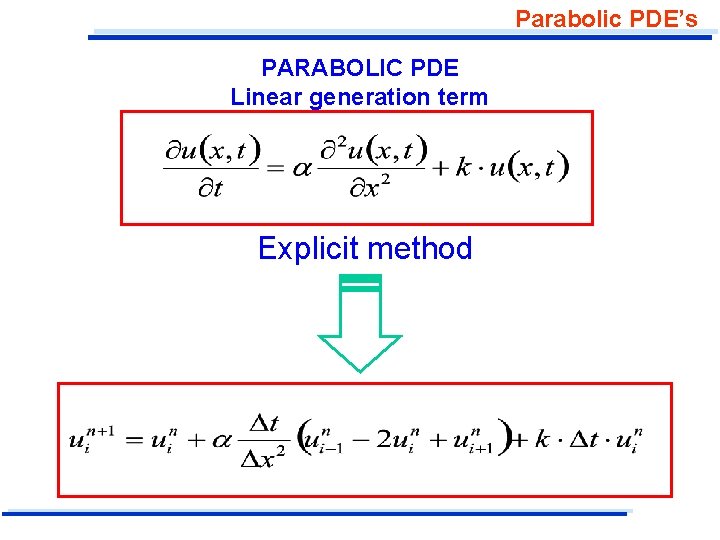
Parabolic PDE’s PARABOLIC PDE Linear generation term Explicit method