Electric Potential III Fields Potential Conductors Potential and

Electric Potential (III) - Fields - Potential - Conductors

Potential and Continuous Charge Distributions We can use two completely different methods: 1. 2. Or, Find from Gauss’s Law, then…

Ex 1: Given V=3 x 2+12 x-1, find where E=0.

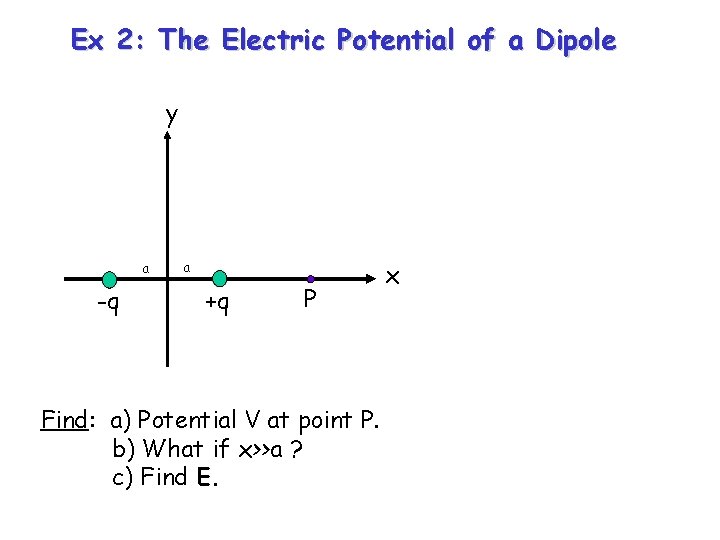
Ex 2: The Electric Potential of a Dipole y a -q a +q P Find: a) Potential V at point P. b) What if x>>a ? c) Find E. x

Solution

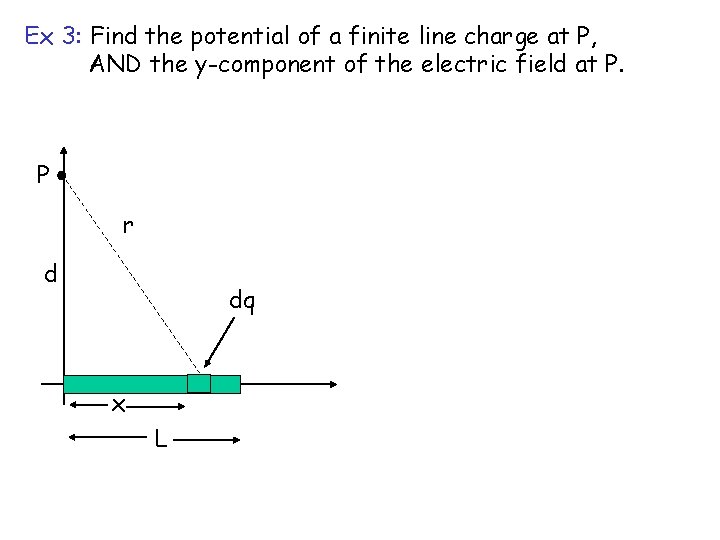
Ex 3: Find the potential of a finite line charge at P, AND the y-component of the electric field at P. P r d dq x L

Solution

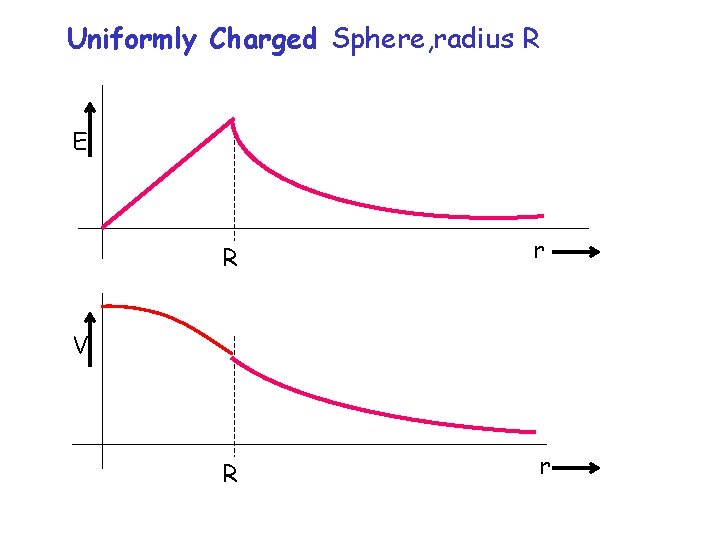
Ex 3: Find the potential of a uniformly charged sphere of radius R, inside and out. R

Uniformly Charged Sphere, radius R E R r V

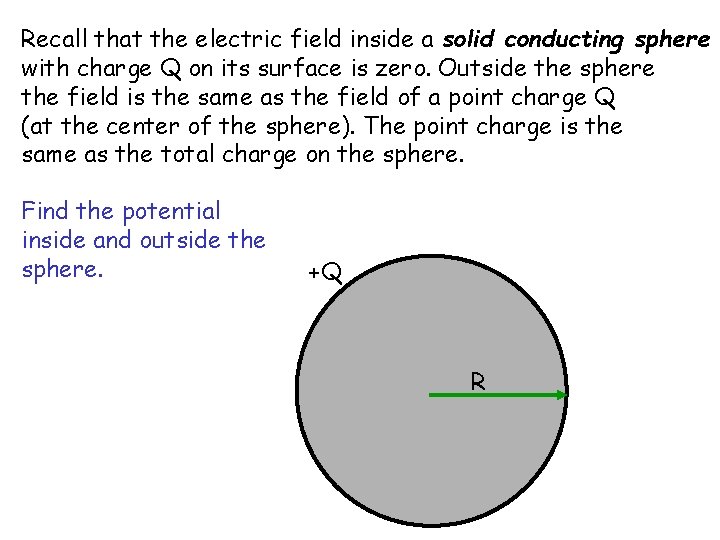
Recall that the electric field inside a solid conducting sphere with charge Q on its surface is zero. Outside the sphere the field is the same as the field of a point charge Q (at the center of the sphere). The point charge is the same as the total charge on the sphere. Find the potential inside and outside the sphere. +Q R

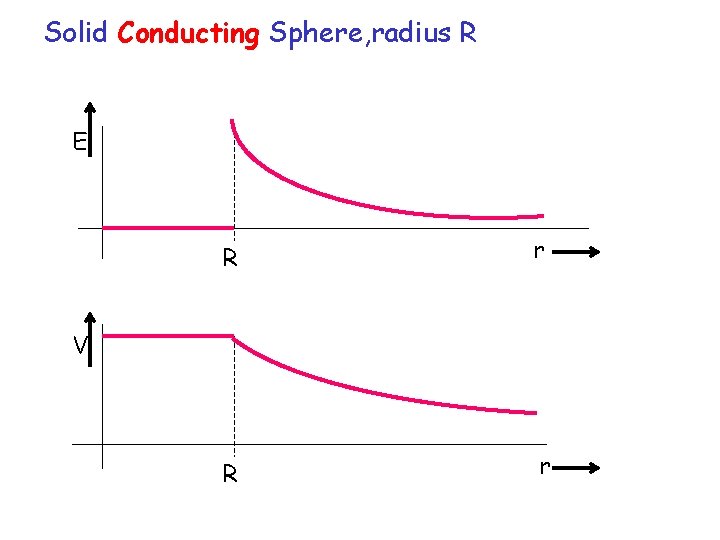
Solution -Inside (r<R), E=0, integral of zero = constant, so V=const -Outside (r>R), E is that of a point charge, integral gives V=k. Q/r

Solid Conducting Sphere, radius R E R r V

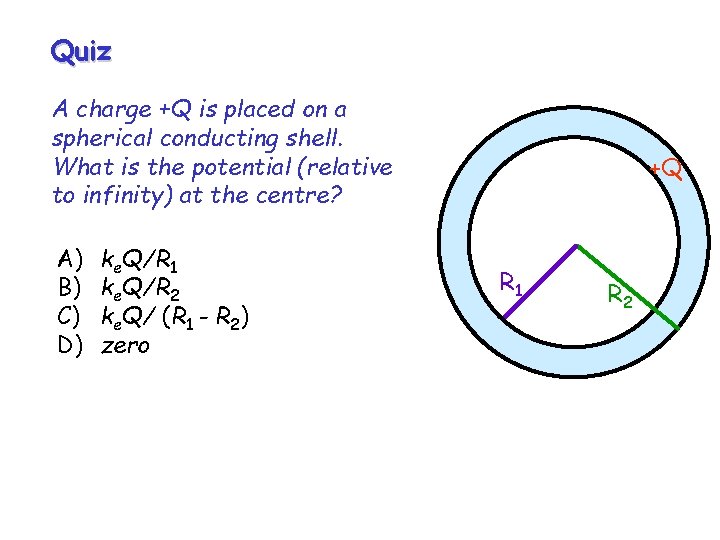
Quiz A charge +Q is placed on a spherical conducting shell. What is the potential (relative to infinity) at the centre? A) B) C) D) ke. Q/R 1 ke. Q/R 2 ke. Q/ (R 1 - R 2) zero +Q R 1 R 2

Calculating V from Sources: i) Point source: (note: V 0 as r ) or ii) Several point sources: (Scalar) iii) Continuous distribution: OR … I. Find from Gauss’s Law (if possible) II. Integrate, (a “line integral”)