Static Electricity Electric Forces Electric Fields Electric Potential

Static Electricity, Electric Forces, Electric Fields, Electric Potential Energy, Electric Potential, Capacitors

Electric Charges • • Electrons have a negative charge Protons have a positive charge Charge is measured in “coulombs” “q” or “Q” in an equation is used for charge • 1 electron has 1. 6 x 10 -19 C of charge

Static Electricity • Static Electricity is the study of “charges at rest”. • Fundamental Rule of Charge – Opposite charges attract, – Like charges repel • 3 methods of charging : friction, conduction, & induction • Conductors allow electrons to move freely, Insulators do not!

Methods of Charging • Charging by friction scrapes electrons off one object and places them on the other (the two objects will have equal and opposite charges) • Charging by induction requires no contact. A charged object is brought near a neutral object and the charges in the neutral object become polarized (opposites attract and likes repel) so that neutral object behaves as if it is charged (but really it still has same # of + & - charges, so still neutral) • Charging by conduction requires contact. A charged object comes in contact with a neutral object and charges are transferred between objects until they both have equal charge (charge equilibrium)

Electrostatic Forces (F) (measured in Newtons) Given 2 charges of magnitude q 1 & q 2 separated by a distance d, the magnitude of the force that each of the charges exerts on the other is calculated by the relationship given by Coulomb’s Law. The direction of the force is determined by the fundamental law of charges (i. e. attraction or repulsion). The forces must be equal and opposite … Newton’s 3 rd Law! q 1 F F + F Coulomb’s Law: q 2 - d + + q 1 q 2 F k = 9 x 109 N*m 2/C 2 This is known as “Coulomb’s constant”

Electric Fields (E) measured in Newtons per Coulomb • Electric fields are the “energy field” that surrounds any charged particle” • Any other charge in this field will experience a force. • Electric fields are vectors (mag. & dir. ) • The direction of an Electric field is defined by the direction of the force on a “+” test charge placed in that field, thus Electric fields are always in a direction that is away from “+” and toward “-”. • Electric Field strength is measured in units of N/C (newtons per coulomb)

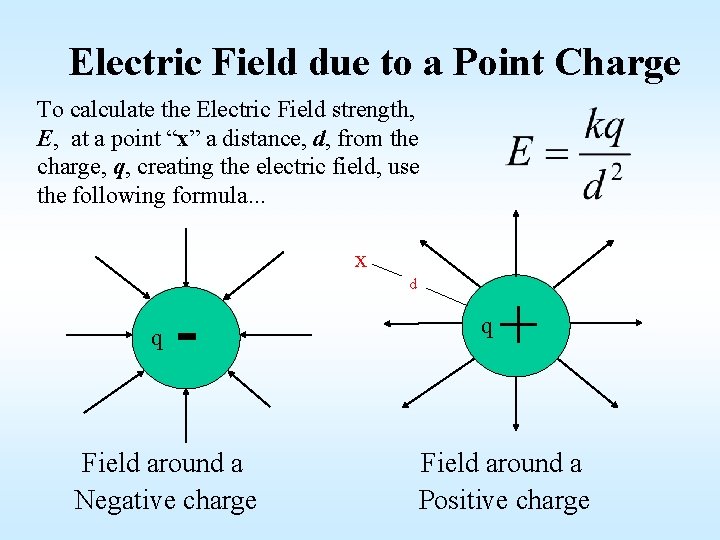
Electric Field due to a Point Charge To calculate the Electric Field strength, E, at a point “x” a distance, d, from the charge, q, creating the electric field, use the following formula. . . x q - Field around a Negative charge d q + Field around a Positive charge

Force on a charge due to an Electric Field If a charge, q, is placed at point “x” in the field where the Electric Field strength is E, it will experience a force F. F E + q d Q +

Electric Potential Energy (Uelec) measured in Joules When two charges are placed near each other, they have the potential to start moving under the influence of the force between them. If they have the “potential” to have “kinetic energy” then according to the Law of Conservation of Energy, they must have Potential Energy when they are in that arrangement. To calculate the potential energy of this arrangement of charges… q 1 + d q 2 - Remember: energy of any kind is always a scalar quantity…magnitude only!

Electric Potential (V) measured in Volts • Electric Potential (V) is defined as the Electric Potential Energy (Uelec) per unit of charge (q) at a given point in an Electric Field. • Electric Potential (V) is a scalar quantity, so…magnitude only but may be positive or negative based on the sign of the charge creating the field. • 1 volt = 1 joule per coulomb (1 V=1 J/C) To calculate the electric potential at a point in space due to a single point charge, use… …where Q is the charge creating the field and q is any charge that might be at the point in space of interest.

Equipotential Lines • Equipotential lines are “lines of equal energy” • All points on each line have the same electric potential (V) • Equipotential lines are usually parallel to the surface of the charge • They do not depend on the sign of the charge For a point charge, they are concentric circles. q Equipotential lines, each line has a different potential (V)

Uniform Electric Fields +Q + -Q E - + - + - d V 1 V 2 ΔV = V 1 -V 2 Uniform Electric fields exist when there are equal and oppositely charged plates separated by a distance, d. Each charged plate has a different value of electric potential (V 1 and V 2), often determined by connecting the plates to the terminals of a battery. The individual values of electric potential (V) are not important but the potential difference between the plates (ΔV) is very important. The electric fields created by each charged plate combine such that total electric field that has a constant value (E) at all regions between them. The relationship between the potential difference, V, electric field, E, and distance, d is… Note: This formula is ONLY valid for uniform fields!

Work done moving a charge through an Electric Field (W) - measured in Joules V 2 q V 1 + - + + + V 1 V 2 - If a charge is moving through an electric field, it experiences a force in the direction of the field that pushes it across equipotential lines. The charge moves through a distance, d, between its starting and final points and has a different potential (V) at the beginning and end, thus ΔV. Since there is a force moving an object through a distance, work is done on the charge. The following relationships apply.

Capacitors • A device used to store charge (energy) • Made of 2 conductors separated by an insulator • Each conductor carries an equal but opposite charge, q • Releases all charge (stored energy) in one big burst…think camera flash!

Capacitance (C) measured in farads • Capacitance is the quantity that describes the ability of a capacitor to store energy in the form of electric charge. • Or…The capacitance is the capacity of the capacitor • Capacitance depends on the amount of charge stored on each plate and the potential difference between the plates. • It is measured in units of Farads (F), named for Michael Faraday (a famous Physicist). To calculate the capacitance, C, simply find the ratio of the charge stored on a single plate, Q, and the potential difference between the plates, ΔV. Note: 1 Farad = 1 Coulomb / Volt Also, a Farad is a very large unit so usually use μF (10 -6), n. F (10 -9), or p. F (10 -12).

An example of a simple capacitor: (parallel-plate capacitor) 2 oppositely charged plates + E - To get more stored charge: + - • increase the size of the plates + - • decrease the plate separation + - • increase the voltage of the battery + - Insulator such as air, paper, plastic, or mylar