Electric Potential Electric Potential Energy Electric Potential Energy

Electric Potential & Electric Potential Energy

Electric Potential Energy n The electrostatic force is a conservative (=“path independent”) force n It is possible to define an electrical potential energy function with this force n Work done by a conservative force is equal to the negative of the change in potential energy

Work and Potential Energy There is a uniform field between the two plates n As the positive charge moves from A to B, work is done n n WAB=F d =q E d n ΔPE =-W AB=-q E d n only for a uniform field

Potential Difference (=“Voltage Drop”) n The potential difference between points A and B is defined as the change in the potential energy (final value minus initial value) of a charge q moved from A to B divided by the size of the charge n ΔV = VB – VA = ΔPE /q n Potential difference is not the same as potential energy

Potential Difference, cont. Another way to relate the energy and the potential difference: ΔPE = q ΔV n Both electric potential energy and potential difference are scalar quantities n Units of potential difference n n. V n = J/C A special case occurs when there is a uniform electric field n VB – VA= -Ed n Gives more information about units: N/C = V/m

Energy and Charge Movements A positive charge gains electrical potential energy when it is moved in a direction opposite the electric field n If a charge is released in the electric field, it experiences a force and accelerates, gaining kinetic energy n n n As it gains kinetic energy, it loses an equal amount of electrical potential energy A negative charge loses electrical potential energy when it moves in the direction opposite the electric field

Energy and Charge Movements, cont When the electric field is directed downward, point B is at a lower potential than point A n A positive test charge that moves from A to B loses electric potential energy n It will gain the same amount of kinetic energy as it loses potential energy n

Summary of Positive Charge Movements and Energy n When a positive charge is placed in an electric field It moves in the direction of the field n It moves from a point of higher potential to a point of lower potential n Its electrical potential energy decreases n Its kinetic energy increases n

Summary of Negative Charge Movements and Energy n When a negative charge is placed in an electric field It moves opposite to the direction of the field n It moves from a point of lower potential to a point of higher potential n Its electrical potential energy decreases n Its kinetic energy increases n

Example: A proton moves from rest in an electric field of 8. 0 104 V/m along the +x axis for 50 cm. Find a) the change in in the electric potential, b) the change in the electrical potential energy, and c) the speed after it has moved 50 cm. a) V=-Ed=-(8. 0 104 V/m)(0. 50 m)=-4. 0 104 V b) PE=q V=(1. 6 10 -19 C)(-4. 0 104 V)=-6. 4 10 -15 J KEi+PEi=KEf+PEf, KEi=0 KEf=PEi-PEf=- PE, mpv 2/2=6. 4 10 -15 J mp=1. 67 10 -15 kg

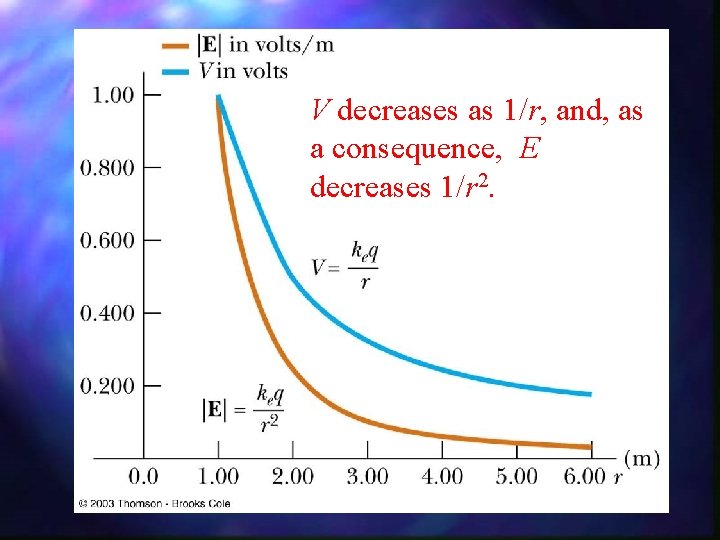
16. 2 Electric Potential of a Point Charge n The point of zero electric potential is taken to be at an infinite distance from the charge n The potential created by a point charge q at any distance r from the charge is if r , V=0 and if r=0, V

V decreases as 1/r, and, as a consequence, E decreases 1/r 2.

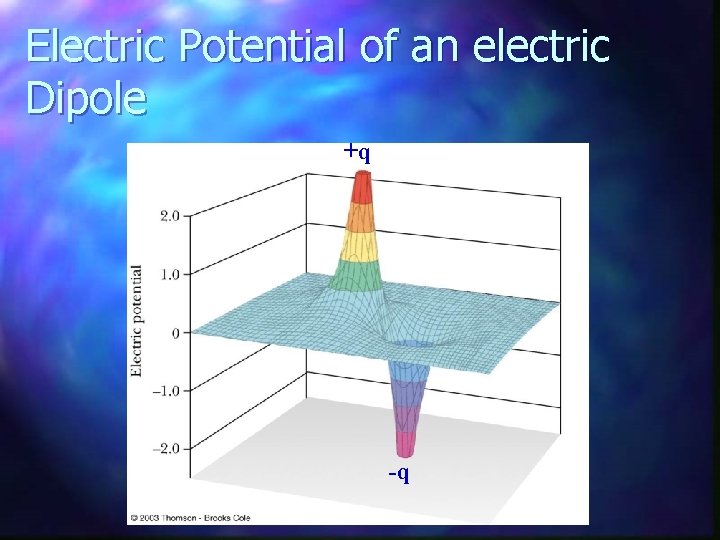
Electric Potential of an electric Dipole +q -q

Electric Potential of Multiple Point Charges n Superposition principle applies n The total electric potential at some point P due to several point charges is the algebraic sum of the electric potentials due to the individual charges n The algebraic sum is used because potentials are scalar quantities

Electrical Potential Energy of Two Charges n V 1 is the electric potential due to q 1 at some point P 1 The work required to bring q 2 from infinity to P 1 without acceleration is q 2 E 1 d = q 2 V 1 n This work is equal to the potential energy of the two particle system n

Notes About Electric Potential Energy of Two Charges n If the charges have the same sign, PE is positive n n n Positive work must be done to force the two charges near one another The like charges would repel If the charges have opposite signs, PE is negative n n The force would be attractive Work must be done to hold back the unlike charges from accelerating as they are brought close together

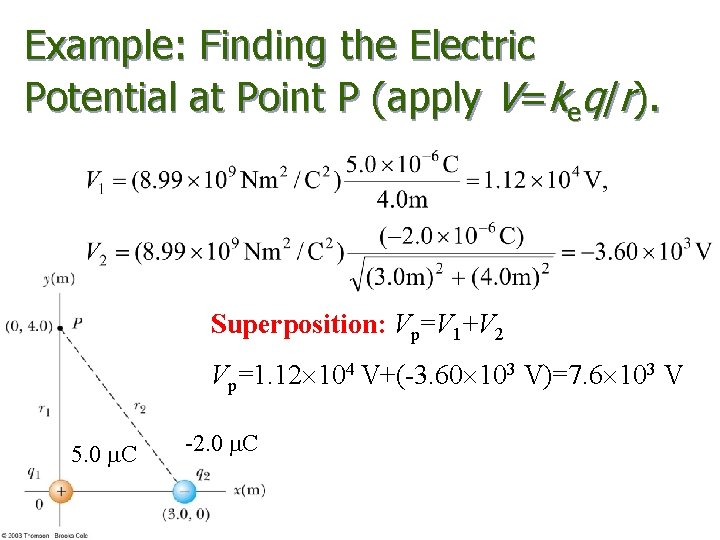
Example: Finding the Electric Potential at Point P (apply V=keq/r). Superposition: Vp=V 1+V 2 Vp=1. 12 104 V+(-3. 60 103 V)=7. 6 103 V 5. 0 m. C -2. 0 m. C

Problem Solving with Electric Potential (Point Charges) n Remember that potential is a scalar quantity n n Use the superposition principle when you have multiple charges n n Take the algebraic sum Keep track of sign n n So no components to worry about The potential is positive if the charge is positive and negative if the charge is negative Use the basic equation V = keq/r

Potentials and Charged Conductors n. W =- PE= -q(VB – VA) , no work is required to move a charge between two points that are at the same electric potential W=0 when VA=VB n All points on the surface of a charged conductor in electrostatic equilibrium are at the same potential n Therefore, the electric potential is a constant everywhere on the surface of a charged conductor in equilibrium

Overview: Conductors in Equilibrium n n n The conductor has an excess of positive charge All of the charge resides at the surface E = 0 inside the conductor The electric field just outside the conductor is perpendicular to the surface The potential is a constant everywhere on the surface of the conductor The potential everywhere inside the conductor is constant and equal to its value at the surface

The Electron Volt n The electron volt (e. V) is defined as the energy that an electron (or proton) gains when accelerated through a potential difference of 1 V n n Electrons in normal atoms have energies of 10’s of e. V Excited electrons have energies of 1000’s of e. V High energy gamma rays have energies of millions of e. V 1 V=1 J/C 1 e. V = 1. 6 x 10 -19 J

Equipotential Surfaces n An equipotential surface is a surface on which all points are at the same potential No work is required to move a charge at a constant speed on an equipotential surface n The electric field at every point on an equipotential surface is perpendicular to the surface n

Equipotentials and Electric Fields Lines (Positive Charge): The equipotentials for a point charge are a family of spheres centered on the point charge n The field lines are perpendicular to the electric potential at all points n

Equipotentials and Electric Fields Lines (Dipole): n Equipotential lines are shown in blue n Electric field lines are shown in orange n The field lines are perpendicular to the equipotential lines at all points