Fungsi Persamaan Fungsi Linear dan Fungsi Kuadrat RELASI

Fungsi, Persamaan Fungsi Linear dan Fungsi Kuadrat

RELASI DAN FUNGSI Kompetensi Dasar : Mendeskripsikan perbedaan konsep relasi dan fungsi Indikator : 1. Konsep relasi dan fungsi dibedakan dengan jelas 2. Jenis-jenis fungsi diuraikan ditunjukkan contohnya Adaptif

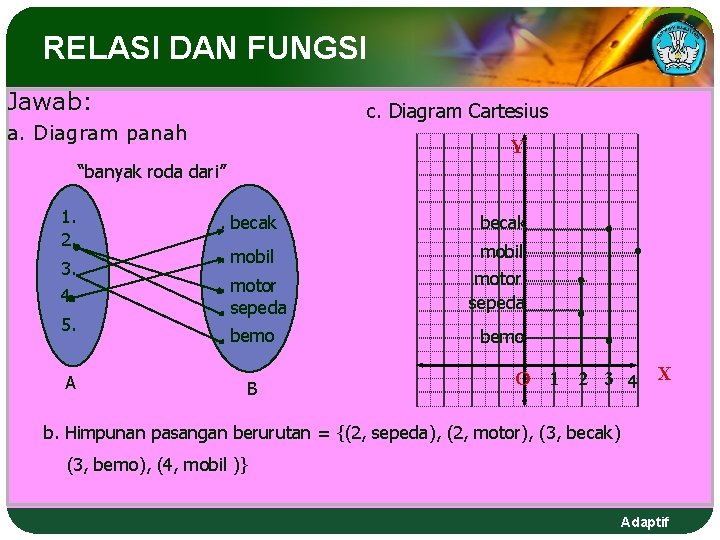
RELASI DAN FUNGSI Ada 3 cara dalam menyatakan suatu relasi : 1. Diagram panah 2. Himpunan pasangan berurutan 3. Diagram Cartesius Contoh: Diketahui himpunan A = {1, 2, 3, 4, 5} dan himpunan B = {becak, mobil, sepeda, motor, bemo}. Relasi yang menghubungkan himpunan A ke himpunan B adalah “banyak roda dari”. Tunjukkan relasi tersebut dengan: a. Diagram panah b. Himpunan pasangan berurutan c. Diagram Cartesius Adaptif

RELASI DAN FUNGSI Jawab: c. Diagram Cartesius a. Diagram panah Y “banyak roda dari” 1. 2. 3. 4. 5. A . becak . mobil . motor. sepeda. bemo B motor sepeda bemo • • • O 1 2 3 4 X b. Himpunan pasangan berurutan = {(2, sepeda), (2, motor), (3, becak) (3, bemo), (4, mobil )} Adaptif

RELASI DAN FUNGSI Pengertian Fungsi : Suatu fungsi f dari himpunan A ke himpunan B adalah suatu relasi yang memasangkan setiap elemen dari A secara tunggal , dengan elemen pada B . . . A f B Adaptif

RELASI DAN FUNGSI Beberapa cara penyajian fungsi : v Dengan diagram panah v f : D K. Lambang fungsi tidak harus f. Misalnya, un = n 2 + 2 n atau u(n) = n 2 + 2 n v Dengan diagram Kartesius v Himpunan pasangan berurutan v Dalam bentuk tabel Adaptif

RELASI DAN FUNGSI Contoh : grafik fungsi Gambarlah grafik sebuah fungsi : f: x f(x) = x 2 dengan Df = {– 2, – 1, 0, 1, 2}, Rf = {0, 1, 4}. Y (– 2, 4) (– 1, 1) (1, 1) O (0, 0) v 4 disebut bayangan (peta) dari 2 dan juga dari – 2. v – 2 dan 2 disebut prapeta dari 4, dan dilambangkan f– 1(4) = 2 atau – 2. v Grafik Kartesius merupakan grafik fungsi y=f(x) hanya apabila setiap garis sejajar sumbu- Y yang memotong grafik hanya memotong di tepat satu titik saja. X Adaptif

RELASI DAN FUNGSI Beberapa Fungsi Khusus v v v v 1). Fungsi Konstan 2). Fungsi Identitas 3). Fungsi Modulus 4). Fungsi Genap dan Fungsi Ganjil Fungsi genap jika f( x) = f(x), dan Fungsi ganjil jika f( x) = f(x) 5). Fungsi Tangga dan Fungsi Nilai Bulat Terbesar [[ x ] = {b | b x < b + 1, b bilangan bulat, x R} Misal, jika 2 x < 1 maka [[x] = 2 6). Fungsi Linear 7). Fungsi Kuadrat 8). Fungsi Turunan Adaptif

RELASI DAN FUNGSI Jenis Fungsi 1. Injektif ( Satu-satu) Fungsi f: A B adalah fungsi injektif apabila setiap dua elemen yang berlainan di A akan dipetakan pada dua elemen yang berbeda di B. Misalnya Fungsi f(x) = 2 x adalah fungsi satu-satu dan f(x) = x 2 bukan suatu fungsi satu-satu sebab f(-2) = f(2). 2. Surjektif (Onto) Fungsi f: A B maka apabila f(A) B dikenal fungsi into. Jika f(A) = B maka f adalah suatu fungsi surjektif. Fungsi f(x) = x 2 bukan fungsi yang onto 3. Bijektif (Korespondensi Satu-satu) Apabila f: A B merupakan fungsi injektif dan surjektif maka “f adalah fungsi yang bijektif” Adaptif

FUNGSI LINEAR 1. Bentuk Umum Fungsi Linear Fungsi ini memetakan setiap x a ≠ 0, a dan b konstanta. R kesuatu bentuk ax + b dengan Grafiknya berbentuk garis lurus yang disebut grafik fungsi linear dengan Persamaan y = mx + c, m disebut gradien dan c konstanta 2. Grafik Fungsi Linear Cara menggambar grafik fungsi linear ada 2 : 1. Dengan tabel 2. Dengan menentukan titik- titik potong dengan sumbu x dan sumbu y Adaptif

FUNGSI LINEAR Contoh : Suatu fungsi linear ditentukan oleh y = 4 x – 2 dengan daerah asal {x -1 x 2, x R}. a. Buat tabel titik-titik yangmemenuhi persamaan diatas. b. Gambarlah titik-titik tersebut dalam diagram Cartesius. c. Tentukan titik potong grafik dengan sumbu X dan sumbu Y. Jawab a. Ambil sembarang titik pada domain X -1 0 1 2 Y = 4 x-2 -6 -2 2 6 Jadi, grafik fungsi melalui titik-titik (-1, -6), (0, -2), (1, 2), (2, 6) Adaptif

FUNGSI LINEAR Y b. c. Titik potong dengan sumbu x ( y= 0 ) y = 4 x – 2 6 0 = 4 x - 2 • 2 = 4 x x= 2 • -2 -1 O 1 2 • -2 Jadi titik potong dengan sumbu X adalah ( ½, 0) X Titik potong dengan sumbu Y ( x = 0 ) y = 4 x – 2 y = 4(0) – 2 y = -2 Jadi titik potong dengan sumbu Y adalah (0, -2) • -6 Adaptif

FUNGSI LINEAR 3. Gradien Persamaan Garis Lurus Cara menentukan gradien : (i). Persamaan bentuk y = mx+c, gradiennya adalah m. (ii). Persamaan bentuk ax+by+c=0 atau ax+by=-c adalah m= (iii). Persamaan garis lurus melalui dua titik (x 1, y 1) dan (x 2, y 2), gradiennya adalah m = Contoh : 1. Tentukan gradien persamaan garis berikut 2. a. y = 3 x – 4 3. b. 2 x – 5 y = 7 4. 2. Tentukan gradien garis yang melalui pasangan titik (-2, 3) dan (1, 6) Adaptif

FUNGSI LINEAR Jawab : 1 a. Y = 3 x – 4 gradien = m = 3 b. 2 x - 5 y = 7, a = 2 dan b = - 5 m = = - 2. m = = 1 Adaptif

FUNGSI LINEAR 4. Menentukan Persamaan Garis Lurus v Persamaan garis melalui sebuah titik (x 1, y 1) dan gradien m adalah y – y 1 = m ( x – x 1 ) v Persamaan garis melalui dua titik (x 1, y 1) dan (x 2, y 2) adalah = Contoh 1 : Tentukan persamaan garis yang melalui titik ( -2, 1 ) dan gradien -2 Jawab : y – y 1 = m ( x – x 1 ) y – 1 = -2 ( x – (-2)) y - 1 = -2 x – 4 y = -2 x - 3 Adaptif

FUNGSI LINEAR Contoh 2 : Tentukan persamaan garis yang melalui titik P(-2, 3) dan Q(1, 4) Jawab : = = = 3(y – 3) = 1(x + 2) 3 y – 9 = x + 2 3 y - x – 11 = 0 Adaptif

FUNGSI LINEAR 5. Kedudukan dua garis lurus v Dua garis saling berpotongan jika m 1 ≠ m 2 v Dua garis saling sejajar jika m 1 = m 2 v Dua garis saling tegak lurus jika m 1. m 2 = -1 atau m 1 = Contoh : 1. Tentukan persamaan garis lurus yang melalui titik (2, -3) dan sejajar dengan garis x – 2 y + 3 = 0 2. Tentukan persamaan garis lurus yang melalui titik (-3, 5) dan tegak lurus pada 6 x – 3 y – 10 = 0 Adaptif

FUNGSI LINEAR Jawab : 1. Diketahui persamaan garis x – 2 y + 3 = 0 maka Persamaan garis melalui titik (2, -3) dan gradien y – y 1 = m ( x – x 1) y+3 =½(x– 2) y+3 =½x– 1 2 y + 6 = x – 2 y – 8 = 0 adalah Jadi persamaan garis lurus yang sejajar dengan garis x – 2 y + 3 = 0 dan melalui titik (2, -3) adalah x – 2 y – 8 = 0 Adaptif

FUNGSI LINEAR 2. Diketahui persamaan garis 6 x – 3 y – 10 = 0. Persamaan garis lurus yang dicari melalui titik (-3, 5) dan bergradien -½, maka persamaannya adalah y – y 1 = m(x – x 1) y – 5 = -½ (x + 3) y – 5 = -½x 2 y – 10 = -x – 3 x + 2 y – 10 + 3 = 0 x + 2 y – 7 = 0 Jadi, persamaan garis lurus yang melalui titik (-3, 5) dan tegak lurus garis 6 x – 3 y – 10 = 0 adalah x + 2 y – 7 = 0. Adaptif

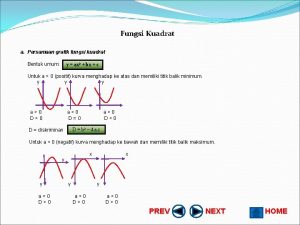
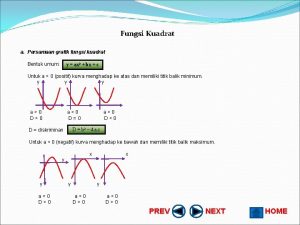
FUNGSI KUADRAT 1. Bentuk umum fungsi kuadrat y = f(x) ax 2+bx+c dengan a, b, c R dan a 0 Grafik fungsi kuadrat berbentuk parabola simetris 2. Sifat-sifat Grafik Fungsi Kuadrat Berdasarkan nilai a (i) Jika a > 0 (positif), maka grafik terbuka ke atas. Fungsi kuadrat memiliki nilai ekstrim minimum, dinotasikan ymin atau titik balik minimum. (ii) Jika a < 0 (negatif), maka grafik terbuka ke bawah. Fungsi kuadrat memiliki nilai ekstrim maksimum, dinotasikan ymaks atau titik balik maksimum. Adaptif

FUNGSI KUADRAT Berdasarkan Nilai Diskriminan (D) Nilai diskriminan suatu persamaan kuadrat adalah D = b 2 – 4 ac Hubungan antara D dengan titik potong grafik dengan sumbu X (i) Jika D > 0 maka grafik memotong sumbu X di dua titik yang berbeda. (ii) Jika D = 0 maka grafik menyinggung sumbu X di sebuah titik. (iii) Jika D < 0 maka grafik tidak memotong dan tidak menyinggung sumbu X. Adaptif

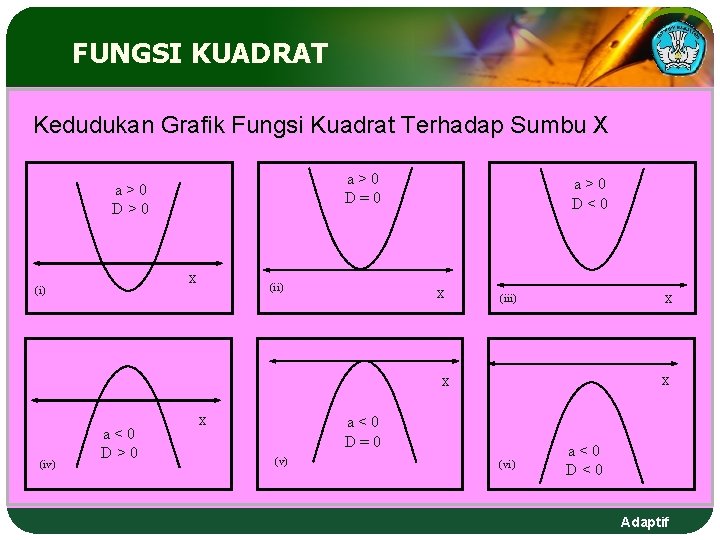
FUNGSI KUADRAT Kedudukan Grafik Fungsi Kuadrat Terhadap Sumbu X a>0 D=0 a>0 D>0 X (i) (ii) a>0 D<0 X (iii) X X X (iv) a<0 D>0 a<0 D=0 X (v) (vi) a<0 D<0 Adaptif

FUNGSI KUADRAT 3. Menggambar Grafik Fungsi Kuadrat Langkah-langkah menggambar grafik fungsi kuadrat : (i) Menentukan titik potong dengan sumbu X (y = 0) (ii) Menentukan titik potong dengan sumbu Y (x = 0) (iii) Menentukan sumbu simentri dan koordinat titik balik • Persamaan sumbu simetri adalah x = • Koordinat titik puncak / titik balik adalah (iv) Menentukan beberapa titik bantu lainnya (jika di perlukan) Adaptif

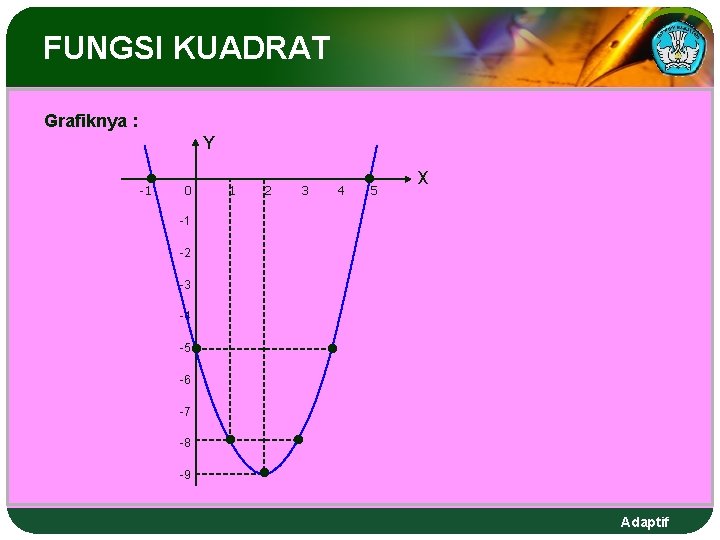
FUNGSI KUADRAT Contoh : Gambarlah grafik fungsi kuadrat y = x 2 – 4 x – 5. Jawab : (i) Titik potong dengan sumbu X (y = 0) x 2 – 4 x – 5 = 0 (x + 1)(x – 5) = 0 x = -1 atau x = 5 Jadi, titik potong grafik dengan sumbu X adalah titik (-1, 0) dan (5, 0). (ii) (iv) Titik potong dengan sumbu Y (x = 0) y = 02 – 4(0) – 5 y = -5 (v) Jadi titik potong dengan sumbu Y adalah titik ( 0, -5 ) (vi) Adaptif

FUNGSI KUADRAT (iii) Sumbu simetri dan koordinat titik balik Jadi, sumbu simetrinya x = 2 dan koordinat titik baliknya (2, -9). (iv) Menentukan beberapa titik bantu. Misal untuk x = 1, maka y = -8. Jadi, titik bantunya (1, -8). Adaptif

FUNGSI KUADRAT Grafiknya : Y • -1 0 1 2 3 4 • 5 X -1 -2 -3 -4 -5 • • -6 -7 -8 -9 • • • Adaptif

FUNGSI KUADRAT Persamaan fungsi kuadrat f(x) =ax 2 + bx + c apabila diketahui grafik fungsi melalui tiga titik Contoh: Tentukan fungsi kuadrat yang melalui titik (1, -4), (0, -3) dan (4, 5) Jawab: f(x) = ax 2 + bx + c f(1) = a(1)2 + b(1) + c = -4 a + b + c = -4. . . 1) f(0) = a(0)2 + b(0) + c = -3 0 + c = -3. . . 2) f(4) = a(4)2 + b(4) + c = 5 16 a + 4 b + c = =5. . . 3) Adaptif

FUNGSI KUADRAT Substitusi 2) ke 1) a + b – 3 = -4 a + b = -1. . . 4) Substitusi 2) ke 3) 16 a + 4 b – 3 = 5 16 a + 4 b = 8. . . 5) Dari 4) dan 5) diperoleh : a + b = -1 x 4 4 a + 4 b = -4 16 a + 4 b = 8 x 1 16 a + 4 b = 8 _ -12 a = -12 a = 1 Substitusi a = 1 ke 4) 1 + b = -1 b = -2 Jadi, fungsi kuadratnya adalah f(x) = x 2 -2 x -3 Adaptif

FUNGSI KUADRAT Persamaan fungsi kuadrat f(x) = ax 2 + bx + c apabila diketahui dua titik potong terhadap sumbu X dan satu titik lainnya dapat ditentukan dengan rumus berikut. Contoh : Tentukan persamaan fungsi kuadrat yang memotong sumbu X di titik A (1, 0), B(-3, 0), dan memotong sumbu Y di titik (0, 3) Adaptif

FUNGSI KUADRAT Jawab : Titik (1, 0) dan (-3, 0) disubstitusikan ke f(x) menjadi : f(x) = a(x – 1)(x + 3). . . 1) Kemudian subsitusikan (0, 3) ke persamaan 1) menjadi : 3 = a(0 - 1)(x + 3) 3 = -3 a a = -1 Persamaan fungsi kuadratnya menjadi : Jadi fungsi kuadratnya adalah Adaptif

FUNGSI KUADRAT Persamaan fungsi kuadrat f(x) = ax 2 + bx + c apabila diketahui titik puncak grafik (xp’ yp) dan satu titik lainnya dapat ditentukan dengan rumus berikut. Adaptif

FUNGSI KUADRAT Contoh : Tentukan persamaan fungsi kuadrat yang titik puncaknya (-1, 9) dan melalui (3, -7) Jawab : f(x) = a(x – xp)2 + yp f(x) = a(x + 1 )2 + 9 (xp , yp) = (-1, 9) . . . 1) Subsitusikan titik (3, -7) ke persamaan -7 = a(3 + 1)2 + 9 -16 = 16 a a= 1 1) menjadi : Adaptif

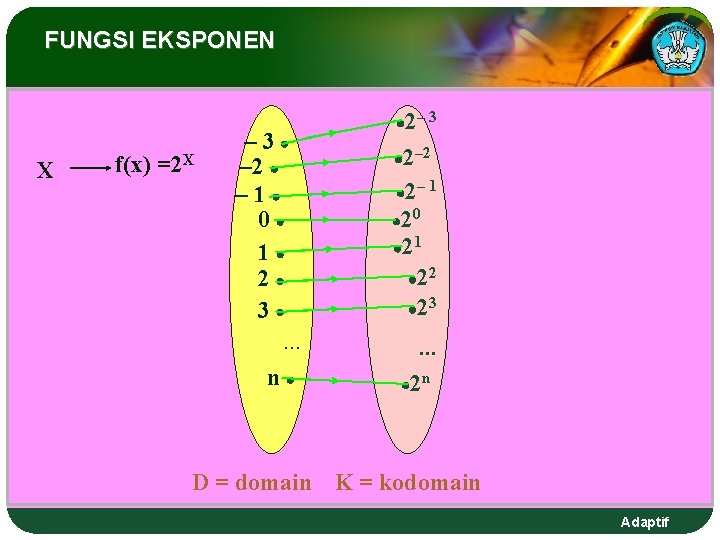
FUNGSI EKSPONEN X f(x) =2 X – 3 – 2 – 1 0 1 2 3 . . . n 2– 3 2– 2 2– 1 20 21 22 23 . . . 2 n D = domain K = kodomain Adaptif

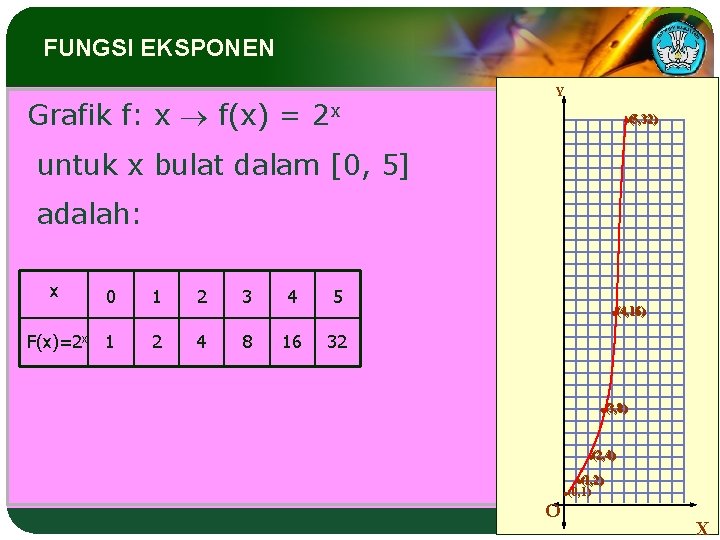
FUNGSI EKSPONEN Grafik f: x f(x) = 2 x Y (5, 32) untuk x bulat dalam [0, 5] adalah: x 0 1 2 3 4 5 F(x)=2 x 1 2 4 8 16 32 (4, 16) (3, 8) (2, 4) (1, 2) (0, 1) O Adaptif X

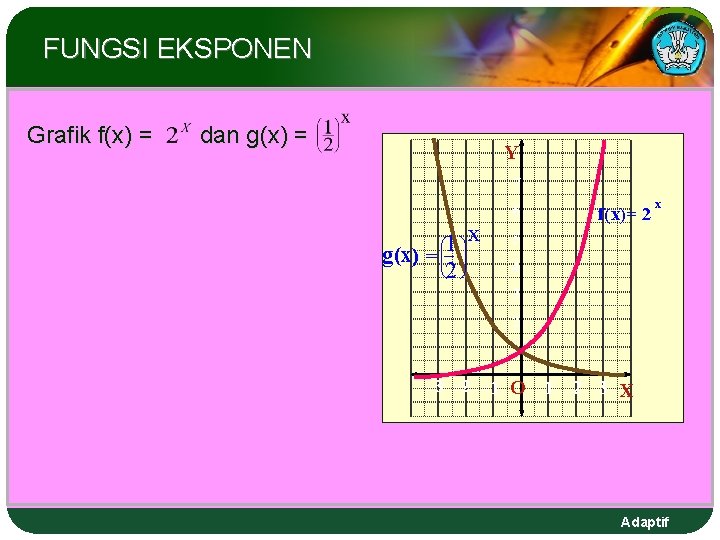
FUNGSI EKSPONEN Grafik f(x) = dan g(x) = Y 7 6 g(x) æ = çç è 1 ö÷x 2 ÷ø f(x)= 2 x 5 4 3 2 1 – 3 – 2 – 1 O 1 2 3 X Adaptif

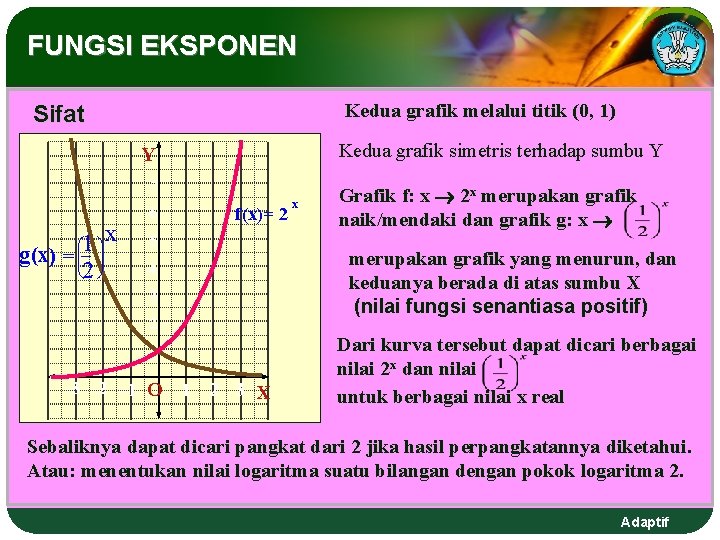
FUNGSI EKSPONEN Kedua grafik melalui titik (0, 1) Sifat Kedua grafik simetris terhadap sumbu Y Y 7 g(x) æ = çç è 1 ö÷x 2 ÷ø 6 f(x)= 2 5 Grafik f: x 2 x merupakan grafik naik/mendaki dan grafik g: x merupakan grafik yang menurun, dan keduanya berada di atas sumbu X (nilai fungsi senantiasa positif) 4 3 2 1 – 3 – 2 – 1 O x 1 2 3 X Dari kurva tersebut dapat dicari berbagai nilai 2 x dan nilai untuk berbagai nilai x real Sebaliknya dapat dicari pangkat dari 2 jika hasil perpangkatannya diketahui. Atau: menentukan nilai logaritma suatu bilangan dengan pokok logaritma 2. Adaptif

FUNGSI LOGARITMA v Logaritma merupakan kebalikan dari eksponen. Fungsi logaritma juga merupakan kebalikan dari fungsi eksponen. Secara umum fungsi logaritma didefinisikan sebagai berikut : Untuk a > 1, a R Adaptif

FUNGSI LOGARITMA Secara visual grafik fungsi eksponen dan fungsi logaritma adalah sebagai berikut : Y o X Adaptif

FUNGSI LOGARITMA Contoh 1 : Nyatakan persamaan berikut ke dalam bentuk logaritma yang ekivalen a. 8 = 23 b. ¼ = 2 -2 Jawab : a. 8 = 23 b. ¼ = 2 -2 log 8 = 3 2 log ¼ = -2 2 Contoh 2 : Nyatakan persamaan berikut ke dalam bentuk perpangkatan yang ekuivalen a. 4 = 2 log 16 b. -6 = 2 log Jawab : a. 4 = 2 log 16 24 = 16 b. -6 = 2 log 2 -6 = Adaptif

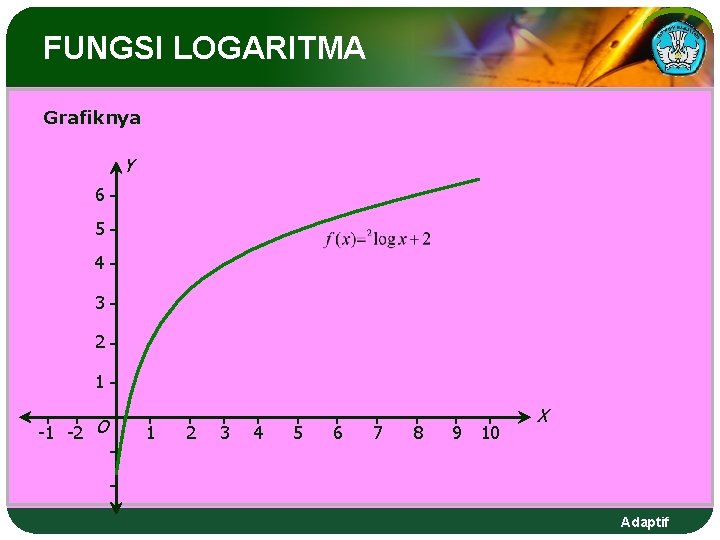
FUNGSI LOGARITMA Contoh 3 : Gambarkan grafik fungsi f(x) = 2 log x+2 Jawab : Sebelum menggambar grafik kita dapat menggunakan bantuan tabel berikut. x f(x) = 2 log x+2 ¼ 0 ½ 1 1 2 2 3 4 4 8 5 Adaptif

FUNGSI LOGARITMA Grafiknya Y 6 5 4 3 2 1 -1 -2 O 1 2 3 4 5 6 7 8 9 10 X Adaptif

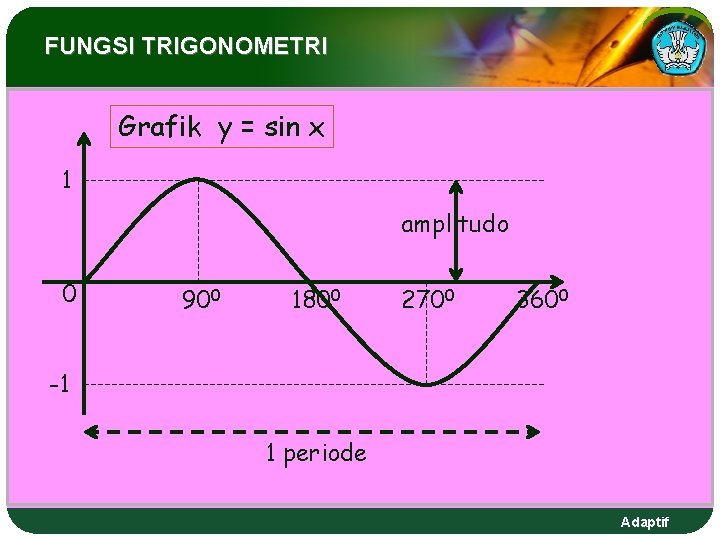
FUNGSI TRIGONOMETRI Grafik y = sin x 1 amplitudo 0 900 1800 2700 3600 -1 1 periode Adaptif

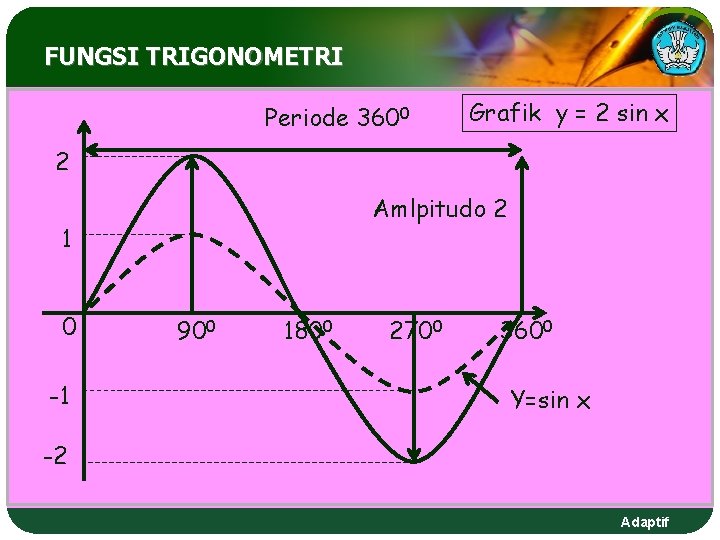
FUNGSI TRIGONOMETRI Periode 3600 Grafik y = 2 sin x 2 Amlpitudo 2 1 0 -1 900 1800 2700 3600 Y=sin x -2 Adaptif

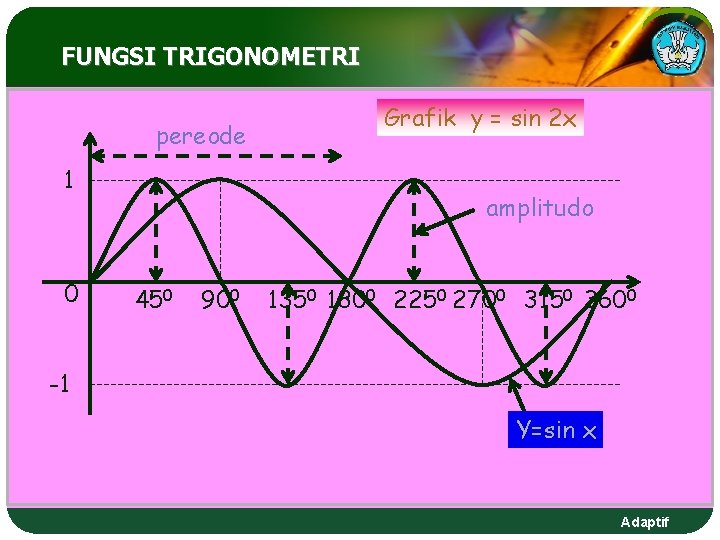
FUNGSI TRIGONOMETRI pereode 1 0 Grafik y = sin 2 x amplitudo 450 900 1350 1800 2250 2700 3150 3600 -1 Y=sin x Adaptif

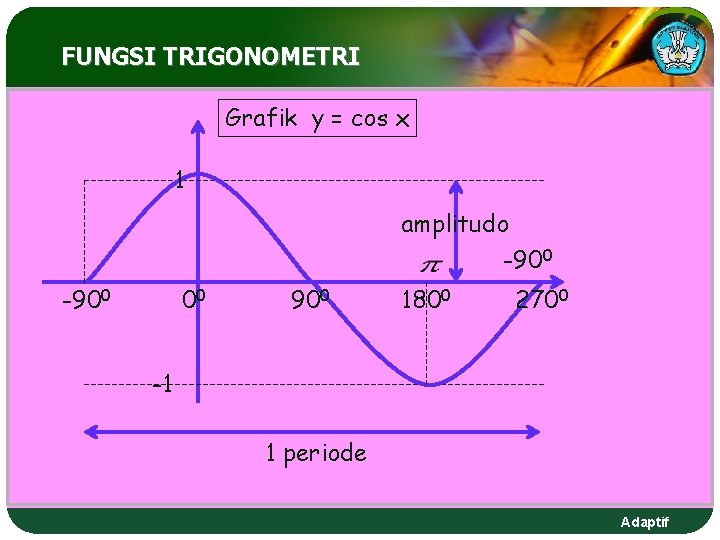
FUNGSI TRIGONOMETRI Grafik y = cos x 1 amplitudo -900 00 900 1800 2700 -1 1 periode Adaptif

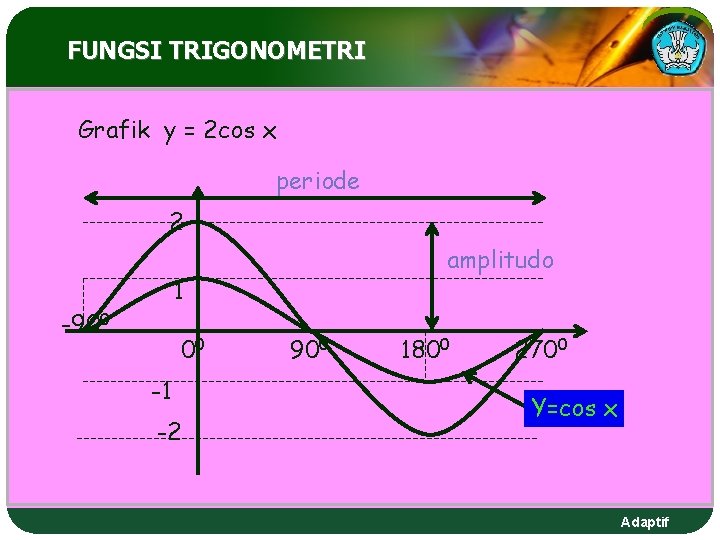
FUNGSI TRIGONOMETRI Grafik y = 2 cos x periode 2 amplitudo 1 -900 00 -1 -2 900 1800 2700 Y=cos x Adaptif