SOLUSI PERSAMAAN NON LINEAR METODE BISEKSI BAGI DUA

SOLUSI PERSAMAAN NON LINEAR METODE BISEKSI (BAGI DUA)

Metode Biseksi n n Ide awal metode ini adalah metode table, dimana area dibagi menjadi N bagian. Hanya saja metode biseksi ini membagi range menjadi 2 bagian, dari dua bagian ini dipilih bagian mana yang mengandung dan bagian yang tidak mengandung akar dibuang. Hal ini dilakukan berulang-ulang hingga diperoleh akar persamaan.

Metode Biseksi

Metode Biseksi n n Untuk menggunakan metode biseksi, terlebih dahulu ditentukan batas bawah (a) dan batas (b). Kemudian dihitung nilai tengah : x= Dari nilai x ini perlu dilakukan pengecekan keberadaan akar. Secara matematik, suatu range terdapat akar persamaan bila f(a) dan f(b) berlawanan tanda atau dituliskan : f(a). f(b) < 0

Metode Biseksi * Dari nilai X yang di dapat perlu dilakukan pengecekkan akar, keberadaan akar yakni : Jika f(x). f(a) < 0, maka b = x, f(b) = f(x), a = tetap atau f(x). f(b) < 0, maka a = x, f(a) = f(x), b = tetap n Setelah diketahui dibagian mana terdapat akar, maka batas bawah dan batas di perbaharui sesuai dengan range dari bagian yang mempunyai akar.

Akar persamaan biasanya di tentukan berdasarkan iterasi maksimum yang diberikan, tetapi yang paling banyak digunakan yakni dengan menentukaan toleransi error (e) yang di tetapkan.

Algoritma Biseksi

Contoh Soal n Tentukanlah satu akar dari persamaan pangkat tiga berikut ini ; f(x) = X 3 + X 2 – 3 x - 3 = 0

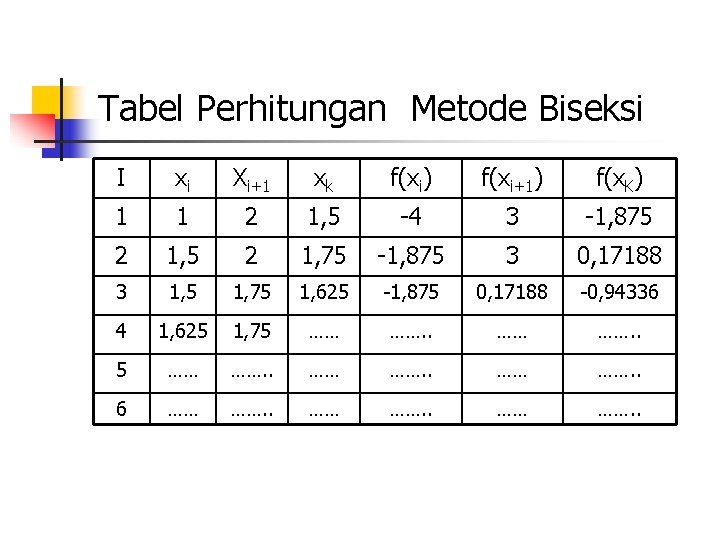
Tabel Perhitungan Metode Biseksi I xi Xi+1 xk f(xi) f(xi+1) f(x. K) 1 1 2 1, 5 -4 3 -1, 875 2 1, 75 -1, 875 3 0, 17188 3 1, 5 1, 75 1, 625 -1, 875 0, 17188 -0, 94336 4 1, 625 1, 75 …… ……. . 6 …… ……. .

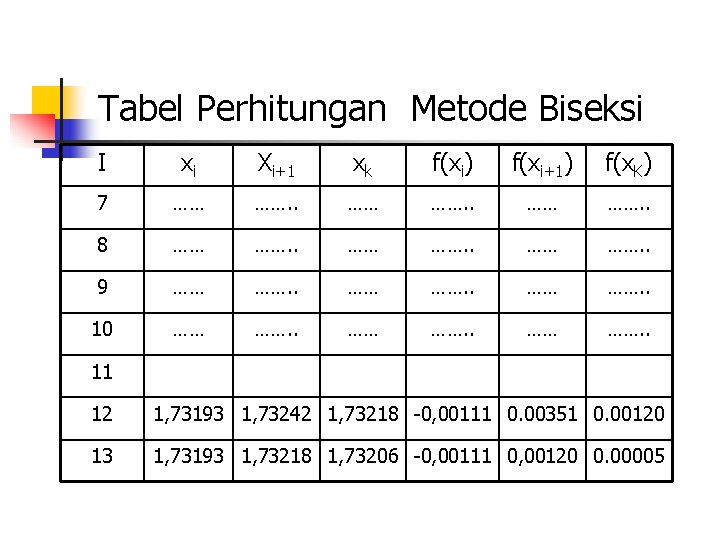
Tabel Perhitungan Metode Biseksi I xi Xi+1 xk f(xi) f(xi+1) f(x. K) 7 …… ……. . 8 …… ……. . 9 …… ……. . 10 …… ……. . 11 12 1, 73193 1, 73242 1, 73218 -0, 00111 0. 00351 0. 00120 13 1, 73193 1, 73218 1, 73206 -0, 00111 0, 00120 0. 00005

Keuntungan BISEKSI n Selalu berhasil menemukan akar (solusi) yang dicari, atau dengan kata lain selalu konvergen

Kelemahan Biseksi n Bekerja sangat lambat. Tidak memandang bahwa sebenarnya akar atau solusi yang dicari telah berada dekat sekali dengan X 0 ataupun X 1

Contoh Soal n n n Dimana x = Pada iterasi ke 13 diperoleh x = 1, 73206 dan f(x) = 0. 00005 Untuk menghentikan iterasi, dapat dilakukan dengan menggunakan toleransi error atau iterasi maksimum. Catatan : Dengan menggunakan metode biseksi dengan tolerasi error 0. 0001 dibutuhkan 13 iterasi, semakin teliti (kecil toleransi errorny) maka semakin besar jumlah iterasi yang dibutuhkan.

Contoh Soal n n Selesaikan persamaan xe-x+1 = 0, dengan menggunakan range x=[-1, 0], Dengan toleransi error 0, 001 atau iterasi maksimum yang di tentukan adalah 10 iterasi

Contoh Soal Cari akar – akar penyelesaian dari persamaan non linear dibawah ini dengan metode biseksi : a. X 3 – X 2 - X + 1 b. X 3 – 9 X 2 + 18 X – 6 = 0 c. X 6 – X – 1 = 0 n