PERAMALAN DENGAN TREND Trend adalah ratarata perubahan dalam

PERAMALAN DENGAN TREND Trend adalah rata-rata perubahan dalam jangka panjang (biasanya tiap tahun) Trend dapat berupa trend naik yang disebut trend positif dan dapat pula berupa trend turun yang disebut trend negatif Disebut trend positif apabila variabel yang diteliti (Y) menunjukkan gejala kenaikan atau menunjukkan rata-rata pertambahan Disebut trend negatif apabila variabel yang diteliti (Y) menunjukkan gejala semakin menurun atau menunjukkan rata-rata penurunan Trend dapat berupa trend linear, trend parabola/kwadratik, dan trend eksponensial 1

Untuk menghitung trend ada 4 metode : Free hands method (metode tangan bebas) Semi averages method (metode setengah rata-rata) Moving averages method (metode rata-rata bergerak) Least square method (metode kwadrat terkecil) 2

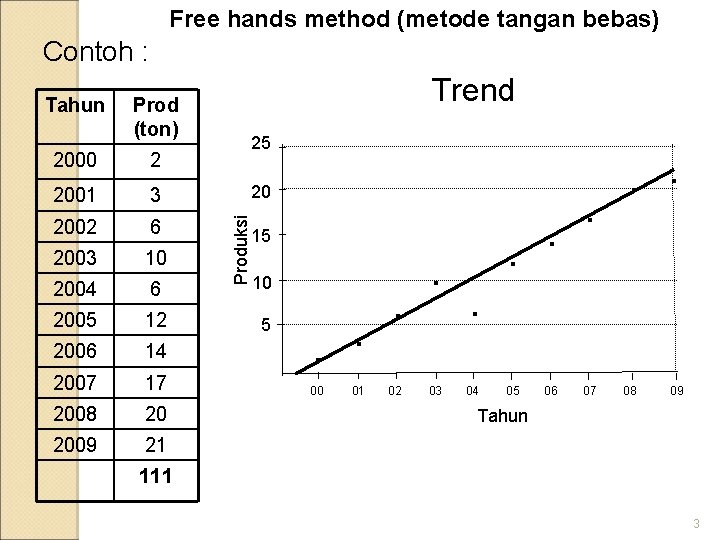
Free hands method (metode tangan bebas) Contoh : Trend Prod (ton) 2000 2 2001 3 2002 6 2003 10 2004 6 2005 12 2006 14 2007 17 2008 20 2009 21 25 20 Produksi Tahun 15 10 5 . . 00 01 . 02 . 03 . . . 04 05 06 07 08 09 Tahun 111 3

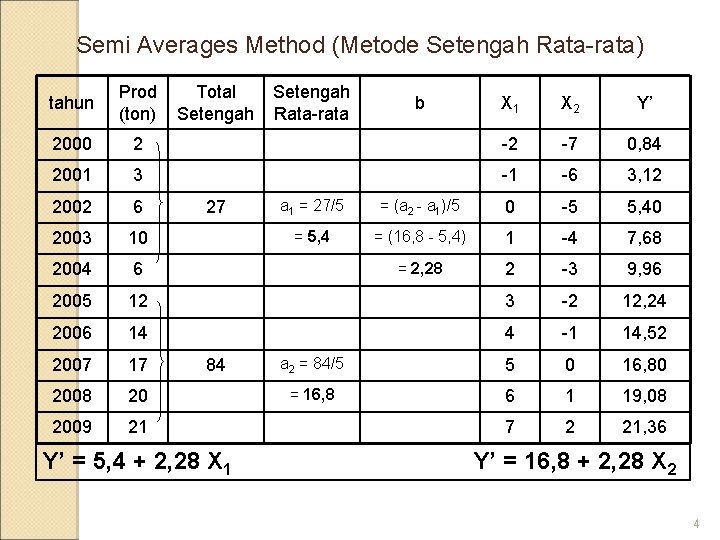
Semi Averages Method (Metode Setengah Rata-rata) tahun Prod Total (ton) Setengah Rata-rata b X 1 X 2 Y’ 2000 2 -2 -7 0, 84 2001 3 -1 -6 3, 12 2002 6 2003 10 2004 6 2005 a 1 = 27/5 = (a 2 - a 1)/5 0 -5 5, 40 = 5, 4 = (16, 8 - 5, 4) 1 -4 7, 68 = 2, 28 2 -3 9, 96 12 3 -2 12, 24 2006 14 4 -1 14, 52 2007 17 a 2 = 84/5 5 0 16, 80 2008 20 = 16, 8 6 1 19, 08 2009 21 7 2 21, 36 27 84 Y’ = 5, 4 + 2, 28 X 1 Y’ = 16, 8 + 2, 28 X 2 4

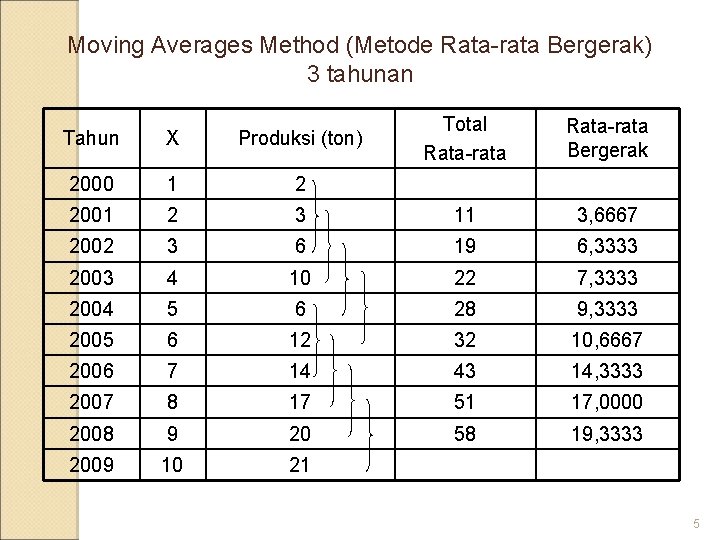
Moving Averages Method (Metode Rata-rata Bergerak) 3 tahunan Total Rata-rata Bergerak Tahun X Produksi (ton) 2000 1 2 2001 2 3 11 3, 6667 2002 3 6 19 6, 3333 2003 4 10 22 7, 3333 2004 5 6 28 9, 3333 2005 6 12 32 10, 6667 2006 7 14 43 14, 3333 2007 8 17 51 17, 0000 2008 9 20 58 19, 3333 2009 10 21 5

TREND LINEAR dengan Metode Kwadrat Terkecil Trend linear adalah trend dengan menggunakan persamaan garis lurus: Y = a + b. X Trend naik Trend turun 6

Trend Linier… Formulasi: Ŷ= a+bx Ŷ = Y cap= nilai trend (forecast) a = konstanta b = slope/kecondongan x = waktu (tahun) 7

Rumus 1: Y = n a + b X XY = a X + b X 2 8

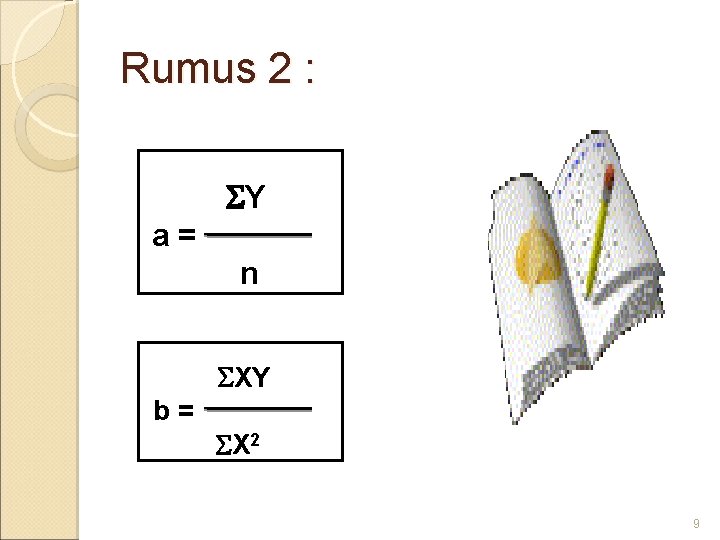
Rumus 2 : Y a= n XY b= X 2 9

Contoh: Suatu perusahaan mempunyai volume permintaan sebagai berikut: Tahun Y(jutaan Rp) X XY X 2 2003 2004 2005 2006 2007 2008 2009 110 112 125 135 140 145 150 -3 -2 -1 0 1 2 3 -330 -224 -125 0 140 290 450 9 4 1 0 1 4 9 ∑ 917 0 201 28 10

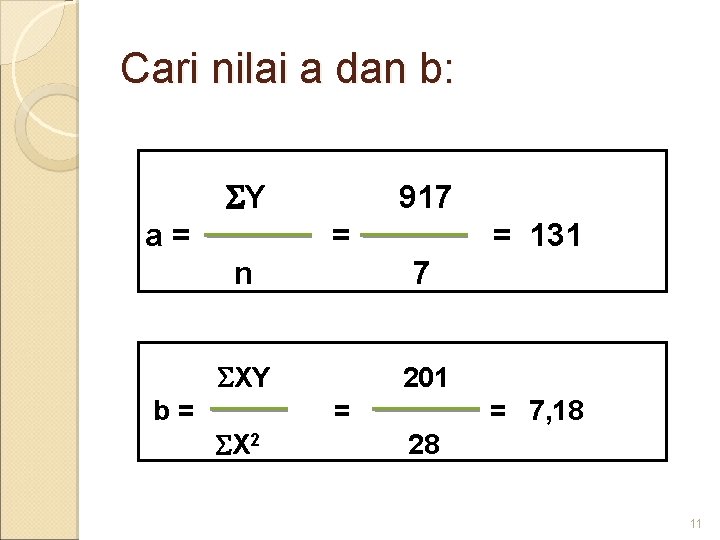
Cari nilai a dan b: Y a= 917 = = 131 n 7 XY 201 b= X 2 = = 7, 18 28 11

Jadi, persamaan trend: Y’ = 131 + 7, 18 X Peramalan penjualan tahun 2010: Y’ = 131 + 7, 18 X Y’ = 131 + 7, 18 (4) = 159, 72 Peramalan penjualan tahun 2011: Y’ = 131 + 7, 18 X Y’ = 131 + 7, 18 (5) = 166, 9 12

Contoh soal: Data produksi PT Prima Lestari 10 tahun terakhir sejak tahun 2001 sebagai berikut: 2, 3, 6, 8, 10, 12 , 14, 17, 20 dan 21 a. Tentukan persamaan garis trendnya? b. Tentukan peramalan tahun 2011 dan 2012 ? 13

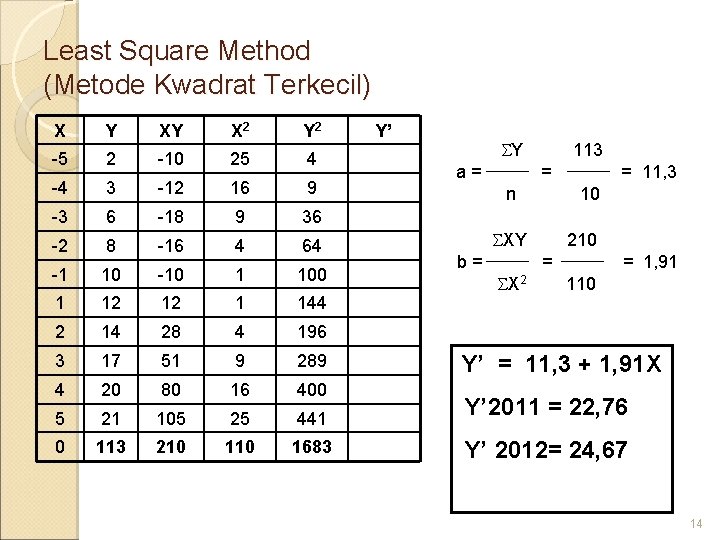
Least Square Method (Metode Kwadrat Terkecil) X Y XY X 2 Y’ -5 2 -10 25 4 -4 3 -12 16 9 -3 6 -18 9 36 -2 8 -16 4 64 -1 10 -10 1 100 1 12 12 1 144 2 14 28 4 196 3 17 51 9 289 4 20 80 16 400 5 21 105 25 441 Y’ 2011 = 22, 76 0 113 210 1683 Y’ 2012= 24, 67 Y 113 a = = 11, 3 n 10 XY 210 b = = 1, 91 X 2 110 Y’ = 11, 3 + 1, 91 X 14

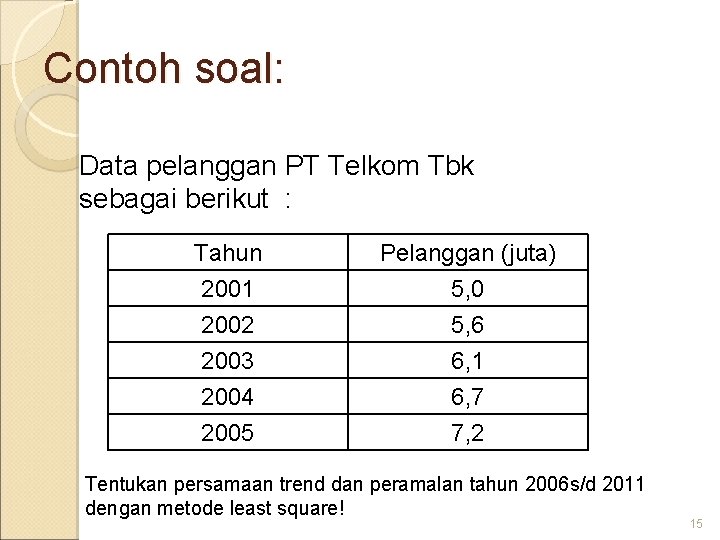
Contoh soal: Data pelanggan PT Telkom Tbk sebagai berikut : Tahun 2001 2002 2003 Pelanggan (juta) 5, 0 5, 6 6, 1 2004 2005 6, 7 7, 2 Tentukan persamaan trend dan peramalan tahun 2006 s/d 2011 dengan metode least square! 15

Lanjutan………………. . Tahun Kode X (tahun) -2 Y. X X 2 1997 Pelanggan =Y 5, 0 -10, 0 4 1998 5, 6 -1 -5, 6 1 1999 6, 1 0 0 0 2000 6, 7 1 2001 7, 2 2 14, 4 4 Y=30, 6 Y. X=5, 5 X 2=10 Nilai a = 30, 6/5=6, 12 Nilai b =5, 5/10=0, 55 Jadi persamaan trend Y’=6, 12+0, 55 x 16

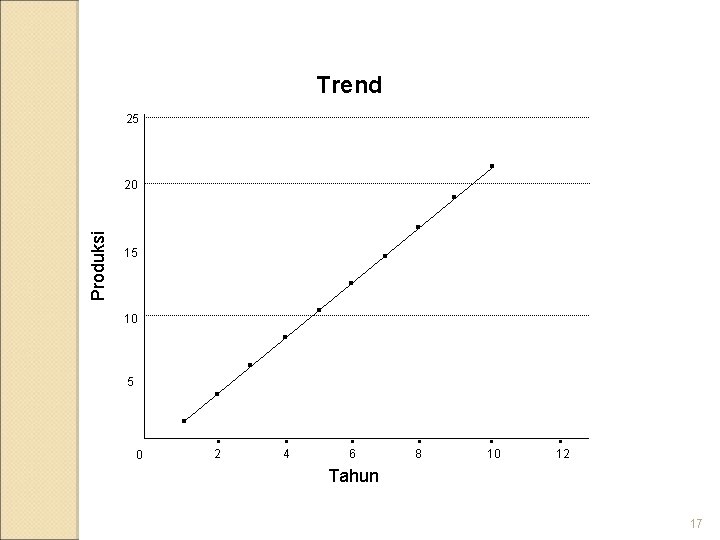
Trend 25 Produksi 20 15 10 5 . 0 . . 2 . . . 4 . . 6 . . 8 . . . 10 . 12 Tahun 17

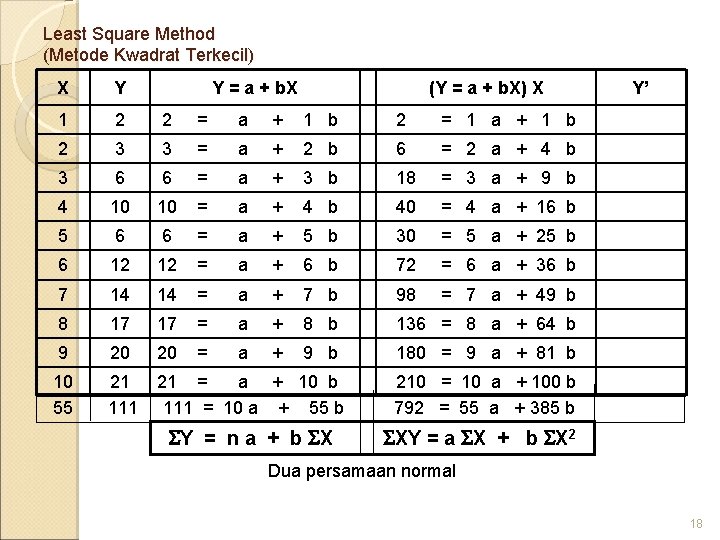
Least Square Method (Metode Kwadrat Terkecil) X Y Y = a + b. X (Y = a + b. X) X 1 2 2 = a + 1 b 2 = 1 a + 1 b 2 3 3 = a + 2 b 6 = 2 a + 4 b 3 6 6 = a + 3 b 18 = 3 a + 9 b 4 10 10 = a + 4 b 40 = 4 a + 16 b 5 6 6 = a + 5 b 30 = 5 a + 25 b 6 12 12 = a + 6 b 72 = 6 a + 36 b 7 14 14 = a + 7 b 98 = 7 a + 49 b 8 17 17 = a + 8 b 136 = 8 a + 64 b 9 20 20 = a + 9 b 180 = 9 a + 81 b Y’ 10 21 21 = a + 10 b 210 = 10 a + 100 b 55 111 = 10 a + 55 b 792 = 55 a + 385 b Y = n a + b X XY = a X + b X 2 Dua persamaan normal 18

Y = n a + b X XY = a X + b X 2 111 = 10 a + 55 b 55 6105 = 550 a + 3025 b 792 = 55 a + 385 b 10 7920 = 550 a + 3850 b 111 = 10 a + 55 b 111 = 10 a + 55 (2, 2) 111 = 10 a + 121 10 a = -1 1815 = 825 b b = 1815/825 b = 2, 2 Y’ = -1 + 2, 2 X 19

Deret Berkala dan Peramalan Bab 6 METODE ANALISIS TREND 2. Metode Kuadrat Terkecil Menentukan garis trend yang mempunyai jumlah terkecil dari kuadrat selisih data asli dengan data pada garis trendnya. Y = a + b. X a = Y/N b = YX/X 2 20

21

METODE ANALISIS TREND: Trend Non Linier TREND KUADRATIK Merupakan trend yang nilai variabel tak bebasnya naik atau turun secara linier atau terjadi parabola bila datanya dibuat scatter plot (hubungan variabel dependen dan independen adalah kuadratik) dan merupakan metode trend non linier. 22

Bentuk kurva trend kuadratik: 23

Formulasi trend kuadratik: Ŷ = a + b. X + c. X 2 Ŷ = Nilai trend yang diproyeksikan a, b, c = konstanta (nilai koefisien) X = waktu (tahun) 24

Lanjutan……. . Untuk melakukan suatu peramalan dengan metode trend kuadratik, maka kita harus mencari nilai konstanta a, b dan c terlebih dahulu dengan menggunakan rumus sebagai berikut: 25

Rumus 1: Dengan menggunakan rumus tiga persamaan normal: Y = n. a + b X + c X 2 XY = a X + b X 2 + c X 3 X 2 Y)= a X 2 + b X 3 + c X 4 Jika menggunakan x dengan skala angka (…-3, -2, -1, 0, 1, 2, 3…) baik pada data ganjil maupun genap maka, X dan X 3 = 0, 26

Lanjutan…. . sehingga persamaan diatas dapat disederhanakan menjadi: Y = n. a + c X 2 XY = b X 2 Y= a X 2 + c X 4 27

Rumus 2: ( Y) ( X 4) – ( X 2 Y) ( X 2) a = n ( X 4) - ( X 2)2 b = XY/ X 2 c = n( X 2 Y) – ( X 2 ) ( Y)/ n ( X 4) - ( X 2)2 28

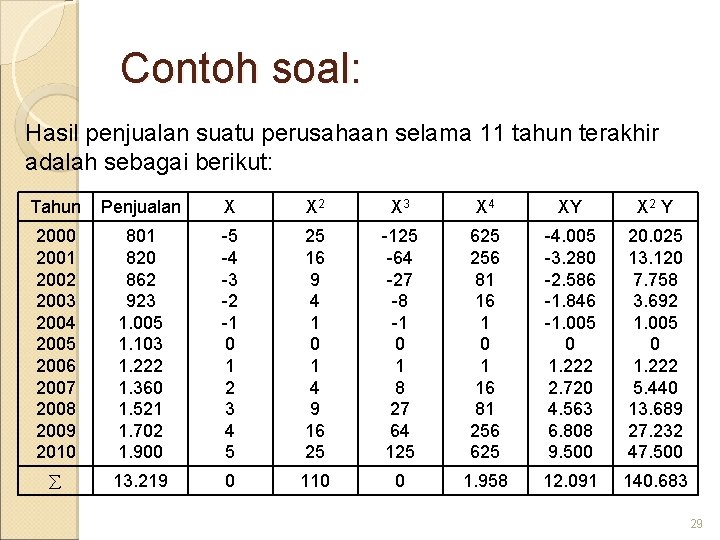
Contoh soal: Hasil penjualan suatu perusahaan selama 11 tahun terakhir adalah sebagai berikut: Tahun Penjualan X X 2 X 3 X 4 XY X 2 Y 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 801 820 862 923 1. 005 1. 103 1. 222 1. 360 1. 521 1. 702 1. 900 -5 -4 -3 -2 -1 0 1 2 3 4 5 25 16 9 4 1 0 1 4 9 16 25 -125 -64 -27 -8 -1 0 1 8 27 64 125 625 256 81 16 1 0 1 16 81 256 625 -4. 005 -3. 280 -2. 586 -1. 846 -1. 005 0 1. 222 2. 720 4. 563 6. 808 9. 500 20. 025 13. 120 7. 758 3. 692 1. 005 0 1. 222 5. 440 13. 689 27. 232 47. 500 13. 219 0 110 0 1. 958 12. 091 140. 683 29

Next……. . n= ganjil……… 2005; X=0 Persamaan normal: 1. Y = n. a + c X 2 13. 219= 11 a + 110 c 2. XY = b X 2 12. 091=110 b b= 109, 92 3. X 2 Y= a X 2 + c X 4 140. 683= 110 a + 1. 958 c 30

Dari persamaan 1 dan 3 13. 219 = 11 a + 110 c x 10 132. 190 = 110 a + 1. 100 c 140. 683 = 110 a + 1958 c 140. 683 = 110 a + 1. 958 c - 8. 493 = -858 c Dari persamaan 1 = c = 9, 90 13. 219 = 11 a + 110 c 13. 219 = 11 a + 110 (9, 90) 11 a = 13. 219 - 1. 089 11 a = 12. 130 a = 1. 102, 73 Jadi, persamaan forecastnya= Ŷ = 1. 102, 73 + 109, 92 X + 9, 90 X 2 31

Next……. . x= 6 Ŷ 20 I 1 = 1. 102, 73 + 109, 92(6) + 9, 90(62) = 1. 102, 73 + 659, 52 + 356, 4 = 2. 118, 65 32

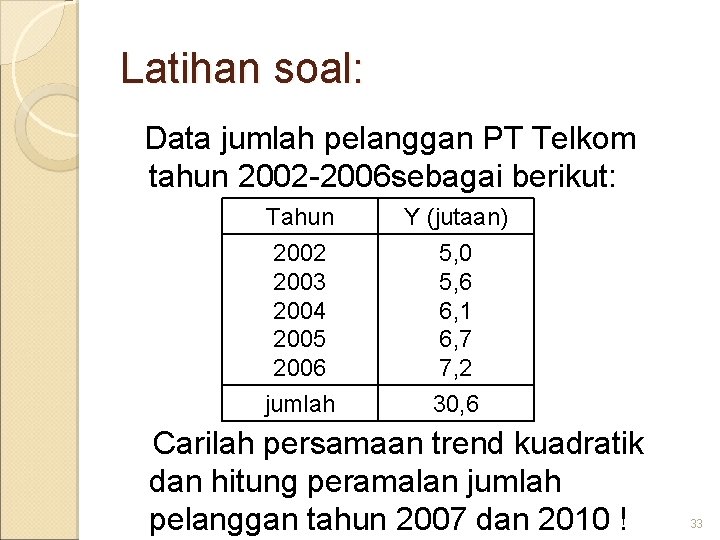
Latihan soal: Data jumlah pelanggan PT Telkom tahun 2002 -2006 sebagai berikut: Tahun 2002 2003 2004 2005 2006 jumlah Y (jutaan) 5, 0 5, 6 6, 1 6, 7 7, 2 30, 6 Carilah persamaan trend kuadratik dan hitung peramalan jumlah pelanggan tahun 2007 dan 2010 ! 33

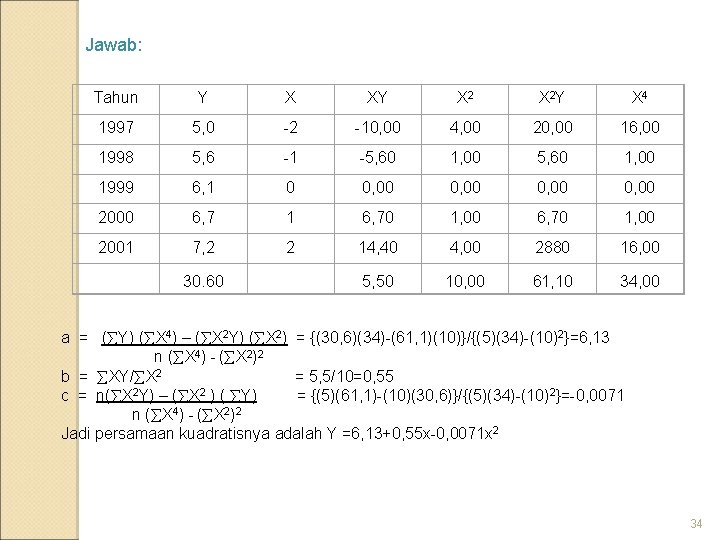
Jawab: Tahun Y X XY X 2 Y X 4 1997 5, 0 -2 -10, 00 4, 00 20, 00 16, 00 1998 5, 6 -1 -5, 60 1, 00 1999 6, 1 0 0, 00 2000 6, 7 1 6, 70 1, 00 2001 7, 2 14, 40 4, 00 2880 16, 00 2 30. 60 5, 50 10, 00 61, 10 34, 00 a = ( Y) ( X 4) – ( X 2 Y) ( X 2) = {(30, 6)(34)-(61, 1)(10)}/{(5)(34)-(10)2}=6, 13 n ( X 4) - ( X 2)2 b = XY/ X 2 = 5, 5/10=0, 55 c = n( X 2 Y) – ( X 2 ) ( Y) = {(5)(61, 1)-(10)(30, 6)}/{(5)(34)-(10)2}=-0, 0071 n ( X 4) - ( X 2)2 Jadi persamaan kuadratisnya adalah Y =6, 13+0, 55 x-0, 0071 x 2 34

Trend Non Linier : Trend Eksponensial Adalah suatu tren yang mempunyai pangkat atau eksponen dari waktunya. Bentuk persamaan eksponensial dirumuskan sebagai berikut: Y’ = a (1 + b)X Y’ = a. b. X 35

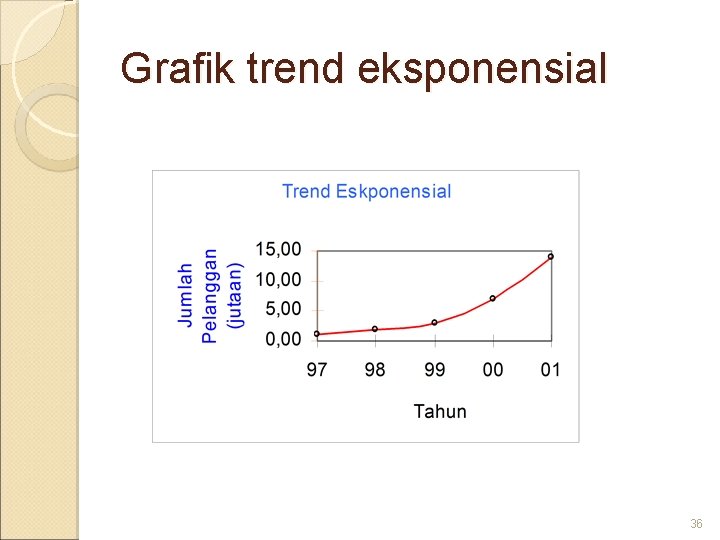
Grafik trend eksponensial 36

Rumus 1: Log Ŷ = log a + x log b log Y Log a = n (x. log Y) Log b = X 2 37

Rumus 2: Y’ = a (1 + b)X Ln Y’ = Ln a + X Ln (1+b) Sehingga a = anti ln ( Ln. Y)/n b = anti ln (X. Ln. Y) - 1 X 2 38

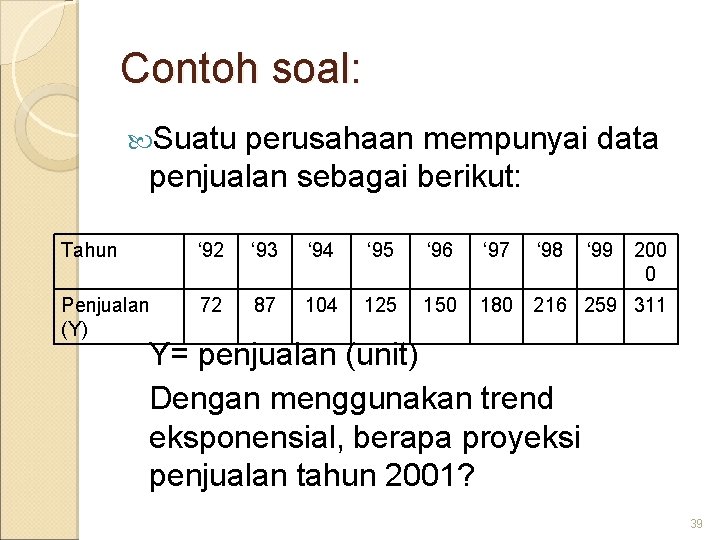
Contoh soal: Suatu perusahaan mempunyai data penjualan sebagai berikut: Tahun ‘ 92 ‘ 93 ‘ 94 ‘ 95 ‘ 96 ‘ 97 ‘ 98 ‘ 99 200 0 Penjualan (Y) 72 87 104 125 150 180 216 259 311 Y= penjualan (unit) Dengan menggunakan trend eksponensial, berapa proyeksi penjualan tahun 2001? 39

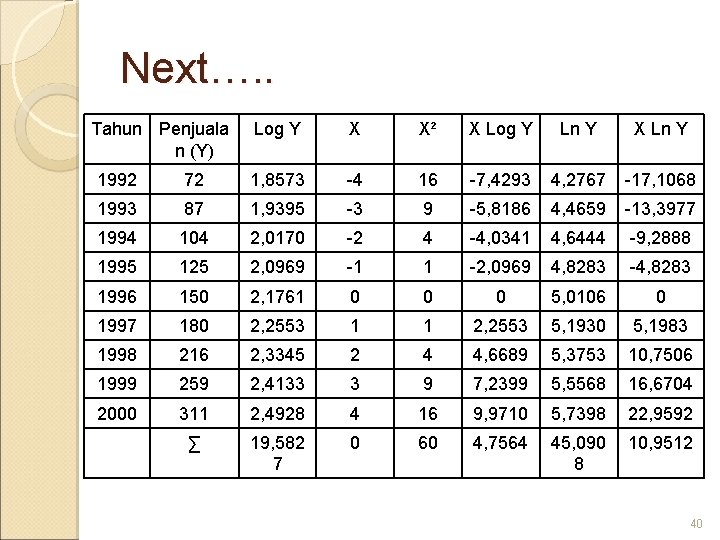
Next…. . Tahun Penjuala n (Y) Log Y X X² X Log Y Ln Y X Ln Y 1992 72 1, 8573 -4 16 -7, 4293 4, 2767 -17, 1068 1993 87 1, 9395 -3 9 -5, 8186 4, 4659 -13, 3977 1994 104 2, 0170 -2 4 -4, 0341 4, 6444 -9, 2888 1995 125 2, 0969 -1 1 -2, 0969 4, 8283 -4, 8283 1996 150 2, 1761 0 0 0 5, 0106 0 1997 180 2, 2553 1 1 2, 2553 5, 1930 5, 1983 1998 216 2, 3345 2 4 4, 6689 5, 3753 10, 7506 1999 259 2, 4133 3 9 7, 2399 5, 5568 16, 6704 2000 311 2, 4928 4 16 9, 9710 5, 7398 22, 9592 ∑ 19, 582 7 0 60 4, 7564 45, 090 8 10, 9512 40

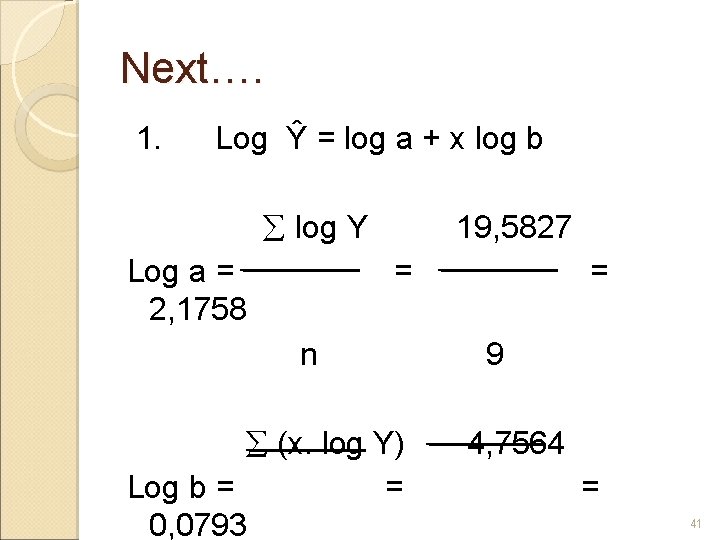
Next…. 1. Log Ŷ = log a + x log b log Y 19, 5827 Log a = = 2, 1758 n 9 (x. log Y) 4, 7564 Log b = = 0, 0793 41

Next……. . Jadi persamaan eksponensial: Log Ŷ = log a + x log b Log Ŷ = 2, 1758 + 0, 0793 x Peramalan Tahun 2001; x= 5 Log Ŷ 2001 = 2, 1758 + 0, 0793(5) = 2, 5723 Ŷ 2001 = 373, 51. 42

Next…. 2. Y’ = a (1 + b)X Ln Y’ = Ln a + X Ln (1+b) Sehingga a = anti ln ( Ln. Y)/n a = anti ln (45, 0908)/9 a = anti ln 5, 0101 a = 149, 9197 43

Next………. . b = anti ln (X. Ln. Y) - 1 X 2 b = anti ln 10, 9512 - 1 60 b = anti ln 0, 1825 - 1 b = 1, 2002 – 1 = 0, 2002 Jadi, persamaannya Y’ = a (1 + b)X Y’ = 149, 9197 (1 + 0, 2002)X Y’ = 149, 9197. 1, 2002 X Y’ 2001 = 149, 9197. 1, 20025 Y’ 2001 = 149, 9197. 2, 4904 Y’ 2001 = 373, 36 44

Contoh soal: Volume penjualan PT XYZ selama 5 tahun sejak tahun 2003 adalah 5, 5, 6, 1, 6, 7, dan 7, 2 Tentukan persamaan trend eksponensialnya dan berapa forecast tahun 2008 -2011? 45

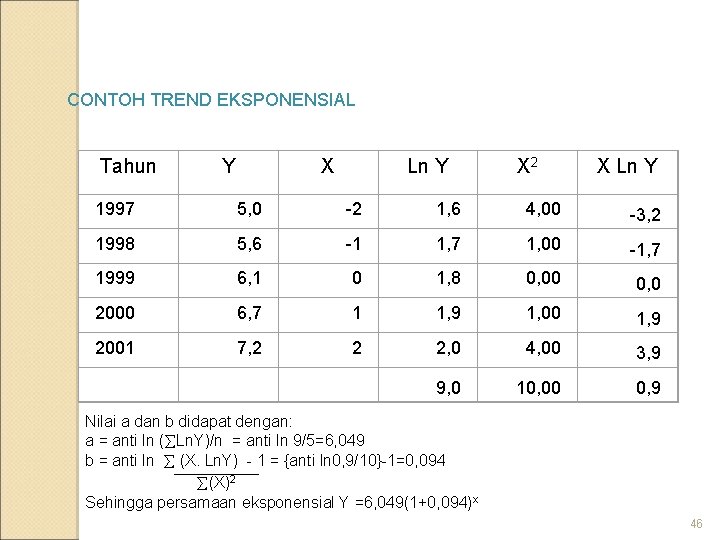
CONTOH TREND EKSPONENSIAL Tahun Y X Ln Y X 2 X Ln Y 1997 5, 0 -2 1, 6 4, 00 -3, 2 1998 5, 6 -1 1, 7 1, 00 -1, 7 1999 6, 1 0 1, 8 0, 00 0, 0 2000 6, 7 1 1, 9 1, 00 1, 9 2001 7, 2 2 2, 0 4, 00 3, 9 9, 0 10, 00 0, 9 Nilai a dan b didapat dengan: a = anti ln ( Ln. Y)/n = anti ln 9/5=6, 049 b = anti ln (X. Ln. Y) - 1 = {anti ln 0, 9/10}-1=0, 094 (X)2 Sehingga persamaan eksponensial Y =6, 049(1+0, 094)x 46