ENERGY CONVERSION ES 832 a Eric Savory www


























































































































- Slides: 159

ENERGY CONVERSION ES 832 a Eric Savory www. eng. uwo. ca/people/esavory/es 832. htm Lecture 14 – Wind Energy Part 2: Wind turbines Department of Mechanical and Material Engineering University of Western Ontario

Contents Modern wind turbines and their key components Basic operation of a Horizontal Axis Wind Turbine (HAWT) Estimation of the wind resource Statistical analysis of wind data and its use to predict available power (using Rayleigh and Weibull distributions) 1 -D momentum theory applied to an actuator disk model of the turbine, and the Betz limit Incorporation of wake rotation into the analysis Airfoil aerodynamics and blade design using momentum equation and blade element theory Blade optimization

Modern wind turbines In contrast to a windmill, which converts wind power into mechanical power, a wind turbine converts wind power into electricity. As an electricity generator a wind turbine is connected to an electrical network: - Battery charging circuit - Residential scale power units - Isolated or island networks - Large utility grids Most are small (< 10 k. W) but the total generating capacity is mostly from 0. 5 - 2 MW machines.

Underlying features of conversion process Aerodynamic lift force on the blades net positive torque on a rotating shaft mechanical power electrical power in a generator. No energy is stored – output is inherently fluctuating with the wind variability (though can limit output below what wind could produce at any given time). Any system turbine is connected to must be able to handle this variability.

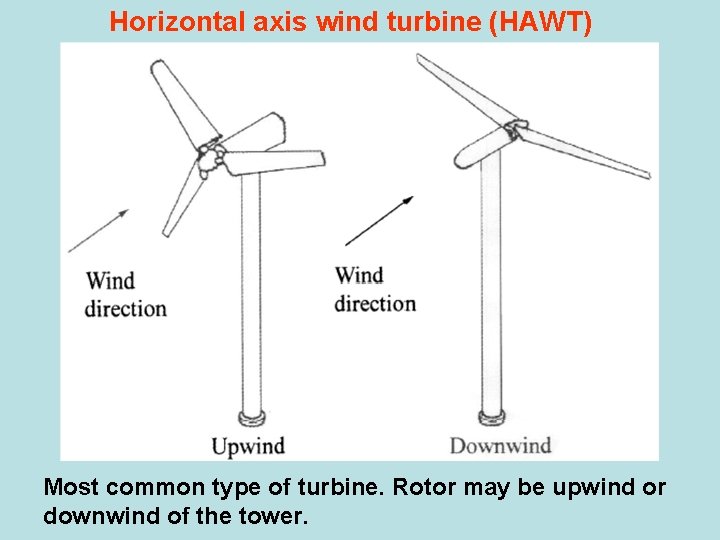
Horizontal axis wind turbine (HAWT) Most common type of turbine. Rotor may be upwind or downwind of the tower.

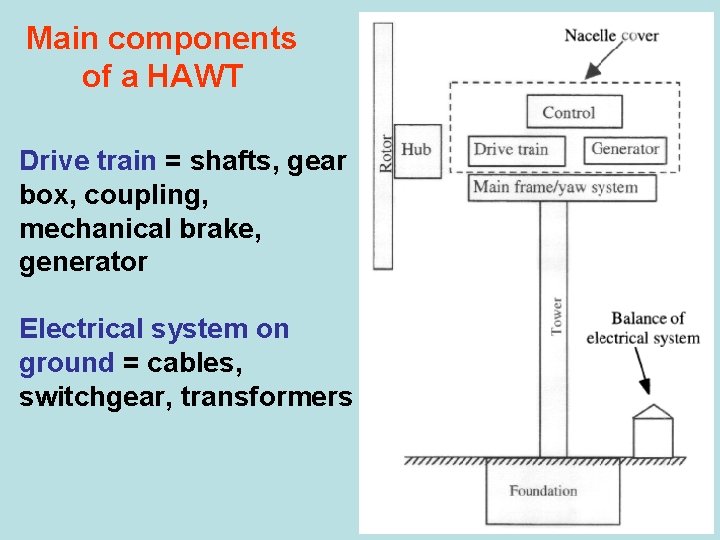
Main components of a HAWT Drive train = shafts, gear box, coupling, mechanical brake, generator Electrical system on ground = cables, switchgear, transformers

Main options in wind turbine design - Number of blades (commonly two or three) - Rotor orientation: downwind or upwind of tower - Blade material, construction method, and profile - Hub design: rigid, teetering or hinged - Power control via aerodynamic control (stall control) or variable pitch blades (pitch control) - Fixed or variable rotor speed - Orientation by self aligning action (free yaw), or direct control (active yaw) - Synchronous or induction generator - Gearbox or direct drive generator

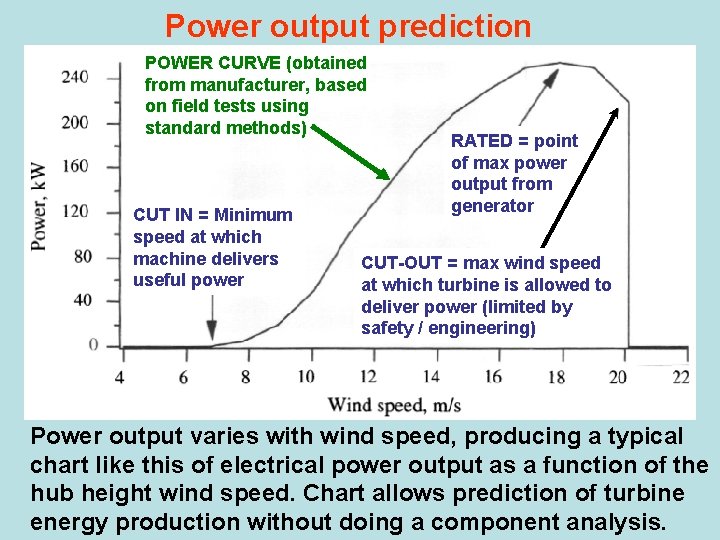
Power output prediction POWER CURVE (obtained from manufacturer, based on field tests using standard methods) CUT IN = Minimum speed at which machine delivers useful power RATED = point of max power output from generator CUT-OUT = max wind speed at which turbine is allowed to deliver power (limited by safety / engineering) Power output varies with wind speed, producing a typical chart like this of electrical power output as a function of the hub height wind speed. Chart allows prediction of turbine energy production without doing a component analysis.

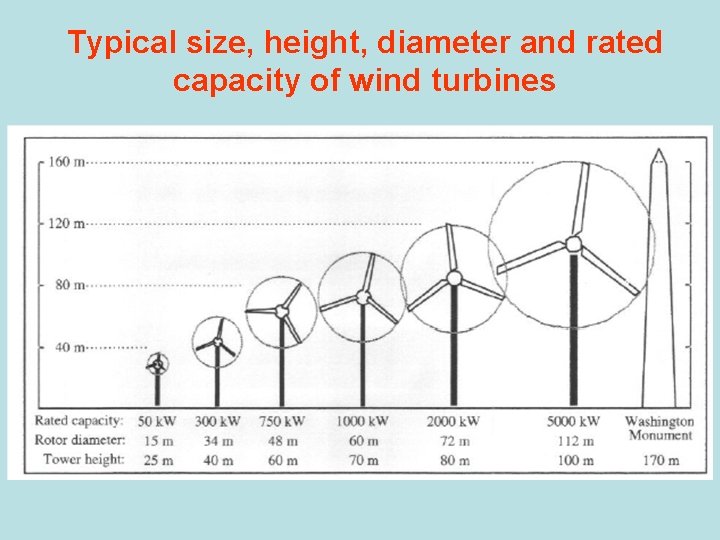
Typical size, height, diameter and rated capacity of wind turbines

Estimation of the potential wind resource The mass flow rate dm/dt of air of density and velocity U through a rotor disk of area A is: The kinetic energy per unit time, or power, of the flow is: The wind power per unit area, P/A or wind power density is: Note: density is generally taken as 1. 225 kg/m 3 (15 o. C at sea level). Actual power output is only about 45% of this available wind power for even the best turbines

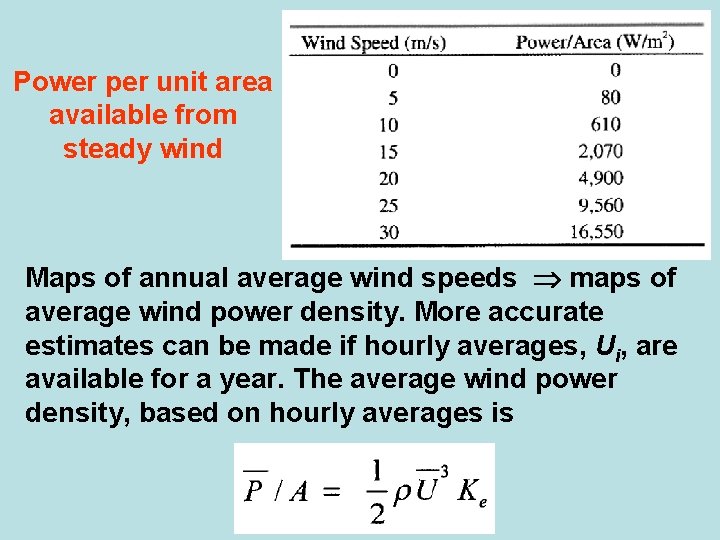
Power per unit area available from steady wind Maps of annual average wind speeds maps of average wind power density. More accurate estimates can be made if hourly averages, Ui, are available for a year. The average wind power density, based on hourly averages is

where U is the annual average wind speed and Ke is called the energy pattern factor. The energy pattern factor is calculated from: where N = number of hours in a year = 8, 760 Typical qualitative magnitude evaluations of the wind resource are: P / A < 100 W/m 2 - poor P / A ~ 400 W/m 2 - good P / A > 700 W/m 2 - great

Direct methods of data analysis, resource characterization, and turbine productivity Given a series of N wind speed observations, Ui, each averaged over the time interval t, we obtain: (1) The long-term average wind speed, U, over the total period of data collection: (2) The standard deviation U of the individual wind speed averages:

(3) The average wind power density P / A is Similarly, the wind energy density per unit area for a given extended time period T = N t is: (4) The average machine wind power Pw is: where Pw ( Ui ) is the power output defined by a wind machine power curve.

(5) The energy from a wind machine, Ew , is: = Method of bins The method of bins also provides a way to summarize wind data and to determine expected turbine productivity. The data must be separated into the wind speed intervals or bins in which they occur. It is convenient to use the same size bins. Suppose that the data are separated into NB bins of width wi with midpoints mj and with fj the number of occurrences in each bin or frequency, such that:

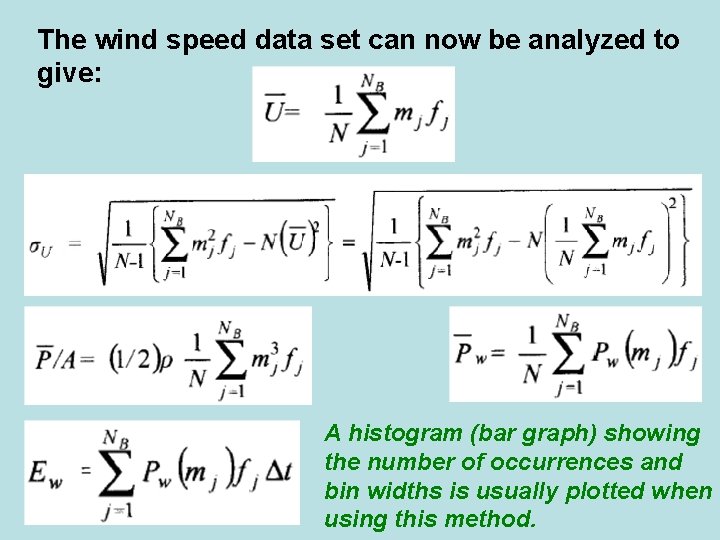
The wind speed data set can now be analyzed to give: A histogram (bar graph) showing the number of occurrences and bin widths is usually plotted when using this method.

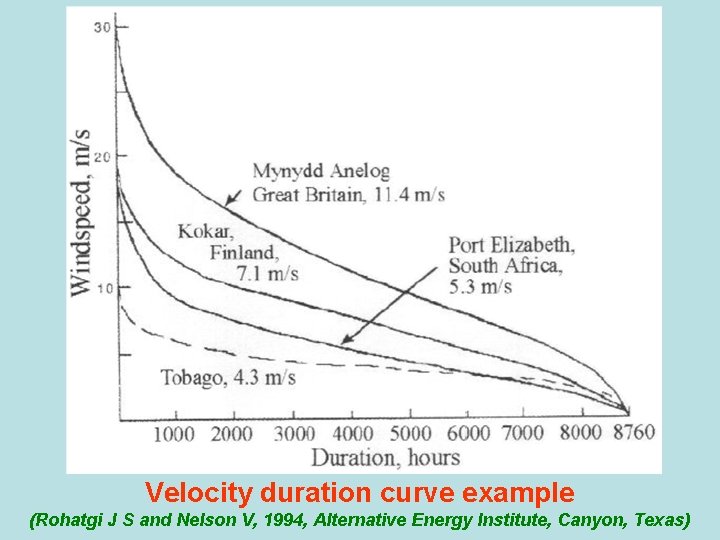
Velocity and power duration curves Can be useful when comparing the energy potential of candidate wind sites. The velocity duration curve is a graph with wind speed on the y axis and the number of hours in the year for which the speed equals or exceeds each particular value on the x axis. These plots give an indication of the nature of the wind regime at each site. The flatter the curve, the more constant are the wind speeds (e. g. characteristic of the trade-wind regions of the earth). The steeper the curve, the more irregular the wind regime.

Velocity duration curve example (Rohatgi J S and Nelson V, 1994, Alternative Energy Institute, Canyon, Texas)

A velocity duration curve can be converted to a power duration curve by cubing the ordinates, which are then proportional to the available wind power for a given rotor swept area. The difference between the energy potential of different sites is visually apparent, because the areas under the curves are proportional to the annual energy available from the wind. The following steps must be carried out to construct velocity and power duration curves from data: (1) Arrange the data in bins (2) Find the number of hours that a given velocity (or power per unit area) is exceeded (3) Plot the resulting curves

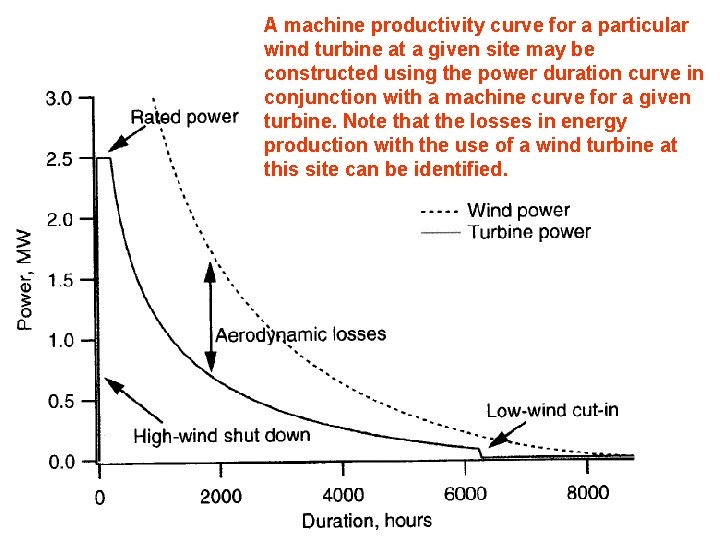
A machine productivity curve for a particular wind turbine at a given site may be constructed using the power duration curve in conjunction with a machine curve for a given turbine. Note that the losses in energy production with the use of a wind turbine at this site can be identified.

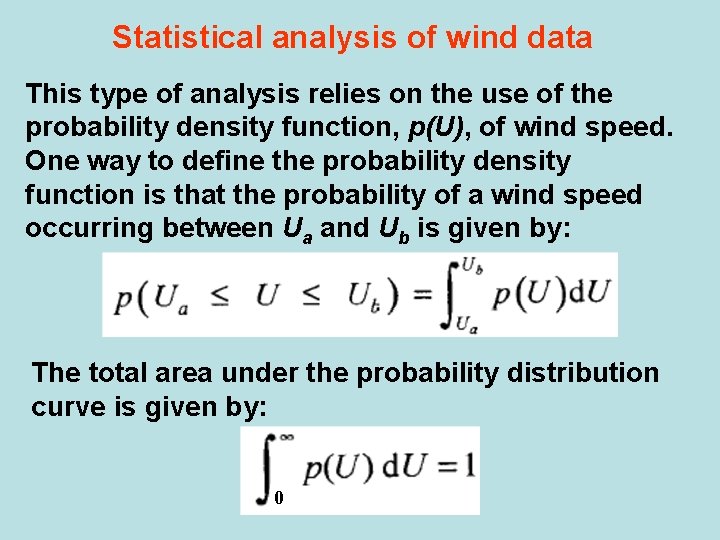
Statistical analysis of wind data This type of analysis relies on the use of the probability density function, p(U), of wind speed. One way to define the probability density function is that the probability of a wind speed occurring between Ua and Ub is given by: The total area under the probability distribution curve is given by: 0

If p(U) is known, the following parameters can be calculated: Mean wind speed, U 0 Standard deviation of wind speed, U Mean available wind power density, P / A 0 0 It should be noted that the probability density function can be superimposed on a wind velocity histogram by scaling it to the area of the histogram.

Another important statistical parameter is the cumulative distribution function F(U) which represents the time fraction or probability that the wind speed is smaller than or equal to a given wind speed, U'. That is: F(U) = Probability (U' U ) where U' is a dummy variable. It can be shown that: 0 Also, the slope of the cumulative distribution function is equal to the probability density function:

Probability density function equations In general, either one of two probability distributions (or probability density functions) are used in wind data analysis: (1) Rayleigh and (2) Weibull (see Lecture 13 notes) The Rayleigh distribution uses one parameter, the mean wind speed. The Weibull distribution is based on two parameters and, thus, can better represent a wider variety of wind regimes. Both are 'skew' distributions (defined only for values > 0).

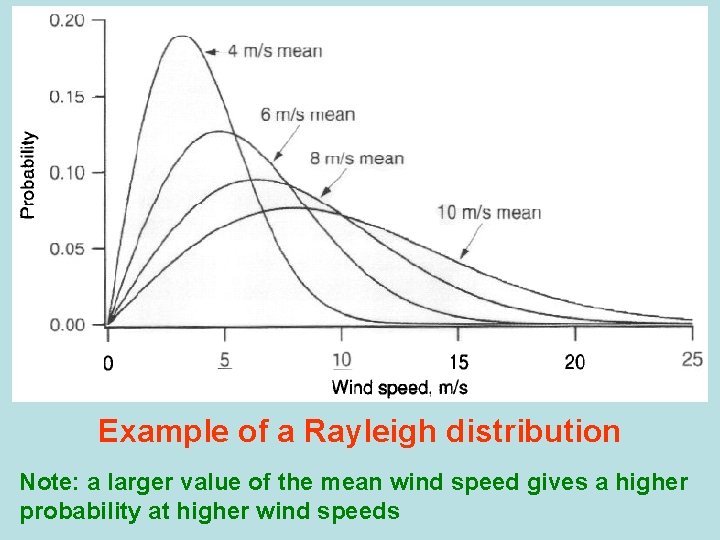
Rayleigh distribution Requires only a knowledge of the mean wind speed, U. The probability density function and the cumulative distribution function are given by:

Example of a Rayleigh distribution Note: a larger value of the mean wind speed gives a higher probability at higher wind speeds

Weibull distribution Determination of the Weibull probability density function requires a knowledge of two parameters: k, a shape factor and c, a scale factor. Both are a function of U and U. The Weibull probability density function and the cumulative distribution function may be given by: Note: methods for determining k and c from U and U are given in an appendix at the end of these notes

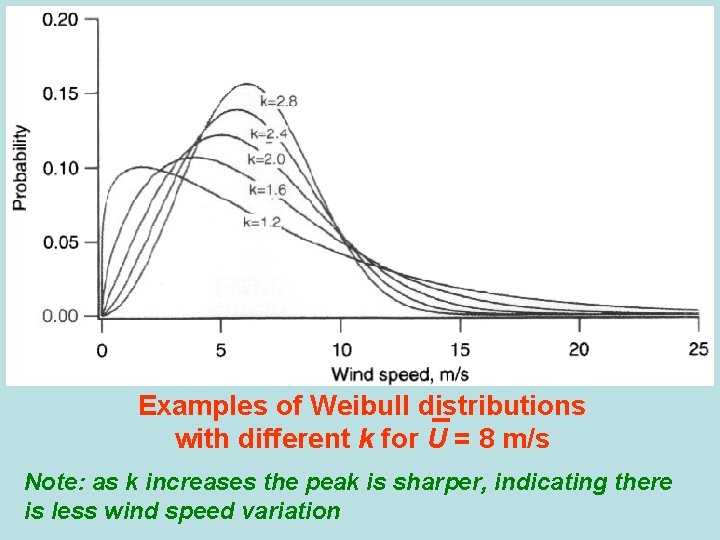
Examples of Weibull distributions with different k for U = 8 m/s Note: as k increases the peak is sharper, indicating there is less wind speed variation

Wind Turbine Energy Production Estimates Using Statistical Techniques For a given wind regime probability distribution p(U) and a known machine power curve Pw(U), the average wind machine power Pw is given by: Pw(U) may be determined from the wind power, the rotor power coefficient Cp and the drive train efficiency ( = generator power / rotor power):

where Cp is also a function of tip speed ratio defined as: where is the rotor angular velocity and R is rotor radius. Hence, assuming constant , average wind machine power is also given by

Idealized machine productivity calculations using Rayleigh distribution Assuming: (1) Idealized wind turbine, no losses, machine power coefficient, Cp , equal to the Betz limit (Cp, Betz = 16/27 = theoretical maximum possible power coefficient). (2) Wind speed probability distribution is given by a Rayleigh distribution. The average wind machine power equation becomes:

where Uc is a characteristic wind velocity given by For an ideal machine = 1, Cp = Cp, Betz = 16/27, so Using x = U / Uc gives a simpler integral Over all wind speeds, the integral becomes so that

Substituting for the rotor disk area, A = D 2/4, and for the characteristic velocity Uc the equation for average power becomes simply: Example: What is the average annual energy production of an 18 m diameter Rayleigh-Betz machine at sea level in a 6 m/s average annual wind velocity regime?

Solution: Pw Multiplying this by 8, 760 hrs/yr gives an expected annual energy production of 334, 000 k. Whr Comparing this result to the simple approach in Slide 10 where: P = ½ A U 3 = ½ (¼ D 2 ) U 3 = ( 0. 627 D) 2 U 3 shows that the simple method under-estimates the power by about 12%

Productivity calculations for a real wind turbine using a Weibull distribution The average wind machine power equation based upon the probability distribution function p(U) may be re-cast in terms of the cumulative distribution F(U): 0 (1) 0 The Weibull distribution is Therefore, using (2) in (1) and replacing the integral with a summation over NB bins gives (2)

Pw = Note: the above equation is the statistical method’s equivalent to the earlier equation: where the relative frequency f / N corresponds to the term in brackets and the wind turbine power is calculated at the mid-point between Uj - 1 and Uj

1 -D Momentum Theory and the Betz Limit A simple model may be used to determine the power from an ideal turbine rotor, the thrust of the wind on the ideal rotor and the effect of the rotor operation on the local wind field. The analysis assumes a control volume, in which the boundaries are the surface of a stream tube and two crosssections of the stream tube:

The only flow is across the ends of the stream tube. The turbine is represented by a uniform "actuator disk" which creates a discontinuity of pressure in the stream tube of air flowing through it. This approach is not limited to any particular type of wind turbine. The analysis uses the following assumptions: - Homogenous, incompressible, steady state flow - No frictional drag - An infinite number of blades - Uniform thrust over the disk or rotor area - A non-rotating wake - The static pressure far upstream and far downstream of the rotor is equal to the undisturbed ambient static pressure

The thrust T is equal to the change in momentum rate: But the mass flow rate is: So that: T is +ve so the velocity behind the rotor U 4 is less than the free stream velocity U 1. No work is done on either side of the turbine rotor. Thus, the Bernoulli equation can be used in the two control volumes on either side of the actuator disk.

Streamtube upstream of disk: Streamtube downstream of disk: It is assumed that the far upstream and far downstream pressures are equal ( p 1 = p 4 ) and that the velocity across the disk remains the same ( U 2 = U 3 ). The thrust can also be expressed as the net sum of the forces on each side of the actuator disc: 2

Using the Bernoulli equations to solve for ( p 2 - p 3 ) we obtain the thrust as: Equating this with our first two expressions for T and recognizing that the mass flow rate is A 2 U 2 we obtain for the wind velocity in the rotor plane simply: Defining the axial induction factor a as the fractional decrease in wind velocity between the free stream and the rotor plane: and

The quantity U 1 a is the “induced velocity” at the rotor, so the wind velocity there is a combination of the free stream velocity and the induced velocity. As the axial induction factor increases from 0, the wind speed behind the rotor reduces. If a = 1/2, the wind has slowed to zero velocity behind the rotor and this simple theory is no longer applicable. The power out P is equal to the thrust times the velocity at the disk: U 2

Substituting in the expressions for U 2 and U 4: gives: where A is the rotor area and U is the freestream velocity. The power coefficient CP represents the amount of available wind power extracted by the rotor:

The maximum value of CP occurs when a = 1/3 so that: CP, max = 16 / 27 = 0. 5926 For this case, the flow through the disk corresponds to a stream tube with an upstream cross-sectional area of 2/3 the disk area that expands to twice the disk area downstream. This result indicates that, if an ideal rotor were designed and operated such that the wind speed at the rotor were 2/3 of the freestream wind speed, then it would be operating at the point of maximum power production.

The thrust T and thrust coefficient CT can now be computed as Hence, the thrust coefficient for an ideal wind turbine is equal to 4 a (1 - a). CT has a maximum of 1. 0 when a = 0. 5 and the downstream velocity is zero. At maximum power output (a = 1/3), CT has a value of 8/9.

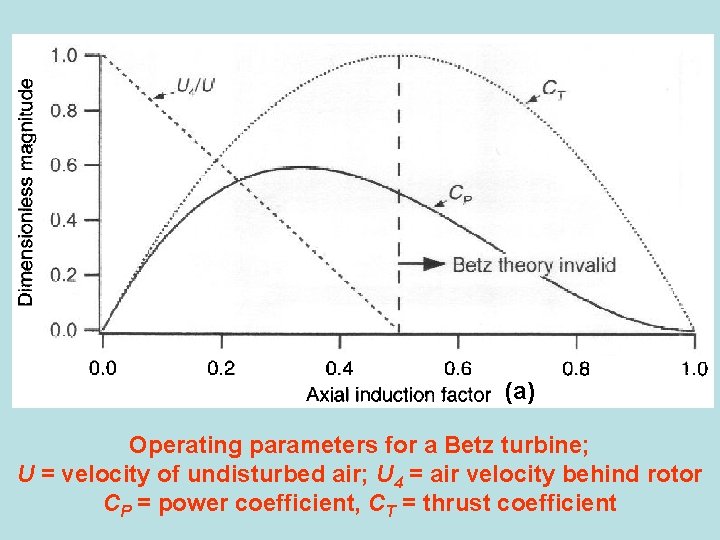
(a) Operating parameters for a Betz turbine; U = velocity of undisturbed air; U 4 = air velocity behind rotor CP = power coefficient, CT = thrust coefficient

The Betz limit, CP, max = 16/27, is the maximum theoretically possible rotor power coefficient. In practice 3 effects lead to a decrease in the maximum achievable power coefficient: - Rotation of the wake behind the rotor - Finite number of blades and their tip losses - Non-zero aerodynamic drag Note that the overall turbine efficiency is a function of both the rotor power coefficient and the mechanical (including electrical) efficiency of the wind turbine:

Ideal HAWT with Wake Rotation In reality the generation of rotational KE in the wake results in less energy extraction by the rotor than would be expected without wake rotation. In general, the extra KE in the wind turbine wake will be higher if the generated torque is higher. Thus, as will be shown here, slow running wind turbines (with a low rotational speed and a high torque) experience more wake rotation losses than high-speed wind machines with low torque.

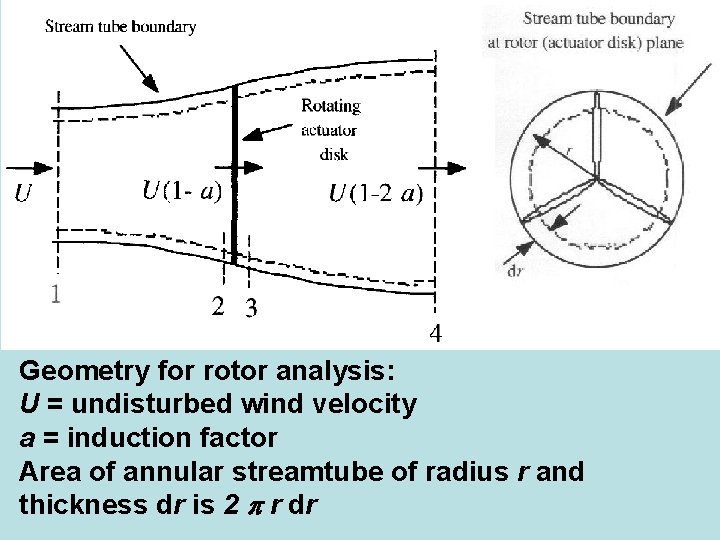
Geometry for rotor analysis: U = undisturbed wind velocity a = induction factor Area of annular streamtube of radius r and thickness dr is 2 r dr

Assuming angular velocity imparted to flow is small compared to angular velocity of the rotor pressure in far wake = pressure in freestream. The pressure, wake rotation and induction factors are all assumed to be a function of radial position r. Using a CV that moves with angular velocity the energy equations can be applied at sections before and after the blades to derive the pressure difference across them. Across the flow disk the angular velocity of the air relative to the blade increases from to + , whilst the axial component of the velocity remains constant.

We obtain: The resulting thrust on an annular element, d. T, is: The angular induction factor, a’ , is defined as: Note that when wake rotation is included in the analysis, the induced velocity at the rotor consists of not only the axial component, U a, but also a component in the rotor plane, r a'.

The expression for the thrust becomes: From our previous linear momentum analysis, the thrust on an annular cross-section can also be determined by the following expression that uses the axial induction factor, a : Equating these two thrust expressions gives: where r is the local speed ratio:

Next, we derive an expression for the torque on the rotor by applying the conservation of angular momentum. For this situation, the torque exerted on the rotor, Q, must equal the change in angular momentum of the wake. On an incremental annular area element this gives: Since U 2 = U (1 - a) and a' = / 2 , this expression reduces to: The power generated at each element, d. P, is given by:

Substituting for d. Q in this expression and using the definition of the local speed ratio, r , the expression for the power generated at each element becomes: It can be seen that the power from any annular ring is a function of the axial and angular induction factors and the tip speed ratio. The axial and angular induction factors determine the magnitude and direction of the airflow at the rotor plane. The local speed ratio is a function of the tip speed ratio and radius.

The incremental contribution to the power coefficient, d. CP, from each annular ring is given by: Now, a’ is related to a and r by:

The aerodynamic conditions for the maximum possible power production occur when the term a’ (1 - a) in the CP equation on the previous slide is at its greatest value. Substituting the value for a’ from the last equation into a’ (1 - a) and setting the derivative with respect to a equal to zero yields: This equation defines the axial induction factor for maximum power as a function of the local tip speed ratio in each annular ring.

Substituting into we finds that, for maximum power in each annular ring: If the equation is differentiated with respect to a, we obtain a relationship between d r and da at the condition for maximum power production:

Substituting the previous three equations into the expression for the power coefficient: gives: where the lower limit of integration a 1 corresponds to the axial induction factor for r = 0 and the upper limit a 2 corresponds to the axial induction factor at r = .

Also, from we have for a 2: and also r = 0 for a 1 = 0. 25. This equation for can be solved for the values of a 2 that correspond to tip speed ratios of interest, noting that a 2 = 1/3 is the upper limit of a, giving an infinitely large tip speed ratio. The integral for CP, max can be evaluated by changing of variables, substituting x for (1 - 3 a):

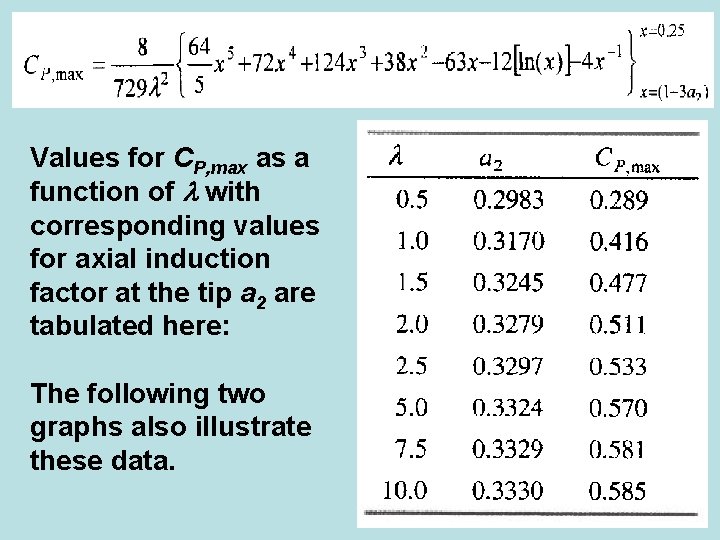
Values for CP, max as a function of with corresponding values for axial induction factor at the tip a 2 are tabulated here: The following two graphs also illustrate these data.

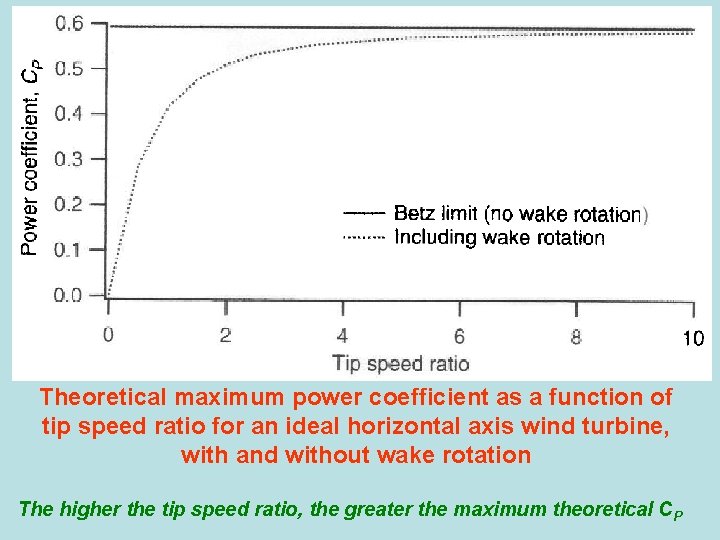
Theoretical maximum power coefficient as a function of tip speed ratio for an ideal horizontal axis wind turbine, with and without wake rotation The higher the tip speed ratio, the greater the maximum theoretical C P

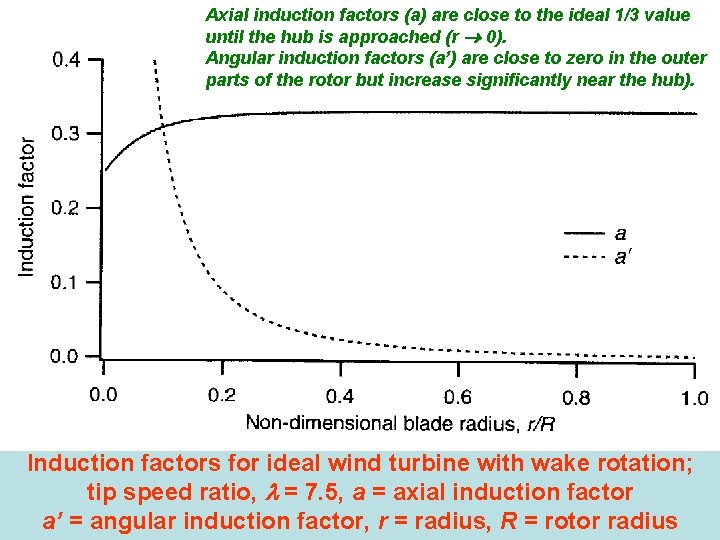
Axial induction factors (a) are close to the ideal 1/3 value until the hub is approached (r 0). Angular induction factors (a’) are close to zero in the outer parts of the rotor but increase significantly near the hub). Induction factors for ideal wind turbine with wake rotation; tip speed ratio, = 7. 5, a = axial induction factor a’ = angular induction factor, r = radius, R = rotor radius

Airfoils and general aerodynamic concepts Wind turbine blades use airfoil sections to develop mechanical power. The width and length of the blades are a function of the desired aerodynamic performance and the maximum desired rotor power (as well as strength considerations). Before examining the details of wind turbine power production, some airfoil aerodynamics principles are reviewed here.

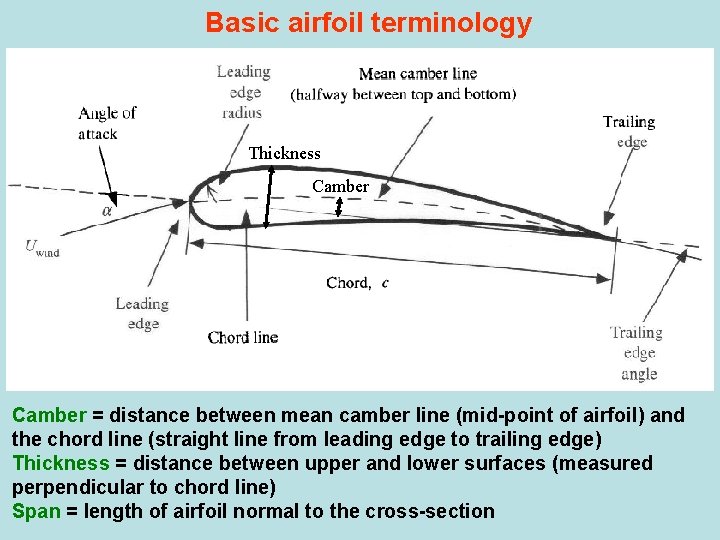
Basic airfoil terminology Thickness Camber = distance between mean camber line (mid-point of airfoil) and the chord line (straight line from leading edge to trailing edge) Thickness = distance between upper and lower surfaces (measured perpendicular to chord line) Span = length of airfoil normal to the cross-section

Examples of standard airfoil shapes NACA 0012 = 12% thick symmetric airfoil NACA 63(2)-215 = 15% thick airfoil with slight camber LS(1)-0417 = 17% thick airfoil with larger camber

Lift, drag and non-dimensional parameters Airflow over an airfoil produces a distribution of forces over the airfoil surface. The flow velocity over airfoils increases over the convex surface resulting in lower average pressure on the 'suction' side of the airfoil compared with the concave or 'pressure' side of the airfoil. Meanwhile, viscous friction between the air and the airfoil surface slows the airflow to some extent next to the surface.

Lift force - defined to be perpendicular to direction of the oncoming airflow. The lift force is a consequence of the unequal pressure on the upper and lower airfoil surfaces Drag force - defined to be parallel to the direction of oncoming airflow. The drag force is due both to viscous friction forces at the surface of the airfoil and to unequal pressure on the airfoil surfaces facing toward and away from the oncoming flow Pitching moment - defined to be about an axis perpendicular to the airfoil cross-section

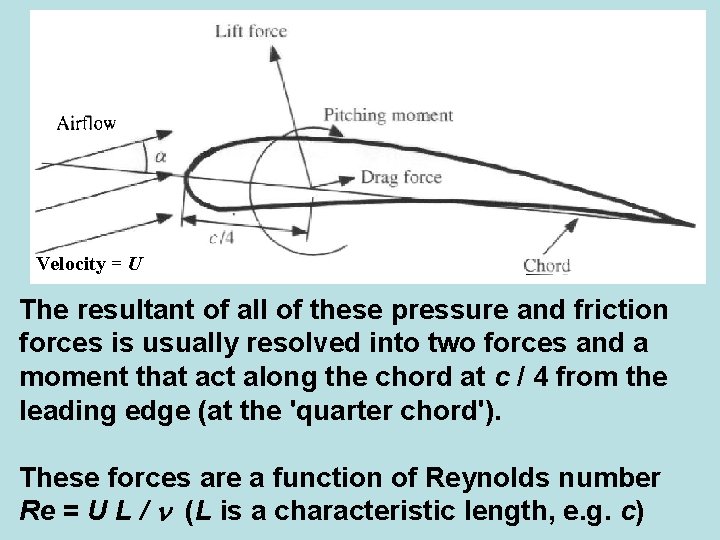
Velocity = U The resultant of all of these pressure and friction forces is usually resolved into two forces and a moment that act along the chord at c / 4 from the leading edge (at the 'quarter chord'). These forces are a function of Reynolds number Re = U L / (L is a characteristic length, e. g. c)

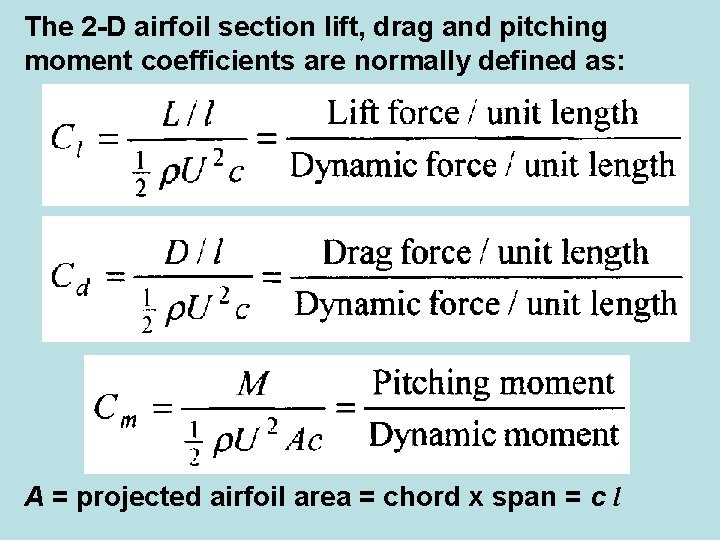
The 2 -D airfoil section lift, drag and pitching moment coefficients are normally defined as: A = projected airfoil area = chord x span = c l

Other dimensionless parameters that are important for analysis and design of wind turbines include the power and thrust coefficients and tip speed ratio, mentioned earlier and also the pressure coefficient: and blade surface roughness ratio:

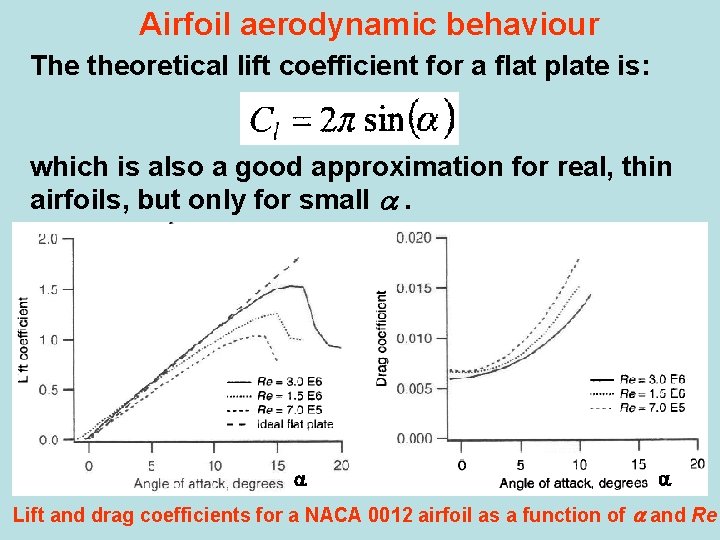
Airfoil aerodynamic behaviour The theoretical lift coefficient for a flat plate is: which is also a good approximation for real, thin airfoils, but only for small . Lift and drag coefficients for a NACA 0012 airfoil as a function of and Re

Airfoils for HAWT are often designed to be used at low angles of attack, where lift coefficients are fairly high and drag coefficients are fairly low. The lift coefficient of this symmetric airfoil is about zero at an angle of attack of zero and increases to over 1. 0 before decreasing at higher angles of attack. The drag coefficient is usually much lower than the lift coefficient at low angles of attack. It increases at higher angles of attack. Note the significant differences in airfoil behaviour at different Re. Rotor designers must make sure that appropriate Re data are available for analysis.

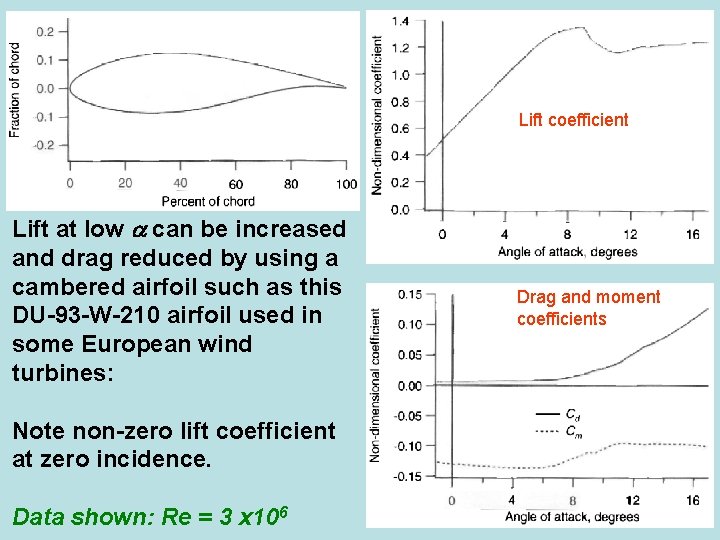
Lift coefficient Lift at low can be increased and drag reduced by using a cambered airfoil such as this DU-93 -W-210 airfoil used in some European wind turbines: Note non-zero lift coefficient at zero incidence. Data shown: Re = 3 x 106 Drag and moment coefficients

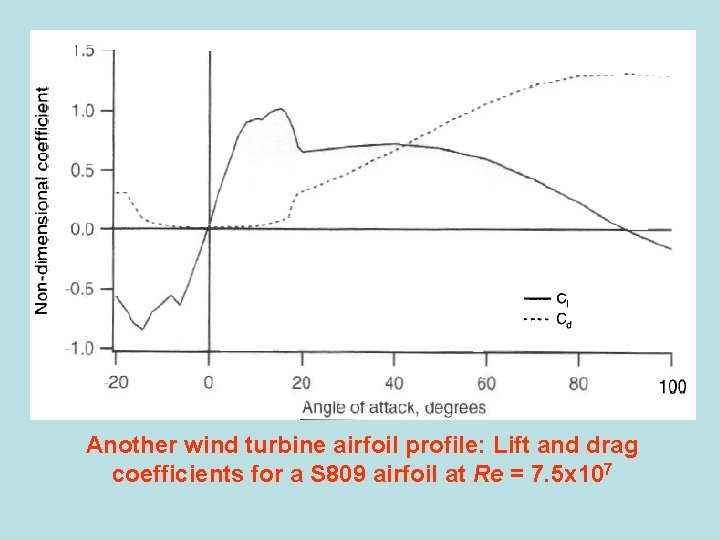
Another wind turbine airfoil profile: Lift and drag coefficients for a S 809 airfoil at Re = 7. 5 x 107

Attached flow regime: At low (up to about 7 o for DU-93 -W-210), flow is attached to upper surface of the airfoil. In this regime, lift increases with and drag is relatively low. High lift/stall development regime: Here (from about 7 -11 o for DU-93 -W-210), lift coeff peaks as airfoil becomes increasingly stalled. Stall occurs when exceeds a critical value (10 -16 o, depending on Re) and separation of the boundary layer on the upper surface occurs. This causes a wake above the airfoil, reducing lift and increasing drag. This can occur at certain blade locations or conditions of wind turbine operation. It is sometimes used to limit wind turbine power in high winds. For example, many designs using fixed pitch blades rely on power regulation control via aerodynamic stall of the blades. That is, as wind speed increases, stall progresses outboard along the span of the blade (toward the tip) causing decreased lift and increased drag. In a well designed, stall regulated machine, this results in nearly constant power output as wind speeds increase.

Flat plate/fully stalled regime: In the flat plate/fully stalled regime, at larger up to 90 o, the airfoil acts increasingly like a simple flat plate with approximately equal lift and drag coefficients at of 45 o and zero lift at 90 o. Illustration of airfoil stall

Airfoils for wind turbines Typical blade chord Re range is 5 x 105 – 1 x 107 1970 s and 1980 s – designers thought airfoil performance was less important than optimising blade twist and taper. Hence, helicopter blade sections, such as NACA 44 xx and NACA 230 xx, were popular as it was viewed as a similar application (high max. lift, low pitching moment, low min. drag). But the following shortcomings have led to more attention on improved airfoil design:

Operational experience showed shortcomings (e. g. stall controlled HAWT produced too much power in high winds, causing generator damage). Turbines were operating with some part of the blade in deep stall for more than 50% of the lifetime of the machine. Peak power and peak blade loads were occurring while turbine was operating with most of the blade stalled and predicted loads were 50 – 70% of the measured loads! Leading edge roughness affected rotor performance. Insects and dirt output dropped by up to 40% of clean value!

Momentum theory and Blade Element theory The actuator disk approach yields the pressure change across the disk that is, in practice, produced by blades. This, and the axial and angular induction factors that are a function of rotor power extraction and thrust, will now be used to define the flow at the airfoils. The rotor geometry and its associated lift and drag characteristics can then be used to determine - rotor shape if some performance parameters are known, or - rotor performance if the blade shape has been defined.

Analysis uses: Momentum theory - CV analysis of the forces at the blade based on the conservation of linear and angular momentum. Blade element theory – analysis of forces at a section of the blade, as a function of blade geometry. Results combined into “strip theory” or blade element momentum (BEM) theory. This relates blade shape to the rotor's ability to extract power from the wind.

Analysis encompasses: - Momentum and blade element theory. - The simplest 'optimum' blade design with an infinite number of blades and no wake rotation. - Performance characteristics (forces, rotor airflow characteristics, power coefficient) for a general blade design of known chord and twist distribution, including wake rotation, drag, and losses due to a finite number of blades. - A simple 'optimum' blade design including wake rotation and an infinite number of blades. This blade design can be used as the start for a general blade design analysis.

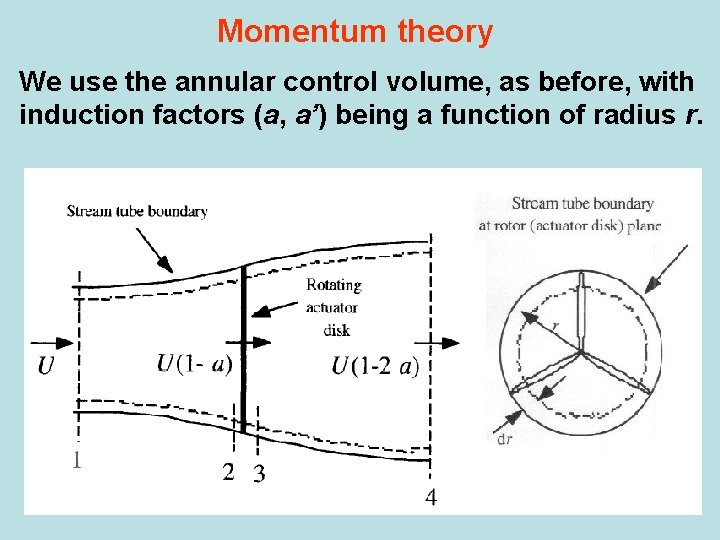
Momentum theory We use the annular control volume, as before, with induction factors (a, a’) being a function of radius r.

Applying linear momentum conservation to the CV of radius r and thickness dr gives the thrust contribution as: Similarly, from conservation of angular momentum, the differential torque, Q, imparted to the blades (and equally, but oppositely, to the air) is: Together, these define thrust and torque on an annular section of the rotor as functions of axial and angular induction factors that represent the flow conditions.

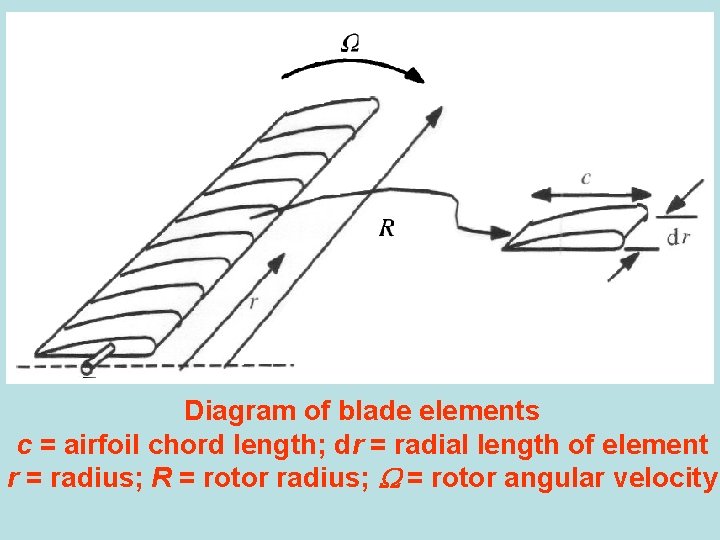
Blade element theory The forces on the blades of a wind turbine can also be expressed as a function of Cl, Cd and . For this analysis, the blade is assumed to be divided into N sections (or elements). Assumptions: - There is no aerodynamic interaction between elements. - The forces on the blades are determined solely by the lift and drag characteristics of the airfoil shape of the blades.

Diagram of blade elements c = airfoil chord length; dr = radial length of element r = radius; R = rotor radius; = rotor angular velocity

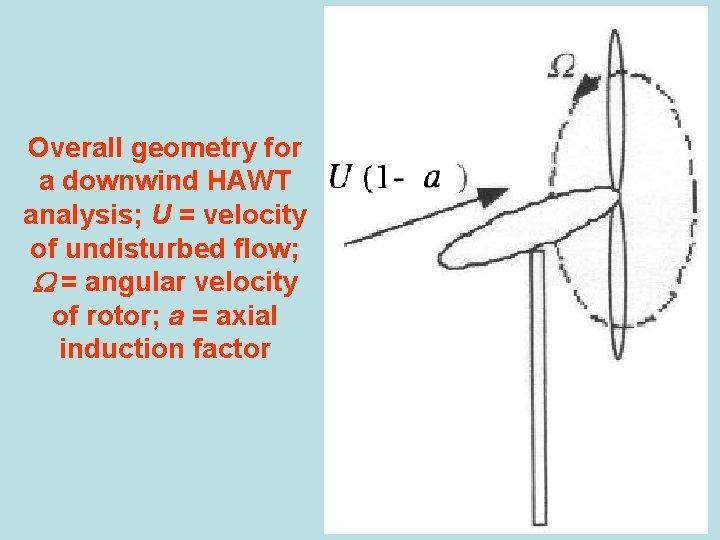
Note: Lift and drag forces are perpendicular and parallel, respectively, to an effective, or relative, wind. The relative wind is the vector sum of the wind velocity at the rotor, U (1 - a), and the wind velocity due to rotation of the blade. This rotational component is the vector sum of the blade section velocity, r, and the induced angular velocity at the blades from conservation of angular momentum, r / 2, or:

Overall geometry for a downwind HAWT analysis; U = velocity of undisturbed flow; = angular velocity of rotor; a = axial induction factor

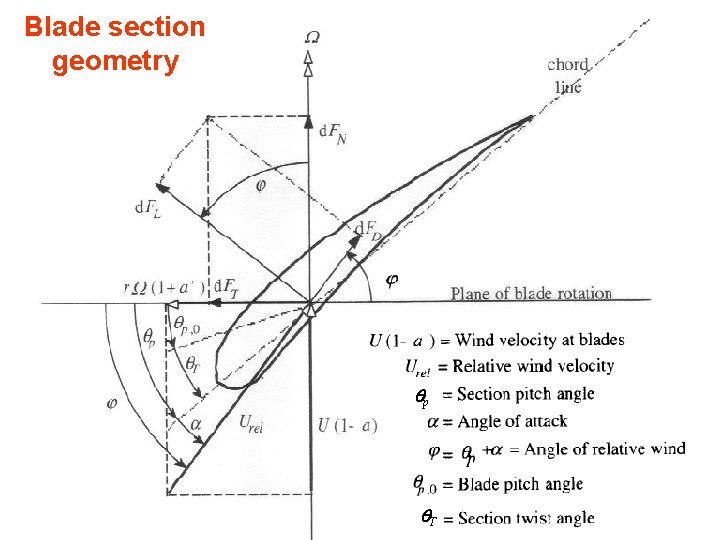
Blade section geometry p T

p = section pitch angle (angle between chord line and plane of rotation) p, 0 = blade pitch angle at tip T = blade twist angle = p - p, 0 = angle of attack (angle between chord line and relative wind) = angle of relative wind = p + d. FL = incremental lift force d. FD = incremental drag force d. FN = incremental force normal to plane of rotation (this contributes to thrust) d. FT = incremental force tangential to circle swept by rotor (creates useful torque) Ure. I = the relative wind velocity.

Figure shows the following section relationships: If rotor has B blades, total normal force on section at distance r from centre is:

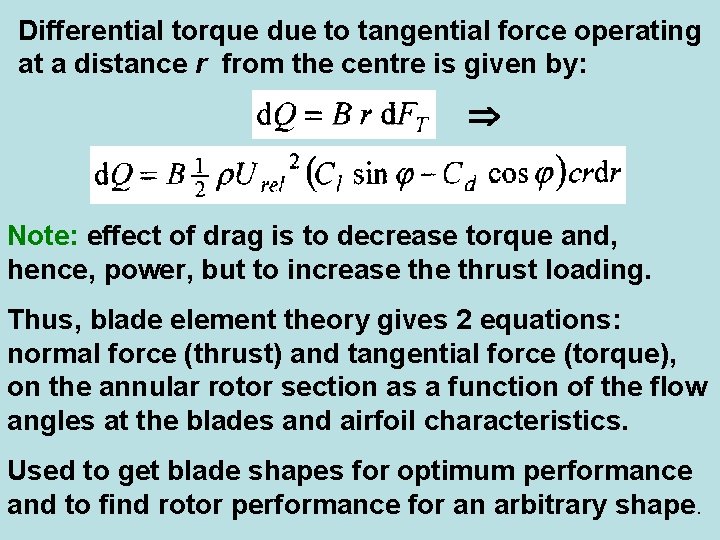
Differential torque due to tangential force operating at a distance r from the centre is given by: Note: effect of drag is to decrease torque and, hence, power, but to increase thrust loading. Thus, blade element theory gives 2 equations: normal force (thrust) and tangential force (torque), on the annular rotor section as a function of the flow angles at the blades and airfoil characteristics. Used to get blade shapes for optimum performance and to find rotor performance for an arbitrary shape.

Blade shape for ideal rotor (no wake rotation) Because the algebra can get complex, a simple, but useful example will be presented here to illustrate the method. Earlier, the maximum possible power coefficient from a wind turbine, assuming no wake rotation or drag, was found to occur with an axial induction factor of 1/3. If the same simplifying assumptions are applied to the momentum and blade element equations, the analysis becomes simple enough that an ideal blade shape can be determined (= approx. shape to give maximum power at the design tip speed ratio).

The following assumptions will be made: - No wake rotation; thus a' = 0 - No drag; thus Cd = 0 - No losses from a finite number of blades - For the Betz optimum rotor, a = 1/3 in each annular stream tube First, a design tip speed ratio, , the desired number of blades, B, the radius, R, and an airfoil with known lift and drag coefficients as a function of angle of attack need to be chosen. An angle of attack (and, thus, a lift coefficient at which the airfoil will operate) is also chosen.

This angle of attack should be selected where Cd / Cl is minimum in order to most closely approximate the assumption that Cd = 0. These choices allow the twist and chord distribution of a blade that would provide Betz limit power production (given the input assumptions) to be determined. For = 1/3 momentum theory gives the incremental thrust on an annular element as:

From blade element theory equation (with Cd = 0) the normal force on the element is: Urel can be expressed in terms of other variables: Combining results from the two theories (the above equations for d. T and d. FN) with that for Urel gives:

Using: with a’ = 0 and a = 1/3 gives: so that: Rearranging, using r = (r/R), the angle of the relative wind, , and the blade chord, c, at each section are:

These equations may be used to find the chord and twist distribution of the Betz optimum blade. Example: Given = 7, R = 5 m, Cl = 1, Cd/Cl is minimum at = 7, and there are 3 blades (B = 3) we can use: and together with and to obtain the changes in chord, twist angle (= 0 at tip), angle of relative wind, and section pitch, with radial distance, r/R, along the blade:

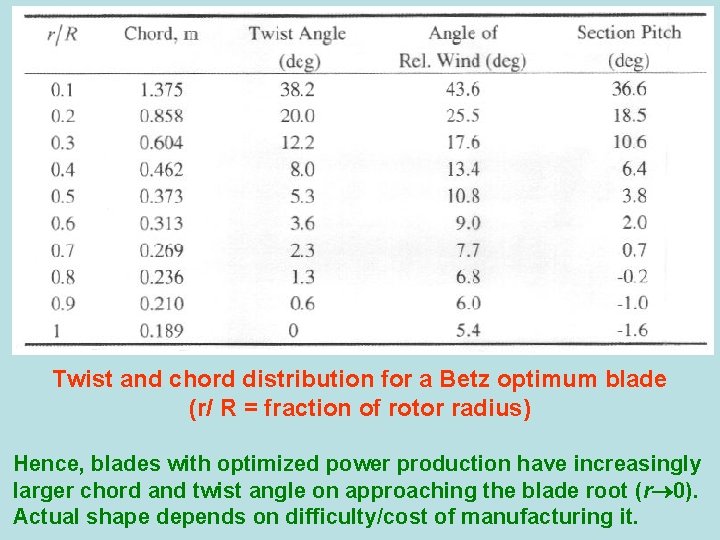
Twist and chord distribution for a Betz optimum blade (r/ R = fraction of rotor radius) Hence, blades with optimized power production have increasingly larger chord and twist angle on approaching the blade root (r 0). Actual shape depends on difficulty/cost of manufacturing it.

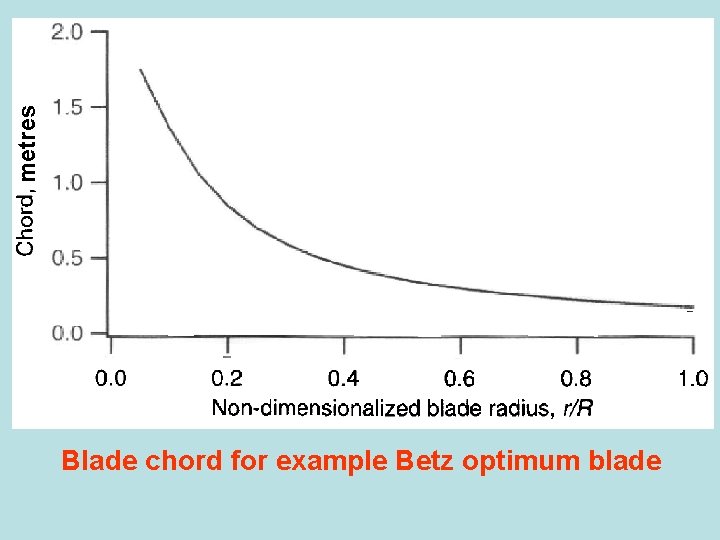
metres Blade chord for example Betz optimum blade

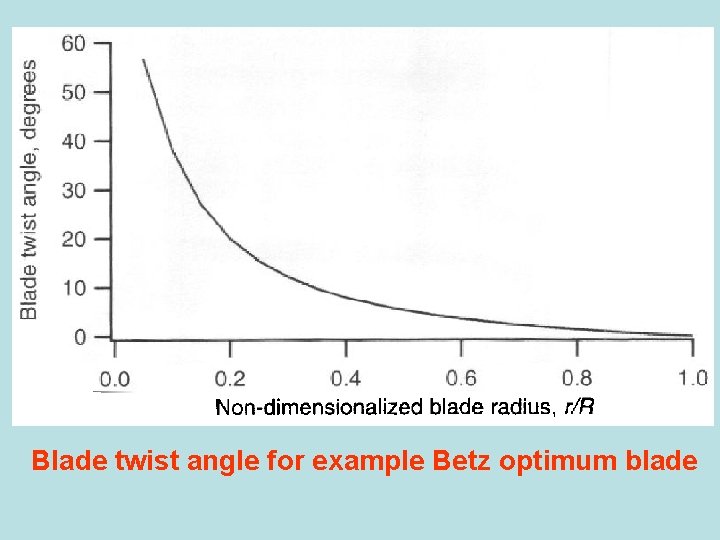
Blade twist angle for example Betz optimum blade

Prediction of general blade shape performance Generally, rotor shape is not optimum because of fabrication difficulties. Also when an 'optimum' blade is run at an offdesign tip speed ratio it is no longer 'optimum'. Thus, blade shape must be designed for - easy fabrication, and - overall performance over the range of wind and rotor speeds that they will encounter.

For non-optimum blades use an iterative method. We assume a blade shape, predict its performance, try another shape and repeat until a suitable blade has been chosen. So far, the blade shape for an ideal rotor without wake rotation has been considered. Now we’ll consider analysis of arbitrary blade shapes, including; wake rotation, drag, losses from a finite number of blades and off-design performance. This leads to determination of an optimum blade shape, including wake rotation as part of a complete rotor design procedure.

Strip theory for a generalized rotor, including wake rotation Here we extend our previous analysis to consider the non-linear range of the Cl v. curve (i. e. stall). The analysis starts with the 4 equations derived from momentum and blade element theories. In this analysis, it is assumed that the chord and twist distributions of the blade are known. is unknown, but additional equations can be used to solve for and the performance of the blade. The forces and moments derived from the 2 theories must be equal. Equating these, one can derive the flow conditions for a turbine design.

Momentum theory From axial momentum: From angular momentum: Blade element theory where thrust d. T is same force as normal force d. FN

Using the expression for the relative velocity: The blade element theory equations become: where ’ = local solidity defined by ’ = B c / 2 r

Blade element momentum theory When calculating induction factors, a and a', usual practice is to set Cd = 0. For airfoils with low Cd, this simplification gives negligible errors. When the torque equations and normal force equations are equated between momentum and blade element theory, with Cd = 0, we obtain: From torque: From force:

These 2 equations, together with: yield the useful relationships: others may also be derived, including: Now, we need to examine some solution methods.

Solution methods Two solution methods use these equations to determine the flow conditions and forces at each blade section. The first uses measured airfoil characteristics and BEM equations to solve directly for Cl and . Can be solved numerically, but also has a graphical solution that shows the flow conditions at the blade and the existence of multiple solutions. The second solution is an iterative numerical approach that is most easily extended for flow conditions with large axial induction factors.

Method 1 - Solving for Cl and . Since = + p for a given blade geometry and operating conditions, there are two unknowns in Cl and at each section. To find these, one can use the empirical Cl v. curves for the chosen airfoil, picking off the Cl and that satisfy the above equation. This can be done either numerically, or graphically (next slide). Once Cl and have been found, a' and a can be determined from any two of:

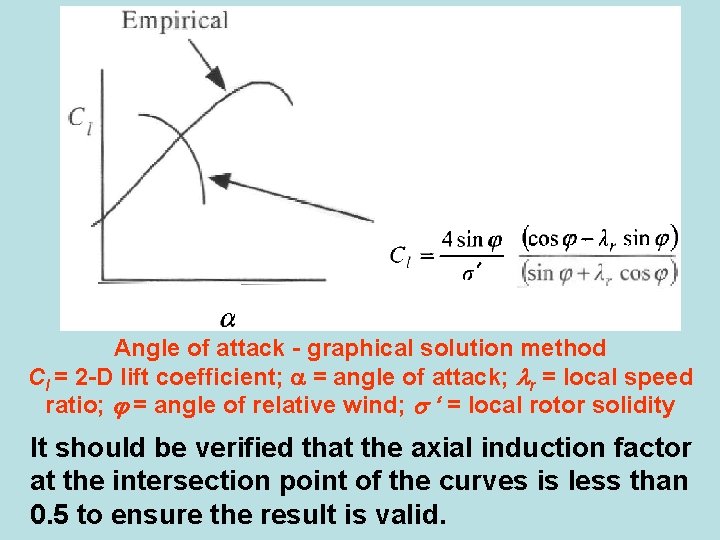
Angle of attack - graphical solution method Cl = 2 -D lift coefficient; = angle of attack; r = local speed ratio; = angle of relative wind; ‘ = local rotor solidity It should be verified that the axial induction factor at the intersection point of the curves is less than 0. 5 to ensure the result is valid.

Method 2 - Iterative solution for a and a'. Starts with guesses for a and a', from which flow conditions and new inductions factors are calculated: (1) Guess values of a and a' (2) Calculate the angle of the relative wind from (3) Calculate from = + p and then CI and Cd (4) Update a and a' from either: or The process is then repeated until the newly calculated induction factors are within some acceptable tolerance of the previous ones.

Calculation of power coefficient Once a has been obtained from each section, the overall rotor power coefficient may be calculated (see Appendix B): where h = local speed ratio at the hub. This may also be expressed as: Usually, these equations are solved numerically. When Cd = 0 the first equation here is the same as that derived from m’tum theory with wake rotation.

Tip loss: effect on power coefficient of number of blades Because pressure on the suction side of a blade is lower than on the pressure side, air tends to flow around the tip from the lower to upper surface, reducing lift and hence power production near the tip (most noticeable with fewer, wider blades). Simplest method for this is a correction factor, F, introduced into the previously discussed equations, which is a function of the number of blades, the angle of relative wind, and position on the blade: Note: 0 F 1

The tip loss correction factor affects the forces derived from momentum theory. Thus, we end up with: Other equations become:

The equation remains unchanged. The power coefficient can be calculated from: or

Off-design performance When a section of blade has a pitch angle or flow conditions that are very different from the design conditions, a number of complications can affect the analysis. These include: - Multiple solutions in the region of transition to stall, and - Solutions for highly loaded conditions with values of the axial induction factor approaching and exceeding 0. 5.

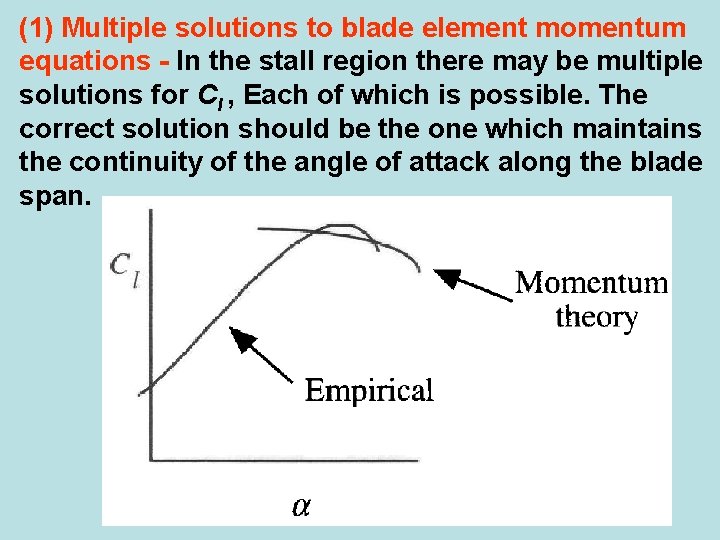
(1) Multiple solutions to blade element momentum equations - In the stall region there may be multiple solutions for CI , Each of which is possible. The correct solution should be the one which maintains the continuity of the angle of attack along the blade span.

(2) Wind turbine flow states – Measured turbine performance is close to the results of BEM theory at low values of the axial induction factor, a. M’tum theory is no longer valid at a > 0. 5, because the wind velocity in the far wake would be -ve. In fact, as a > 0. 5, flow patterns through the turbine become more complex than those predicted by momentum theory. A number of operating states for a rotor have been identified, notably: Windmill state - normal turbine operating state. Turbulent wake state - operation in high winds.

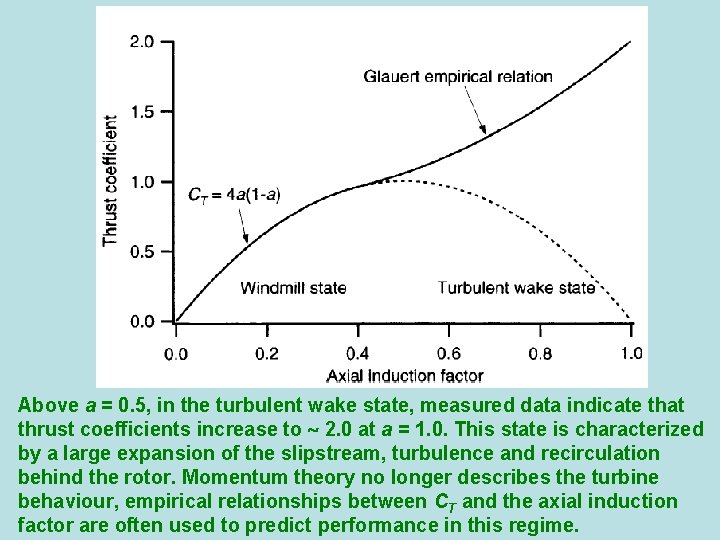
Above a = 0. 5, in the turbulent wake state, measured data indicate that thrust coefficients increase to 2. 0 at a = 1. 0. This state is characterized by a large expansion of the slipstream, turbulence and recirculation behind the rotor. Momentum theory no longer describes the turbine behaviour, empirical relationships between CT and the axial induction factor are often used to predict performance in this regime.

Turbulent wake state rotor modelling In the turbulent wake state thrust determined by momentum theory is no longer valid. In these cases, the previous analysis can lead to a lack of convergence to a solution or a situation in which the curve would lie below the airfoil lift curve. In the turbulent wake state, a solution can be found by using an empirical relationship between the axial induction factor and the thrust coefficient in conjunction with blade element theory. The empirical relationship by Glauert (shown in previous figure) including tip losses, is: Valid for a > 0. 4 or CT > 0. 96

The local thrust coefficient at a given annular section at radius, r, may be defined as: so using: the local thrust coefficient is:

The easiest solution approach for heavily loaded turbines is the iterative procedure (Method 2) that starts with the selection of possible values for a and a'. Once and Cl and Cd have been determined, the local thrust coefficient can be calculated according to the last equation. If CTr < 0. 96 then the previously derived equations can be used. If CTr > 0. 96 then the next estimate for a should use the local thrust coefficient with Then a' is given by

Blade shape for an optimum rotor with wake rotation May be found using the analysis developed for a general rotor. This optimisation includes wake rotation, but ignores drag (Cd = 0 ) and tip losses (F = 1). Optimization is done by taking the partial derivative of that part of the integral for Cp which is a function of the angle of the relative wind, , and setting it equal to zero:

This gives: whilst more algebra gives: Induction factors can be calculated from: These results can be compared to those for an ideal blade without wake rotation:

As before, we select where Cd / Cl is a minimum. Solidity is the ratio of the area of the blades to the swept area: When the blade is modelled as a set of N blade sections of equal span, the solidity can be calculated from:

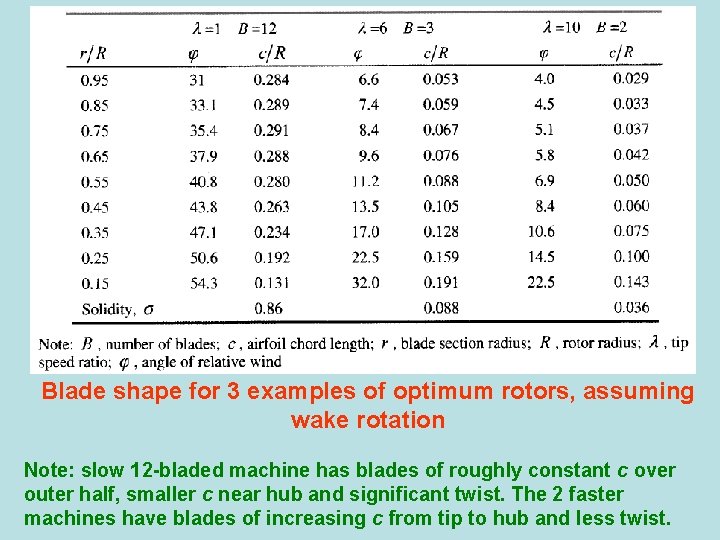
Blade shape for 3 examples of optimum rotors, assuming wake rotation Note: slow 12 -bladed machine has blades of roughly constant c over outer half, smaller c near hub and significant twist. The 2 faster machines have blades of increasing c from tip to hub and less twist.

Generalized rotor design procedure (1) Rotor design for specific conditions The previous analysis can be used in a generalized rotor design procedure: (a) Choose various rotor parameters and an airfoil. (b) An initial blade shape is then determined using the optimum blade shape assuming wake rotation (c) The final blade shape and performance are determined iteratively considering drag, tip losses, and ease of manufacture.

Determination of basic rotor parameters 1. Decide what power, P, is needed at a particular wind velocity, U. Include effect of a probable Cp and efficiencies, , of various other components (gearbox, generator, pump, etc). The radius, R, of the rotor may be estimated from: 2. According to application, choose a tip speed ratio, . For a water pumping windmill (greater torque needed) use 1 < < 3. For electric power generation, use 4 < < 10. Higher speed machines use less material in the blades and have smaller gearboxes, but require more sophisticated airfoils.

3. Choose a number of blades, B, from table below. Note: If fewer than three blades are selected, there a number of structural dynamic problems that must be considered in the hub design. Suggested blade number, B, for different tip speed ratios, 4. Select an airfoil. If < 3, curved plates can be used. For > 3 use a more aerodynamic shape.

Definition of the blade shape 5. Obtain and examine the empirical curves for the aerodynamic properties of the airfoil at each section (airfoil may vary from the root to the tip), i. e. Cl vs. , Cd vs. . Choose the design aerodynamic conditions, Cl, design and design , such that Cd, design / Cl, design is at a minimum for each blade section. 6. Divide the blade into N elements (usually 10 -20). Use the optimum rotor theory to estimate the shape of the i th blade with a midpoint radius of ri using:

7. Using the optimum blade shape as a guide, select a blade shape that looks like a good approximation. For ease of fabrication, linear variations of chord, thickness and twist might be chosen. For example, if a 1, b 1 and a 2 are coeffs. for the chosen chord and twist distributions, then the chord and twist can be expressed as:

Calculate rotor performance & modify blade design 8. As outlined above, one of two methods may be used to solve the blade performance equations. Method 1 - Solving for CI and : Find the actual and Cl for the centre of each element, using the following equations and the empirical airfoil curves:

Cl and can be found by iteration or graphically: Graphical solution for at section i The iterative approach needs an initial estimate of the tip loss factor. To find a starting Fi , use an estimate for the angle of the relative wind of: Subsequent iterations, find Fi using: where j is the number of the iteration. Finally, compute the axial induction factor: ai If ai > 0. 4 , use Method 2

Method 2 – Iteration to find a and a’: For an initial guess use values from the adjacent blade section, values from a previous design or an estimate based on values from the initial optimum blade design: ai, 1

Using guesses for ai, 1 and a’i, 1 start the iterative solution procedure for the jth iteration. For the first iteration j = 1. Calculate the angle of the relative wind and the tip loss factor: Determine Cl, i, j and Cd, i, j from airfoil lift and drag data using:

Calculate the local thrust coefficient: Update a and a’ for the next iteration. If CTr, I, j < 0. 96 : If CTr, I, j > 0. 96 : Until convergence use j = j+1 and iterate again starting from the eqn for tan i, j

9. Having solved the equations for the performance at each blade element, the power coefficient is determined using: If total length of hub and blade is assumed to be divided into N equal length blade elements, then: where k is the index of the first "blade" section consisting of the actual blade airfoil.

10. Modify design if necessary and repeat steps 8 - 10, in order to find the best design for the rotor, given the limitations of fabrication.

(2) Cp - curves Once the blade has been designed for optimum operation at a specific design tip speed ratio, rotor performance over all expected tip speed ratios needs to be determined. This can be done using methods outlined earlier. For each tip speed ratio, the aerodynamic conditions at each blade section need to be determined. From these, the performance of the total rotor can be determined. The results are usually presented as a graph of power coefficient versus tip speed ratio, called a Cp - curve:

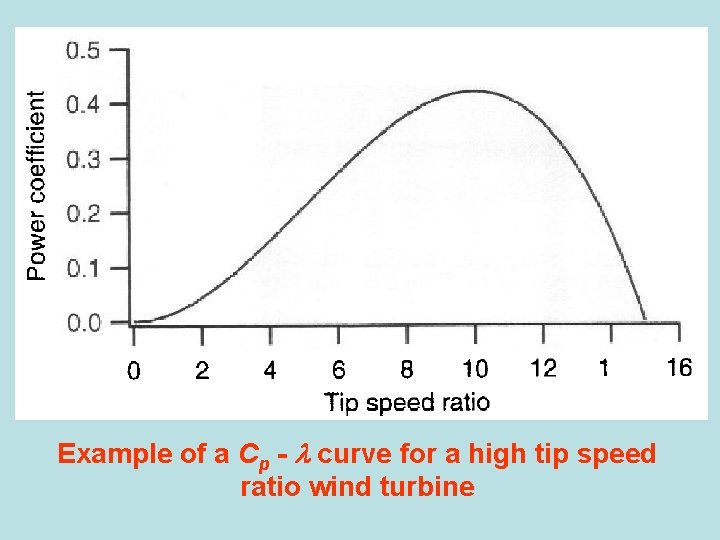
Example of a Cp - curve for a high tip speed ratio wind turbine

Cp - curves can be used in wind turbine design to determine the rotor power for any combination of wind and rotor speed. They provide immediate information on the maximum rotor power coefficient and optimum tip speed ratio. The data can be found from turbine tests or from modelling. In either case, the results depend on the lift and drag coefficients of the airfoils, which may vary as a function of the flow conditions (e. g. vary with Re).

Simplified HAWT performance Calculation procedure The method uses blade element theory and incorporates an analytical method for finding . Depending on whether tip losses are included, few or no iterations are required. The method assumes that 2 conditions apply: (1) The airfoil section Cl vs must be linear in the region of interest. (2) must be small enough that small-angle approximations may be used.

The simplified method is same as Method 1 before, with the exception of a simplification for determining and Cl for each blade section. The simplified method uses an analytical (closedform) expression for finding of the relative wind at each blade element. It is assumed that the lift and drag curves can be approximated by: (1) (2) When the lift curve is linear and when small-angle approximations can be used, it can be shown that is given by:

(3) where

can be calculated from (3) once an initial estimate for the tip loss factor (F) is determined. The lift and drag coefficients can then be calculated from Equation (1) and (2), using Iteration with a new estimate of the tip loss factor may be required.

Effect of drag and blade number on optimum performance Earlier the max. theoretically possible power coeff. for wind turbines was determined as a function of tip speed ratio. Later we saw that airfoil drag and tip losses (that are a function of the total number of blades) reduce the power coeffs. of wind turbines. The maximum achievable power coeff. for turbines with an optimum blade shape but a finite number of blades and aerodynamic drag has been calculated to within 0. 5% for tip speed ratios from 4 to 20, lift to drag ratios (Cl / Cd) from 25 to infinity and from 1 to 3 blades (B):

The following two plots show the variation of maximum achievable power coefficient with tip speed ratio, as a function of: (1) Number of blades (no drag) (2) Lift to drag ratio In practice these coefficients are reduced even further by the need to use non-optimum designs that are easy to manufacture, the lack of airfoils at the hub and aerodynamic losses at the blade-hub intersection.

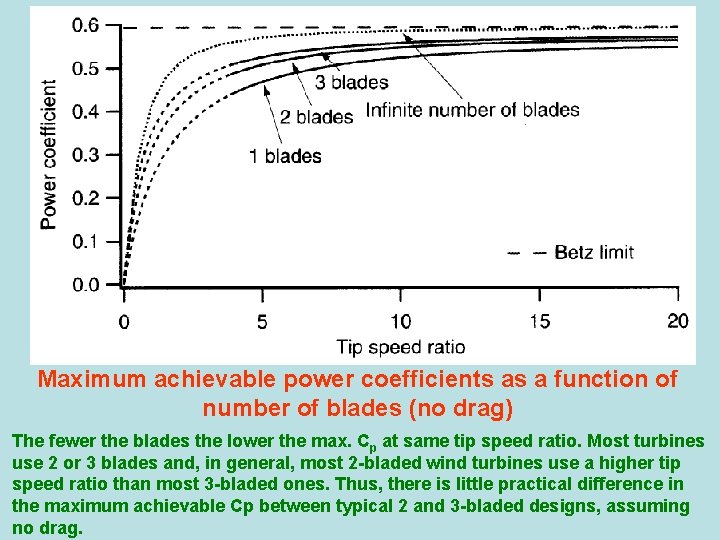
Maximum achievable power coefficients as a function of number of blades (no drag) The fewer the blades the lower the max. Cp at same tip speed ratio. Most turbines use 2 or 3 blades and, in general, most 2 -bladed wind turbines use a higher tip speed ratio than most 3 -bladed ones. Thus, there is little practical difference in the maximum achievable Cp between typical 2 and 3 -bladed designs, assuming no drag.

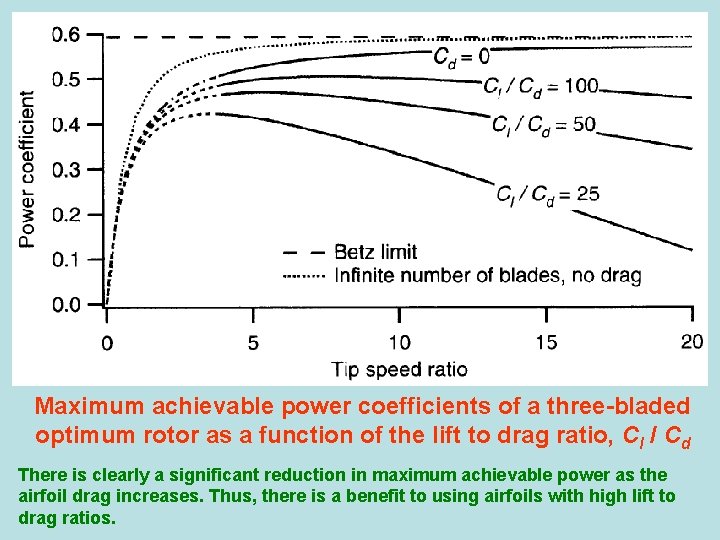
Maximum achievable power coefficients of a three-bladed optimum rotor as a function of the lift to drag ratio, CI / Cd There is clearly a significant reduction in maximum achievable power as the airfoil drag increases. Thus, there is a benefit to using airfoils with high lift to drag ratios.

Appendix A – Determining Weibull parameters (k and c) from mean and standard deviation wind speed values

Using the Weibull probability density distribution function p(U), it is possible to calculate the average velocity as follows: (Eqn. 1)

(Eqn 2) Equation (1) can then be used to solve for c : (2)


Variation of parameters with Weibull k shape factor It should be noted that a Weibull distribution for which k = 2 is a special case. It equals the Rayleigh distribution. That is, for k = 2 2 (1+ ½) = / 4. One can also note that U / U = 0. 523 for a Rayleigh distribution.

Appendix B – Derivation of power coefficient equation for blade analysis

The power contribution from each annulus is: where is the rotor rotational speed. The total power from the rotor is: where rh is the rotor radius at the hub of the blade. The power coefficient, Cp, is:

Using the expression for the differential torque: and the definition of the local tip speed ratio: where h = local speed ratio at the hub. From: we obtain:

Substituting: into we obtain the desired final equation:

Acknowledgement These notes are based on part of the book “Wind Energy Explained: Theory, Design and Application” by J F Manwell, J G Mc. Gowan and A L Rogers (published by Wiley). This is an excellent and comprehensive text, covering wind characteristics and resources, turbine aerodynamics, mechanics and dynamics (including structural design), electrical and control aspects, system integration, siting of turbines and economics.
 Eric savory
Eric savory Oxygen relative molecular mass
Oxygen relative molecular mass Lmtd heat exchanger formula
Lmtd heat exchanger formula Eric savory
Eric savory Eric savory
Eric savory What is the scientific notation for 832 000
What is the scientific notation for 832 000 Heather savory
Heather savory Savory parmo birmingham
Savory parmo birmingham Royal society of chemistry (rsc) publishing
Royal society of chemistry (rsc) publishing Energy conversion of a toaster
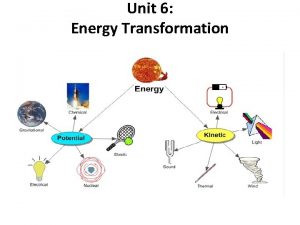
Energy conversion of a toaster Energy energy transfer and general energy analysis
Energy energy transfer and general energy analysis Energy energy transfer and general energy analysis
Energy energy transfer and general energy analysis Components of wind energy conversion system ppt
Components of wind energy conversion system ppt Electric kettle energy transformation
Electric kettle energy transformation What is radiant energy examples
What is radiant energy examples Fan energy transformation
Fan energy transformation Energy conversion and conservation
Energy conversion and conservation Energy transformation example
Energy transformation example Sound energy
Sound energy Energy conversion in transformer
Energy conversion in transformer Energy conversion table
Energy conversion table Energy meaning in science
Energy meaning in science Sound energy
Sound energy Windmill energy conversion
Windmill energy conversion Energy conversion examples
Energy conversion examples Investigation gagglekeierleber the
Investigation gagglekeierleber the What is the energy transformation of a car
What is the energy transformation of a car Transformer energy conversion
Transformer energy conversion Chemical potential energy images
Chemical potential energy images Potential energy of a spring at equilibrium
Potential energy of a spring at equilibrium Primary energy and secondary energy
Primary energy and secondary energy Primary energy and secondary energy
Primary energy and secondary energy Gibbs free energy spontaneous
Gibbs free energy spontaneous Negative free energy change
Negative free energy change W=fd
W=fd How are thermal energy and temperature different
How are thermal energy and temperature different A hairdryer converts ____ energy into ____ energy.
A hairdryer converts ____ energy into ____ energy. Gravitational potential energy definition
Gravitational potential energy definition How to convert mechanical energy to electrical energy
How to convert mechanical energy to electrical energy Section 3 using thermal energy worksheet answer key
Section 3 using thermal energy worksheet answer key Standard free energy change
Standard free energy change Helmholtz free energy
Helmholtz free energy As nutritional energy passes through the food chain it is
As nutritional energy passes through the food chain it is Usable chemical energy in food begins as __________ energy.
Usable chemical energy in food begins as __________ energy. Chapter 7 energy conservation of energy
Chapter 7 energy conservation of energy Wind energy is an indirect form of
Wind energy is an indirect form of ________ converts light energy into chemical energy. *
________ converts light energy into chemical energy. * Mechanical energy pics
Mechanical energy pics Elastic potential energy
Elastic potential energy Formula for electric field
Formula for electric field What is energy in physic
What is energy in physic Example of mechanical energy
Example of mechanical energy Gravitational potential energy vs kinetic energy
Gravitational potential energy vs kinetic energy Efficiency = useful power output
Efficiency = useful power output Mass and thermal energy
Mass and thermal energy Renewable energy and energy efficiency partnership
Renewable energy and energy efficiency partnership Potential vs kinetic energy
Potential vs kinetic energy Kinetic energy example
Kinetic energy example Potential energy of a spring at equilibrium
Potential energy of a spring at equilibrium Potential energy
Potential energy The change in mechanical energy
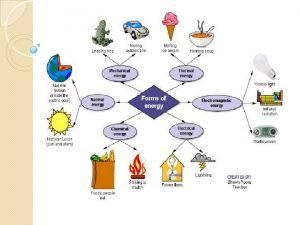
The change in mechanical energy Energy forms and energy conversions
Energy forms and energy conversions What is electromagnet
What is electromagnet In an energy pyramid where is the most energy
In an energy pyramid where is the most energy Photosynthesis transforms light energy into chemical energy
Photosynthesis transforms light energy into chemical energy Chapter 8 section 1: how organisms obtain energy
Chapter 8 section 1: how organisms obtain energy Eric kok delta lloyd
Eric kok delta lloyd Bioluminescence
Bioluminescence Eric van der geer
Eric van der geer Eric wernli
Eric wernli Wave by eric walters
Wave by eric walters Peperkamp ede
Peperkamp ede Ernest pharma
Ernest pharma Eric bihler
Eric bihler Eric laenen
Eric laenen Unclassified balance sheet
Unclassified balance sheet Eric s. roberts
Eric s. roberts Dr eric henley
Dr eric henley Eric andrew young
Eric andrew young éric está deprimido. cierto falso
éric está deprimido. cierto falso Jason eric johnson
Jason eric johnson Eric rotenberg
Eric rotenberg Banka nalog ric
Banka nalog ric Eric skunberg
Eric skunberg Eric leonidas
Eric leonidas Eric liddell quotes
Eric liddell quotes Eric chitambar
Eric chitambar Eric xing
Eric xing Eric xing
Eric xing Eric xing
Eric xing Eric clapton let it grow
Eric clapton let it grow Eric laithwaite gyroscope
Eric laithwaite gyroscope Asciisvg
Asciisvg Karthik sundaramoorthy
Karthik sundaramoorthy Eric grimson
Eric grimson Do not confuse theme with a story's
Do not confuse theme with a story's Eric meier model
Eric meier model Eric von ronheim
Eric von ronheim Eric arthur blair biography
Eric arthur blair biography Eric arthur
Eric arthur Food product design
Food product design Spy hansen
Spy hansen Music 1010
Music 1010 Where was eric clapton born
Where was eric clapton born Monique marcourt
Monique marcourt Grand nord automobile nieppe
Grand nord automobile nieppe 410ss
410ss Eric prebys uc davis
Eric prebys uc davis Eric rotenberg
Eric rotenberg Eric cant
Eric cant Eric carstensen
Eric carstensen Eric temmink
Eric temmink Eric raicovich
Eric raicovich Eric alu
Eric alu Eric blair author
Eric blair author Transaksi komplementer adalah
Transaksi komplementer adalah Eric prebys
Eric prebys Eric kee
Eric kee A hanging george orwell message
A hanging george orwell message Eric arthur blair
Eric arthur blair Eric allenbaugh
Eric allenbaugh Substantives direktfärben
Substantives direktfärben 1984 social classes
1984 social classes Ngjfg
Ngjfg Van berkum lochem
Van berkum lochem Eric d richards
Eric d richards Eric chien symantec
Eric chien symantec Eric hodgson
Eric hodgson Eric kallenborn
Eric kallenborn Eric abrial
Eric abrial Eric pitcher
Eric pitcher Eric daugas
Eric daugas Eric bueno
Eric bueno Eric onofre
Eric onofre Wr-2100 waveguide
Wr-2100 waveguide Eric oksenhendler
Eric oksenhendler Exemple protocole pluriprofessionnel
Exemple protocole pluriprofessionnel Eric wernli
Eric wernli Eric cawley
Eric cawley Eric von bismarck
Eric von bismarck Eric laureys
Eric laureys Nfpa 1700
Nfpa 1700 Eric p. xing
Eric p. xing Eric girardeau
Eric girardeau Lotf chapter 11
Lotf chapter 11 Upbpf
Upbpf Eric wauters
Eric wauters Graalvm python
Graalvm python Eric arthur blair
Eric arthur blair Why did eric blair change his name
Why did eric blair change his name Geometry extra credit
Geometry extra credit Eric berntsen
Eric berntsen Eric rosenberg md
Eric rosenberg md Eric mounier numération
Eric mounier numération Eric lazar
Eric lazar Eric wenger okc
Eric wenger okc Eric church biography
Eric church biography Dr eric berg plantar fasciitis
Dr eric berg plantar fasciitis Eric wengert
Eric wengert Transforaminal pronunciation
Transforaminal pronunciation