Chapter 8 Energy Energy Transfer And General Energy
















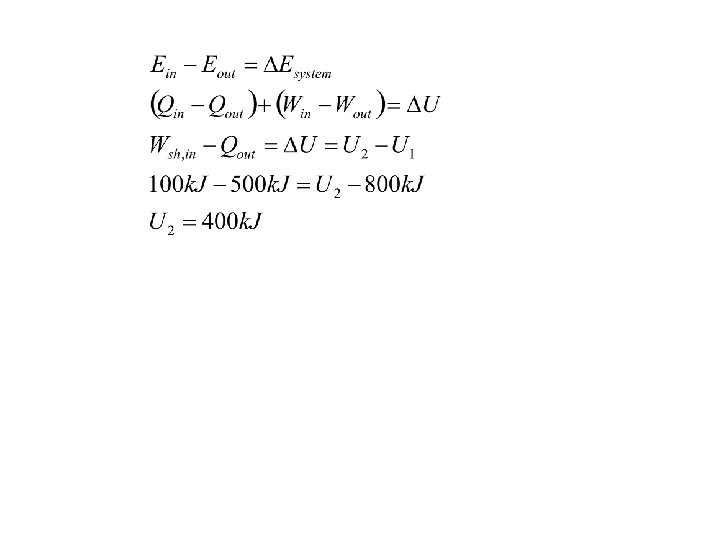


- Slides: 41

Chapter 8 Energy, Energy Transfer, And General Energy Analysis 1

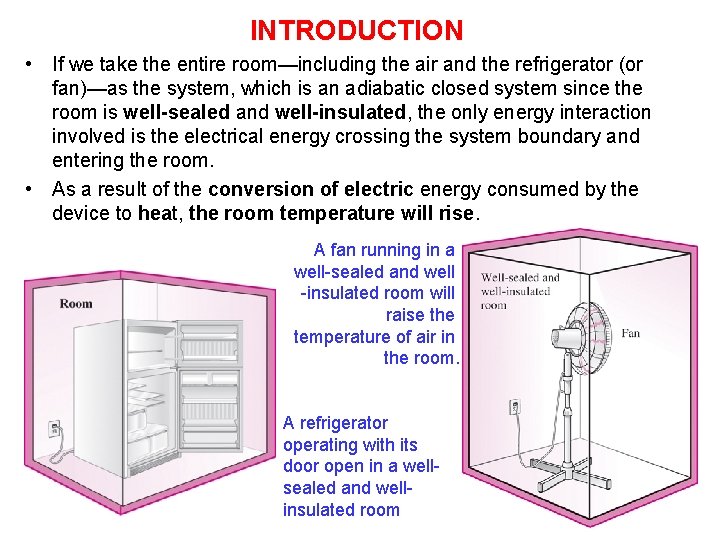
INTRODUCTION • If we take the entire room—including the air and the refrigerator (or fan)—as the system, which is an adiabatic closed system since the room is well-sealed and well-insulated, the only energy interaction involved is the electrical energy crossing the system boundary and entering the room. • As a result of the conversion of electric energy consumed by the device to heat, the room temperature will rise. A fan running in a well-sealed and well -insulated room will raise the temperature of air in the room. A refrigerator operating with its door open in a wellsealed and wellinsulated room

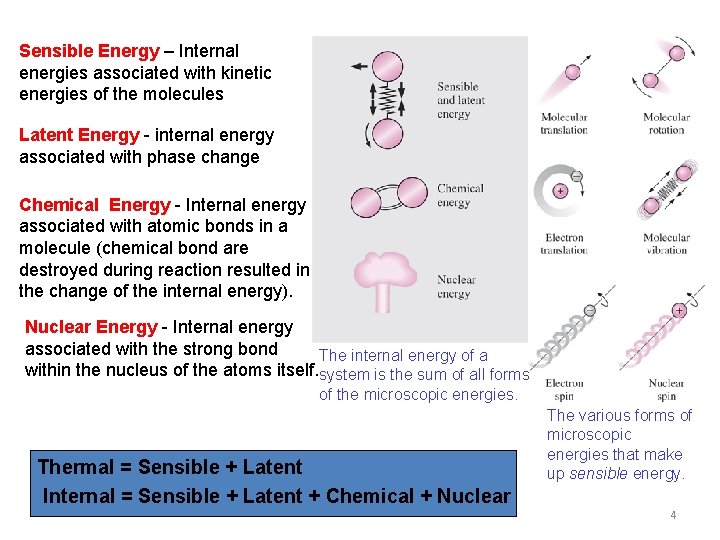
FORMS OF ENERGY • Energy can exist in numerous forms such as thermal, mechanical, kinetic, potential, electric, magnetic, chemical, and nuclear, and their sum constitutes the total energy, E (k. J) of a system. • Thermodynamics deals only with the change of the total energy. • Two groups of energy: macroscopic and microscopic. • Macroscopic forms of energy: Those a system possesses as a whole with respect to some outside reference frame (forms you can see), such as kinetic and potential energies. It is related to motion and the influence of some external effects such as gravity, electricity and surface tension. • Microscopic forms of energy: Those related to the molecular structure of a system and the degree of the molecular activity (forms that are hidden). • Internal energy, U(k. J): The sum of all the microscopic forms of energy (sensible, latent, chemical and nuclear).

Sensible Energy – Internal energies associated with kinetic energies of the molecules Latent Energy - internal energy associated with phase change Chemical Energy - Internal energy associated with atomic bonds in a molecule (chemical bond are destroyed during reaction resulted in the change of the internal energy). Nuclear Energy - Internal energy associated with the strong bond The internal energy of a within the nucleus of the atoms itself. system is the sum of all forms of the microscopic energies. Thermal = Sensible + Latent Internal = Sensible + Latent + Chemical + Nuclear The various forms of microscopic energies that make up sensible energy. 4

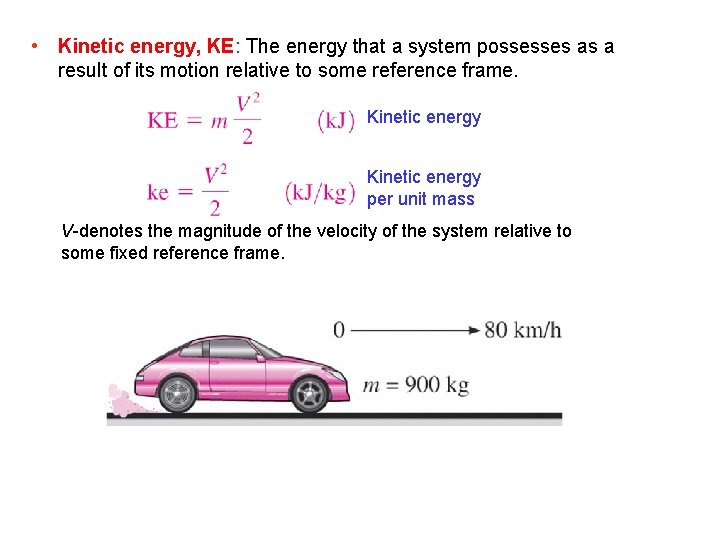
• Kinetic energy, KE: The energy that a system possesses as a result of its motion relative to some reference frame. Kinetic energy per unit mass V-denotes the magnitude of the velocity of the system relative to some fixed reference frame.

EXAMPLE Determine the specific kinetic energy of a mass whose velocity is 30 m/s, in k. J/kg • Potential energy, PE: The energy that a system possesses as a result of its elevation in a gravitational field. Potential energy per unit mass

EXAMPLE Determine the specific potential energy, in k. J/kg, of an object 50 m above a datum in a location where g = 9. 8 m/s 2 Total energy of a system consists of the kinetic, potential, and internal energies. Total energy of a system Energy of a system per unit mass

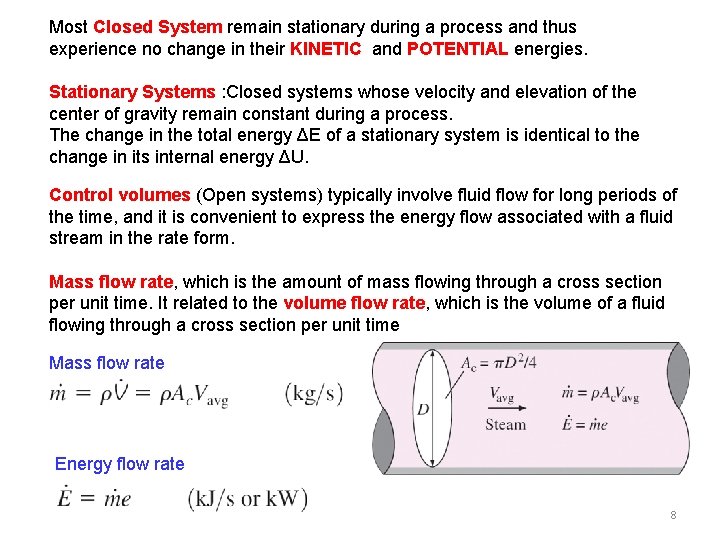
Most Closed System remain stationary during a process and thus experience no change in their KINETIC and POTENTIAL energies. Stationary Systems : Closed systems whose velocity and elevation of the center of gravity remain constant during a process. The change in the total energy ΔE of a stationary system is identical to the change in its internal energy ΔU. Control volumes (Open systems) typically involve fluid flow for long periods of the time, and it is convenient to express the energy flow associated with a fluid stream in the rate form. Mass flow rate, which is the amount of mass flowing through a cross section per unit time. It related to the volume flow rate, which is the volume of a fluid flowing through a cross section per unit time Mass flow rate Energy flow rate 8

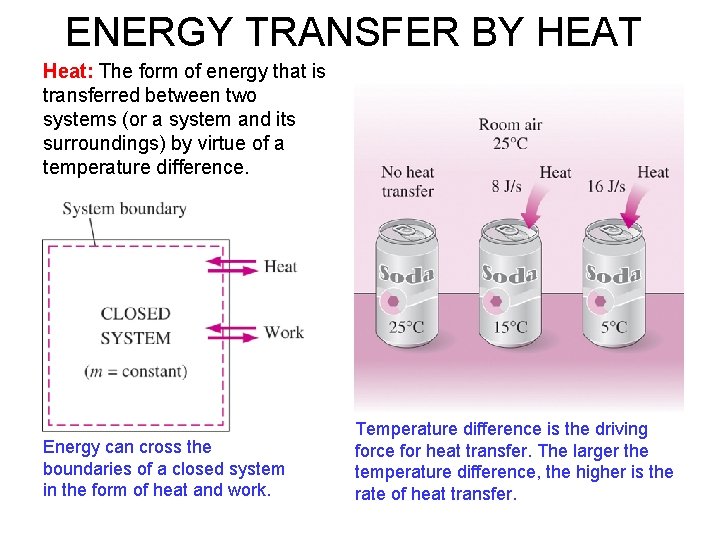
ENERGY TRANSFER BY HEAT Heat: The form of energy that is transferred between two systems (or a system and its surroundings) by virtue of a temperature difference. Energy can cross the boundaries of a closed system in the form of heat and work. Temperature difference is the driving force for heat transfer. The larger the temperature difference, the higher is the rate of heat transfer.

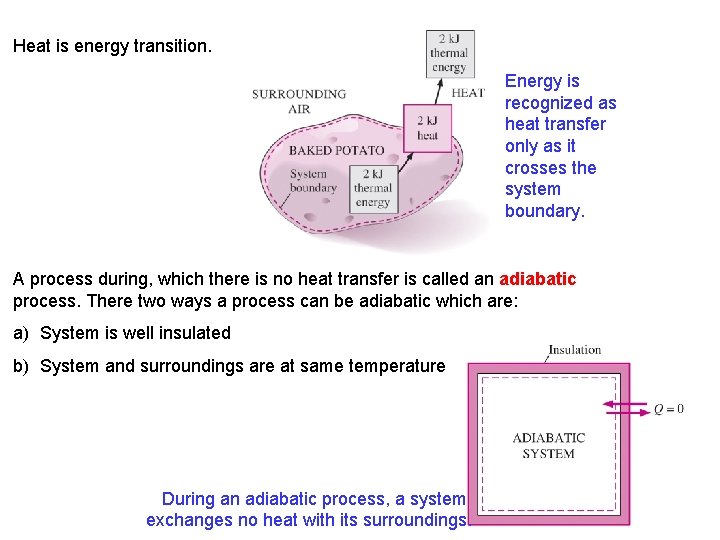
Heat is energy transition. Energy is recognized as heat transfer only as it crosses the system boundary. A process during, which there is no heat transfer is called an adiabatic process. There two ways a process can be adiabatic which are: a) System is well insulated b) System and surroundings are at same temperature During an adiabatic process, a system exchanges no heat with its surroundings. 10

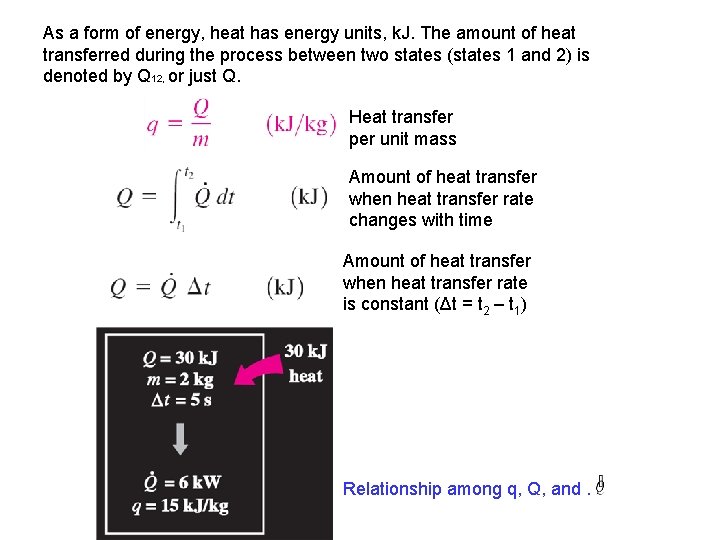
As a form of energy, heat has energy units, k. J. The amount of heat transferred during the process between two states (states 1 and 2) is denoted by Q 12, or just Q. Heat transfer per unit mass Amount of heat transfer when heat transfer rate changes with time Amount of heat transfer when heat transfer rate is constant (Δt = t 2 – t 1) Relationship among q, Q, and.

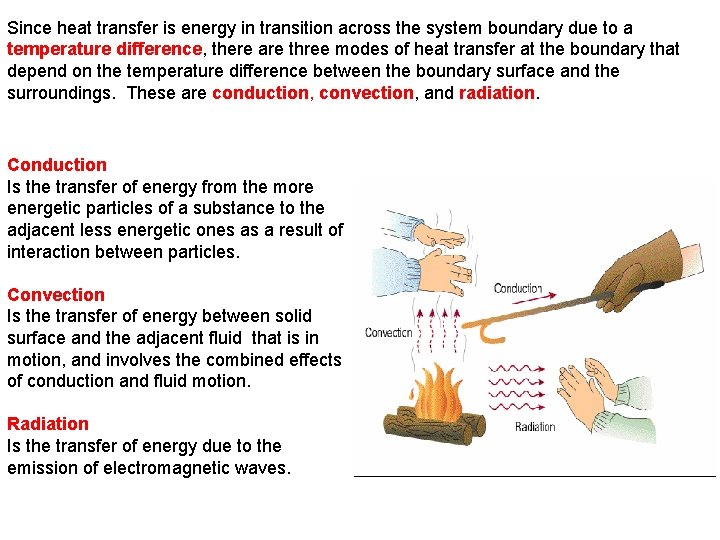
Since heat transfer is energy in transition across the system boundary due to a temperature difference, there are three modes of heat transfer at the boundary that depend on the temperature difference between the boundary surface and the surroundings. These are conduction, convection, and radiation. Conduction Is the transfer of energy from the more energetic particles of a substance to the adjacent less energetic ones as a result of interaction between particles. Convection Is the transfer of energy between solid surface and the adjacent fluid that is in motion, and involves the combined effects of conduction and fluid motion. Radiation Is the transfer of energy due to the emission of electromagnetic waves.

ENERGY TRANSFER BY WORK • If energy crosses boundary is not heat (due to temperature difference) then it is work [k. J or Btu] • More specifically, work is the energy transfer associated with a force acting through a distance • Units are – N. m or J; usually k. J in SI and • Examples include a rising piston, rotating shaft, current carrying wire, etc. • Rate of doing is work is called power with units of k. J/s or k. W

Energy Transport by Heat and Work and the Classical Sign Convention Energy may cross the boundary of a closed system only by heat or work. Energy transfer across a system boundary due solely to the temperature difference between a system and its surroundings is called heat. Energy transferred across a system boundary that can be thought of as the energy expended to lift a weight is called work. Heat and work are energy transport mechanisms between a system and its surroundings. The similarities between heat and work are as follows: 1. Both are recognized at the boundaries of a system as they cross the boundaries. They are both boundary phenomena. 2. Systems possess energy, but no heat or work. 3. Both are associated with a process, not a state. Unlike properties, heat or work has no meaning at a state. 4. Both are path functions (i. e. , their magnitudes depends on the path followed during a process as well as the end states. )

Since heat and work are path dependent functions, they have inexact differentials designated by the symbol . The differentials of heat and work are expressed as Q and W. The integral of the differentials of heat and work over the process path gives the amount of heat or work transfer that occurred at the system boundary during a process. That is, the total heat transfer or work is obtained by following the process path and adding the differential amounts of heat ( Q) or work ( W) along the way. The integrals of Q and W are not Q 2 – Q 1 and W 2 – W 1, respectively, which are meaningless since both heat and work are not properties and systems do not possess heat or work at a state.

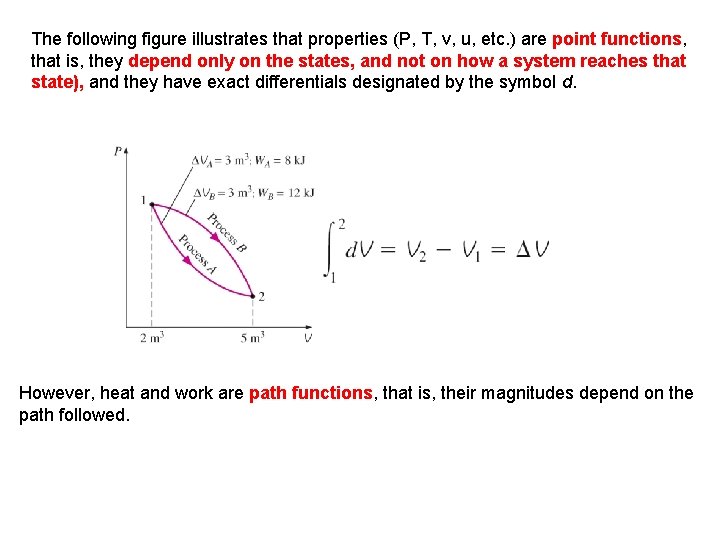
The following figure illustrates that properties T, v, u, etc. ) are point functions, Properties are(P, point functions that is, they depend only on the states, and not on how have exact differentials (d ). a system reaches that state), and they have exact differentials designated by the symbol d. However, heat and work are path functions, that is, their magnitudes depend on the path followed.

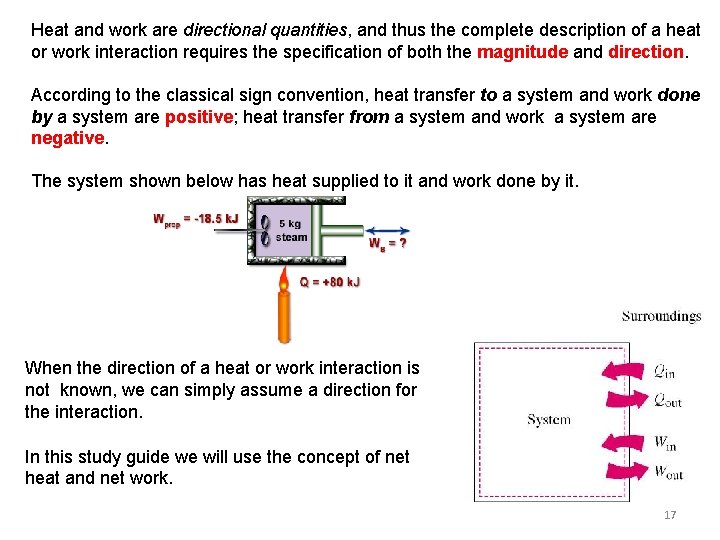
Heat and work are directional quantities, and thus the complete description of a heat or work interaction requires the specification of both the magnitude and direction. According to the classical sign convention, heat transfer to a system and work done by a system are positive; heat transfer from a system and work a system are negative. The system shown below has heat supplied to it and work done by it. When the direction of a heat or work interaction is not known, we can simply assume a direction for the interaction. In this study guide we will use the concept of net heat and net work. 17

EXAMPLE Traveling at a constant speed along a road. Determine the direction of the heat and work interactions, taking the following as the system: (a) the car radiator, (b) the car engine, (c) the car wheels, (d) the road, and (e) the air surrounding the car. (a) The car's radiator transfers heat from the hot engine cooling fluid to the cooler air. No work interaction occurs in the radiator. (b) The hot engine transfers heat to cooling fluid and ambient air while delivering work to the transmission. (c) The warm tires transfer heat to the cooler air and to some degree to the cooler road while no work is produced. No work is produced since there is no motion of the forces acting at the interface between the tire and road. (d) There is minor amount of heat transfer between the tires and road. Presuming that the tires are hotter than the road, the heat transfer is from the tires to the road. There is no work exchange associated with the road since it cannot move. (e) Heat is being added to the atmospheric air by the hotter components of the car. Work is being done on the air as it passes over and through the car.

EXAMPLE A personal computer is to be examined from a thermodynamic perspective. Determine the direction of the work and heat transfer (in and out) when the (a) keyboard, (b) monitor, (c) processing unit, and (d) all of are taken as the system. (a) As one types on the keyboard, electrical signals are produced and transmitted to the processing unit. Simultaneously, the temperature of the electrical parts is increased slightly. The work done on the keys when they are depressed is work done on the system (i. e. , keyboard). The flow of electrical current (with its voltage drop) does work on the keyboard. Since the temperature of the electrical parts of the keyboard is somewhat higher than that of the surrounding air, there is a transfer of heat from the keyboard to the surrounding air. (b) The monitor is powered by the electrical current supplied to it. This current (and voltage drop) is work done on the system (i. e. , monitor). The temperatures of the electrical parts of the monitor are higher than that of the surrounding air. Hence there is a heat transfer to the surroundings. (c) The processing unit is like the monitor in that electrical work is done on it while it transfers heat to the surroundings. (d) The entire unit then has electrical work done on it, and mechanical work done on it to depress the keys. It also transfers heat from all its electrical parts to the surroundings.

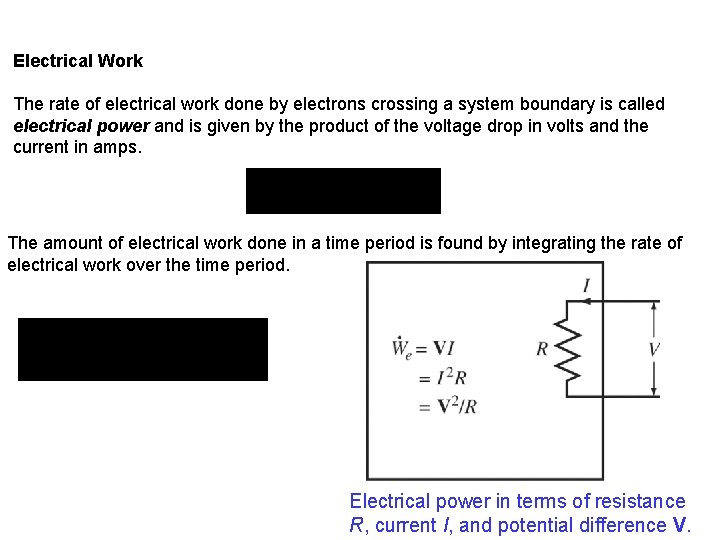
Electrical Work The rate of electrical work done by electrons crossing a system boundary is called electrical power and is given by the product of the voltage drop in volts and the current in amps. The amount of electrical work done in a time period is found by integrating the rate of electrical work over the time period. Electrical power in terms of resistance R, current I, and potential difference V.

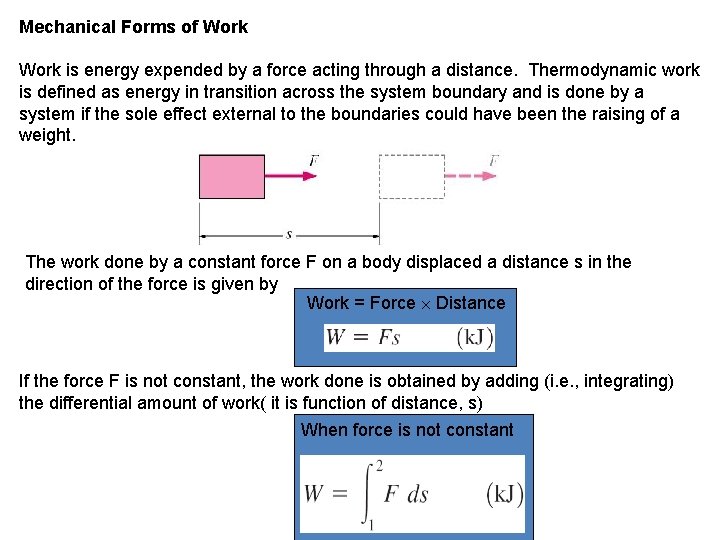
Mechanical Forms of Work is energy expended by a force acting through a distance. Thermodynamic work is defined as energy in transition across the system boundary and is done by a system if the sole effect external to the boundaries could have been the raising of a weight. The work done by a constant force F on a body displaced a distance s in the direction of the force is given by Work = Force Distance If the force F is not constant, the work done is obtained by adding (i. e. , integrating) the differential amount of work( it is function of distance, s) When force is not constant

There are two requirements for a work interaction between a system and its surrounding to exist: • There must be a force acting on the boundary • The boundary must move Common Types of Mechanical Work Energy • Shaft Work • Spring Work • Work done of Elastic Solid Bars • Work Associated with the Stretching of a Liquid Film • Work Done to Raise or to Accelerate a Body

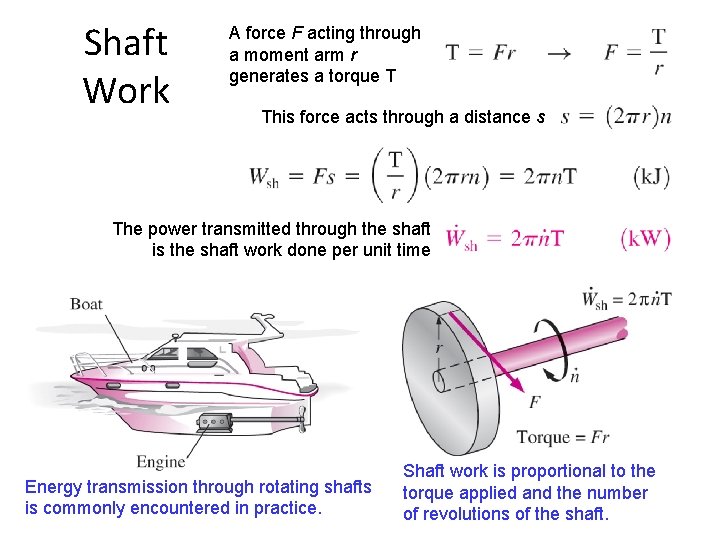
Shaft Work A force F acting through a moment arm r generates a torque T This force acts through a distance s Shaft work The power transmitted through the shaft is the shaft work done per unit time Energy transmission through rotating shafts is commonly encountered in practice. Shaft work is proportional to the torque applied and the number of revolutions of the shaft.

EXAMPLE Determine the power transmitted through the shaft of a car when the torque applied is 200 N. m and the shaft rotates at a rate of 4000 revolutions per minute (rpm) Solution

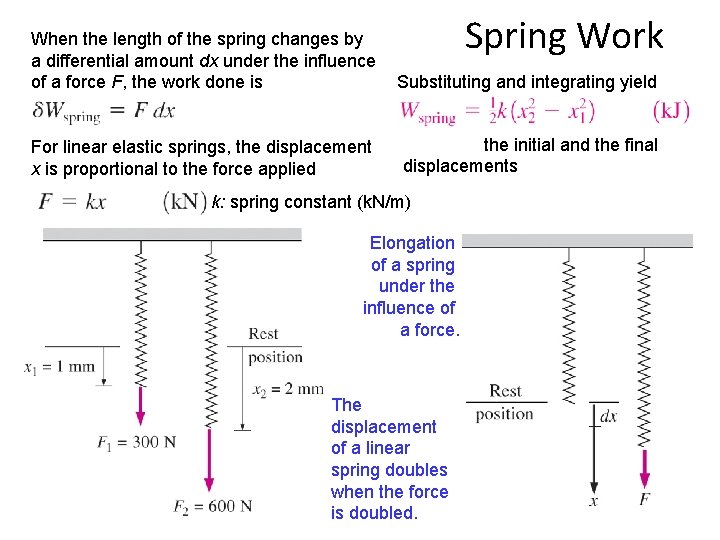
Spring Work When the length of the spring changes by a differential amount dx under the influence of a force F, the work done is Substituting and integrating yield For linear elastic springs, the displacement x is proportional to the force applied x 1 and x 2: the initial and the final displacements k: spring constant (k. N/m) Elongation of a spring under the influence of a force. The displacement of a linear spring doubles when the force is doubled.

EXAMPLE How much work, in k. J, can a spring whose spring constant is 3 k. N/cm produce after it has been compresses 3 cm from its unloaded length? Solution F x

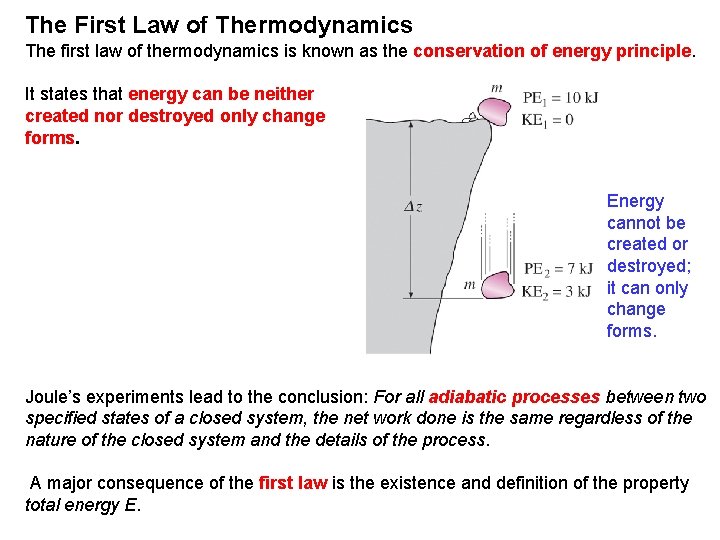
The First Law of Thermodynamics The first law of thermodynamics is known as the conservation of energy principle. It states that energy can be neither created nor destroyed; only change forms. Energy cannot be created or destroyed; it can only change forms. Joule’s experiments lead to the conclusion: For all adiabatic processes between two specified states of a closed system, the net work done is the same regardless of the nature of the closed system and the details of the process. A major consequence of the first law is the existence and definition of the property total energy E.

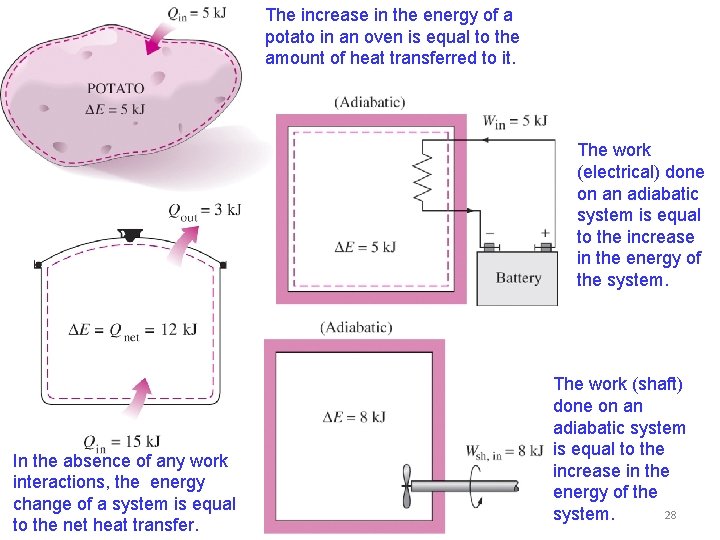
The increase in the energy of a potato in an oven is equal to the amount of heat transferred to it. The work (electrical) done on an adiabatic system is equal to the increase in the energy of the system. In the absence of any work interactions, the energy change of a system is equal to the net heat transfer. The work (shaft) done on an adiabatic system is equal to the increase in the energy of the 28 system.

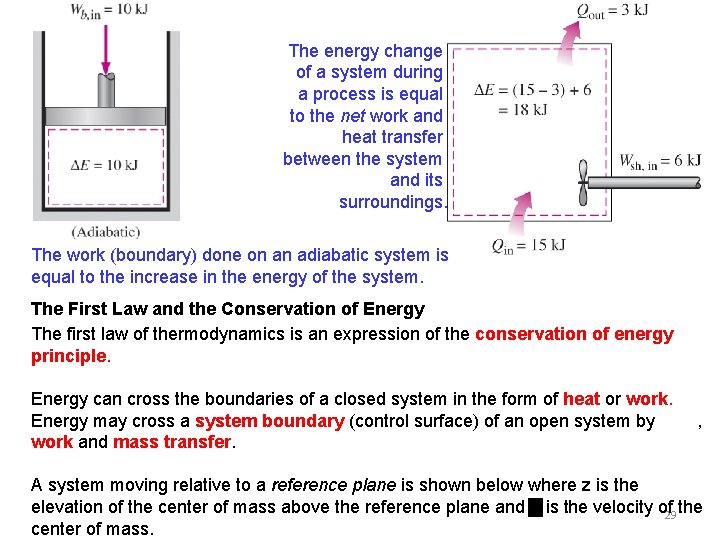
The energy change of a system during a process is equal to the net work and heat transfer between the system and its surroundings. The work (boundary) done on an adiabatic system is equal to the increase in the energy of the system. The First Law and the Conservation of Energy The first law of thermodynamics is an expression of the conservation of energy principle. Energy can cross the boundaries of a closed system in the form of heat or work. Energy may cross a system boundary (control surface) of an open system by heat, work and mass transfer. A system moving relative to a reference plane is shown below where z is the elevation of the center of mass above the reference plane and is the velocity of 29 the center of mass.

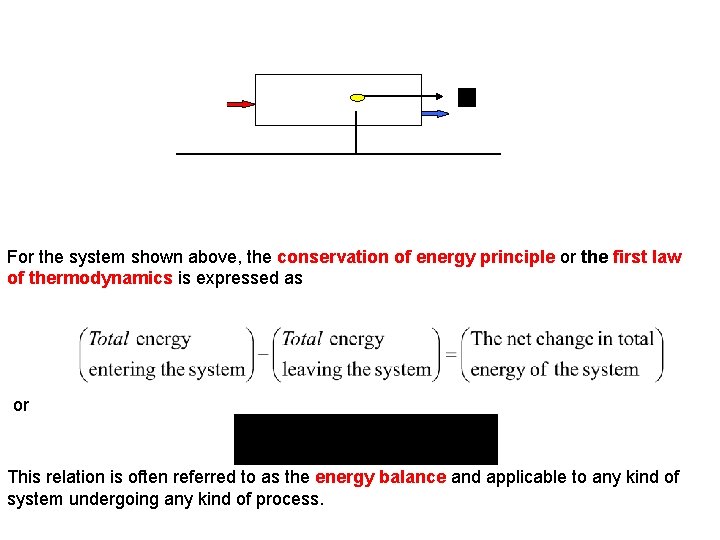
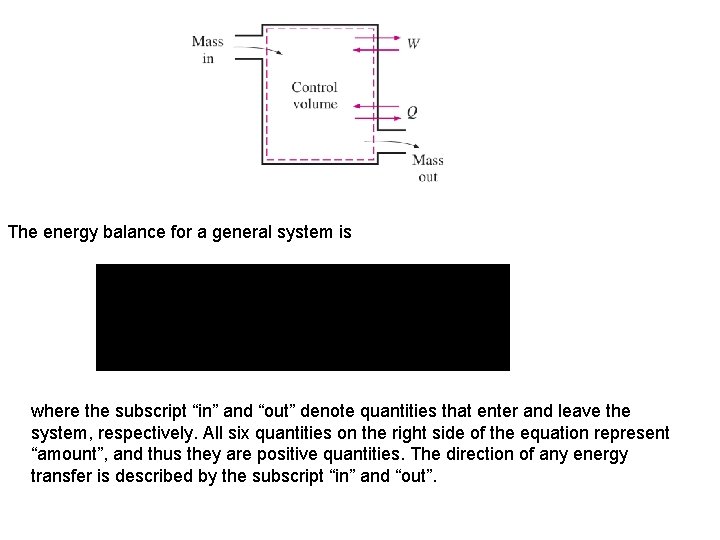
Energyin System CM z Energyout Reference Plane, z = 0 For the system shown above, the conservation of energy principle or the first law of thermodynamics is expressed as or This relation is often referred to as the energy balance and applicable to any kind of system undergoing any kind of process.

Energy Change of a System, ΔEsystem Determination of the energy of a system during a process involves the evaluation of the energy of the system at the beginning and at the end of the process, and taking their difference. Note that energy is a property, and the value of property does not change unless the state of the system changes. Normally the stored energy, or total energy, of a system is expressed as the sum of three separate energies. The total energy of the system, Esystem, is given as

Recall that U is the sum of the energy contained within the molecules of the system (sensible, latent, chemical and nuclear) other than the kinetic and potential energies of the system as a whole and is called the internal energy. The internal energy U is dependent on the state of the system and the mass of the system. Now the conservation of energy principle, or the first law of thermodynamics for closed systems, is written as If the system does not move with a velocity and has no change in elevation, it is called a stationary system, and the conservation of energy equation reduces to 32

Mechanisms of Energy Transfer, Ein and Eout The mechanisms of energy transfer at a system boundary are: Heat, Work, mass flow. Heat and work energy transfers across at the boundary of a closed (fixed mass) system. Open systems or control volumes have energy transfer across the control surfaces by mass flow as well as heat and work. 1. Heat Transfer, Q: Heat is energy transfer caused by a temperature difference between the system and its surroundings. When added to a system heat transfer causes the energy of a system to increase and heat transfer from a system causes the energy to decrease. Q is zero for adiabatic systems. 2. Work, W: Work is energy transfer at a system boundary could have caused a weight to be raised. When added to a system, the energy of the system increase; and when done by a system, the energy of the system decreases. W is zero for systems having no work interactions at its boundaries. 3. Mass flow, m: As mass flows into a system, the energy of the system increases by the amount of energy carried with the mass into the system. Mass leaving the system carries energy with it, and the energy of the system decreases. Since no mass transfer occurs at the boundary of a closed system, energy transfer by mass 33 is zero for closed systems.

The energy balance for a general system is where the subscript “in” and “out” denote quantities that enter and leave the system, respectively. All six quantities on the right side of the equation represent “amount”, and thus they are positive quantities. The direction of any energy transfer is described by the subscript “in” and “out”.

Expressed more compactly, the energy balance is or on a rate form, as For constant rates, the total quantities during the time interval t are related to the quantities per unit time as The energy balance may be expressed on a per unit mass basis as and in the differential forms as

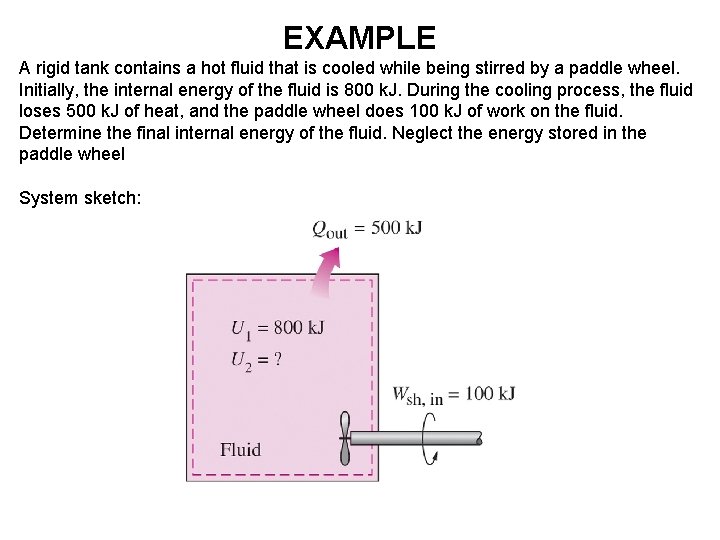
EXAMPLE A rigid tank contains a hot fluid that is cooled while being stirred by a paddle wheel. Initially, the internal energy of the fluid is 800 k. J. During the cooling process, the fluid loses 500 k. J of heat, and the paddle wheel does 100 k. J of work on the fluid. Determine the final internal energy of the fluid. Neglect the energy stored in the paddle wheel System sketch:
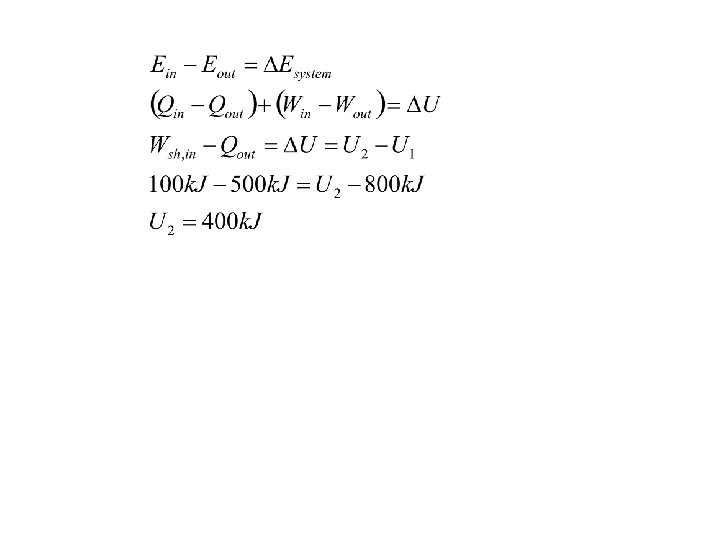

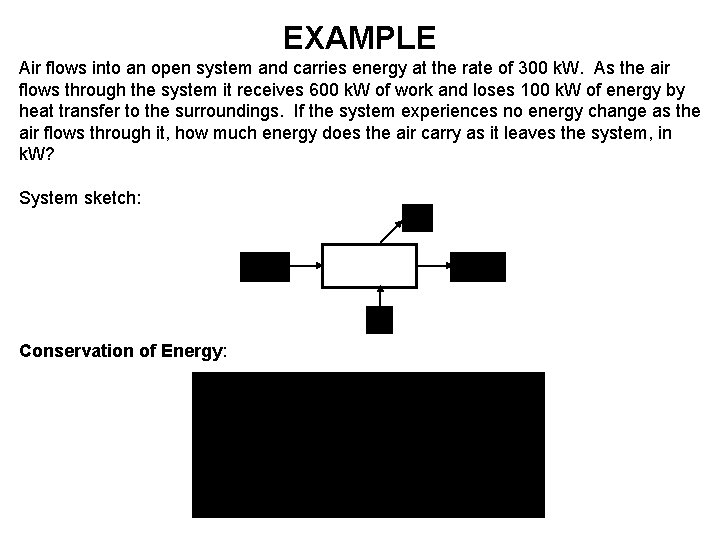
EXAMPLE Air flows into an open system and carries energy at the rate of 300 k. W. As the air flows through the system it receives 600 k. W of work and loses 100 k. W of energy by heat transfer to the surroundings. If the system experiences no energy change as the air flows through it, how much energy does the air carry as it leaves the system, in k. W? System sketch: Open System Conservation of Energy:

EXAMPLE Consider a room that is initially at the outdoor temperature of 20 o. C. The room contains a 100 -W lightbulb, a 110 -W TV set, a 200 -W refrigerator, and a 1000 -W iron. Assuming no heat transfer through the walls, determine the rate of increase of the energy content of the room when all of these electric device are on since no energy is leaving the room in any form, and thus. Also, Substituting, the rate of increase in the energy content of the room becomes

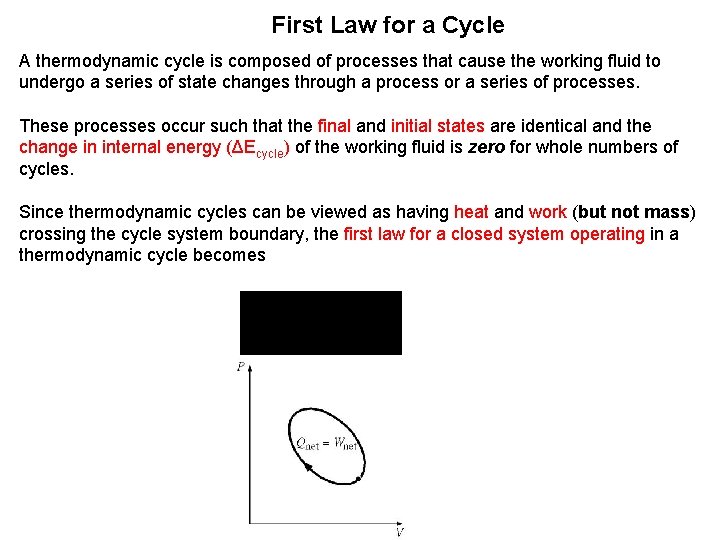
First Law for a Cycle A thermodynamic cycle is composed of processes that cause the working fluid to undergo a series of state changes through a process or a series of processes. These processes occur such that the final and initial states are identical and the change in internal energy (ΔEcycle) of the working fluid is zero for whole numbers of cycles. Since thermodynamic cycles can be viewed as having heat and work (but not mass) crossing the cycle system boundary, the first law for a closed system operating in a thermodynamic cycle becomes

EXAMPLE A steam power plant operates on a thermodynamic cycle in which water circulates through a boiler, turbine, condenser, pump, and back to the boiler. For each kilogram of steam (water) flowing through the cycle, the cycle receives 2000 k. J of heat in the boiler, rejects 1500 k. J of heat to the environment in the condenser, and receives 5 k. J of work in the cycle pump. Determine the work done by the steam in the turbine, in k. J/kg. The first law requires for a thermodynamic cycle
 Energy energy transfer and general energy analysis
Energy energy transfer and general energy analysis Energy energy transfer and general energy analysis
Energy energy transfer and general energy analysis A wave is a disturbance that transfers
A wave is a disturbance that transfers General differential equation for mass transfer
General differential equation for mass transfer Skogestad half rule calculator
Skogestad half rule calculator Skogestad half rule
Skogestad half rule Diferencia entre gran plano general y plano general
Diferencia entre gran plano general y plano general Where did general lee surrender to general grant?
Where did general lee surrender to general grant? Archery objectives
Archery objectives F vs x
F vs x How does energy flow in a food web
How does energy flow in a food web Examples of mechanical wave
Examples of mechanical wave Longitudinal wave energy transfer
Longitudinal wave energy transfer Chapter 11 admission transfer and discharge
Chapter 11 admission transfer and discharge Chapter 7 heat transfer and change of phase
Chapter 7 heat transfer and change of phase Chapter 11 admission transfer and discharge
Chapter 11 admission transfer and discharge Chapter 9 admission transfer discharge and physical exams
Chapter 9 admission transfer discharge and physical exams Admission transfer discharge and physical exams
Admission transfer discharge and physical exams Body structure general survey
Body structure general survey Normal pediatric vitals by age
Normal pediatric vitals by age The general and special senses chapter 9
The general and special senses chapter 9 Chapter 6 general anatomy and physiology
Chapter 6 general anatomy and physiology Work is the transfer of energy
Work is the transfer of energy Work is a transfer of
Work is a transfer of A rhythmic disturbance that carries energy
A rhythmic disturbance that carries energy Wave transfer matter
Wave transfer matter Roles in energy transfer
Roles in energy transfer How does conduction transfer heat
How does conduction transfer heat Pyramids of energy transfer
Pyramids of energy transfer Examples of energy transfer
Examples of energy transfer Image of energy transfer
Image of energy transfer Example of heat energy
Example of heat energy Rate of energy transfer by sinusoidal waves on strings
Rate of energy transfer by sinusoidal waves on strings Energy transfer in ecosystem
Energy transfer in ecosystem Energy transfer example
Energy transfer example Maximum elastic potential energy
Maximum elastic potential energy Sankey diagram for one bounce of a ball answers
Sankey diagram for one bounce of a ball answers Energy transferred equation
Energy transferred equation Trophic efficiency
Trophic efficiency Comic strip energy transformation
Comic strip energy transformation Limitations of remote sensing
Limitations of remote sensing A wave transfers energy without transferring
A wave transfers energy without transferring