Kinetic and Potential Energy Potential Energy An object

Kinetic and Potential Energy

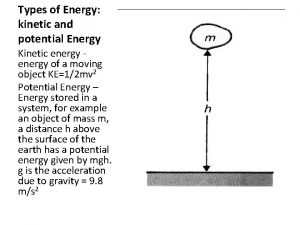
Potential Energy An object can have potential energy by virtue of its surroundings. Familiar examples of potential energy: • A wound-up spring • A stretched elastic band • An object at some height above the ground

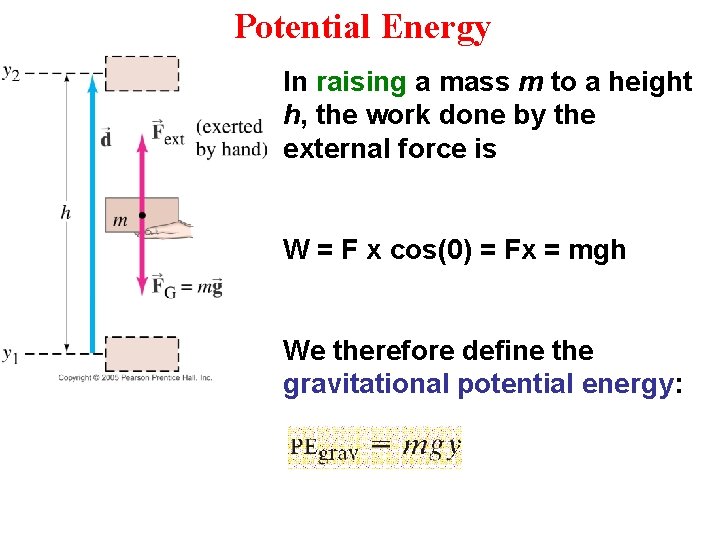
Potential Energy In raising a mass m to a height h, the work done by the external force is W = F x cos(0) = Fx = mgh We therefore define the gravitational potential energy:

Concept Question Is it possible for the gravitational potential energy of an object to be negative? 1) No. 2) Yes. 3) Maybe.

Concept Question Is it possible for the gravitational potential energy of an object to be negative? 1) No. 2) Yes. 3) Maybe. Gravitational PE is mgh, mgh where height h is measured relative to some arbitrary reference level where PE = 0. 0 For example, a book on a table has positive PE if the zero reference level is chosen to be the floor. However, if the ceiling is the zero level, level then the book has negative PE on the table It is only differences (or changes) in PE that have any physical meaning.

Potential Energy This potential energy can become kinetic energy if the object is dropped. Potential energy is a property of a system as a whole, not just of the object (because it depends on external forces). If , where do we measure y from? It turns out not to matter, as long as we are consistent about where we choose y = 0. Only changes in potential energy can be measured. CHAPTER 11 # 44, 46, 48 & 50.

Concep Question 3 You and your friend both solve a problem involving a skier going down a slope, starting from rest. The two of you have chosen different levels for y = 0 in this problem. Which of the following quantities will you and your friend agree on? A) skier’s PE 1) only B 2) only C 3) A, B, and C 4) only A and C 5) only B and C B) skier’s change in PE C) skier’s final KE

Concep Question 3 You and your friend both solve a problem involving a skier going down a slope, starting from rest. The two of you have chosen different levels for y = 0 in this problem. Which of the following quantities will you and your friend agree on? A) skier’s PE 1) only B 2) only C 3) A, B, and C 4) only A and C 5) only B and C B) skier’s change in PE C) skier’s final KE The gravitational PE depends upon the reference level, level but the difference ΔPE does not! not The work done by gravity must be the same in the two solutions, so ΔPE and ΔKE should be the same

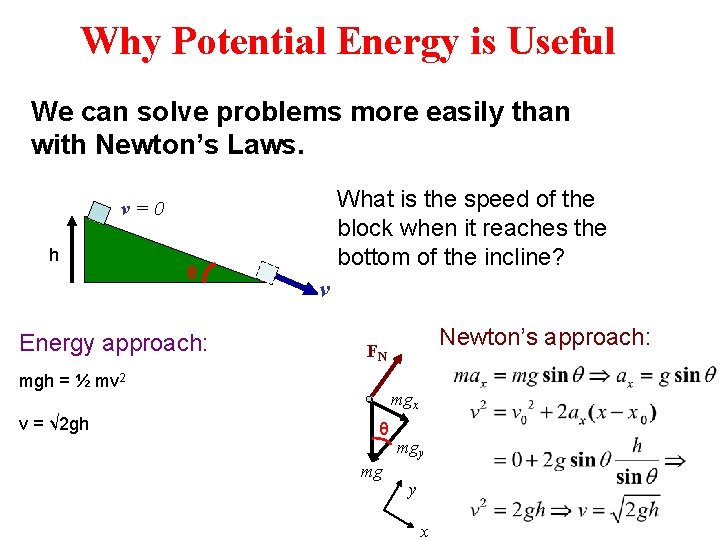
Why Potential Energy is Useful We can solve problems more easily than with Newton’s Laws. What is the speed of the block when it reaches the bottom of the incline? v=0 h θ Energy approach: v mgh = ½ mv 2 v = √ 2 gh Newton’s approach: FN mgx θ mg mgy y x

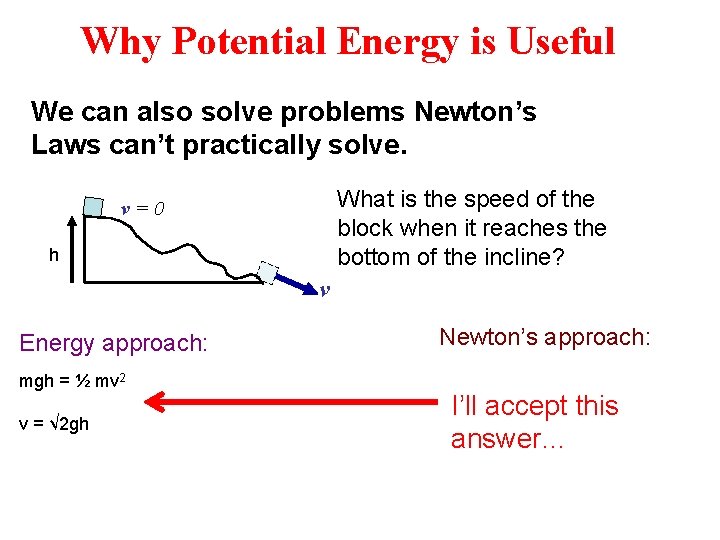
Why Potential Energy is Useful We can also solve problems Newton’s Laws can’t practically solve. What is the speed of the block when it reaches the bottom of the incline? v=0 h v Energy approach: mgh = ½ mv 2 v = √ 2 gh Newton’s approach: I’ll accept this answer…

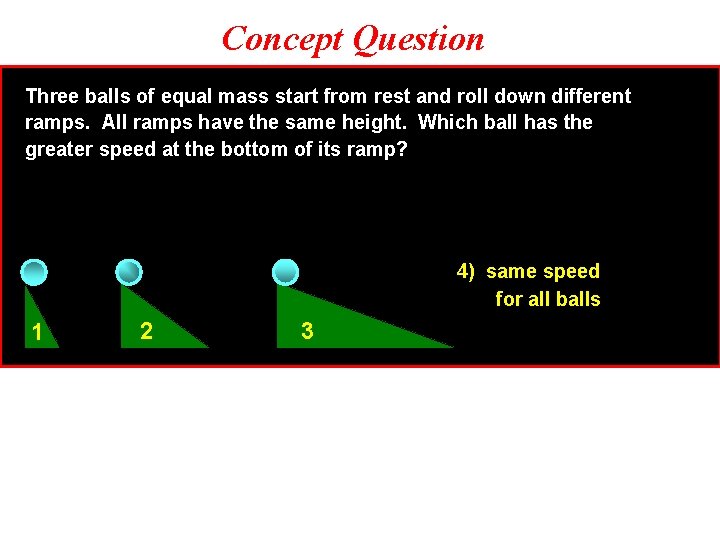
Concept Question Three balls of equal mass start from rest and roll down different ramps. All ramps have the same height. Which ball has the greater speed at the bottom of its ramp? 4) same speed for all balls 1 2 3

Concept Question Three balls of equal mass start from rest and roll down different ramps. All ramps have the same height. Which ball has the greater speed at the bottom of its ramp? 4) same speed for all balls 1 2 3 All of the balls have the same initial gravitational PE, PE since they are all at the same height (PE = mgh). Thus, when they get to the bottom, they all have the same final KE, KE and hence the same speed (KE = 1/2 mv 2). Follow-up: Which ball takes longest to get down the ramp?

Potential Energy Potential energy can also be stored in a spring when it is compressed; the figure below shows potential energy yielding kinetic energy.

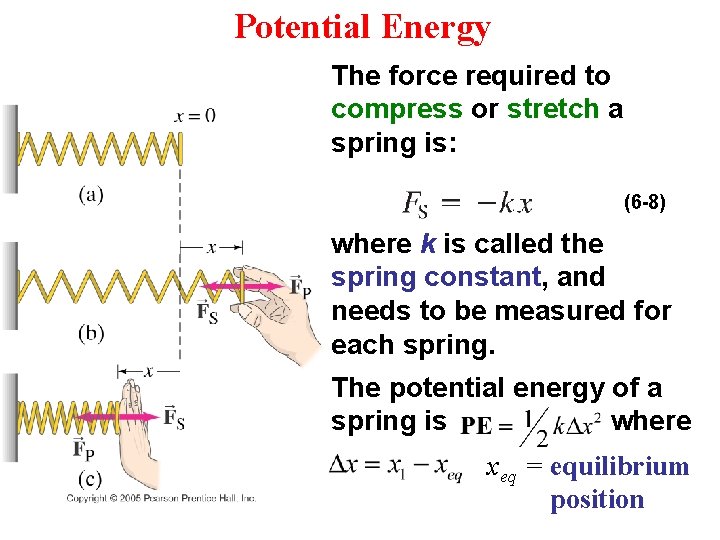
Potential Energy The force required to compress or stretch a spring is: (6 -8) where k is called the spring constant, and needs to be measured for each spring. The potential energy of a spring is where xeq = equilibrium position

Applying Potential Energy to Problems 1. By how much does the gravitational potential energy of a 64 -kg pole vaulter change if her center of mass rises about 4. 0 m during the jump?

Applying Potential Energy to Problems A 1. 60 -m tall person lifts a 2. 10 -kg book from the ground so it is 2. 20 m above the ground. What is the potential energy of the book relative to (a) the ground, and (b) the top of the person’s head? (c) How is the work done by the person related to the answers in parts (a) and (b)?

Applying Potential Energy to Problems A 1. 60 -m tall person lifts a 2. 10 -kg book from the ground so it is 2. 20 m above the ground. What is the potential energy of the book relative to (a) the ground, and (b) the top of the person’s head? (c) How is the work done by the person related to the answers in parts (a) and (b)? (a) Relative to the ground, the PE is given by b) Relative to the top of the person’s head, the PE is given by c) The work done by the person in lifting the book from the ground to the final height is the same as the answer to part (a), 45. 3 J. In part (a), the PE is calculated relative to the starting location of the application of the force on the book. The work done by the person is not related to the answer to part (b).

Energy Ball Toss Lab

Energy Conservation • Define • Equation

Sample # 1 • Rock falling from cliff

Sample # 2 • Spring on table pushes object which falls to ground. Find v at ground.

More fun problems • CHAPTER 11 # 28, 31, 34, 55, 56, 59, 64, 65 & 66.