Potential Energy and Energy Conservation Kinetic Energy Energy














- Slides: 16

Potential Energy and Energy Conservation Kinetic Energy: Energy associated with motion K = ½ mv 2 Work done by a force on an object is that forces contribution to DK may only depend upon initial and final position of object Conservative Forces Work expressed as change in Potential Energy Phys 211 C 7 p 1

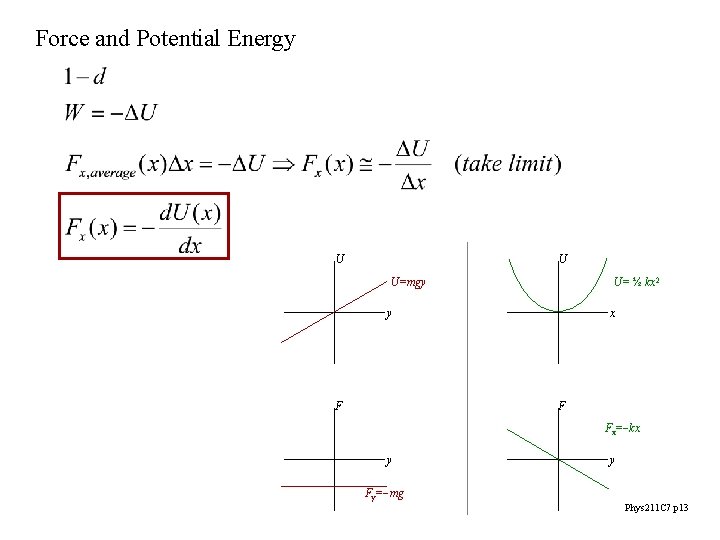
Gravitational Potential Energy Work done by gravity: Dy force × portion of displacement along force is always vertical => work = weight* height lifted d. W = F. dl = -mg dy accumulated work by force of gravity W = mg(y 1 – y 2) = mgy 1 – mgy 2 = – D(mgy) dl Dy w Note: work done does not depend upon path! Identify potential energy: U mgy W = – DU Work comes at the expense of potential energy. Phys 211 C 7 p 2

Conservation of Mechanical Energy (with gravity) In the absence of any other forces W = DK now (work energy theorem) W = - DU so DK = - DU or DK + DU = 0 Define total Energy so E=K+U DE = 0 or E 1 = E 2 In the absence of other forces, total energy is conserved! With other forces, the other forces still do work: DE = Wother Phys 211 C 7 p 3

Example: A. 145 kg baseball is thrown straight up into the air with an initial speed of 20 m/s. Determine kinetic, potential and total energy at the ball’s initial height as well as when the ball reaches its maximum height. Example, Projectile Motion: Show that two balls launched at different angles, but with the same initial speed, will have the same speed at a given height h. Use energy methods to relate the maximum height of a projectile to its initial speed and direction. Phys 211 C 7 p 4

Example, Projectile Motion: Use energy methods to relate the maximum height of a projectile to its initial speed and direction. . Example: An object of mass m slides down a semicircular frictionless ramp of radius R starting from rest. Find the speed and the normal force at the bottom of the ramp Phys 211 C 7 p 5

Example: A 12 kg crate is slid up a 2. 5 m long ramp inclined at 30°. The crate is given an initial velocity of 5. 00 m/s up the ramp, but only makes it 1. 6 m up the ramp before sliding downward. How much work is done by friction on the upward slide? How fast is the crate moving as it slides back to the bottom of the ramp? Phys 211 C 7 p 6

Elastic Potential Energy from last chapter: work done on spring W = ½ kx 22 - ½ kx 12 work done by spring Wel = ½ kx 12 - ½ kx 22 Þ elastic potential energy W = - DU U = ½ kx 2 note: x is always measured from equilibrium! another contribution to total energy DE = Wother Phys 211 C 7 p 7

Example: A 0. 200 kg mass rides on a horizontal frictionless surface, attached to a spring with a force constant of 5. 00 N/m. The mass is pulled. 100 m from equilibrium. What is the speed of the mass when it is. 080 m from equilibrium? What is the speed of the mass when it is at equilibrium? With the same mass-spring system above, a constant force of. 610 N is applied to the mass which is initially at rest at the equilibrium position. What is the glider’s speed when it has reached x =. 100 m? If the force is turned off at x =. 100 m, how much further does the mass go? Phys 211 C 7 p 8

Example: A 2000 Kg elevator is falling at a speed of 25. 0 m/s when it “bottoms out” on a spring at the bottom of the elevator shaft. The spring is supposed to stop the elevator, compressing 3. 00 m to bring it to rest. During this breaking process, a safety clamp provides a constant 17, 000 N frictional force on the elevator. What is the spring constant? What is the upward acceleration of the elevator just after it comes to a rest? Phys 211 C 7 p 9

For a Conservative Force Work can always be expressed as a change in potential energy Is reversible (Wab = -Wba) Is independent of the path of the object Does no work when the initial and final positions of the object are the same Phys 211 C 7 p 10

Example: A 40. 0 kg object with a coefficient of kinetic friction of 0. 200 may be dragged across a room by two paths: a direct 2. 5 m path, and dogleg path of 2. 00 m on the first leg and 1. 50 m along the second leg. How much work is done dragging the object across each path? Phys 211 C 7 p 11

In a closed system, energy is conserved! “loss” (or gain) of energy associated with the change of state of the materials is due to changes in Internal Energy change of temperature, melting/freezing, etc. (Thermodynamics) can be understood in terms of microscopic kinetic and potential energy (Statistical Mechanics) DE = DK + DUint = 0 Phys 211 C 7 p 12

Force and Potential Energy U U U=mgy U= ½ kx 2 y x F F Fx=-kx y y Fy=-mg Phys 211 C 7 p 13

Force and Potential Energy Phys 211 C 7 p 14

2 -d example Phys 211 C 7 p 15

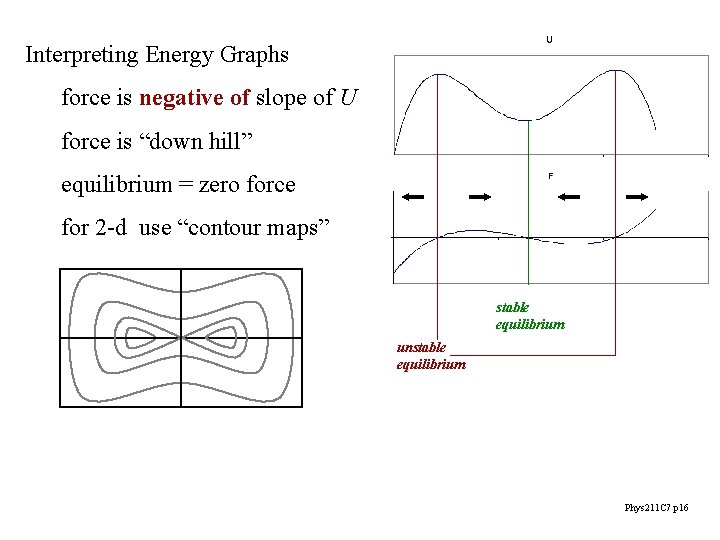
Interpreting Energy Graphs force is negative of slope of U force is “down hill” equilibrium = zero force for 2 -d use “contour maps” stable equilibrium unstable equilibrium Phys 211 C 7 p 16