ENERGY CONVERSION ES 832 a Eric Savory www









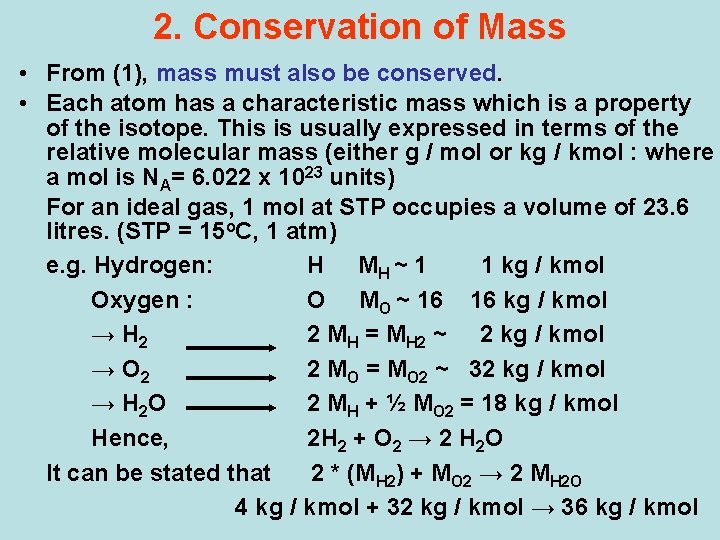














- Slides: 25

ENERGY CONVERSION ES 832 a Eric Savory www. eng. uwo. ca/people/esavory/es 832. htm Lecture 6 – Basics of combustion Department of Mechanical and Material Engineering University of Western Ontario

Fundamental Concepts of Combustion Theory • The first step in any conversion system is to determine the amount of energy which will be available for conversion. For combustion processes, this information is important for determining the necessary mass rates and the temperatures of the products entering a turbine. • Recall that a turbine is normally designed for a specific point of operation. By far, combustion is still the most common form of energy generation.

Combustion Theory • Determine the products of combustion: e. g 2 H 2 + O 2 → 2 H 2 O • Determine the heat released by combustion and the temperature of the products. • Energy balance: internal energy and enthalpy Q = UP 0 – UR 0 = ∆U = ∆Ho if K. E. negligible. • Determine the energy available for conversion.

Combustion processes (1) • EXOTHERMIC (produces heat) reactions where mass is conserved. • Most combustion processes use oxygen as oxidant (to burn with). • The substances used before the reaction are known as REACTANTS and those arising from the process are referred to PRODUCTS. • The substance undergoing oxidation is known as a FUEL. • STOICHIOMETRIC mixtures are where the air mass available is exactly that required for combustion. • EXCESS air is the amount of air present above stoichiometric ratios.

Combustion processes (2) PRINCIPAL CONSERVATION LAWS: 1. The number of atoms is conserved. 2. Mass is conserved.

Relative atomic mass of some common elements Element name Symbol Oxygen O Relative atomic mass 16 Nitrogen N 14 Hydrogen H 1 Carbon C 12 Sulphur S 32 Defined so that the element’s mass is scaled such that Carbon-12 is exactly 12.

Relative molecular mass of common substances Name Oxygen Nitrogen Hydrogen Water / steam Carbon dioxide Carbon monoxide Sulphur dioxide Symbol O 2 N 2 H 2 O CO 2 CO SO 2 Relative molecular mass 32 28 2 18 44 28 64 = mass of one molecule of that substance, relative to 1/12 th the mass of one atom of Carbon-12 Molar mass M ≈ relative molecular mass, numerically, but has units of kg / kmol

1. Conservation of atoms • Substances consist of atoms in combinations called molecules. The atoms recombine during chemical reactions, but their number remains unchanged. • Example: Combustion of hydrogen: element Hydrogen (H): molecule H 2 + element Oxygen (O): molecule O 2 Water : molecule H 2 O Reactants Products n. H 2 + m. O 2 → H 2 O ; n, m = # of molecules

To balance the reaction the number of atoms remain the same (mathematically): Hydrogen 2 n=2→n=1 Oxygen 2 m=1→m=½ Hence, H 2 + ½ O 2 → H 2 O This could also be written 2 H 2 + O 2 → 2 H 2 O (or any multiple !!)
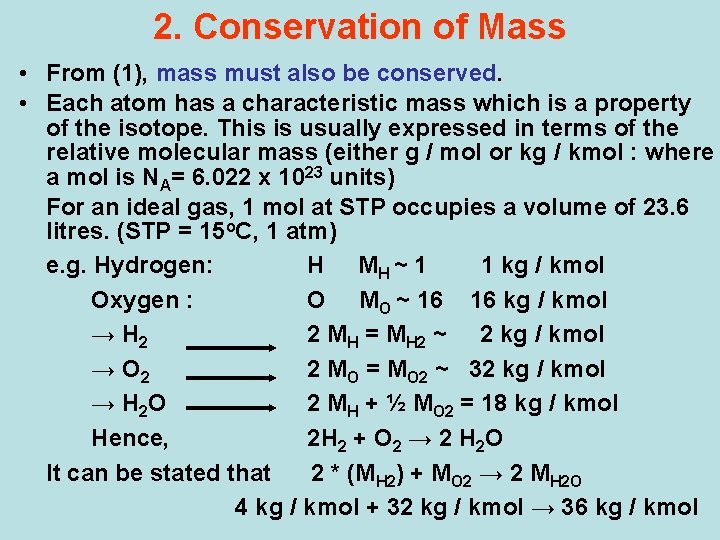
2. Conservation of Mass • From (1), mass must also be conserved. • Each atom has a characteristic mass which is a property of the isotope. This is usually expressed in terms of the relative molecular mass (either g / mol or kg / kmol : where a mol is NA= 6. 022 x 1023 units) For an ideal gas, 1 mol at STP occupies a volume of 23. 6 litres. (STP = 15 o. C, 1 atm) e. g. Hydrogen: H MH ~ 1 1 kg / kmol Oxygen : O MO ~ 16 16 kg / kmol → H 2 2 MH = MH 2 ~ 2 kg / kmol → O 2 2 MO = MO 2 ~ 32 kg / kmol → H 2 O 2 MH + ½ MO 2 = 18 kg / kmol Hence, 2 H 2 + O 2 → 2 H 2 O It can be stated that 2 * (MH 2) + MO 2 → 2 MH 2 O 4 kg / kmol + 32 kg / kmol → 36 kg / kmol

Example • Calculate the mass of oxygen required to burn 1 m 3 of fuel propane at STP. How much air must be supplied (at STP)? • Solution: (a) Need m. O 2 required to burn 1 m 3 C 3 H 8 (propane) at STP – To accomplish this task we must first determine the relative amount of reactants and products to burn the propane. This requires setting up the chemical reaction. – The next step is to determine the relative mass of each based on the ratios determined from the chemical reaction. – Then express everything in terms of 1 m 3 C 3 H 8 (propane) at STP. This will require the use of the ideal gas law (or tabled density values) for STP. – Finally, since air is used, calculate the other components based on the composition of air. (b) Set-up the primary and secondary relationships.

Calculate the relative amounts first in terms of mol: We know the products will be CO 2, H 2 O Note all products are gaseous. n C 3 H 8 + m O 2 → p CO 2 + q H 2 O for C: 3 n = p; H: 8 n = 2 q; Solving in terms of q: O: 2 m = 2 p + q q = 4 n, p = 3 n = ¾ q m = p + q/2 = 5/4 q n = q/4, m = 5/4 q, p = ¾ q Thus, for n = 1: C 3 H 8 + 5 O 2 → 3 CO 2 + 4 H 2 O

Calculate the relative mass ratios using the molar mass: Obtain molar mass for each species involved in the chemical reaction MO 2 = 32 kg / kmol; MH 2 O = 18 kg / kmol; MC = 12 kg / kmol; MH 2 = 2 kg / kmol; MC 3 H 8 = 3 MC + 4 MH 2 = 44 kg / kmol Hence, for every mol of C 3 H 8 we need 5 mol of O 2 or m. O 2/m. C 3 H 8 = 5 MO 2/1 MC 3 H 8 = (5 x 32) kg/kmol / 44 kg/kmol = 3. 636 kg. O 2 / kg. C 3 H 8 (from tables: C 3 H 8 = 2. 02 kg/m 3)

[Note: from gas constant (R): RC 3 H 8 = R / M = (8. 314 J/mol-K) / (44 kg/kmol) = 189 J/kg-K (recall: R is universal gas constant) = P / RT = (101, 300 Pa) / (189 J/kg-K) * (273 K) = 1. 97 kg/m 3 which is very close to 2. 02 kg/m 3] m. C 3 H 8 = Vol = 2. 02 kg/m 3 * 1 m 3 = 2. 02 kg m. O 2 = 3. 636 kg. O 2/kg. C 3 H 8 * 2. 02 kg. C 3 H 8 = 7. 34 kg of oxygen

Calculate the total amount of air: The molar (i. e. volumetric) ratios of air composition are approximately: N 2 = 79%; Argon (Ar) = 1% and O 2 = 20%; For every 1 m 3 of propane, we have (from the chemical equation of part (a)): 5 m 3 O 2 + 5(0. 79/0. 20)m 3 N 2 + 5(0. 01/0. 20)m 3 Ar = 25 m 3 of air. What if the ideal gas equation had been used? We would then predict 7. 16 kg of oxygen but the volume of air would remain the same.

SUMMARY: Combustion processes are exothermic reactions in which mass and energy are conserved. Molecular ratios are used to determine volumetric and mass ratios. Stoichiometric mixtures are those for which the amount of air is exactly that need for 100% combustion. Excess air is the amount of air above Stoichiometric conditions.

Internal energy and enthalpy of combustion A heat conversion system is designed to produce a desired power output. Typically, the engineer is provided with the desired output levels, the turbine thermodynamic and mechanical efficiencies and the operating point (inlet temperature and pressure). The task of the engineer then becomes to determine the amount of energy generation and the mass flow rate of products needed to achieve these conditions. To do so requires that the engineer know (i) the amount of fuel required; (ii) the amount air required to combust these fuels and the mass flow rate and temperature of the products of combustion.

Objective 1. Calculate the rate of energy which is liberated during a combustion process 2. Determine the minimum mass flow rate of air required for combustion 3. Determine the temperature and flow rate of products.

The heat released, Q, during a chemical reaction is a property of the reactants and the process. For a closed system (no-flow) one obtains: Q = (UP 2 - UP 0) + (UR 0 - UR 1) + ∆U 0 And for an open system (steady-flow): Q = (HP 2 - HP 0) + (HR 0 - HR 1) + ∆H 0 + ∆K. E. [ Subscripts: P = product; R = reactant; 0, 1, 2 = temperatures T 0, T 1 and T 2 ] (note sign convention: Q > 0 if supplied by surroundings, thus ∆U 0 < 0; ∆H 0 < 0 ) ∆U 0 and ∆H 0 are the internal energy and enthalpy of combustion, respectively. ∆K. E. is kinetic energy

The enthalpy of combustion is usually given in terms of k. J/kmol, ∆h 0, such that: ∆H 0 = n*∆h 0 where n = kmol of fuel ∆h 0: • Is a property of the reaction. It is given at a standard reference (25°C and 1 atm) • It is assumed that reactants and products are at the same temperature and pressure • If not tabulated, it can be calculated from the energy of formation, hf, of the individual chemical species at 25°C and 1 atm. ∆h 0 = ∑n*hf - ∑n*hf ; n = kmol of species/kmol fuel Products Reactants

NOTES: (1) It is important to know the phase (liquid or gas) for reactants, fuel and products since the enthalpy of vaporization, hfg, must be included if present. (2) By definition: ∆u 0 = ∆h 0 - (∑Pν ∑Pν) Products Reactants v = specific molar volume, P = pressure For most practical situations: ∆u 0 ≈ ∆h 0 and so ∆U 0 ≈ ∆H 0

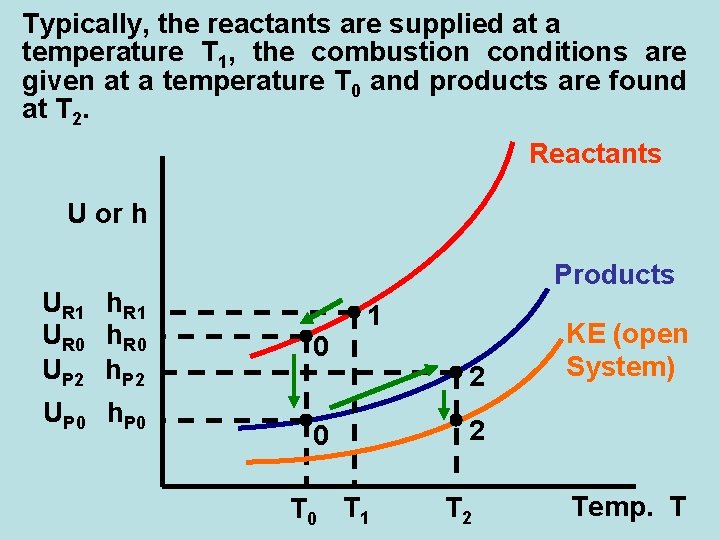
Typically, the reactants are supplied at a temperature T 1, the combustion conditions are given at a temperature T 0 and products are found at T 2. Reactants U or h UR 1 h. R 1 UR 0 h. R 0 UP 2 h. P 2 UP 0 h. P 0 Products 0 1 0 T 1 2 KE (open System) 2 Temp. T

Rigorously, the enthalpy (or internal energy) at the states 0, 1 and 2 should be obtained from the tabulated thermodynamic values. However, for most engineering design purposes a good approximation is obtained from: - 1 or where: Cv or Cp are evaluated at (T 0+T 1)/2 for reactants and (T 0+T 2)/2 for products.

Example A stoichiometric mixture of air and gaseous methane at 54 o. C and 2 bar is buried in a 0. 1 m 3 rigid vessel. The temperature of the products is measured to be 1, 529 o. C. Given that the internal energy of combustion ∆Uo = - 802, 310 k. J/kmol at 25 o. C, calculate the amount of heat rejected to the environment. Hence, information given: To = 25 o. C = 298 K ∆Uo = -802, 310 k. J/kmol T 1 = 54 o. C = 327 K P 1 = 2 bar V = 0. 1 m 3 T 2 = 1, 529 o. C = 1, 802 K Air is provided: Use 79% N 2 , 21% O 2

Summary • The total energy liberated during a chemical reaction is based on a 1 st Law of Thermodynamics balance (for either a closed or an open system). • The heat released during the reaction, ∆H 0, is a property of the reaction. • ∆H 0 is generally tabulated for a specific condition. Equations of state and the 1 st Law of thermodynamics can be used to calculate the heat release to the actual state. It can be calculated from the energy of formation of the chemical species.
 Eric savory
Eric savory Molar mass of oxygen
Molar mass of oxygen Eric savory
Eric savory Eric savory
Eric savory Eric savory
Eric savory What is the scientific notation for 832 000
What is the scientific notation for 832 000 Heather savory
Heather savory Savory parmo birmingham
Savory parmo birmingham Richard savory
Richard savory Energy conversion of a toaster
Energy conversion of a toaster Energy energy transfer and general energy analysis
Energy energy transfer and general energy analysis Energy energy transfer and general energy analysis
Energy energy transfer and general energy analysis Classification of wecs
Classification of wecs Energy transformation of electric kettle
Energy transformation of electric kettle Radiant energy examples
Radiant energy examples Microwave oven energy transformation
Microwave oven energy transformation Energy conversion and conservation
Energy conversion and conservation Example of electrical energy
Example of electrical energy Alarm clock energy conversion
Alarm clock energy conversion Transformer energy conversion
Transformer energy conversion Energy conversion table
Energy conversion table Kinetic energy definition
Kinetic energy definition How is energy like money worksheet
How is energy like money worksheet Windmill energy conversion
Windmill energy conversion Transformation of energy definition
Transformation of energy definition Investigation gagglekeierleber the
Investigation gagglekeierleber the