CHAPTER 1 BASIC CONCEPT All the programs in

CHAPTER 1 BASIC CONCEPT All the programs in this file are selected from Ellis Horowitz, Sartaj Sahni, and Susan Anderson-Freed “Fundamentals of Data Structures in C”, 1/e, Computer Science Press, 1992, 2/e, Silicon press, 2008. CHAPTER 1 1

Pointers l* ¡dereferencing operator, indirection operator l& ¡address operator l int i, *pi; l pi = &i; l *pi = 10; or i = 10; CHAPTER 1 2

Dynamic Memory Allocation l int i, *pi; l float f, *pf; l pi = (int *) malloc (sizeof(int)); l pf = (float *) malloc (sizeof(float)); l *pi = 1024; l *pf = 3. 14; l printf (“Integer = %d; float = %fn”, *pi, *pf); l free (pi); l free (pf); CHAPTER 1 3

Dynamic Memory Allocation l l l l l #define MALLOC(p, s) if (!((p) = malloc(s))) { fprintf(stderr, “Insufficient memory”); exit (EXIT_FAILURE); } …… int *pi; …… MALLOC(pi, sizeof(int)); *pi = 1024; CHAPTER 1 4


How to create programs l Requirements: What inputs, functions, and outputs l Analysis: bottom-up vs. top-down l Design: data objects and operations l Refinement and Coding l Verification ¡ Program Proving ¡ Testing ¡ Debugging CHAPTER 1 6

Algorithm l Definition An algorithm is a finite set of instructions that accomplishes a particular task. l Criteria ¡ Input: zero more quantities are externally supplied. ¡ Output: at least one quantity is produced. ¡ definiteness: clear and unambiguous ¡ finiteness: terminate after a finite number of steps ¡ effectiveness: instruction is basic enough to be carried out CHAPTER 1 7

Algorithm l One distinguishes between an algorithm and a program, the latter of which does not have to satisfy the fourth condition (Finiteness). l For example, we can think of an operating system that continues in a wait loop until more jobs are entered. CHAPTER 1 8
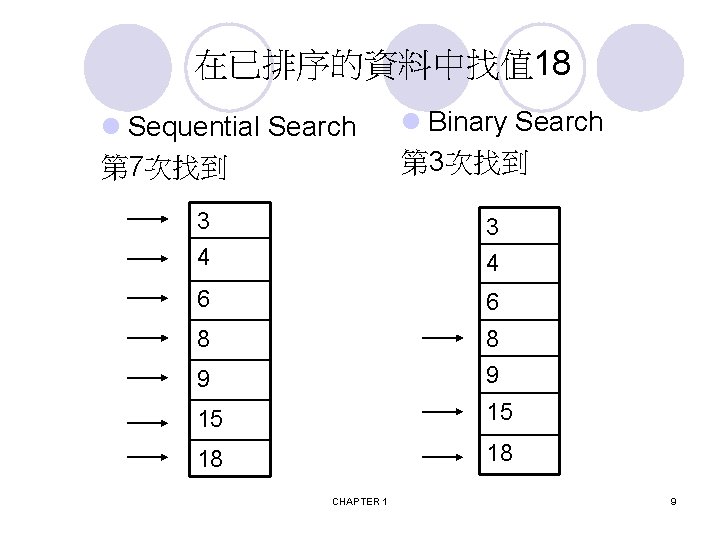
在已排序的資料中找值 18 l Sequential Search 第 7次找到 l Binary Search 第 3次找到 3 4 6 6 8 8 9 9 15 15 18 18 CHAPTER 1 9

Translating a Problem into an Algorithm l Problem ¡ Devise a program that sorts a set of n>= 1 integers l Solution I ¡ From those integers that are currently unsorted, find the smallest and place it next in the sorted list l Solution II ¡ for (i= 0; i< n; i++){ Examine list[i] to list[n-1] and suppose that the smallest integer is list[min]; Interchange list[i] and list[min]; } CHAPTER 1 10
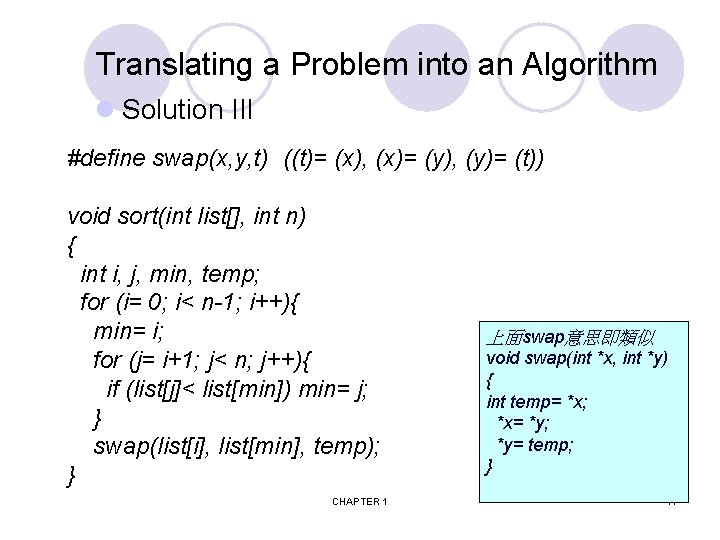
Translating a Problem into an Algorithm l Solution III #define swap(x, y, t) ((t)= (x), (x)= (y), (y)= (t)) void sort(int list[], int n) { int i, j, min, temp; for (i= 0; i< n-1; i++){ min= i; for (j= i+1; j< n; j++){ if (list[j]< list[min]) min= j; } swap(list[i], list[min], temp); } CHAPTER 1 上面swap意思即類似 void swap(int *x, int *y) { int temp= *x; *x= *y; *y= temp; } 11

Data Type l Data Type A data type is a collection of objects and a set of operations that act on those objects. l Example of "int" ¡ Objects: 0, +1, -1, . . . , Int_Max, Int_Min ¡ Operations: arithmetic(+, -, *, /, and %), testing (equality/inequality), assigns, functions CHAPTER 1 12


Abstract Data Type l Abstract Data Type An abstract data type (ADT) is a data type that is organized in such a way that the specification of the objects and the operations on the objects is separated from the representation of the objects and the implementation of the operations. l ADT Operations — only the operation name and its parameters are visible to the user — through interface l Why abstract data type ? ¡ implementation-independent l 不管如何(How)作,只管作了什麼(What) l Abstraction is … ¡ Generalization of operations with unspecified implementation CHAPTER 1 14
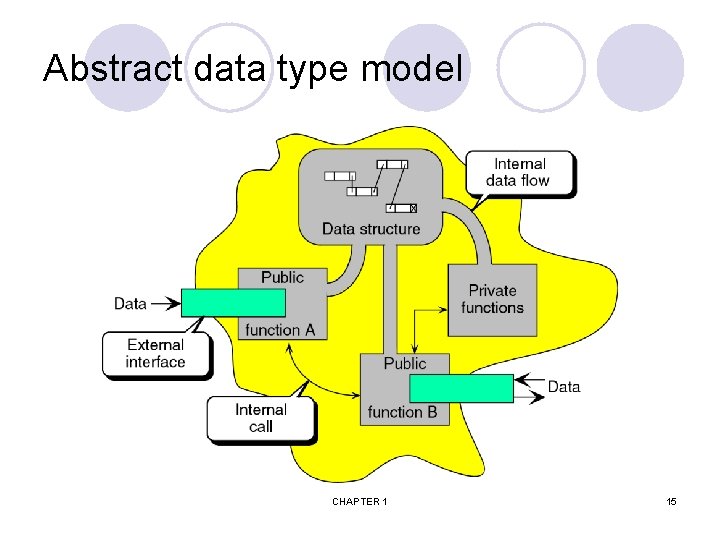
Abstract data type model CHAPTER 1 15

Classifying the Functions of a Data Type l Creator/constructor ¡ Create a new instance of the designated type l Transformers ¡ Also create an instance of the designated type by using one or more other instances l Observers/reporters ¡ Provide information about an instance of the type, but they do not change the instance CHAPTER 1 16

*ADT 1. 1: Abstract data type Natural_Number (p. 20) structure Natural_Number is (denoted by Nat_No) objects: an ordered subrange of the integers starting at zero and ending at the maximum integer (INT_MAX) on the computer functions: Creator for all x, y Nat_Number; TRUE, FALSE Boolean and where +, -, <, and == are the usual integer operations. Nat_No Zero ( ) : : = 0 Boolean Is_Zero(x) : : = if (x) return FALSE else return TRUE Observer Nat_No Add(x, y) : : = if ((x+y) <= INT_MAX) return x+y else return INT_MAX Boolean Equal(x, y) : : = if (x== y) return TRUE else return FALSE Transformer Nat_No Successor(x) : : = if (x == INT_MAX) return x else return x+1 Nat_No Subtract(x, y) : : = if (x<y) return 0 else return x-y end Natural_Number CHAPTER 1 17

Play with ADT l Add(Zero(), y) : : = return y l Add(Successor(x), y) : : = return Successor(Add(x, y)) l Equal(Zero(), Zero()) : : = return TRUE l Equal(Successor(x), Zero()) : : = return FALSE l Equal(Successor(x), Successor(y)) : : = return Equal(x, y) CHAPTER 1 18

Play with ADT (cont’d) l 0 Zero() l 1 Successor(Zero()) l 2 Successor(Zero())) l 1 + 2 = ? ¡… l 1 + 2 == 3 ? CHAPTER 1 19

Recursive Algorithms l Direct recursion ¡Functions call themselves l Indirect recursion ¡Functions call other functions that invoke the calling function again l Any function that we can write using assignment, if-else, and while statements can be written recursively. CHAPTER 1 20

Recursive algorithm l How to determine that express an algorithm recursively ? ¡ The problem itself is defined recursively ¡ Statements: if-else and while can be written recursively l How to design recursive algorithm 1. 找出遞迴關係 ¡ 找出遞迴關係才能夠對問題進行切割 2. 找出終止條件 ¡ 找出終止條件避免無窮遞迴下去 CHAPTER 1 非常重要 !! 21

![Binary Search int binsearch(int list[], int searchnum, int left, int right) {// search list[0]<= Binary Search int binsearch(int list[], int searchnum, int left, int right) {// search list[0]<=](http://slidetodoc.com/presentation_image_h/375e3b83b08e33cd592043ae1543c1a4/image-23.jpg)
Binary Search int binsearch(int list[], int searchnum, int left, int right) {// search list[0]<= list[1]<=. . . <=list[n-1] for searchnum int middle; while (left<= right){ middle= (left+ right)/2; switch(compare(list[middle], searchnum)){ case -1: left= middle+ 1; break; int compare(int x, int y) case 0: return middle; { case 1: right= middle- 1; if (x< y) return -1; else if (x== y) return 0; } } else return 1; return -1; } } CHAPTER 1 23
![Recursive Implementation of Binary Search int binsearch(int list[], int searchnum, int left, int right) Recursive Implementation of Binary Search int binsearch(int list[], int searchnum, int left, int right)](http://slidetodoc.com/presentation_image_h/375e3b83b08e33cd592043ae1543c1a4/image-24.jpg)
Recursive Implementation of Binary Search int binsearch(int list[], int searchnum, int left, int right) {// search list[0]<= list[1]<=. . . <=list[n-1] for searchnum int middle; if (left<= right){ middle= (left+ right)/2; switch(compare(list[middle], searchnum)){ case -1: return binsearch(list, searchnum, middle+1, right); case 0: return middle; case 1: return binsearch(list, searchnum, left, middle- 1); } } return -1; } CHAPTER 1 24

CHAPTER 1 26

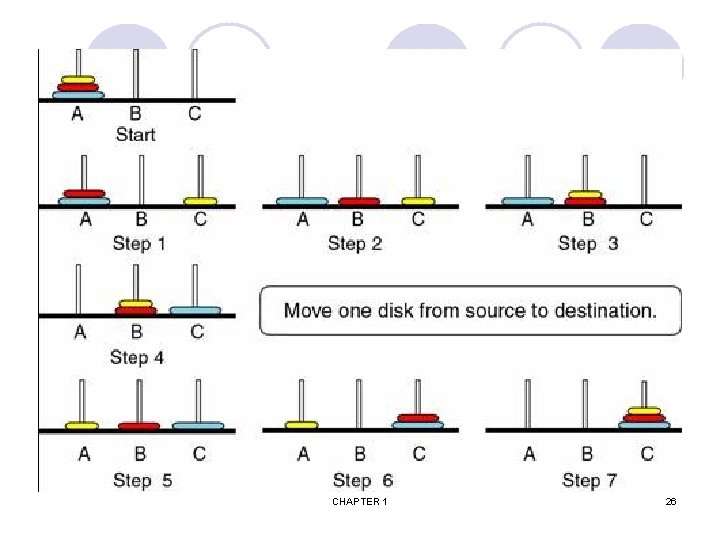
河內塔程式碼 void Hanoi(int n, char x, char y, char z) { if (n > 1) { Hanoi(n-1, x, z, y); printf("Move disk %d from %c to %c. n", n, x, z); Hanoi(n-1, y, x, z); } else { printf("Move disk %d from %c to %c. n", n, x, z); } } CHAPTER 1 27

Hanoi (n , x , y , z) n=4 的結果 執行 Hanoi(3, x, z, y). 執行 Hanoi(2, x, y, z). 執行 Hanoi(1, x, z, y). 列印 Move disk 1 from x to y. 列印 Move disk 2 from x to z. 執行 Hanoi(1, y, x, z). 列印 Move disk 1 from y to z. 列印 Move disk 3 from x to y. 執行 Hanoi(2, z, x, y). 執行 Hanoi(1, z, y, x). 列印 Move disk 1 from z to x. 列印 Move disk 2 from z to y. CHAPTER 1 28

執行 Hanoi(1, x, z, y). 列印 Move disk 1 from x to y. 列印 Move disk 4 from x to z. 執行 Hanoi(3, y, x, z). 執行 Hanoi(2, y, z, x). 執行 Hanoi(1, y, x, z). 列印 Move disk 1 from y to z. 列印 Move disk 2 from y to x. 執行 Hanoi(1, z, y, x) 列印 Move disk 1 from z to x. 列印 Move disk 3 from y to z. 執行 Hanoi(2, x, y, z). 執行 Hanoi(1, x, z, y). 列印 Move disk 1 from x to y. 列印 Move disk 2 from x to z. 執行 Hanoi(1, y, x, z). 列印 Move disk 1 from y to z. CHAPTER 1 29

Performance Analysis (machine independent) l Space and Time ¡ Does the program efficiently use primary and secondary storage? ¡ Is the program's running time acceptable for the task? l Evaluate a program generally ¡ Does the program meet the original specifications of the task? ¡ Does it work correctly? ¡ Does the program contain documentation that show to use it and how it works? ¡ Does the program effectively use functions to create logical units? ¡ Is the program's code readable? CHAPTER 1 30
Performance Analysis(Cont. ) Practice l Evaluate a program Meet specifications, Work correctly, Good user-interface, Well-documentation, Readable, Effectively use functions, Running time acceptable, Efficiently use space/storage l How to achieve them? ¡ Good programming style, experience, and practice ¡ Discuss and think Think CHAPTER 1 31

S(P)= c+ Sp(I) l The space needed is the sum of P: a program I: instance (input, output) ¡Fixed space and Variable space l Fixed space: c ¡Includes the instructions, variables, and constants ¡Independent of the number and size of I/O l Variable space: Sp(I) ¡Includes dynamic allocation, functions' recursion l Total space of any program ¡S(P)= c+ Sp(Instance) CHAPTER 1 32

*Program 1. 10: Simple arithmetic function (p. 23) float abc(float a, float b, float c) { return a + b * c + (a + b - c) / (a + b) + 4. 00; } Sabc(I) = 0 *Program 1. 11: Iterative function for summing a list of numbers (p. 24) float sum(float list[ ], int n) { float tempsum = 0; int i; for (i = 0; i<n; i++) tempsum += list [i]; return tempsum; } Ssum(I) = 0 Recall: pass the address of the first element of the array & pass by value CHAPTER 1 33

*Program 1. 12: Recursive function for summing a list of numbers (p. 24) float rsum(float list[ ], int n) { if (n) return rsum(list, n-1) + list[n-1]; return 0; } Ssum(I)=Ssum(n)=6 n *Figure 1. 1: Space needed for one recursive call of Program 1. 11 (p. 25) (以 16 bit x 86 small/near為例) * CHAPTER 1 34

Time Complexity q Total time q T(P)= compile time + run (or execution) time q May run it many times without recompilation. Run time q How to evaluate? q + - * / … (最細的估計) q Use the system clock 直接用量的比較省事 q Number of steps performed (中等的估計) qmachine-independent q. Instance及所費時間函數的趨勢 (粗略的估計, p. 33) q Definition of a program step q A program step is a syntactically or semantically meaningful program segment whose execution time is independent of the instance characteristics CHAPTER 1 35

Methods to compute the step count l Introduce variable count into programs l Tabular method ¡ Determine the total number of steps contributed by each statement l steps_per_statement * frequency_for_that_statement l s/e, steps/execution ¡ add up the contribution of all statements CHAPTER 1 36

Iterative summing of a list of numbers *Program 1. 13: Program 1. 11 with count statements (p. 26) float sum(float list[ ], int n) { float tempsum = 0; count++; /* for assignment */ int i; for (i = 0; i < n; i++) { count++; /*for the for loop */ tempsum += list[i]; count++; /* for assignment */ } count++; /* last execution of for */ count++; /* for return */ return tempsum; } CHAPTER 1 2 n + 3 steps 37
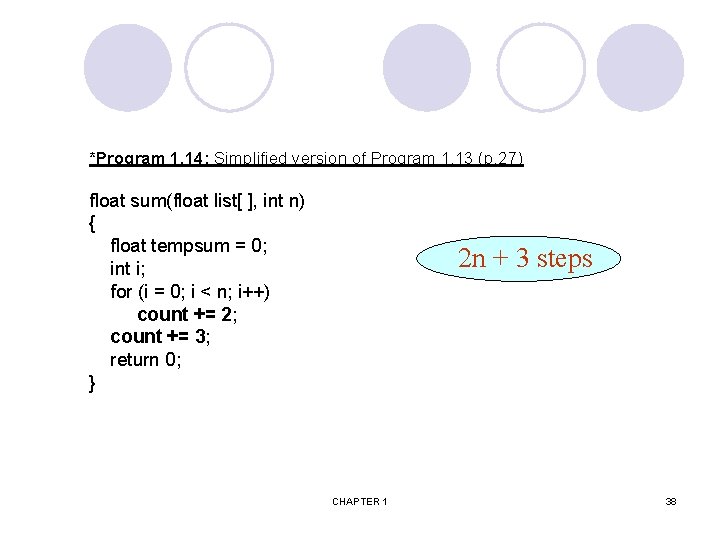
*Program 1. 14: Simplified version of Program 1. 13 (p. 27) float sum(float list[ ], int n) { float tempsum = 0; int i; for (i = 0; i < n; i++) count += 2; count += 3; return 0; } 2 n + 3 steps CHAPTER 1 38

Recursive summing of a list of numbers *Program 1. 15: Program 1. 12 with count statements added (p. 27) float rsum(float list[ ], int n) { count++; /*for if conditional */ if (n) { count++; /* for return and rsum invocation */ return rsum(list, n-1) + list[n-1]; } count++; return list[0]; } 2 n+2 steps CHAPTER 1 39
![Matrix addition *Program 1. 16: Matrix addition (p. 28) void add( int a[ ] Matrix addition *Program 1. 16: Matrix addition (p. 28) void add( int a[ ]](http://slidetodoc.com/presentation_image_h/375e3b83b08e33cd592043ae1543c1a4/image-40.jpg)
Matrix addition *Program 1. 16: Matrix addition (p. 28) void add( int a[ ] [MAX_SIZE], int b[ ] [MAX_SIZE], int c [ ] [MAX_SIZE], int rows, int cols) { int i, j; for (i = 0; i < rows; i++) for (j= 0; j < cols; j++) c[i][j] = a[i][j] +b[i][j]; } CHAPTER 1 40
![*Program 1. 17: Matrix addition with count statements (p. 29) void add(int a[ ][MAX_SIZE], *Program 1. 17: Matrix addition with count statements (p. 29) void add(int a[ ][MAX_SIZE],](http://slidetodoc.com/presentation_image_h/375e3b83b08e33cd592043ae1543c1a4/image-41.jpg)
*Program 1. 17: Matrix addition with count statements (p. 29) void add(int a[ ][MAX_SIZE], int b[ ][MAX_SIZE], int c[ ][MAX_SIZE], int row, int cols ) { int i, j; for (i = 0; i < rows; i++){ count++; /* for i for loop */ 2 rows * cols for (j = 0; j < cols; j++) { count++; /* for j for loop */ c[i][j] = a[i][j] + b[i][j]; count++; /* for assignment statement */ } count++; /* last time of j for loop */ } count++; /* last time of i for loop */ } CHAPTER 1 + 2 rows + 1 41
![*Program 1. 18: Simplification of Program 1. 17 (p. 29) void add(int a[ ][MAX_SIZE], *Program 1. 18: Simplification of Program 1. 17 (p. 29) void add(int a[ ][MAX_SIZE],](http://slidetodoc.com/presentation_image_h/375e3b83b08e33cd592043ae1543c1a4/image-42.jpg)
*Program 1. 18: Simplification of Program 1. 17 (p. 29) void add(int a[ ][MAX_SIZE], int b [ ][MAX_SIZE], int c[ ][MAX_SIZE], int rows, int cols) { int i, j; for( i = 0; i < rows; i++) { for (j = 0; j < cols; j++) count += 2; } count++; 2 rows cols + 2 rows } +1 Suggestion: Interchange the loops when rows >> cols CHAPTER 1 42

Tabular Method Iterative function to sum a list of numbers *Figure 1. 2: Step count table for Program 1. 11 (p. 30) steps/execution CHAPTER 1 43

Recursive Function to sum of a list of numbers *Figure 1. 3: Step count table for recursive summing function (p. 31) CHAPTER 1 44

Matrix Addition *Figure 1. 4: Step count table for matrix addition (p. 31) CHAPTER 1 45

Asymptotic Notation(O, , ) l Exact step count ¡ Compare the time complexity of two programs that computing the same function ¡ Difficult task of most of programs l Asymptotic notation ¡ Big “oh” lupper bound(current trend) ¡ Omega llower bound ¡ Theta lupper and lower bound CHAPTER 1 46

Asymptotic Notation O l Definition ¡ f(n)= O(g(n)) iff there exist positive constants c and n 0 such that f(n)<= cg(n) for all n, n>= n 0 l Examples ¡ 3 n+ 2= O(n) as 3 n+ 2<= 4 n for all n>= 2 ¡ 10 n 2+ 4 n+ 2= O(n 2) as 10 n 2+ 4 n+ 2<= 11 n 2 for n>= 5 ¡ 3 n+2<> O(1), 10 n 2+ 4 n+ 2<> O(n) l Remarks ¡ g(n) is upper bound, the least? (估algorithm, 作答時 …) ln=O(n 2)=O(n 2. 5)= O(n 3)= O(2 n) ¡ O(1): constant, O(n): linear, O(n 2): quadratic, O(n 3): cubic, and O(2 n): exponential (各舉一例) CHAPTER 1 47

Asymptotic Notation l Definition ¡ f(n)= (g(n)) iff there exist positive constants c and n 0 such that f(n)>= cg(n) for all n, n>= n 0 l Examples ¡ 3 n+ 2= (n) as 3 n+ 2>= 3 n for n>= 1 ¡ 10 n 2+ 4 n+ 2= (n 2) as 10 n 2+4 n+ 2>= n 2 for n>= 1 ¡ 6*2 n+ n 2= (2 n) as 6*2 n+ n 2 >= 2 n for n>= 1 l Remarks ¡ lower bound, the largest ? (used for problem) l 3 n+3= (1), 10 n 2+4 n+2= (n); 6*2 n+ n 2= (n 100) l Theorem ¡ If f(n)= amnm+. . . + a 1 n+ a 0 and am> 0, then f(n)= (nm) CHAPTER 1 48

Asymptotic Notation l Definition ¡ f(n)= (g(n)) iff there exist positive constants c 1, c 2, and n 0 such that c 1 g(n)<= f(n) <= c 2 g(n) for all n, n>= n 0 l Examples ¡ 3 n+2= (n) as 3 n+2>=3 n for n>1 and 3 n+2<=4 n for all n>= 2 ¡ 10 n 2+ 4 n+ 2= (n 2); 6*2 n+n 2= (2 n) l Remarks ¡ Both an upper and lower bound ¡ 3 n+2!= (1); 10 n 2+4 n+ 2!= (n) l Theorem ¡ If f(n)= amnm+. . . +a 1 n+ a 0 and am> 0, then f(n)= (nm) CHAPTER 1 49
![Example of Time Complexity Analysis Statement Asymptotic complexity void add(int a[][Max. . . . Example of Time Complexity Analysis Statement Asymptotic complexity void add(int a[][Max. . . .](http://slidetodoc.com/presentation_image_h/375e3b83b08e33cd592043ae1543c1a4/image-50.jpg)
Example of Time Complexity Analysis Statement Asymptotic complexity void add(int a[][Max. . . . ) { int i, j; for(i= 0; i< rows; i++) for(j=0; j< cols; j++) c[i][j]= a[i][j]+ b[i][j]; } 0 0 0 (rows) (rows*cols) 0 Total (rows*cols) CHAPTER 1 50
![Example of Time Complexity Analysis(Cont. ) int binsearch(int list[], int left, int right) { Example of Time Complexity Analysis(Cont. ) int binsearch(int list[], int left, int right) {](http://slidetodoc.com/presentation_image_h/375e3b83b08e33cd592043ae1543c1a4/image-51.jpg)
Example of Time Complexity Analysis(Cont. ) int binsearch(int list[], int left, int right) { int middle; while (left<= right){ middle= (left+ right)/2; switch(compare(list[middle], searchnum)){ case -1: left= middle+ 1; break; worst case (log n) case 0: return middle; best case (1) case 1: right= middle- 1; } } return -1; } CHAPTER 1 51

*Figure 1. 9: Times on a 1 billion instruction per second computer(p. 44) CHAPTER 1 52
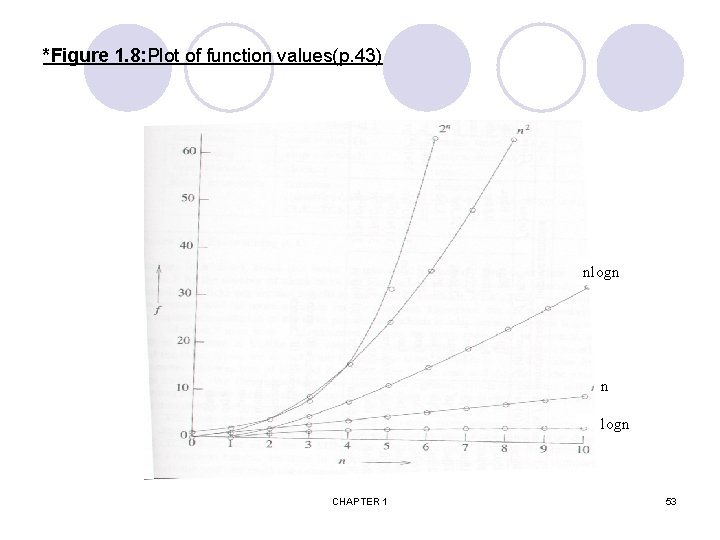
*Figure 1. 8: Plot of function values(p. 43) nlogn n logn CHAPTER 1 53

Performance Measurement (machine dependent) ¡ 注意: 一般常以 average case 和 worst case 來討論 (真的要怎麼作? ) l Estimate average case : 用隨機的測試資料, 取結果的平均時間 l Estimate worst case : 用隨機的測試資料, 取結果的最大時間 ¡ There actually two different methods for timing events in C. l Figure 1. 10 shows the major differences between these two methods. l Method 1 uses clock to time events. This function gives the amount of processor time that has elapsed since the program began running. l Method 2 uses time to time events. This function returns the time, measured in seconds, as the built-in type time_t. l The exact syntax of the timing functions varies from computer to computer and also depends on the operating system and compiler in use. Method 1 Figure 1. 10 Start timing start=clock(); start=time(NULL); Stop timing stop=clock(); stop=time(NULL); Type returned clock_t time_t Result in seconds duration=((double)(stopstart)/CLK_TCK; duration=(double)difftime(st op, start); CHAPTER 1 CLOCKS_PER_ SEC Method 2 54
- Slides: 54