Thermal Physics Topic 3 1 Thermal Concepts Temperature






















































- Slides: 72

Thermal Physics Topic 3. 1 Thermal Concepts

Temperature – Macroscopic • At a macroscopic level, temperature is the degree of hotness or coldness of a body as measured by a thermometer • Temperature is a property that determines the direction of thermal energy transfer (heat) between two bodies in contact • Temperature is measured in degrees Celsius (o. C) or Kelvin (K) – Where Temp in K = Temp in o. C + 273 – Temp in K is known as the absolute temperature

DIFFERENCE BETWEEN HEAT AND THERMAL ENERGY Thermal energy is a term often confused with that of heat. Simply put, heat is the flow of thermal energy. Thermal energy is the total internal energy of the system. This has to do Thermal energy is the total internal energy of the system with the kinetic and potential energies of the molecules, i. e. how fast the molecules are vibrating and their chemical bonds. Heat goes from objects with high temperature to low temperature, not high thermal energy to low thermal energy. For example, a massive glacier will have more total thermal energy than a small hot nail (simply because it has more molecules); however, its temperature is lower because it has less average thermal energy. Therefore, energy will be transferred from the nail to the glacier. . . Heat will not flow between two bodies of the same temperature Heat transfer = energy transfer

Thermal Equilibrium • When 2 bodies are placed in contact heat will flow from the body at higher temp to the body with lower temp • Until the two objects reach the same temperature • They will then be in Thermal Equilibrium • This is how a thermometer works Cold milk Light Hot black coffee brown coffee

Thermometers • A temperature scale is constructed by taking two fixed, reproducible temperatures • The upper fixed point is the boiling point of pure water at atmospheric pressure • The lower fixed point is the melting point of pure ice at atmospheric pressure • These were then given the values of 100 o. C and 0 o. C respectively, and the scale between them was divided by 100 to give individual degrees

Temperature - Microscopic ▪ At a microscopic level, temperature is regarded as a measure of the average kinetic energy per molecule (associated with its movement in the substance) Internal Energy ▪ Is the total potential and kinetic energy of the molecules in a substance. • Potential energy is associated with intermolecular forces. (arises from the bonds between molecules) • Kinetic energy includes both translational and rotational motion. Heat • Heat represents energy transfer due to a temperature difference • Occurs from higher to lower temperature regions

Methods of Heat Transfer • Heat can be transferred from one body to another by – Conduction (Heat transfer through material) – Convection (Heat transfer by movement of hot material) Convection ( – Radiation (Heat transfer by light) Radiation (

Conduction of heat • Conduction in solids – Heat energy causes atoms to vibrate, a vibrating atom passes this vibration to the next • Conduction in metal – Heat energy causes electrons to gain energy, electrons travel through metal (conduction) and carry heat energy with them • Metals are good conductors of both heat and electricity • The atoms at the bottom are at a higher temperature and will oscillating more strongly than those at the top.

Convection of heat • “Hot air rises” (and takes its heat with it!) – Radiators • “Hot air rises” (and takes its heat with it!) – Cumulus clouds

Convection of heat Alternating Land Sea Breezes Hurricanes Plate tectonics

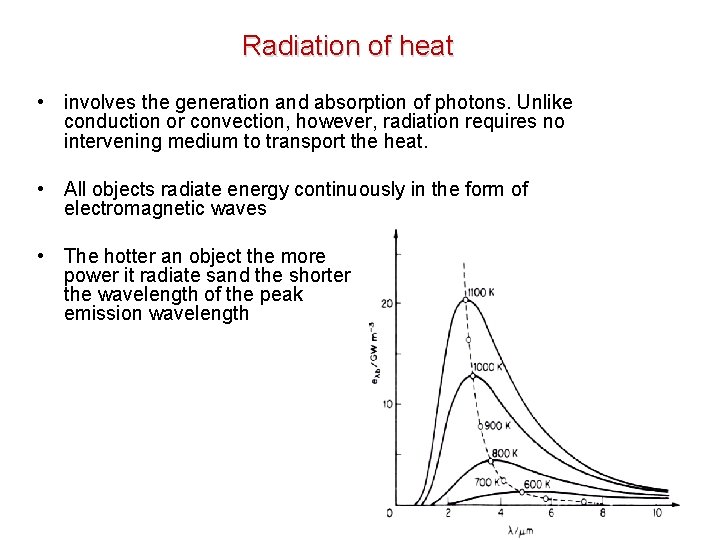
Radiation of heat • involves the generation and absorption of photons. Unlike conduction or convection, however, radiation requires no intervening medium to transport the heat. • All objects radiate energy continuously in the form of electromagnetic waves • The hotter an object the more power it radiate sand the shorter the wavelength of the peak emission wavelength

Are heat emitter also good absorbers? • Black and dull on the surface – Best emitter/absorber – Charcoal – Blackbody radiators • perfect absorber & emitter • White and polished/shiny – Good Reflectors – Stay cool in the summer

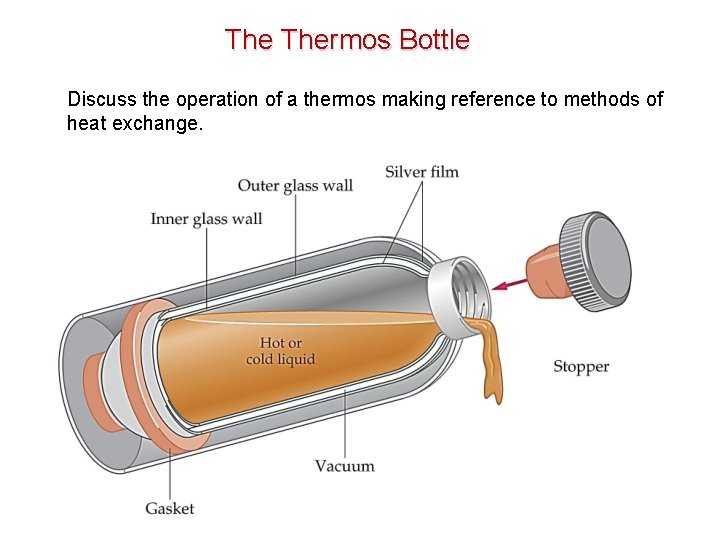
The Thermos Bottle Discuss the operation of a thermos making reference to methods of heat exchange.

The “colour” of heat • Peak wavelength of light emitted depends on temperature • Spectrum includes all wavelength longer than the peak but not many above – 20°C - peak in infrared (need thermal imaging camera to see body heat) – 800°C - peak in red (electric coil, fire glows reds) – 3000° - peak in blue (but includes green and red light hence appears white) – 2. 7 K peak in micro-wave (background emission in the universe left over from the Big Bang)

Thermal Physics Topic 3. 2 Thermal Properties of Matter

Heat Capacity/Thermal Capacity, C • A body with a high heat capacity will take in thermal energy at a slower rate than a substance with a low heat capacity because it needs more time to absorb a greater quantity of thermal energy • They also cool more slowly because they give out thermal energy at a slower rate

Specific Heat Capacity, c

• Unit masses of different substances contain – – – different numbers of molecules of different types of different masses • If the same amount of internal energy is added to each unit mass – it is distributed amongst the molecules • The average energy change of each molecule will be different for each substance • Therefore the temperature changes will be different • So the specific heat capacities will be different

Heat Capacity Whereas ‘specific’ heat capacity is ‘per kg’ of a material, heat capacity (or thermal capacity) is the energy required to raise a certain objects temperature by one Kelvin, irrespective of its mass. Heat capacity = mass x specific heat capacity C = mc m = mass (kg) C = heat capacity (JK-1) c = specific heat capacity(Jkg-1 K-1) ∆T = Change in temp (K) ∆Q = Amount of heat energy (J) Amount of energy needed to raise temperature of an object by ∆T K is ∆Q = C∆T Amount of energy needed to raise temperature of 1 kg of a substance by ∆T K is ∆Q = cm∆T The same amount is released if the temperature decreases

● Zeroth law of thermodynamics – If two thermodynamic systems are each in thermal equilibrium with a third, then they are in thermal equilibrium with each other. ● First law of thermodynamics – Energy can neither be created nor destroyed. It can only change forms. In any process, the total energy of the universe remains the same. For a thermodynamic cycle the net heat supplied to the system equals the net work done by the system. Sir James Joule 1 st law of thermodynamics: heat and work are both forms of energy Stirring water made it warm Change in temperature proportional to work done Showing equivalence of heat and mechanical energy Also that electrical current flow through a resistor causes heating Applying all these to problems:

PROBLEMS: 1. A 2. 00 -kg metal object requires 5. 02 x 103 J of heat to raise its temperature from 20. 0 °C to 40. 0 °C. What is the specific heat capacity of the metal? 126 J/(kg • C°) 2. A 0. 20 -kg lead shot is heated to 90. 0 °C and dropped into an ideal calorimeter containing 0. 50 kg of water initially at 20. 0 °C. What is the final equilibrium temperature of the lead shot? The specific heat capacity of lead is 128 J/(kg • C°); and the specific heat of water is 4186 J/(kg • C°). 20. 8 °C 3. Given that the specific heat capacity of water is 11 times that of copper, calculate the mass of copper at a temperature of 100 °C required to raise the temperature of 200 g of water from 20. 0 °C to 24. 0 °C, assuming no energy is lost to the surroundings.

4. Three litres of water at 100 °C are added to 15 litres of water at 40 °C. Calculate the temperature of the mixture. Take the mass of 1 litre of water to be 1 kg and the specific heat capacity of water to be 4. 2 × 103 J kg -1 K -1 5. A heater of 800 W is use to heat a 600 g cast iron cooker plate. How long will it take to raise the temperature of the plate by 200 o. C? Specific heat capacity of iron = 500 J/(kg K) Pt = m c T or V I t = m c T 75 s = 1 minute 15 s

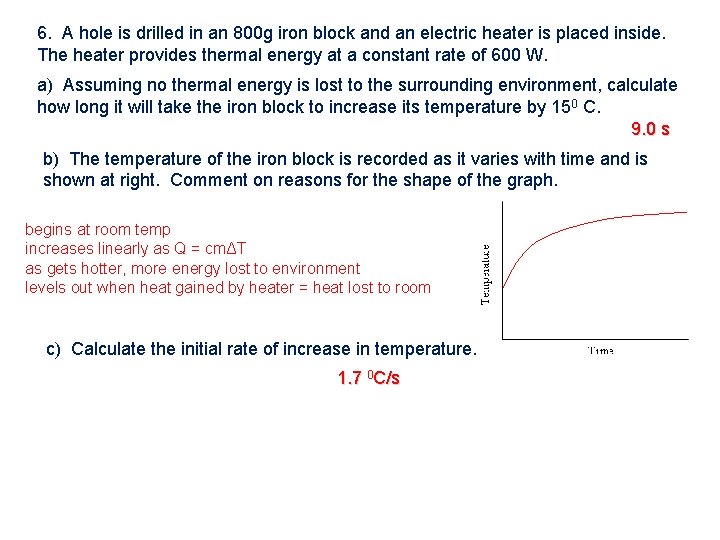
6. A hole is drilled in an 800 g iron block and an electric heater is placed inside. The heater provides thermal energy at a constant rate of 600 W. a) Assuming no thermal energy is lost to the surrounding environment, calculate how long it will take the iron block to increase its temperature by 150 C. 9. 0 s b) The temperature of the iron block is recorded as it varies with time and is shown at right. Comment on reasons for the shape of the graph. begins at room temp increases linearly as Q = cmΔT as gets hotter, more energy lost to environment levels out when heat gained by heater = heat lost to room c) Calculate the initial rate of increase in temperature. 1. 7 0 C/s

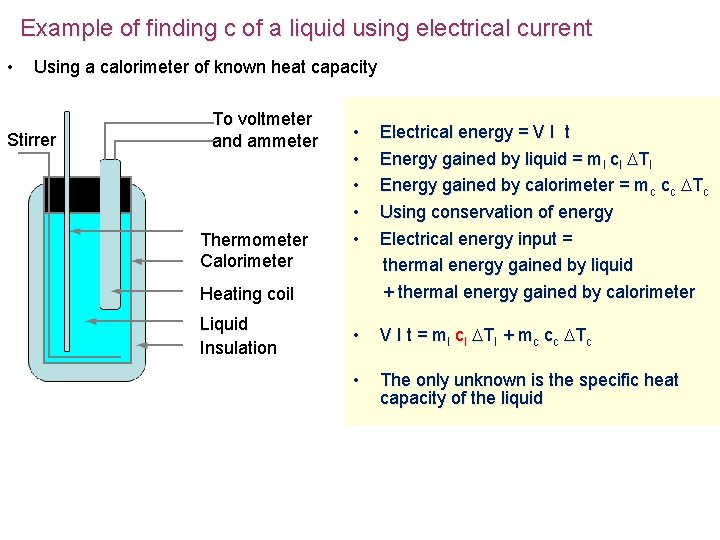
Example of finding c of a liquid using electrical current • Using a calorimeter of known heat capacity Stirrer To voltmeter and ammeter Thermometer Calorimeter Heating coil Liquid Insulation • Electrical energy = V I t • Energy gained by liquid = ml cl Tl • Energy gained by calorimeter = mc cc Tc • Using conservation of energy • Electrical energy input = thermal energy gained by liquid + thermal energy gained by calorimeter • V I t = ml cl Tl + mc cc Tc • The only unknown is the specific heat capacity of the liquid

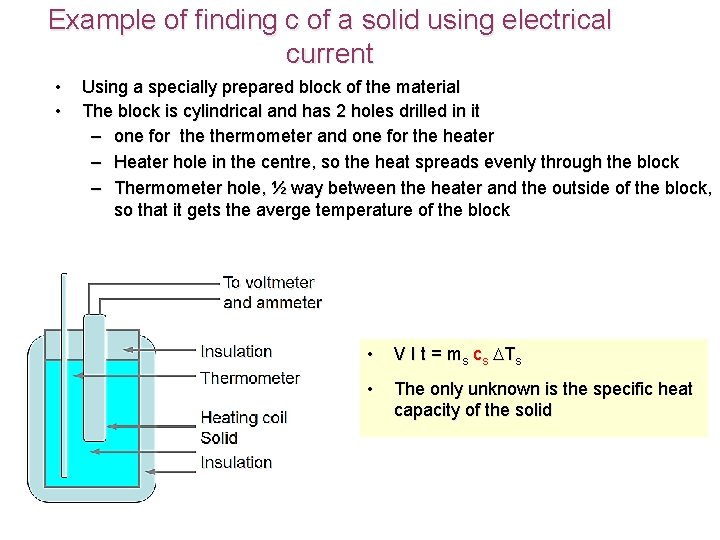
Example of finding c of a solid using electrical current • • Using a specially prepared block of the material The block is cylindrical and has 2 holes drilled in it – one for thermometer and one for the heater – Heater hole in the centre, so the heat spreads evenly through the block – Thermometer hole, ½ way between the heater and the outside of the block, so that it gets the averge temperature of the block • V I t = ms cs Ts • The only unknown is the specific heat capacity of the solid

Method of mixtures • Sometimes called the method of mixtures • In the case of solid, a known mass of solid is heated to a known temperature (usually by immersing in boiling water for a period of time) • Then it is transferred to a known mass of liquid in a calorimeter of known mass • The change in temperature is recorded and from this the specific heat capacity of the solid can be found • Energy lost by block = Energy gained by liquid and calorimeter • mb cb Tb = mw cw Tw + mc cc Tc – the SHC of water and the calorimeter are needed

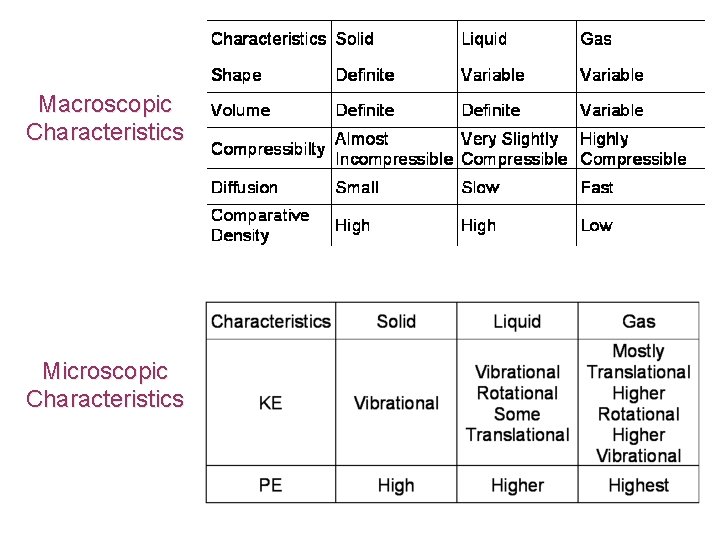
Phases (States) of Matter • • • Matter is defined as anything that has mass and occupies space There are 4 states of matter Solids, Liquids, Gases and Plasmas Most of the matter on the Earth in the form of the first 3 Most of the matter in the Universe is in the plasma state Macroscopic properties • Macroscopic properties are all the observable behaviours of that material such as shape, volume, compressibility • The many macroscopic or physical properties of a substance can provide evidence for the nature of that substance

Macroscopic Characteristics Microscopic Characteristics

Fluids • • Liquids Gases are both fluids Because they FLOW

Arrangement of Particles • Solids • Closely packed • Strongly bonded to neighbours • held rigidly in a fixed position • the force of attraction between particles gives them PE • Liquids • Still closely packed • Bonding is still quite strong • Not held rigidly in a fixed position and bonds can break and reform • PE of the particles is higher than a solid because the distance between the particles is higher • Gases • Widely spaced • Only interact significantly on closest approach or collision • Have a much higher PE than liquids because the particles are furthest apart

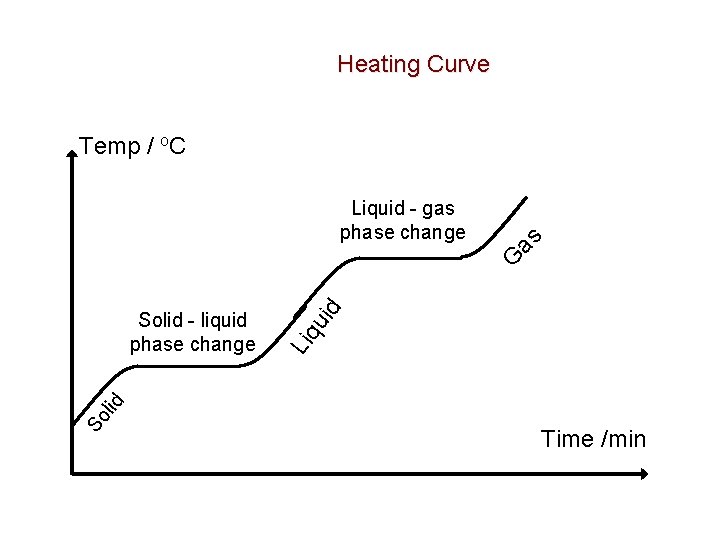
Changes of State • A substance can undergo changes of state or phase changes at different temperatures • Pure substances have definite melting and boiling points which are characteristic of the substance – When the solid is heated the particles of the solid vibrate at an increasing rate as the temperature is increased – The vibrational KE of the particles increases – At the melting point a temperature is reached at which the particles vibrate with sufficient thermal energy to break from their fixed positions and begin to slip over each other – As the solid continues to melt more and more particles gain sufficient energy to overcome the forces between the particles and over time all the solid particles are changed to a liquid – The PE of the system increases as the particles move apart – (actually it absolutely decreases towards zero) – As the heating continues the temperature of the liquid rises due to an increase in the vibrational, rotational and translational energy of the particles – At the boiling point a temperature is reached at which the particles gain sufficient energy to overcome the inter-particle forces and escape into the gaseous state. PE increases. – Continued heating at the boiling point provides the energy for all the particles to change

Heating Curve Temp / o. C Liquid - gas phase change as So Liq lid Solid - liquid phase change uid G Time /min

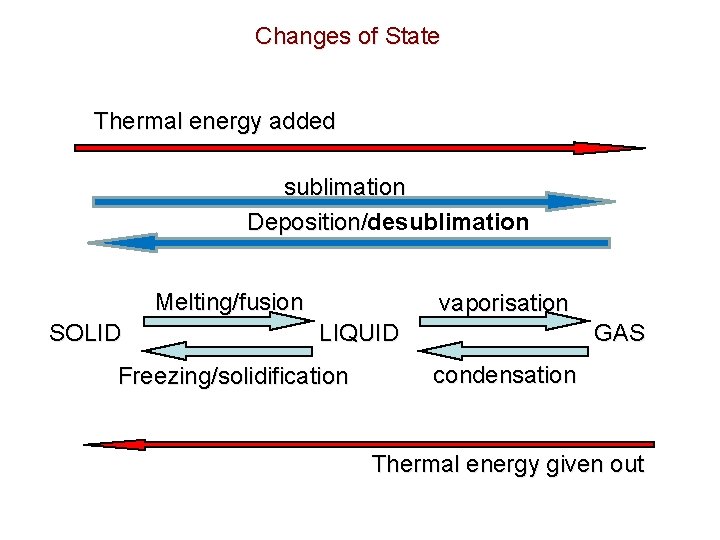
Changes of State Thermal energy added sublimation Deposition/desublimation Deposition/ Melting/fusion SOLID vaporisation LIQUID Freezing/solidification GAS condensation Thermal energy given out

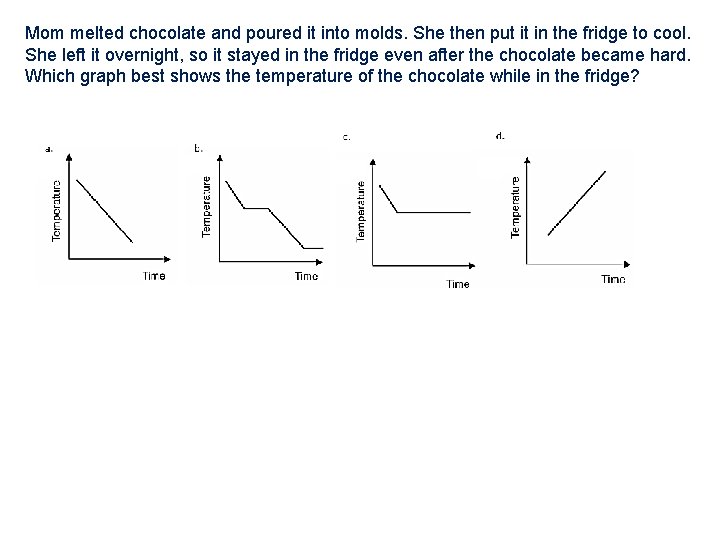
Mom melted chocolate and poured it into molds. She then put it in the fridge to cool. She left it overnight, so it stayed in the fridge even after the chocolate became hard. Which graph best shows the temperature of the chocolate while in the fridge?

Latent Heat • The thermal energy absorbed or released in phase change is called Latent Heat because it does not produce a change in temperature There is no temperature change during a phase change, thus there is no change in the kinetic energy of the particles in the material. The energy released/absorbed comes from the potential energy stored in the bonds between the particles. • Thermal energy absorbed by a body results in decrease of PE of the particles as they move closer together • Thermal energy released by a body, increases PE of the particles as they move further apart

Latent heat is thermal energy absorbed or released by a body during a change of phase (at constant pressure). L = Qat const. P unit: J Specific latent heat is thermal energy required to change the phase of 1 kg of a substance (at constant pressure). Types of Latent Heat • • • Fusion Vaporisation Sublimation • The latent heat of fusion of a substance is less than the latent heat of vaporisation or the latent heat of sublimation

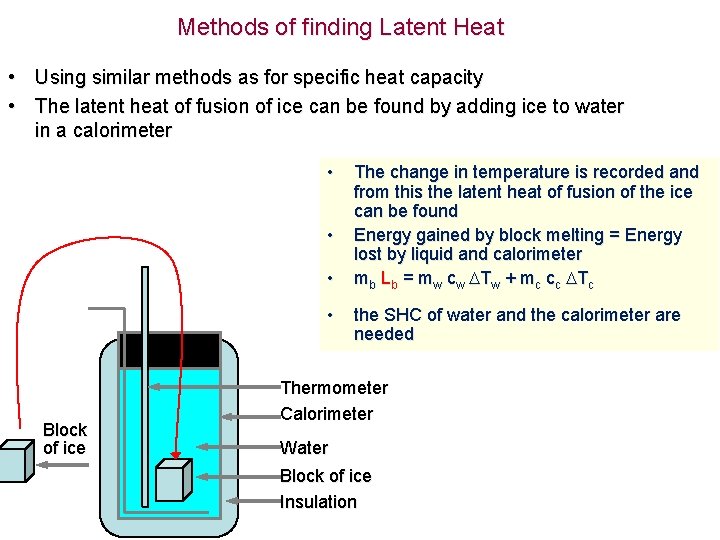
Methods of finding Latent Heat • Using similar methods as for specific heat capacity • The latent heat of fusion of ice can be found by adding ice to water in a calorimeter • • Block of ice The change in temperature is recorded and from this the latent heat of fusion of the ice can be found Energy gained by block melting = Energy lost by liquid and calorimeter mb Lb = mw cw Tw + mc cc Tc the SHC of water and the calorimeter are needed Thermometer Calorimeter Water Block of ice Insulation

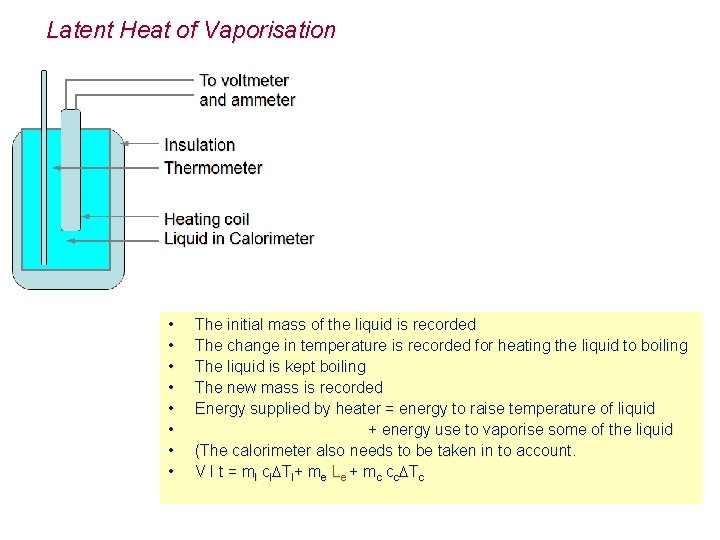
Latent Heat of Vaporisation • • The initial mass of the liquid is recorded The change in temperature is recorded for heating the liquid to boiling The liquid is kept boiling The new mass is recorded Energy supplied by heater = energy to raise temperature of liquid + energy use to vaporise some of the liquid (The calorimeter also needs to be taken in to account. V I t = ml cl Tl+ me Le + mc cc Tc

Scattered thoughts … • Under extreme conditions of heat and exercise, an individual may sweat more than a liter of liquid per hour. • The interior of roasted meat can never reach temperatures higher than the boiling point of water until all the water is cooked out of it, at which point it would resemble shoe leather. The outside is quickly dried out, however, and can reach the temperature of the surrounding cooking medium. • Cocoa butter is unique among the fats in that it is very regular in composition; whereas most other fats are actually mixtures. This gives it a very definite point; unlike butter, which softens gradually. As it melts in your mouth, it absorbs latent heat. This makes chocolate bars taste "cool". Cocoa butter is remarkably uniform in composition and structure: only three fatty acids in the majority of its triglycerides, with the same one occupying the middle position. Pure cocoa butter is quite brittle up to about 34 ℃ (93 ℉), at which point it melts quite quickly.

Changes in size: An increase in temperature generally causes bodies to expand, while a reduction in temperature causes bodies to contract. Engineers must take expansion into account when they are designing various structures (bridges, …). When concrete roads are laid down, gaps (normally filled with tar) are left between sections in order to allow for expansion. Why do solids expand with increasing temperature? The atoms or molecules in a solid vibrate at all temperatures above the absolute zero. As the temperature increases, the vibrations increase in amplitude, and this pushes the atoms further apart. This occurs in all three dimensions.

Why do liquids expand with increasing temperature? As the temperature increases, the kinetic energy of the molecules of the liquid increases. The movement of the molecules gradually overcomes forces of attraction between the molecules, with the result that they have greater freedom to move, over greater volumes. Thus the liquid expands. Water behaves in an anomalous manner. It contracts as the temperature increases from 0 ºC to 4 ºC, reaching its highest density at that temperature. This has enormous significance for aquatic life in regions with severe winters. The abnormal behaviour of water: At 4 ºC, water has its highest density. It actually contracts as the temperature rises from 0 ºC to 4ºC. This means that in regions with severe winters, lakes cool at the surface, and when the surface water reaches 4 ºC, that water, being more dense, sinks. A temperature gradient is set up, and when the water freezes, it does so at the surface. Eventually, the ice, which floats on water, acts as an insulator, protecting the water below it from further cooling. This results in lakes freezing from the top down, and not from the bottom up. This means that fishes can survive below the ice even if the air temperature is far below 0 ºC for prolonged periods. The reason for this anomalous behaviour of water is beyond the scope of the IB Physics curriculum.

Q. Explain why supply of latent heat causes a change in potential energy but not kinetic energy. A. Kelvin temperature is proportional to the KE of the molecules. Thus if the temperature hasn’t increased then the KE has also not increased. Work has been done against forces, changing the position of the molecules. Thus the PE of the molecules must change. EXAMPLE: Let: i. Specific latent heat of vaporisation (Lv) - from liquid to vapour ii. Specific latent heat of fusion (Lf) - from solid to liquid Then if 0. 5 kg of ice at 0°C is heated… i. … until it has all melted to water at 0°C ii. … until it reaches it’s boiling point at 100°C iii. … until it has vaporised to steam at 100°C Calculate the heat supplied at each stage and in total. ∆Q = m. Lv ∆Q = m. Lf ∆Q = Amount of heat energy (J) L = Specific latent heat (Jkg-1) m = mass (kg)

A i. ΔQ = m. Lf = 0. 5 x 334 x 103 = 1. 67 x 105 J ii. ΔQ = mcΔT = 0. 5 x 4200 x 100 = 2. 10 x 105 J iii. ΔQ = m. Lv = 0. 5 x 2258 x 103 = 1. 13 x 106 J Total = 1. 51 x 106 J ( = 1. 51 MJ)

Example: Which one of the following statements is UNTRUE? 1. Impurities generally decrease the melting point of substances. 2. Water can boil at room temperature. 3. Ice does not evaporate. 4. Steam may attain temperatures above 100 ºC. 5. The melting point of ice decreases with increasing pressure. 3. is correct. A great many solids, including ice, can evaporate without having first to turn into a liquid. This process is called SUBLIMATION.

Example: An iceberg has a mass of 10 000 tons. How much heat will be required to melt the iceberg (initially at 0 ºC) and bring the resulting water to a temperature of 6 ºC? (Take the specific heat capacity of water as 4. 2 k. J. kg-1. ºC-1 and the specific latent heat of fusion of ice as 334 k. J. kg-1. ) Heat required = Heat to melt the iceberg + heat to raise the water temperature Heat required to melt the iceberg = mass of iceberg x latent heat of fusion of ice = 10000 (tons) x 1000 (kg. ton-1) x 334 (k. J. kg-1) = 3. 34 x 109 k. J. Heat required to raise the water temperature = mass of water x specific heat capacity x temperature rise = 1. 0 x 107 (kg) x 4. 2 (k. J. kg-1. ºC-1) x 6 (ºC) = 2. 52 x 108 k. J Total heat = 3. 34 x 109 k. J + 2. 52 x 108 k. J = 3. 6 x 109 k. J = 3. 6 x 106 MJ

Example: An immersion heater supplies heat at a rate of 5 J. s-1 to an insulated vessel containing a certain liquid. The liquid was brought to its boiling point and kept boiling for 2 minutes, during which time the liquid lost 4. 0 g. What value for the specific latent heat of vaporization of the liquid can be calculated from this experiment? We assume that the heat supplied by the heater is the heat required to convert 4. 0 g of the liquid at its boiling point to the vapour state. P t= m L 5 (J. s-1) x 120 (s) = 4. 0 (g) x specific latent heat (J. g-1). The specific latent heat = 5 (J. s-1) x 120 (s)/4. 0 (g) = 150 J. g -1

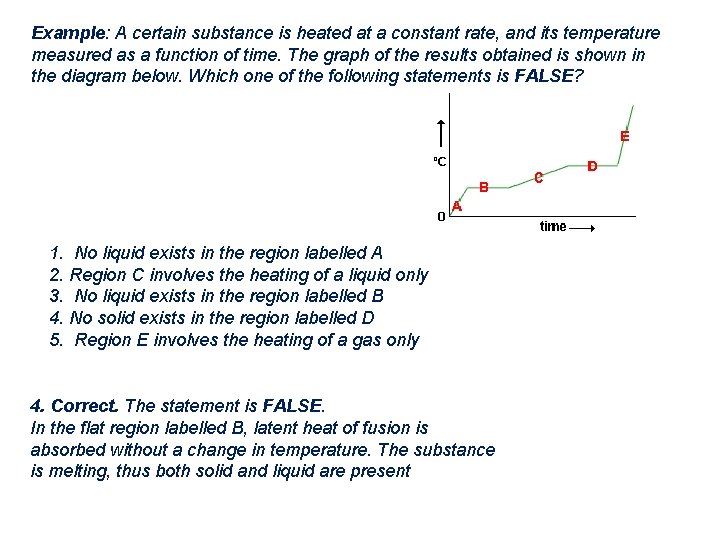
Example: A certain substance is heated at a constant rate, and its temperature measured as a function of time. The graph of the results obtained is shown in the diagram below. Which one of the following statements is FALSE? 1. No liquid exists in the region labelled A 2. Region C involves the heating of a liquid only 3. No liquid exists in the region labelled B 4. No solid exists in the region labelled D 5. Region E involves the heating of a gas only 4. Correct. The statement is FALSE. In the flat region labelled B, latent heat of fusion is absorbed without a change in temperature. The substance is melting, thus both solid and liquid are present

Example: Calculate the amount of heat required to completely convert 50 g of ice at 0 ºC to steam at 100 ºC. The specific heat capacity of water is 4. 18 k. J. kg-1. K-1. The specific latent heat of fusion of ice is 334 k. J. kg-1, and the specific heat of vaporization of water is 2260 k. J. kg-1. 5. Answer: Heat is taken up in three stages: 1. The melting of the ice, 2. the heating of the water, and 3. the vapourization of the water. The heat taken up in the complete process is the sum of the heat taken up in each stage. Heat taken up for converting ice at ºC to water at ºC mass of water x latent heat of fusion = 0. 050 (kg) x 334 (k. J. kg-1) = 16. 7 k. J Heat taken up heating the water from 0 ºC to the boiling point, 100 ºC mass of water x specific heat capacity x temperature change = 0. 05 (kg) x 4. 18 (k. J. kg-1. K-1)x 100 (º K) = 20. 9 k. J Heat taken up vapourizing the water mass of water x latent heat of vaporization = 0. 05 (kg) x 2260 k. J. kg-1 = 113 k. J The sum of these is 16. 7 + 20. 9 + 113 = 150. 6 k. J (151 k. J)



Evaporation • The process of evaporation is a change from the liquid state to the gaseous state which occurs at a temperature below the boiling point Explanation • A substance at a particular temperature has a range of particle energies • So in a liquid at any instant, a small fraction of the particles will have KE considerably greater than the average value • If these particles are near the surface of the liquid, they will have enough KE to overcome the attractive forces of the neighbouring particles and escape from the liquid as a gas • This energy is needed as gases have more PE than liquids.

Cooling • Now that the more energetic particles have escaped • The average KE of the remaining particles in the liquid will be lowered • Since temperature is related to the average KE of the particles • A lower KE infers a lower temperature Cool • This is why the temperature of the liquid falls as an evaporative cooling takes place • A substance that cools rapidly is said to be a volatile liquid • When overheating occurs in a human on hot days, the body starts to perspire • Evaporation of the perspiration cools the body

Factors Affecting The Rate • Evaporation can be increased by – Increasing temperature – (more particles have a higher KE) – Increasing surface area – (more particles closer to the surface) – Increasing air flow above the surface – (gives the particles somewhere to go to)

Topic 3. 3 Ideal Gases

The Mole • The mole is the amount of substance which contains the same number of elementary entities as there are in 12 grams of carbon-12 • Experiments show that this is 6. 02 x 1023 particles • A value denoted by NA and called the Avogadro Constant (units: mol-1) Molar Mass • Molar mass is the mass of one mole of the substance • SI units are kg mol-1 Example • Molar mass of Oxygen gas is 32 x 10 -3 kg mol-1 • How many moles and how many molecules is 20 g of Oxygen? • 20 x 10 -3 kg / 32 x 10 -3 kg mol-1 • 0. 625 mol x 6. 02 x 1023 molecules • 3. 7625 x 1023 molecules

Thermal Properties of Gases • An ideal gas can be characterized by three state variables – Pressure 1 Pa (pascal) = 1 N/1 m 2 – Volume m 3 – Temperature K • Experiments use these macroscopic properties of a gas to formulate a number of gas laws. That is historical approach. • There is another way: • The relationship between them may be deduced from kinetic theory and is called the ideal gas law:

The Ideal Gas Equation • • • PV = n. RT = Nk. T Where n is the number of moles R is the universal gas constant = 8. 31 J mol-1 K-1 N is number of molecules k is Boltzman constant = 1. 38066 x 10 -23 J/K An Ideal Gas • Is a theoretical gas that obeys the gas laws • And thus fit the ideal gas equation exactly Real Gases • Real gases conform to the gas laws under certain limited conditions • But they condense to liquids and then solidify if the temperature is lowered • Furthermore, there are relatively small forces of attraction between particles of a real gas • This is not the case for an ideal gas

The Kinetic Theory of Gases "the theory of moving molecules"; Rudolf Clausius, 1857 • The ideal gas equation is the result of experimental observations about the behavior of gases. It describes how gases behave. • A gas expands when heated at constant pressure • The pressure increases when a gas is compressed at constant temperature • But, why do gases behave this way? • What happens to gas particles when conditions such as pressure and temperature change? • That can be explained with a simple theoretical model known as the kinetic molecular theory. • The kinetic theory relates the macroscopic behaviour of an ideal gas to the microscopic behaviour of its molecules or atoms • This theory is based on the following postulates, or assumptions.

• Gases consist of tiny particles called atoms or molecules • The total number of particles in a sample is very large • The particles are in constant random motion • The range of the intermolecular forces is small compared to the average separation • The size of the particles is relatively small compared with the distance between them, so they are treated as points • Collisions of a short duration occur between particles and the walls of the container • Collisions are perfectly elastic • No forces act between the particles except when they collide • Between collisions the particles move in straight lines • And obey Newton’s Laws of motion

• Gas consists of large numbers of tiny particles called atoms or molecules that behave like hard, spherical objects in a state of constant, random motion. • The size of the particles is relatively small compared with the distance between them, so they are treated as points • Collisions of a short duration occur between particles and the walls of the container • No Intermolecular forces act between the particles except when they collide, so between collisions the particles move in straight lines • Collisions are perfectly elastic (none of the energy of a gas particle is lost in collisions) • Energy can be transferred between molecules during collisions. • They all obey Newton’s Laws of motion

Macroscopic Behaviour § The large number of particles ensures that the number of particles moving in all directions is constant at any time § With these basic assumptions we can relate the pressure of a gas (macroscopic behaviour) to the behavior of the molecules themselves (microscopic behaviour).

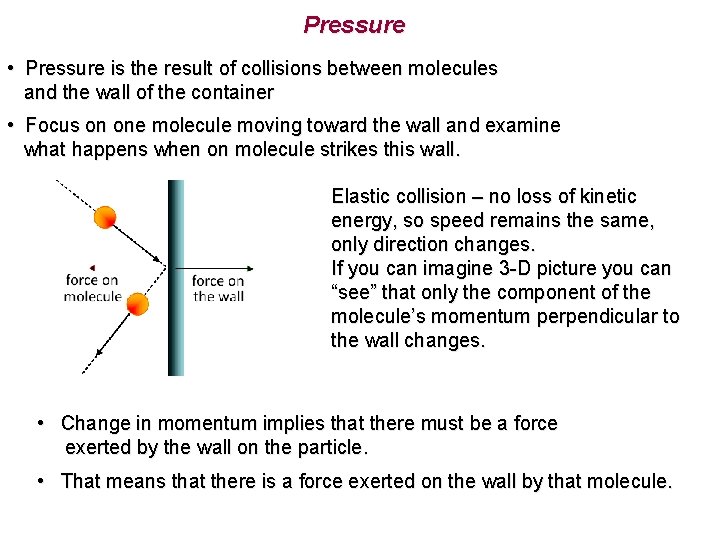
Pressure • Pressure is the result of collisions between molecules and the wall of the container • Focus on one molecule moving toward the wall and examine what happens when on molecule strikes this wall. Elastic collision – no loss of kinetic energy, so speed remains the same, only direction changes. If you can imagine 3 -D picture you can “see” that only the component of the molecule’s momentum perpendicular to the wall changes. • Change in momentum implies that there must be a force exerted by the wall on the particle. • That means that there is a force exerted on the wall by that molecule.

• The average pressure on the wall is the average of all microscopic forces per unit area: • It can be shown that the pressure on the wall can be expressed as: • Now, finally we have the pressure in a gas expressed in terms of molecular properties. • This is a surprisingly simple result! The macroscopic pressure of a gas relates directly to the average kinetic energy per molecule. • We got key connection between microscopic behaviour and macroscopic observables.

• If we compare the ideal-gas equation of state: PV = Nk. T, with the result from kinetic theory: PV = ⅓ N m (v 2)avg we find • The average translational kinetic energy of molecules in a gas is directly proportional to the absolute temperature. • The higher the temperature, according to kinetic theory, the faster the molecules are moving on the average. • At absolute zero they have zero kinetic energy. Can not go lower. • This relation is one of the triumphs of the kinetic energy theory.

Absolute Temperature • The absolute temperature is a measure of the average kinetic energy of its molecules • If two different gases are at the same temperature, their molecules have the same average kinetic energy, but more massive molecules will have lower average speed. • If the temperature of a gas is doubled, the average kinetic energy of its molecules is doubled Molecular Speed • Although the molecules of gas have an average kinetic energy (and therefore an average speed) the individual molecules move at various speeds • Some are moving fast, others relatively slowly • At higher temperatures at greater fraction of the molecules are moving at higher speeds • For O 2 molecules at 300 K, the most probable speed is 390 m/s. • When temperature increases to 1100 K the most probable speed increases to roughly 750 m/s. Other speed occur as well, from speeds near zero to those that are very large, but these have much lower probabilities.

Application of the "Kinetic Molecular Theory" to the Gas Laws Microscopic justification of the laws

Pressure Law (Gay-Lussac’s Law) Effect of a pressure increase at a constant volume Macroscopically: at constant volume the pressure of a gas is proportional to its temperature: PV = Nk. T → P = (const) T example: a closed jar, or aerosol can, thrown into a fire will explode due to increase in gas pressure inside.

Microscopically: • As T increases, KE of molecules increase • That implies greater change in momentum when they hit the wall of the container • Thus microscopic force from each molecule on the wall will be greater • As the molecules are moving faster on average they will hit the wall more often • The total force will increase, therefore the pressure will increase

The Charles’s law Effect of a volume increase at a constant pressure Macroscopically: at constant pressure, volume of a gas is proportional to its temperature: PV = Nk. T → V = (const) T

Microscopically: • An increase in temperature means an increase in the average kinetic energy of the gas molecules, thus an increase in speed • There will be more collisions per unit time, furthermore, the momentum of each collision increases (molecules strike the wall harder) • Therefore, there would be an increase in pressure • If we allow the volume to change to maintain constant pressure, the volume will increase with increasing temperature

Boyle - Marriott’s Law Effect of a pressure decrease at a constant temperature Macroscopically: at constant temperature the pressure of a gas is inversely proportional to its volume: PV = Nk. T → P = (const)/V

Microscopically: • Constant T means that the average KE of the gas molecules remains constant • This means that the average speed of the molecules, v, remains unchanged • If the average speed remains unchanged, but the volume increases, this means that there will be fewer collisions with the container walls over a given time • Therefore, the pressure will decrease
 How to write a physics ia
How to write a physics ia Difference between curie temperature and neel temperature
Difference between curie temperature and neel temperature Difference between curie temperature and neel temperature
Difference between curie temperature and neel temperature Difference between antiferromagnetism and ferrimagnetism
Difference between antiferromagnetism and ferrimagnetism What is a clincher sentence
What is a clincher sentence Narrow down the topic
Narrow down the topic Heat vs thermal energy vs temperature
Heat vs thermal energy vs temperature Heat thermal energy and temperature
Heat thermal energy and temperature Thermal energy vs heat
Thermal energy vs heat Thermal energy vs heat energy
Thermal energy vs heat energy Heat vs thermal energy vs temperature
Heat vs thermal energy vs temperature Thermal cycler temperature verification system
Thermal cycler temperature verification system Thermal energy vs temperature
Thermal energy vs temperature Thermal energy vs temperature
Thermal energy vs temperature Q mct
Q mct Section 3 using thermal energy worksheet answer key
Section 3 using thermal energy worksheet answer key Thermal transfer vs direct thermal printing
Thermal transfer vs direct thermal printing Physics heat and temperature
Physics heat and temperature Examples of convection
Examples of convection Topic 6 ib physics
Topic 6 ib physics Ib physics chapter 5
Ib physics chapter 5 Ib physics topic 3
Ib physics topic 3 Quantum and nuclear physics
Quantum and nuclear physics Quantum nuclear physics
Quantum nuclear physics Physics chapter 1 introduction and mathematical concepts
Physics chapter 1 introduction and mathematical concepts Quantum numbers khan academy
Quantum numbers khan academy Thermal energy formula
Thermal energy formula Thermal equilibrium formula
Thermal equilibrium formula Thermal physics definition
Thermal physics definition Modern physics vs classical physics
Modern physics vs classical physics University physics with modern physics fifteenth edition
University physics with modern physics fifteenth edition °c is a unit of what gas property
°c is a unit of what gas property Wine label
Wine label Which elements are liquids at room temperature
Which elements are liquids at room temperature Uniformitarianism examples
Uniformitarianism examples Usairnet temperature map
Usairnet temperature map What single factor controls humidity
What single factor controls humidity Vray sphere light
Vray sphere light Temperature
Temperature Temperature
Temperature Median temperature
Median temperature Log mean temperature difference
Log mean temperature difference Where are your pulse points
Where are your pulse points Torch lake water temperature
Torch lake water temperature Maintenance of body temperature
Maintenance of body temperature Countercurrent exchange thermoregulation
Countercurrent exchange thermoregulation Thermogenesis
Thermogenesis Body temperature maintenance
Body temperature maintenance Busbar temperature monitoring
Busbar temperature monitoring Gibbs free energy vs temperature
Gibbs free energy vs temperature Internal energy formula thermodynamics
Internal energy formula thermodynamics Heating curve of water
Heating curve of water Heat deflection temperature
Heat deflection temperature Whats thermal energy
Whats thermal energy What is the average temperature of the amazon rainforest
What is the average temperature of the amazon rainforest Taiga ecosystem food chain
Taiga ecosystem food chain What is the relationship between temperature and volume
What is the relationship between temperature and volume Jaime frade
Jaime frade Venus temperature profile
Venus temperature profile Innercore temperature
Innercore temperature Boyle's law variables
Boyle's law variables Desert biome
Desert biome Avogadro's law relationship
Avogadro's law relationship Tundra
Tundra Life in the abyssal zone
Life in the abyssal zone Temperature is a measure of *
Temperature is a measure of * What does temperature measure
What does temperature measure Temperature is the measure of the average —
Temperature is the measure of the average — Homeotherms and heterotherms
Homeotherms and heterotherms Oral temperature range
Oral temperature range Abbreviation for temperature pulse and respiration
Abbreviation for temperature pulse and respiration Principle of measurement of temperature
Principle of measurement of temperature Heat and temperature
Heat and temperature