The Mathematics of Map Coloring The FourColor Theorem





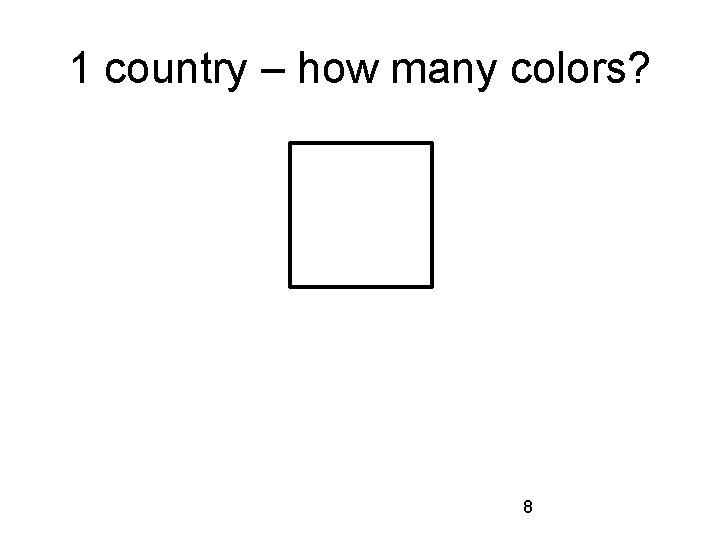








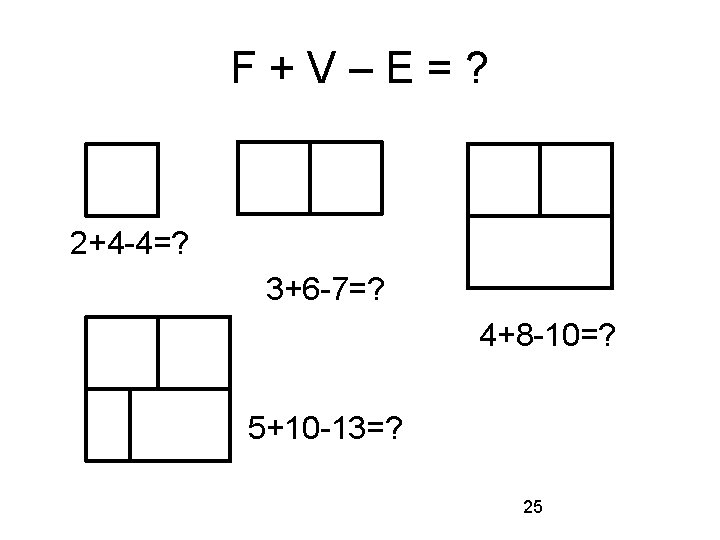

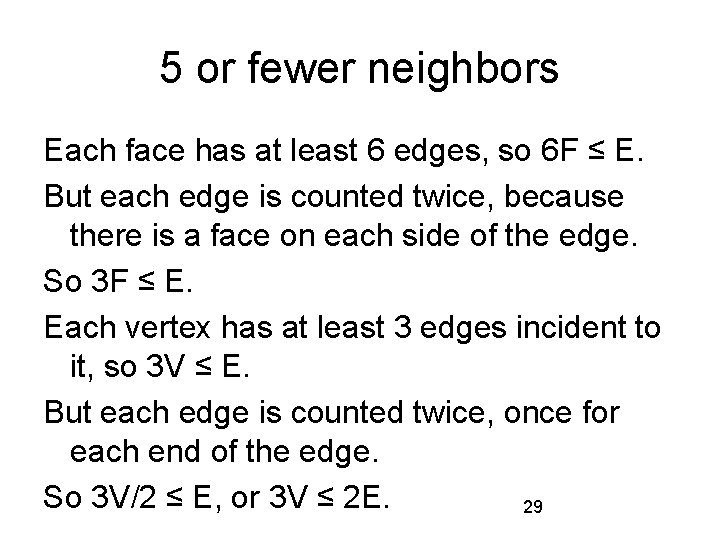
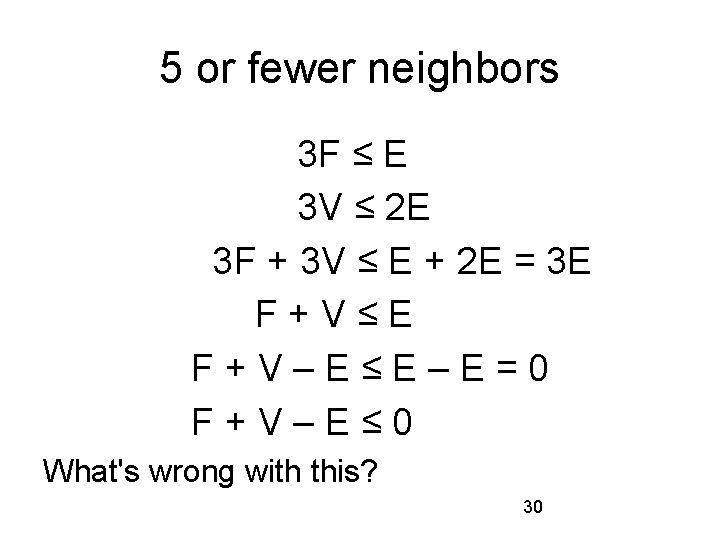
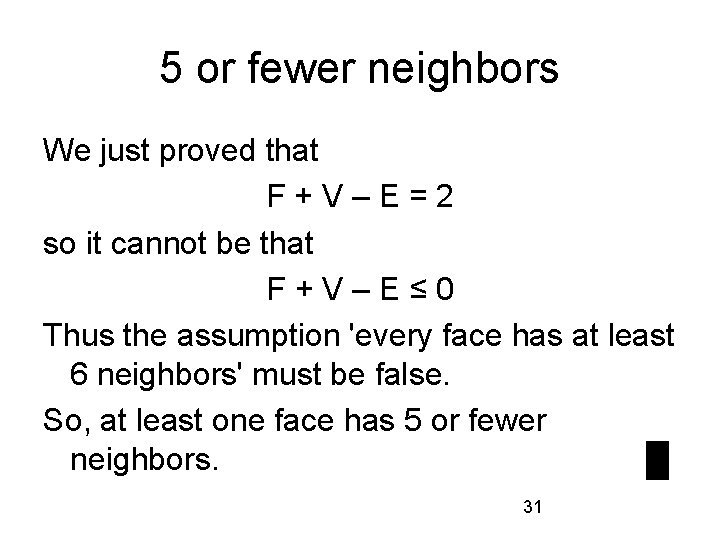























- Slides: 74

The Mathematics of Map Coloring – The Four-Color Theorem Roger House Scientific Buzz Café French Garden Sebastopol, CA 2013 Jan 17 Copyright © 2013 Roger House

The Problem You have a map of some sort, say a map of the counties of England, and you wish to color each county in such a way that no two adjacent counties are the same color. Of course, you could use a different color for each county, but there's a condition: Use as few colors as possible.

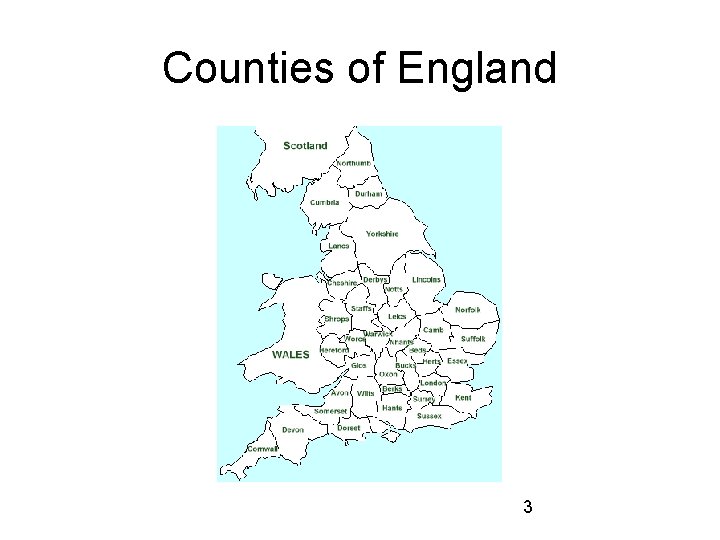
Counties of England 3

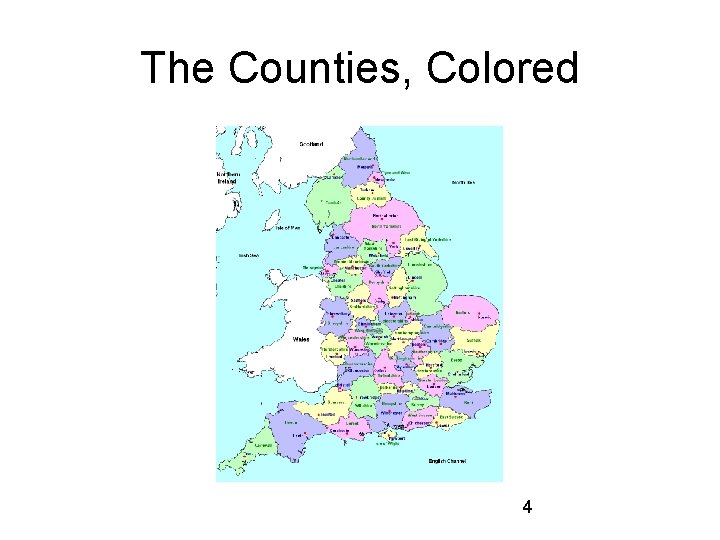
The Counties, Colored 4

Why Counties of England? Some time before 1852 October 23, Francis Guthrie (1831 -99) was coloring a map of the counties of England when several questions occurred to him: What is the minimum number of colors that would work for the counties of England? What is the minimum number of colors that would work for any map? 5

1852 October 23 How do we know Francis Guthrie came up with the problem before 1852 October 23? Because on that date his brother, Frederick Guthrie (1833 -86), sent a letter to Augustus de Morgan (1806 -71) stating the problem and crediting Francis with it. On the very same day, de Morgan sent a letter to Sir William Rowan Hamilton (1805 -65) telling him of the problem. 6

How to begin? Mathematicians present their results in tidy, logical, step-by-step, pristine papers in learned journals. They virtually never arrive at their results in the manner suggested by their papers. They start with pencil and paper (or computers) and try this and try that, and offer sacrifices to the Math Mistress. We will do the same. 7
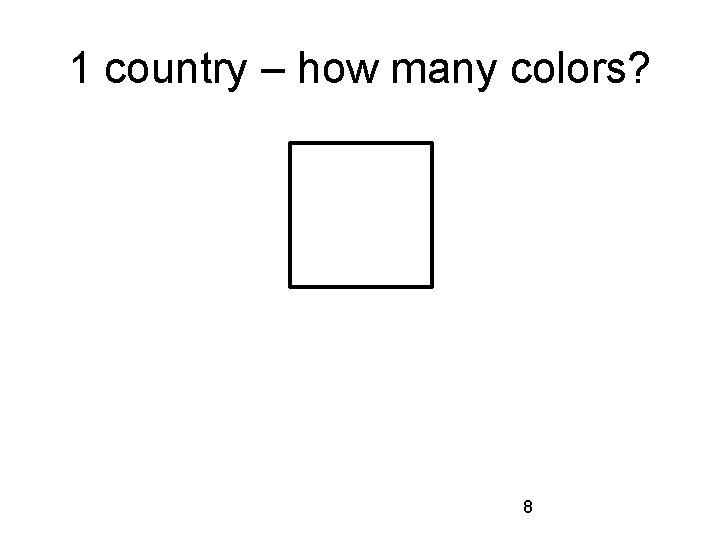
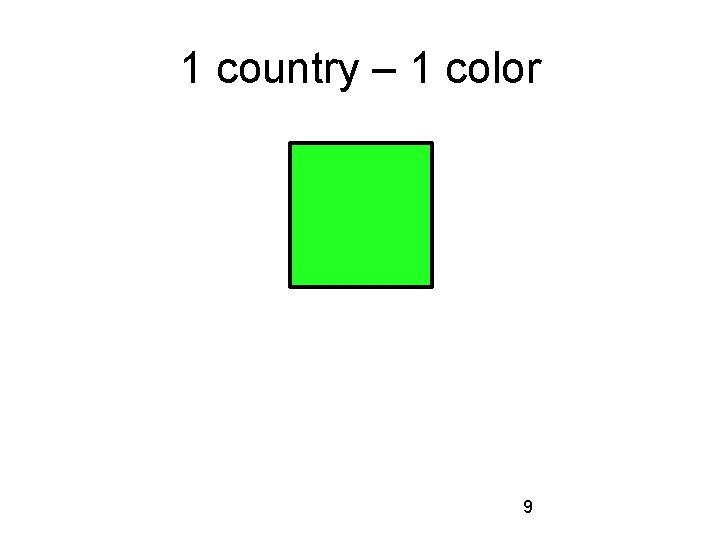
1 country – how many colors? 8

1 country – 1 color 9

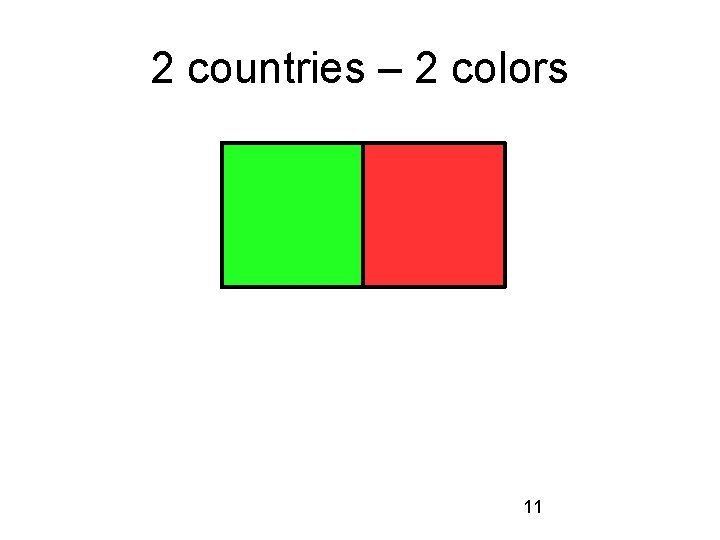
2 countries – how many colors? 10

2 countries – 2 colors 11

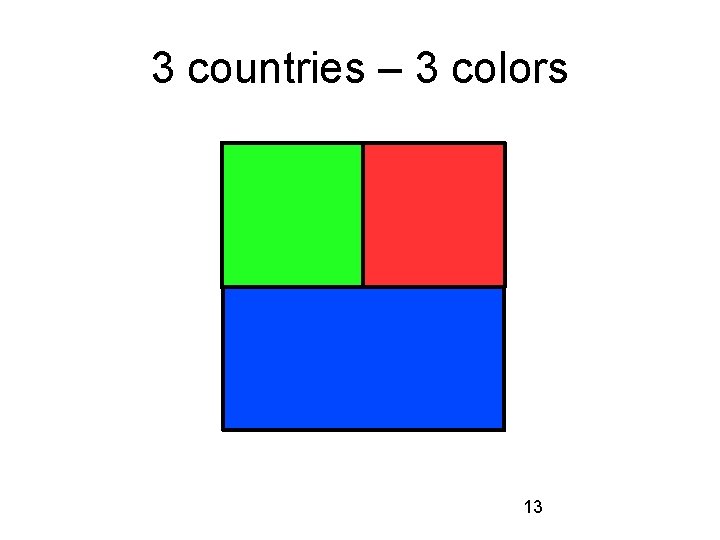
3 countries – how many colors? 12

3 countries – 3 colors 13

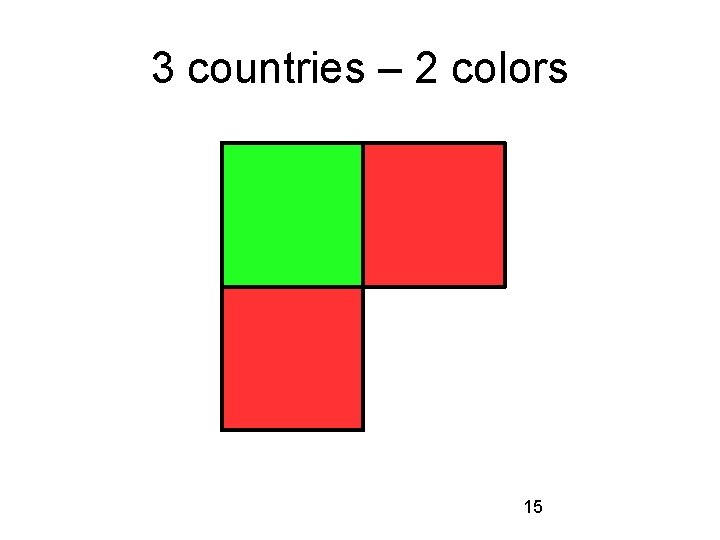
3 countries – how many colors? 14

3 countries – 2 colors 15

4 countries – how many colors? 16

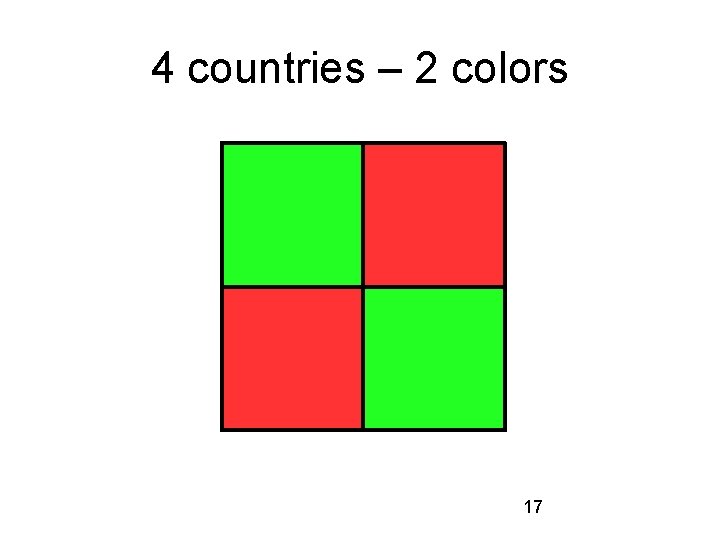
4 countries – 2 colors 17

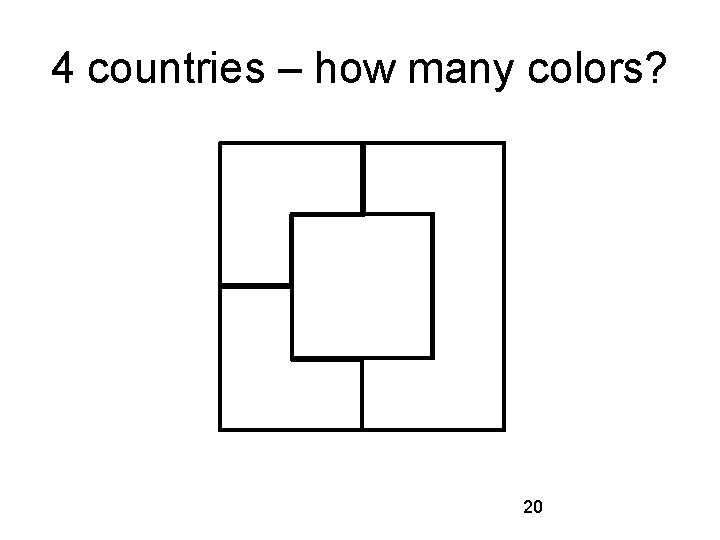
4 countries – how many colors? 18

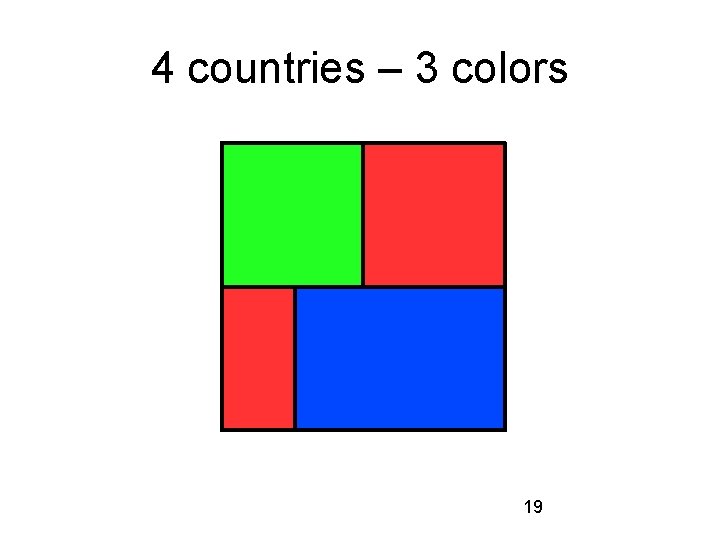
4 countries – 3 colors 19

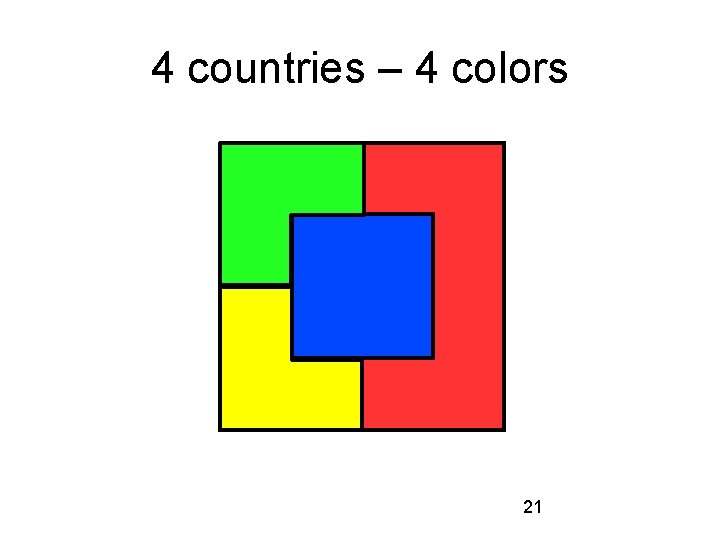
4 countries – how many colors? 20

4 countries – 4 colors 21

Important fact The previous example proves something rather important about map coloring: The minimum number of colors required to color a map so that no two adjacent countries are the same color is four. We now have a lower bound on the number we seek. Can we find an upper bound? 22

Do the math Useful facts leading to an upper bound: 1. The Euler Characteristic of a map is two. 2. Every map contains at least one country with five or fewer neighbors. 3. At most six colors are needed to color any map. Note that this last result gives us an upper bound on the number of colors needed. 23

Leonhard Euler (1707 -83) Leonhard Euler discovered just about everything: Euler angles Euler totient function Euler's formula Euler constant Eulerian path Euler-Lagrange equation Euler method Euler identity His collected works: 76 volumes, so far. . . We focus on the Euler Characteristic. 24
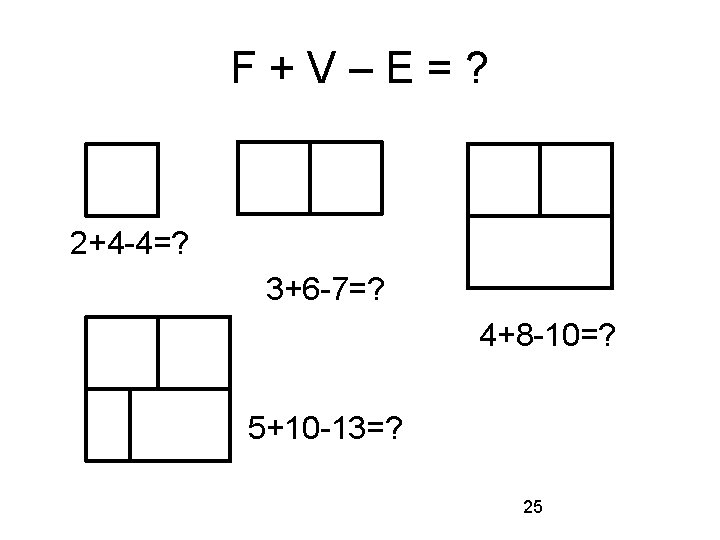
F+V–E=? 2+4 -4=? 3+6 -7=? 4+8 -10=? 5+10 -13=? 25

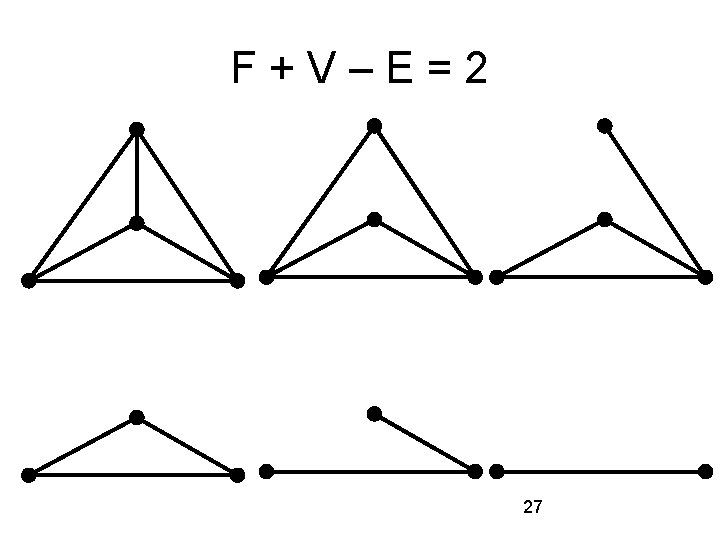
Euler Characteristic F+V-E is called the Euler Characteristic. It certainly looks like it is always 2. In fact, this is the case for maps drawn in the plane or on a sphere. We will sketch an informal proof of this. For a map drawn on a doughnut, things are different: The Euler Characteristic on a torus is zero. 26

F+V–E=2 27

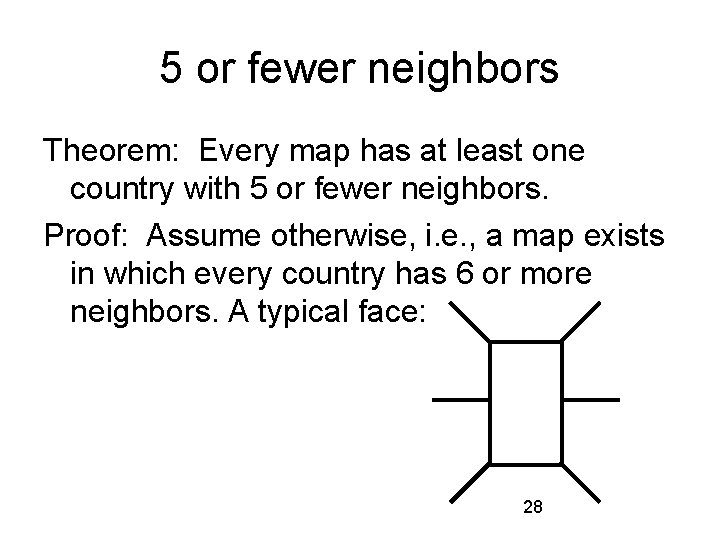
5 or fewer neighbors Theorem: Every map has at least one country with 5 or fewer neighbors. Proof: Assume otherwise, i. e. , a map exists in which every country has 6 or more neighbors. A typical face: 28
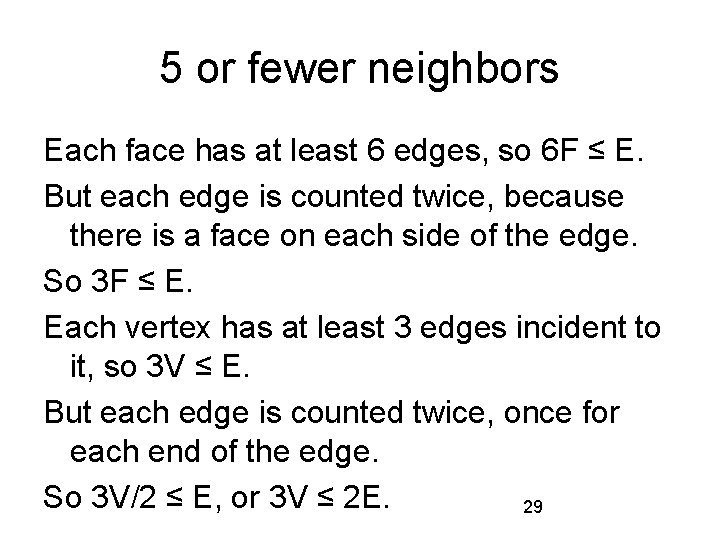
5 or fewer neighbors Each face has at least 6 edges, so 6 F ≤ E. But each edge is counted twice, because there is a face on each side of the edge. So 3 F ≤ E. Each vertex has at least 3 edges incident to it, so 3 V ≤ E. But each edge is counted twice, once for each end of the edge. So 3 V/2 ≤ E, or 3 V ≤ 2 E. 29
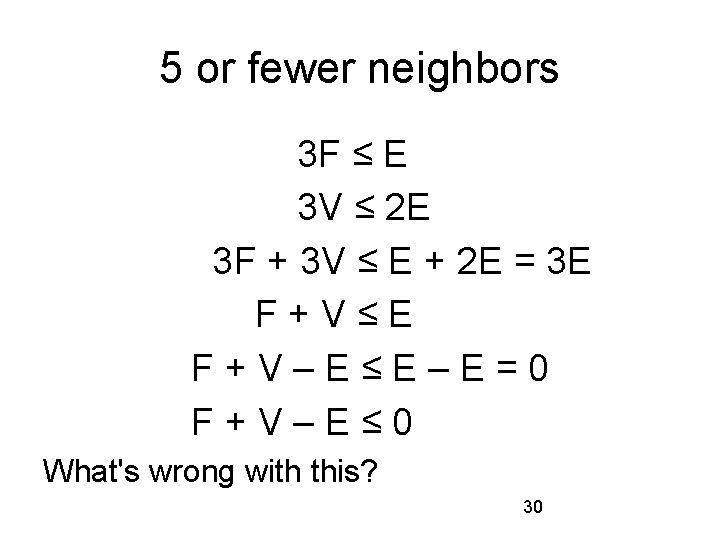
5 or fewer neighbors 3 F ≤ E 3 V ≤ 2 E 3 F + 3 V ≤ E + 2 E = 3 E F+V≤E F+V–E≤E–E=0 F+V–E≤ 0 What's wrong with this? 30
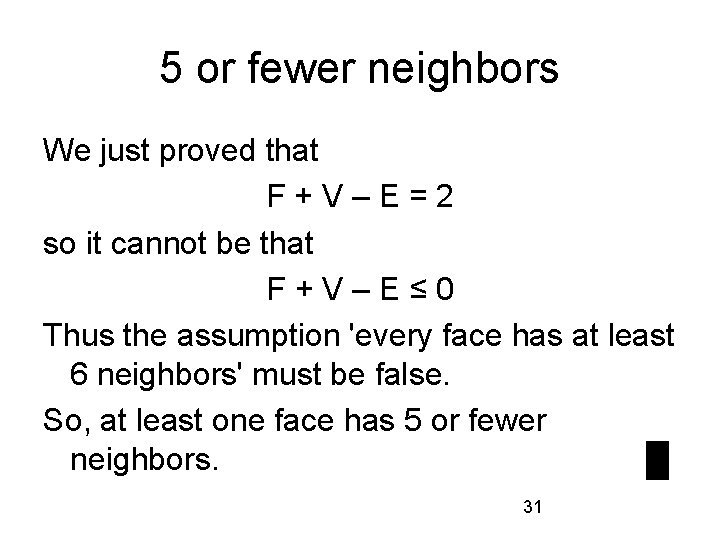
5 or fewer neighbors We just proved that F+V–E=2 so it cannot be that F+V–E≤ 0 Thus the assumption 'every face has at least 6 neighbors' must be false. So, at least one face has 5 or fewer neighbors. █ 31

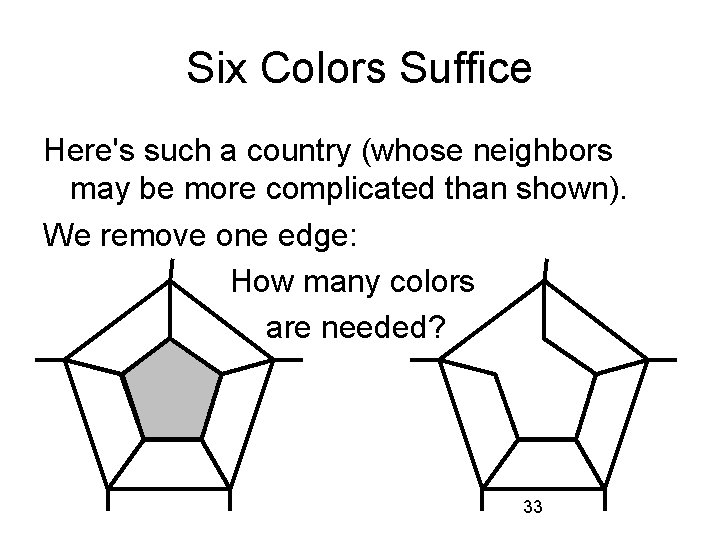
Six Colors Suffice Theorem: Every map can be colored with no more than 6 colors in such a way that no two countries sharing a common boundary have the same color. Proof: Assume otherwise, i. e. , maps exist which require more than 6 colors. From the set of such maps pick one with the fewest countries. By theorem we just proved, one country 32 has 5 or fewer neighbors.

Six Colors Suffice Here's such a country (whose neighbors may be more complicated than shown). We remove one edge: How many colors are needed? 33

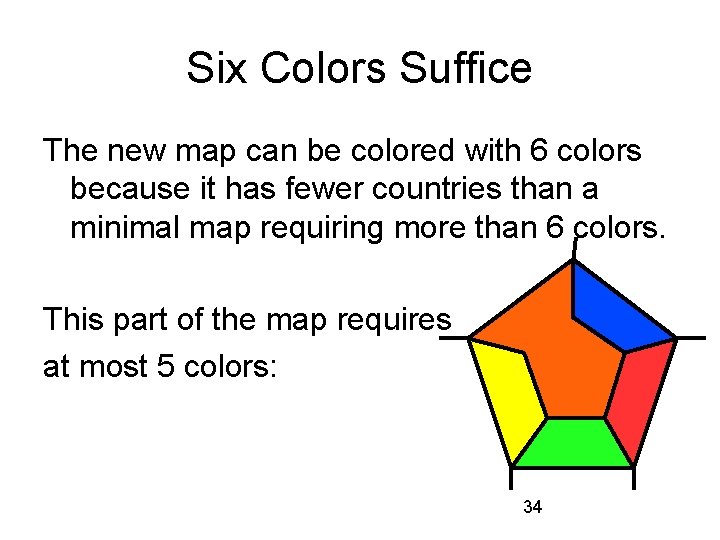
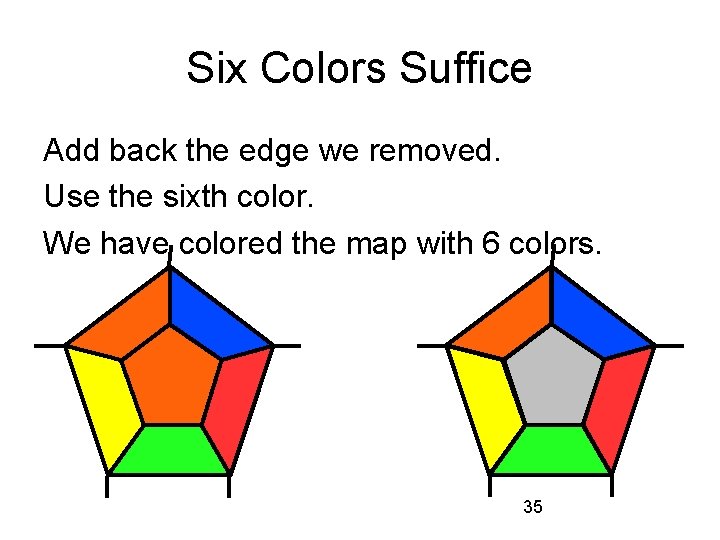
Six Colors Suffice The new map can be colored with 6 colors because it has fewer countries than a minimal map requiring more than 6 colors. This part of the map requires at most 5 colors: 34

Six Colors Suffice Add back the edge we removed. Use the sixth color. We have colored the map with 6 colors. 35

Six Colors Suffice Wait a minute! We started with a map which required more than 6 colors. But we have just shown how to color it with 6 colors. This is a contradiction. Which proves that all maps require no more than 6 colors. █ 36

Pick a number: 4, 5, or 6? So now we know that the minimum number of colors required to color any map so that no two adjacent countries have the same color is 4, 5, or 6. Well, which is it? 4? 5? or 6? It looks as if 4 is the answer, but is it? For a mathematician, this is an unsatisfactory situation. “Wir müssen wissen!” 37

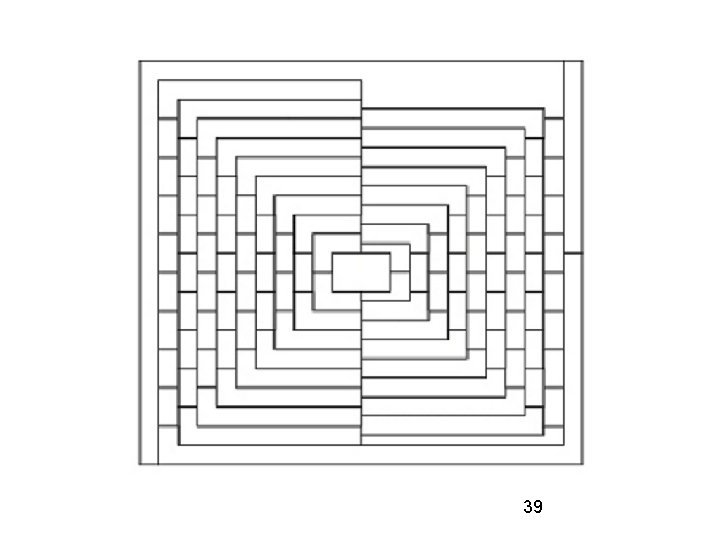
Break time While on break, you might try coloring the following map to see if it requires 4, 5, or 6 colors: 38

39

No activity for several decades Except for a couple of letters and a book review, there is no mention of the Four Color Problem from 1852 to 1878. On 1878 July 13, Arthur Cayley (1821 -95) inquired of the mathematical section of the Royal Society if a solution had been submitted. None had, but this focused attention on the problem. 40

Solved, at last In 1878 Sir Alfred Bray Kempe (1849 -1922) announced in Nature that he had found “the solution of a problem which recently achieved some renown. ” In 1879 his proof was published in the American Journal of Mathematics Pure and Applied. Problem solved: Four colors suffice. 41

How did he do it? We will give a rough idea of Kempe's approach. We won't examine a lot of picky cases which the actual proof dealt with. We'll focus on example maps, not the general case. But, you'll get the idea. . . 42

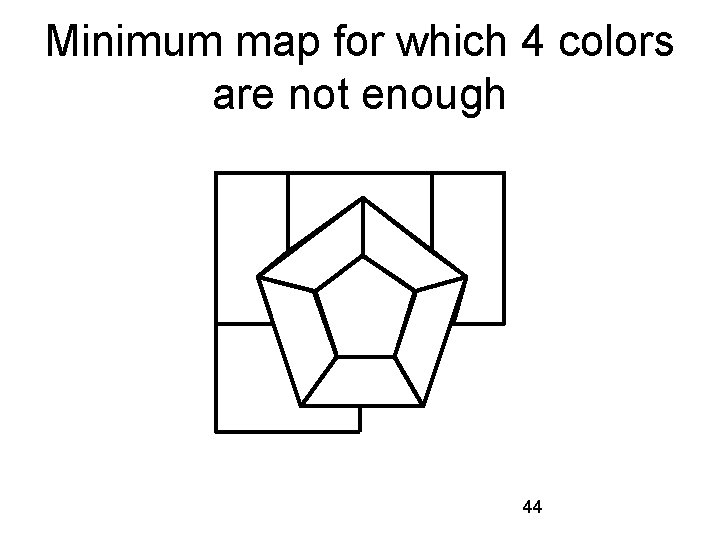
Is this approach familiar? Assume that some maps exist which require more than four colors. From these maps, pick one that has the fewest number of countries. There may be more than one such map. Never mind – pick any map from the set of those with the fewest countries. Say this map: 43

Minimum map for which 4 colors are not enough 44

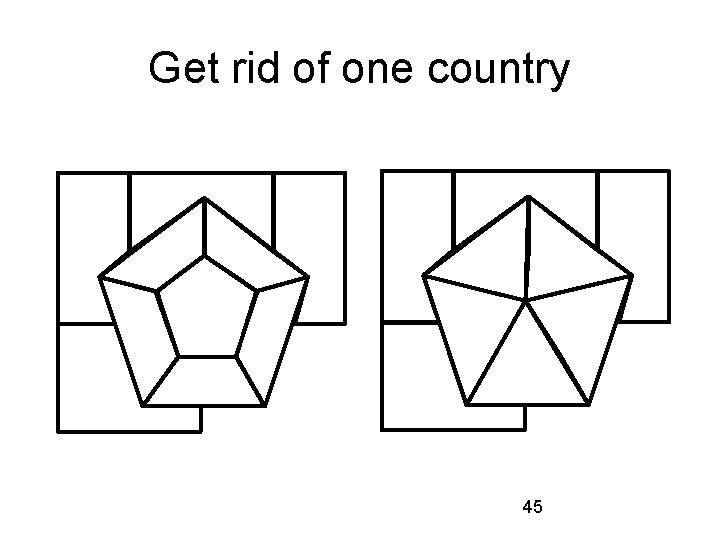
Get rid of one country 45

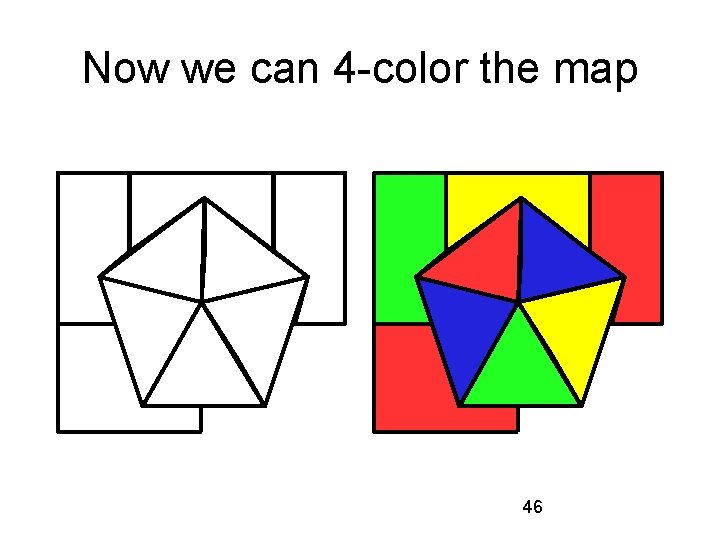
Now we can 4 -color the map 46

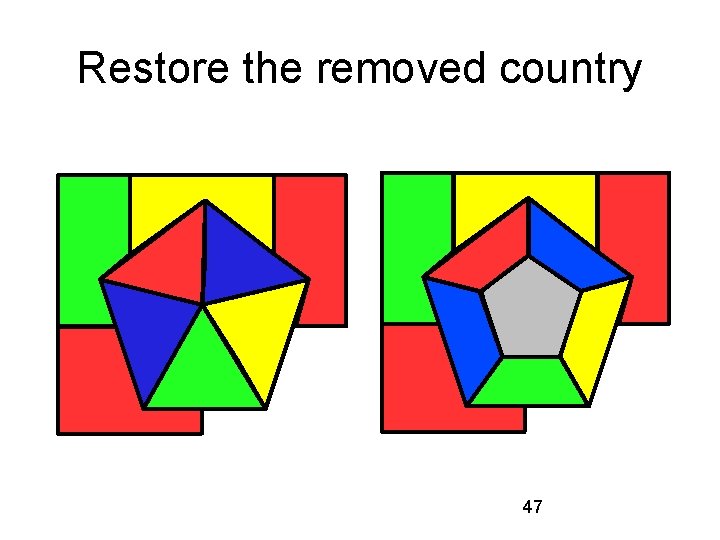
Restore the removed country 47

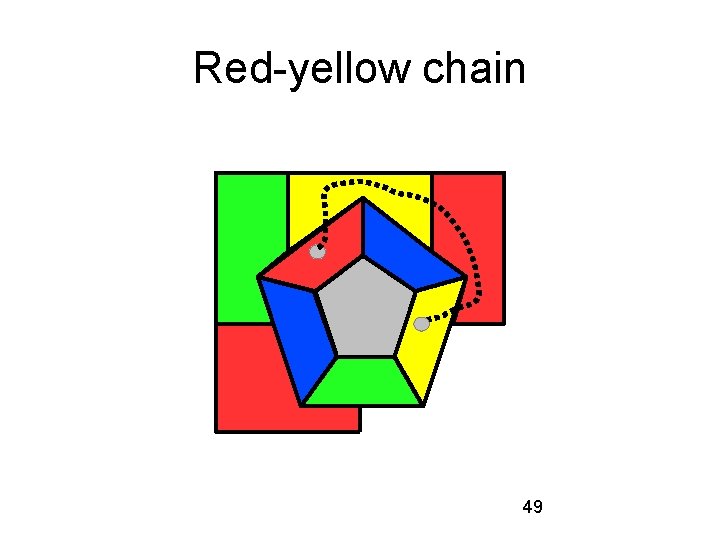
Change gray to what? We want to color the gray country red, green, blue, or yellow. In order to do this, we must change the colors of some of the countries bordering the gray country. Consider a red-yellow chain: 48

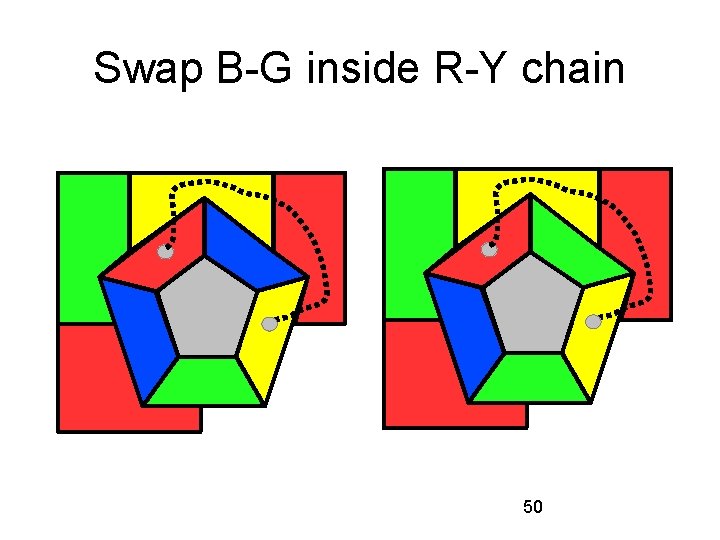
Red-yellow chain 49

Swap B-G inside R-Y chain ` 50

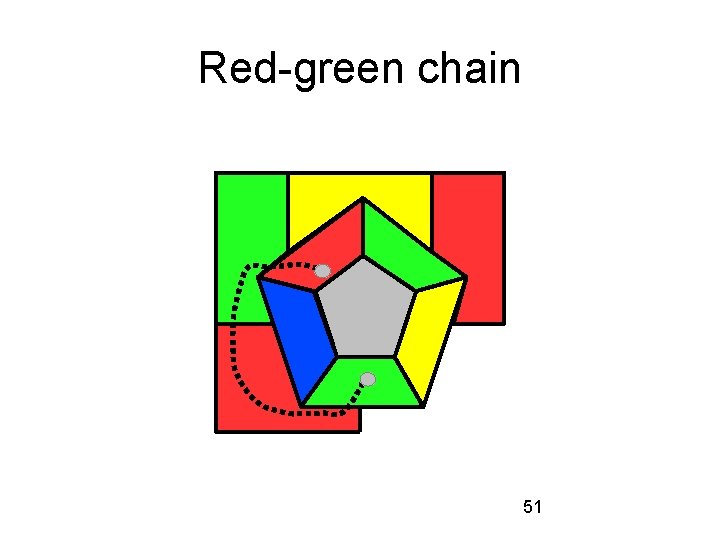
Red-green chain 51

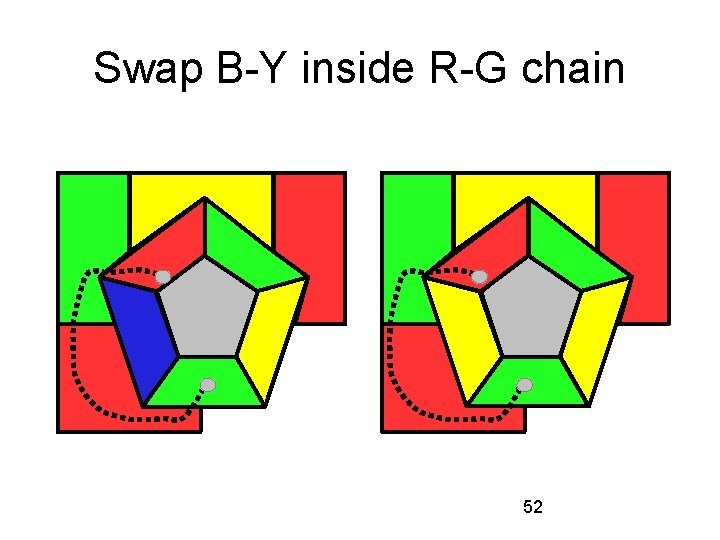
Swap B-Y inside R-G chain 52

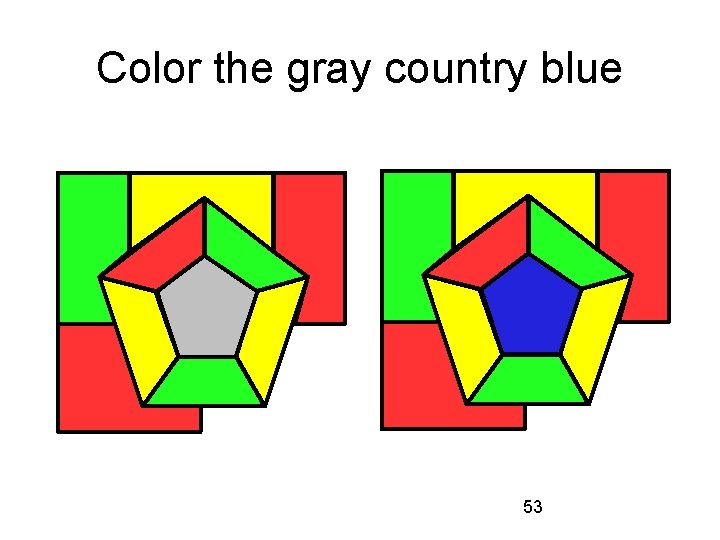
Color the gray country blue 53

Here's a 4 -coloring of the map What's wrong with this picture? 54

Four Colors Suffice! The map requires more than 4 colors. But we have just shown that it can be colored with 4 colors. Contradiction! So theorem is proved: There are no maps which need more than 4 colors. █ Ah (a sigh of relief), all is right with the world. 55

Hold it a second We haven't actually proved theorem. We've looked at one example map and showed how Kempe argued that it could be 4 -colored, using Kempe chains. His actual proof dealt with a number of cases which we've ignored. It dealt with general cases, not examples. But we've seen the main idea of his method. 56

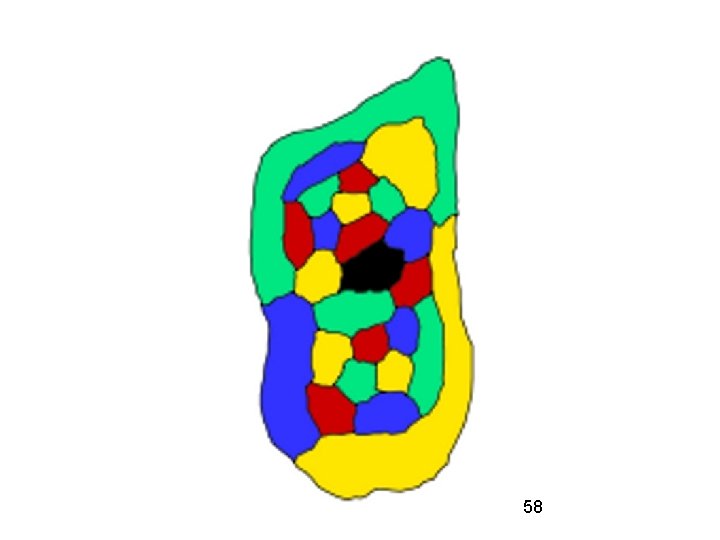
Trouble in paradise Kempe's proof settled things – after 1879 not much was heard about map coloring. Until … In 1890, eleven years after Kempe's proof came out, Percy John Heawood (18611955) published a paper entitled Mapcolour theorem. The paper contained this map: 57

58

59

60

61

62

Ouch! Heawood's example demolished Kempe's proof, i. e. , Kempe's proof had a hole in it. Kempe had not realized that applying his chains twice simultaneously could lead to an improper coloring. So, suddenly, the Four Color Theorem once again became the Four Color Conjecture. However, all is not lost. . . 63

The Five Color Theorem Heawood showed that a modification of Kempe's method resulted in a proof of the Five Color Theorem. So now we know that the minimum number of colors needed is 4 or 5. What is needed to decide if 4 colors suffice? A proof that works for all maps, i. e. , a proof that works for an infinite number of maps. 64

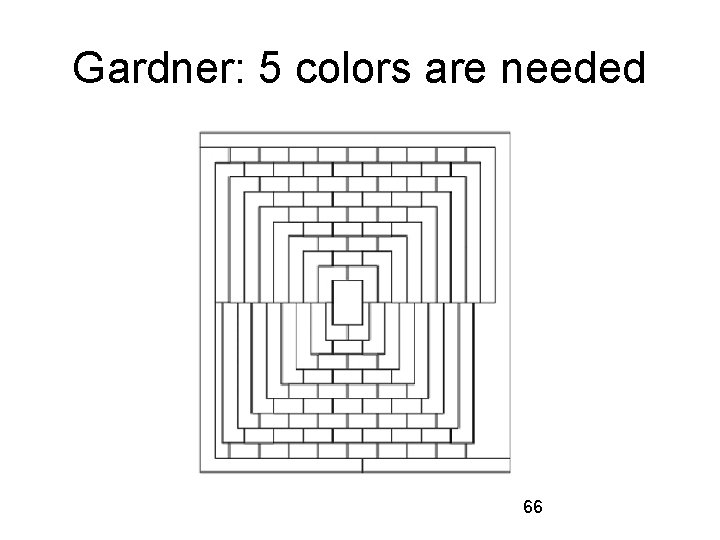
Maybe 4 colors aren't enough? What is needed to decide if 5 colors suffice? Just one map! And, of course, an accompanying argument showing that the map requires 5 colors. On 1975 April 1, Martin Gardner, editor for many years of the Mathematical Games column in Scientific American, published this map: 65

Gardner: 5 colors are needed 66

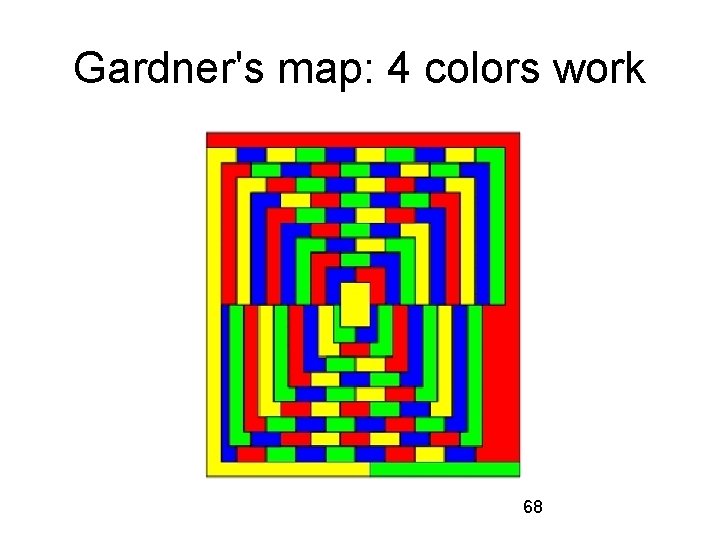
80+ years had gone by. . . What happened between 1890 and 1975? Lots. Many mathematicians tried their hands at proving the Four Color Conjecture. But none succeeded in finding a proof. Is that because 5 colors are needed? Is Gardner's map an example? Note again the date on his map: April 1. 67

Gardner's map: 4 colors work 68

At last! But a solution was near at hand. In 1976, Kenneth Appel (1932 -) and Wolfgang Haken (1928 -), two mathematicians at the University of Illinois at Urbana-Champaign, announced a proof. In 1977 in the Illinois Journal of Mathematics they published their proof: "Every Planar Map is Four Colorable”. 69

Some reactions “I am willing to accept the Appel-Haken proof – beggars cannot be choosers. ” “To most mathematicians, however, the proof of the four-color conjecture is deeply unsatisfactory. ” “God wouldn't let theorem be proved by a method as terrible as that!” 70

What's the problem? A key part of the proof was a computer program. It analyzed 1476 cases, requiring 1200 hours of machine time. Mathematicians were used to reading arguments presented in papers. How could they verify that the proof was correct? 71

Eventually: Acceptance “To reject the use of computers as what one may call 'computational amplifiers' would be akin to an astronomer refusing to admit discoveries made by telescope. ” “The things you can prove may be just tiny islands, exceptions, compared to the vast sea of results that cannot be proved by human thought alone. ” 72

In conclusion. . . To commemorate the proof, the University of Illinois adopted this postage meter stamp: 73

74
 When to use green's theorem vs stokes theorem
When to use green's theorem vs stokes theorem Map coloring prolog
Map coloring prolog Coloringws
Coloringws Leaf anatomy coloring key
Leaf anatomy coloring key Transcription end result
Transcription end result Skill 24 adjectives and adverbs
Skill 24 adjectives and adverbs Respiratory system coloring page
Respiratory system coloring page Adams food coloring
Adams food coloring Region coloring
Region coloring Is euglena living or nonliving
Is euglena living or nonliving Periodic table coloring activities
Periodic table coloring activities Periodic table coloring assignment
Periodic table coloring assignment Pentecost welcome
Pentecost welcome What did the onceler make
What did the onceler make What is an independent set in a graph
What is an independent set in a graph Hair color 101
Hair color 101 Dna and rna coloring worksheet
Dna and rna coloring worksheet Fahrenheit 451 pg 45-65
Fahrenheit 451 pg 45-65 Winter coloring page
Winter coloring page Anatomy and physiology coloring workbook chapter 14
Anatomy and physiology coloring workbook chapter 14 Balancing chemical equations coloring snowman
Balancing chemical equations coloring snowman A student obtains a liquid sample of green food coloring
A student obtains a liquid sample of green food coloring Label rock cycle
Label rock cycle Graph coloring problem
Graph coloring problem Graph coloring problem
Graph coloring problem What is graph coloring
What is graph coloring Pada kasus coloring banyak warna yang dipergunakan diminta
Pada kasus coloring banyak warna yang dipergunakan diminta Is adding food coloring to water a chemical change
Is adding food coloring to water a chemical change Homologous structures coloring worksheet
Homologous structures coloring worksheet Selinux coloring book
Selinux coloring book Stratum basale
Stratum basale Is a professional industry coined term
Is a professional industry coined term What is an adaptions
What is an adaptions Paper chromatography food coloring
Paper chromatography food coloring Face coloring in graph theory
Face coloring in graph theory Milk and food coloring lab report
Milk and food coloring lab report Factor theorem
Factor theorem Factor theorum
Factor theorum Remainder theorem
Remainder theorem Linear factors theorem and conjugate zeros theorem
Linear factors theorem and conjugate zeros theorem Rational root theorom
Rational root theorom Linear factors theorem and conjugate zeros theorem
Linear factors theorem and conjugate zeros theorem Hát kết hợp bộ gõ cơ thể
Hát kết hợp bộ gõ cơ thể Ng-html
Ng-html Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Voi kéo gỗ như thế nào
Voi kéo gỗ như thế nào Thang điểm glasgow
Thang điểm glasgow Chúa sống lại
Chúa sống lại Môn thể thao bắt đầu bằng từ chạy
Môn thể thao bắt đầu bằng từ chạy Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Công của trọng lực
Công của trọng lực Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Mật thư tọa độ 5x5
Mật thư tọa độ 5x5 Phép trừ bù
Phép trừ bù Phản ứng thế ankan
Phản ứng thế ankan Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Thể thơ truyền thống
Thể thơ truyền thống Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Một số thể thơ truyền thống
Một số thể thơ truyền thống Cái miệng xinh xinh thế chỉ nói điều hay thôi
Cái miệng xinh xinh thế chỉ nói điều hay thôi Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Nguyên nhân của sự mỏi cơ sinh 8
Nguyên nhân của sự mỏi cơ sinh 8 đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ Thế nào là giọng cùng tên
Thế nào là giọng cùng tên Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể Phối cảnh
Phối cảnh Thẻ vin
Thẻ vin đại từ thay thế
đại từ thay thế điện thế nghỉ
điện thế nghỉ Tư thế ngồi viết
Tư thế ngồi viết Diễn thế sinh thái là
Diễn thế sinh thái là Dot
Dot Số nguyên tố là gì
Số nguyên tố là gì