Rendering Matrix Transformations and the Graphics Pipeline CSE

Rendering – Matrix Transformations and the Graphics Pipeline CSE 3541/5541 Matt Boggus

Overview • • • Matrix format and operations Graphics pipeline overview Modeling transformations View and perspective transformations Polygon visibility and rasterization

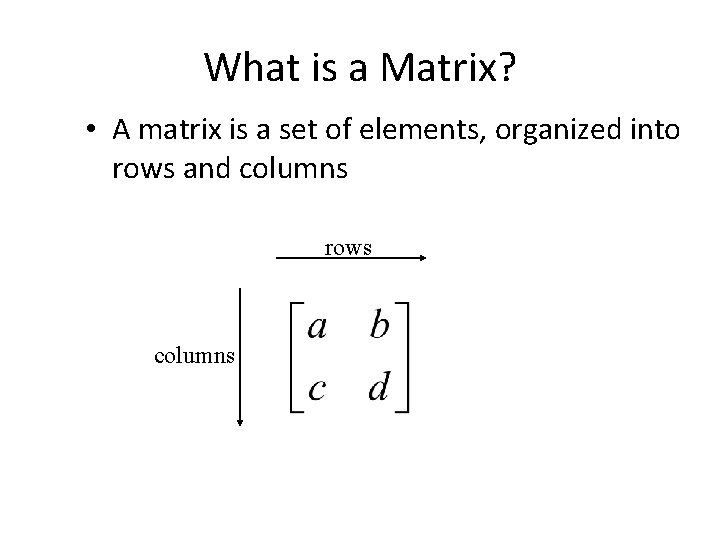
What is a Matrix? • A matrix is a set of elements, organized into rows and columns rows columns

Definitions • n x m Array of Scalars (n Rows and m Columns) – n: row dimension of a matrix, m: column dimension – m = n square matrix of dimension n – Element – Transpose: interchanging the rows and columns of a matrix • Column Matrices and Row Matrices – Column matrix (n x 1 matrix): – Row matrix (1 x n matrix):

Matrix Operations • Scalar‐Matrix Multiplication – Multiply every element by the scalar • Matrix‐Matrix Addition – Add elements with same index • Matrix‐Matrix Multiplication – A: n x l matrix, B: l x m C: n x m matrix cij = the sum of multiplying elements in row i of matrix a times elements in column j of matrix b

Matrix Operation Examples

Matrix Operations • Properties of Scalar‐Matrix Multiplication • Properties of Matrix‐Matrix Addition – Commutative: – Associative: • Properties of Matrix‐Matrix Multiplication • Identity Matrix I (Square Matrix)

Matrix Multiplication Order • Is AB = BA? Try it! • Matrix multiplication is NOT commutative! • The order of series of matrix multiplications is important!

Inverse of a Matrix • Identity matrix: AI = A • Some matrices have an inverse, such that: AA‐ 1 = I

Inverse of a Matrix • Do all matrices have a multiplicative inverse? Consider this example, try to solve for A‐ 1: AA‐ 100 = 0*a+0*d+0*g=0≠ 1 Note: 1 is the element at 00 in the identity matrix

Inverse of Matrix Concatenation • Inversion of concatenations (ABC)‐ 1 = ? A*B*C*X=I A * B * C‐ 1 = A * B * B‐ 1 = A A * A‐ 1 = I Order is important, so X = C‐ 1 B‐ 1 A‐ 1

Row and Column Matrices + points • Column Matrix – Row matrix • Concatenations – Associative • By Row Matrix By convention we will use column matrices for points

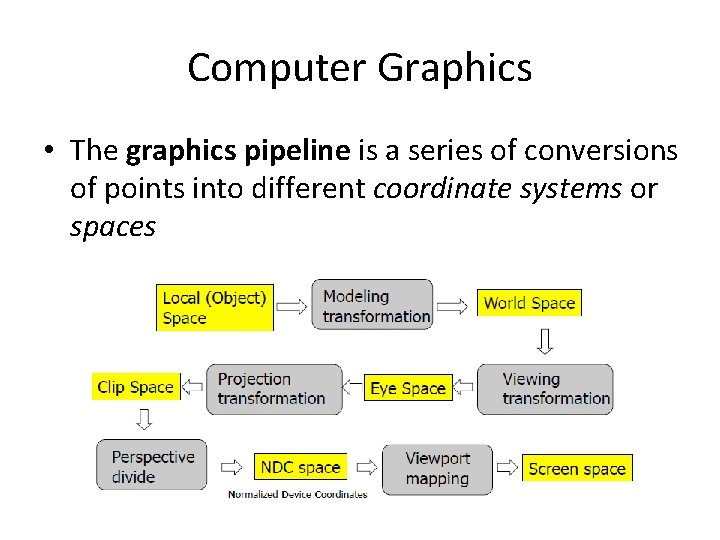
Computer Graphics • The graphics pipeline is a series of conversions of points into different coordinate systems or spaces

MODELING OR GEOMETRIC TRANSFORMATIONS

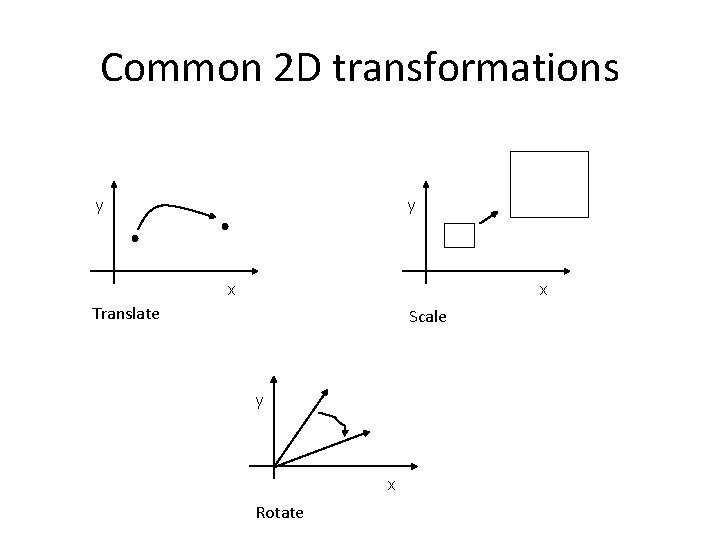
Common 2 D transformations y y x x Translate Scale y x Rotate

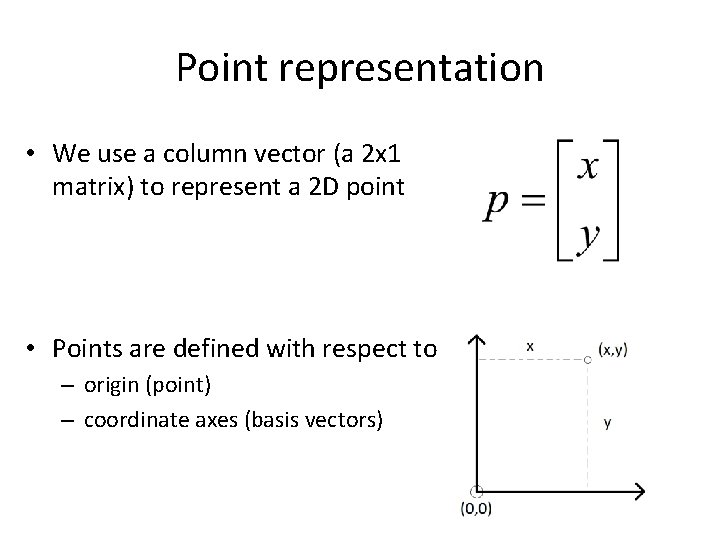
Point representation • We use a column vector (a 2 x 1 matrix) to represent a 2 D point • Points are defined with respect to – origin (point) – coordinate axes (basis vectors)

Arbitrary transformation of a 2 D point

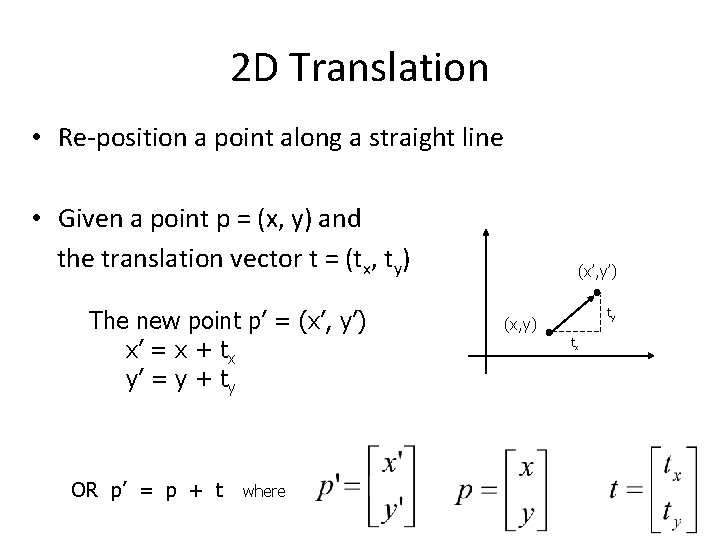
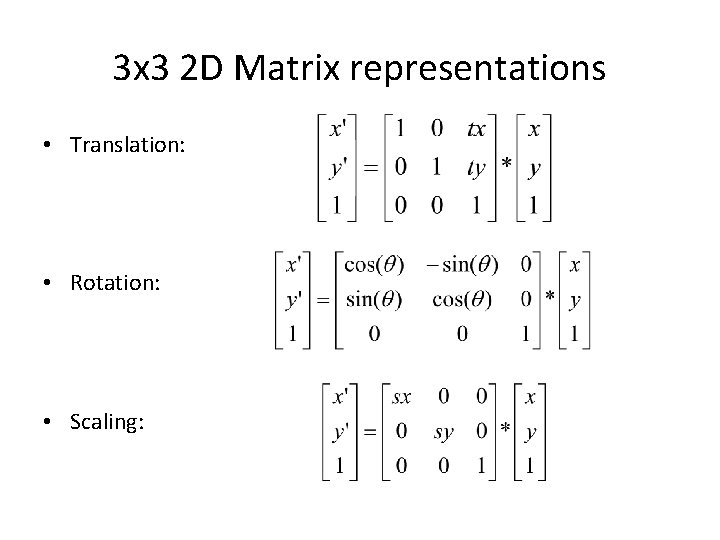
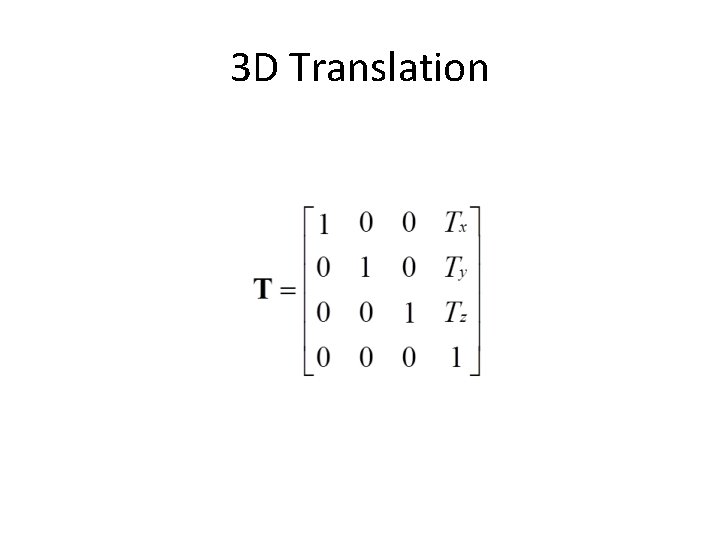
2 D Translation • Re‐position a point along a straight line • Given a point p = (x, y) and the translation vector t = (tx, ty) The new point p’ = (x’, y’) x’ = x + tx y’ = y + ty OR p’ = p + t where (x’, y’) ty (x, y) tx

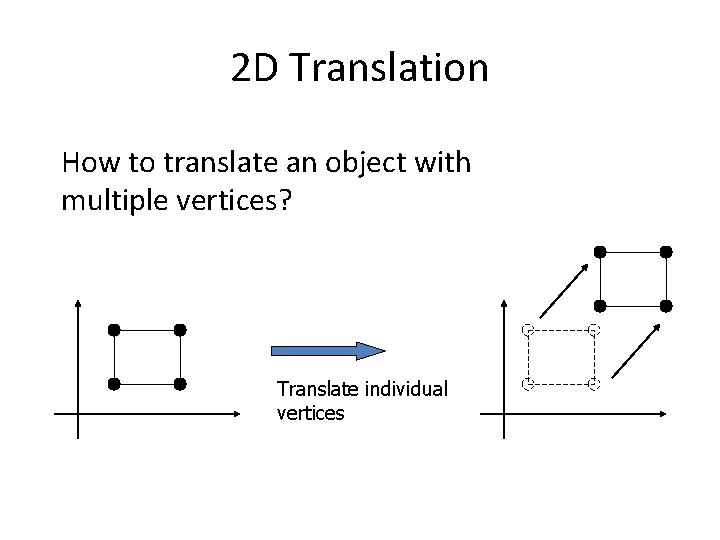
2 D Translation How to translate an object with multiple vertices? Translate individual vertices

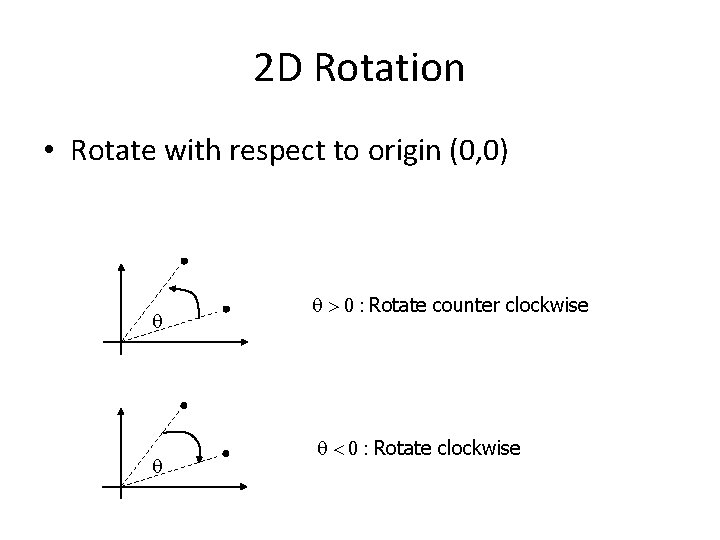
2 D Rotation • Rotate with respect to origin (0, 0) q q q > 0 : Rotate counter clockwise q < 0 : Rotate clockwise

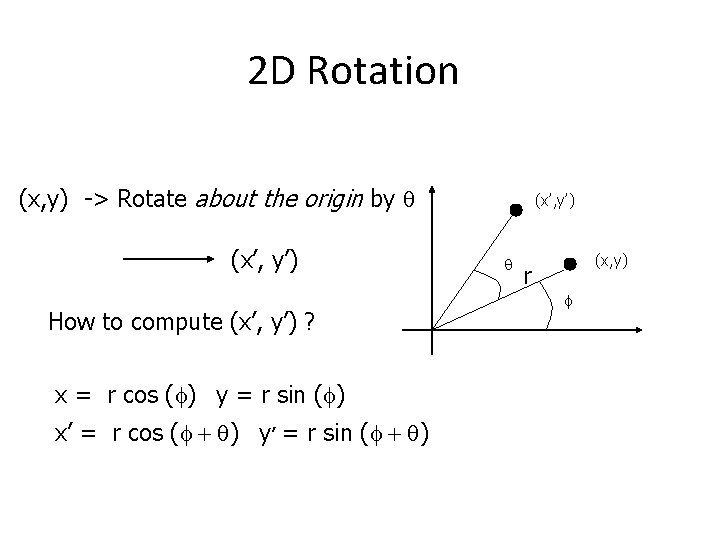
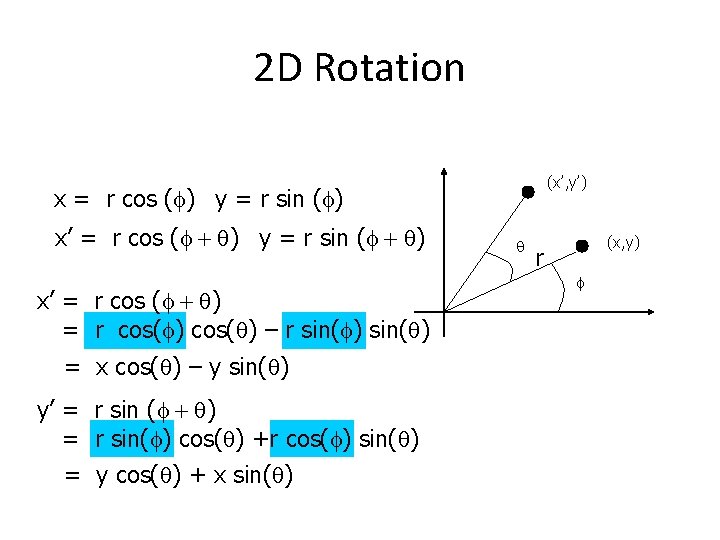
2 D Rotation (x, y) -> Rotate about the origin by q (x’, y’) How to compute (x’, y’) ? x = r cos (f) y = r sin (f) x’ = r cos (f + q) y’ = r sin (f + q) (x’, y’) q (x, y) r f

2 D Rotation (x’, y’) x = r cos (f) y = r sin (f) x’ = r cos (f + q) y = r sin (f + q) x’ = r cos (f + q) = r cos(f) cos(q) – r sin(f) sin(q) = x cos(q) – y sin(q) y’ = r sin (f + q) = r sin(f) cos(q) +r cos(f) sin(q) = y cos(q) + x sin(q) q (x, y) r f

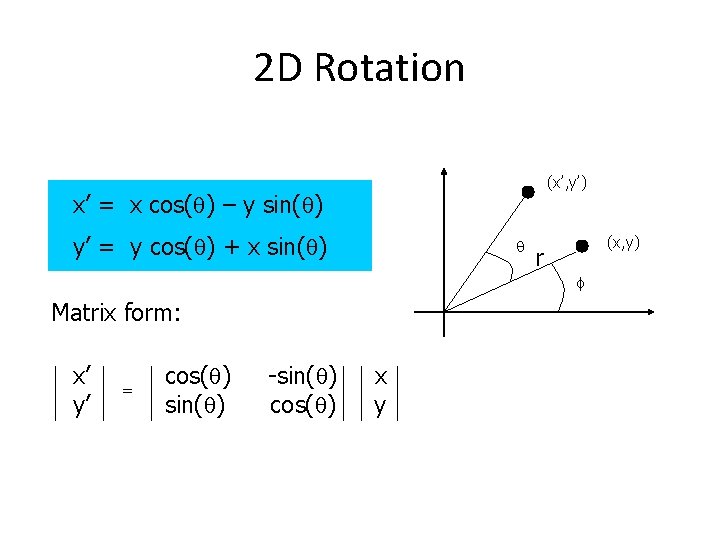
2 D Rotation (x’, y’) x’ = x cos(q) – y sin(q) y’ = y cos(q) + x sin(q) q (x, y) r f Matrix form: x’ y’ = cos(q) sin(q) -sin(q) cos(q) x y

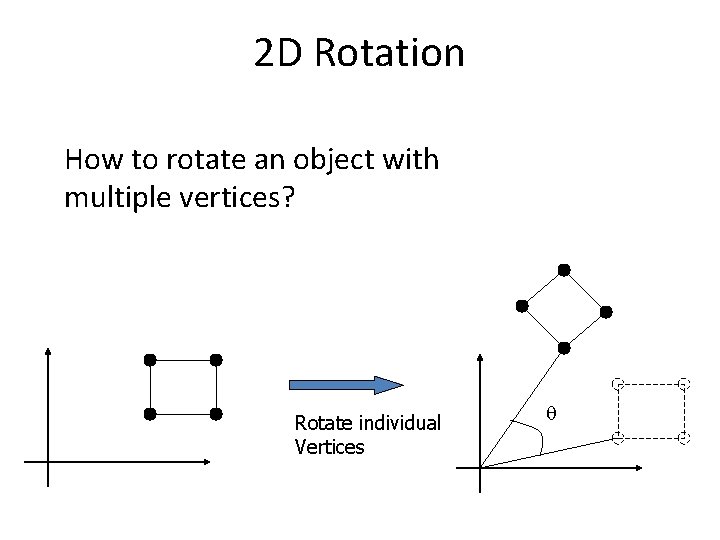
2 D Rotation How to rotate an object with multiple vertices? Rotate individual Vertices q

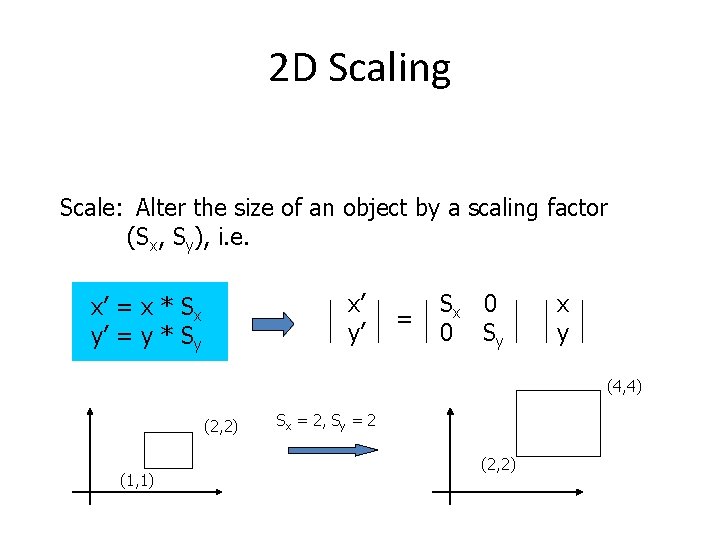
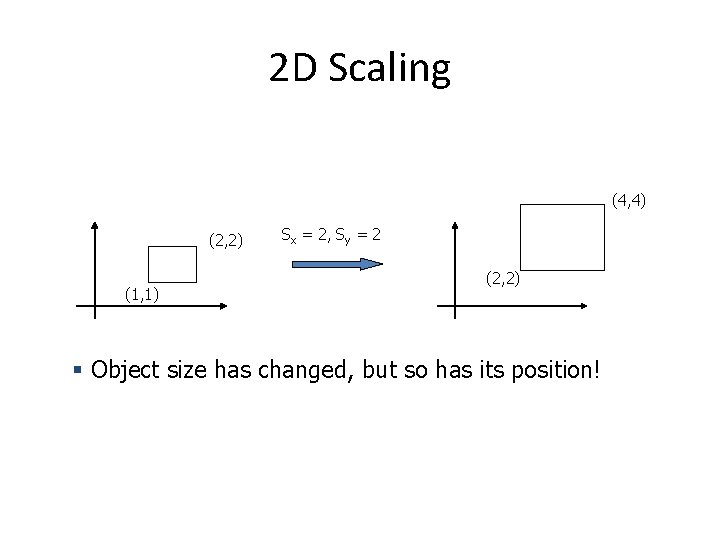
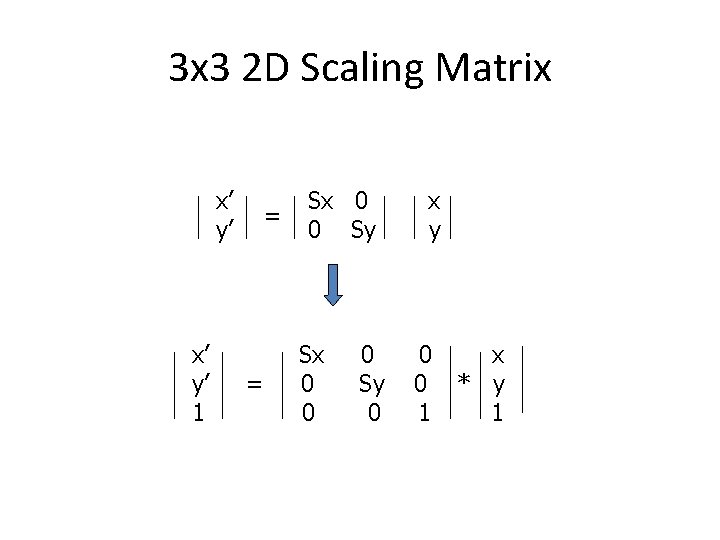
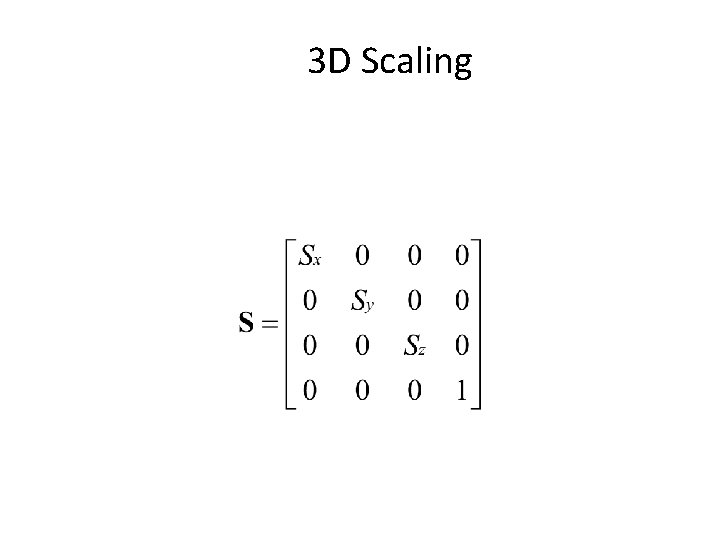
2 D Scaling Scale: Alter the size of an object by a scaling factor (Sx, Sy), i. e. x’ y’ x’ = x * Sx y’ = y * Sy = Sx 0 0 Sy x y (4, 4) (2, 2) (1, 1) Sx = 2, Sy = 2 (2, 2)

2 D Scaling (4, 4) (2, 2) (1, 1) Sx = 2, Sy = 2 (2, 2) § Object size has changed, but so has its position!

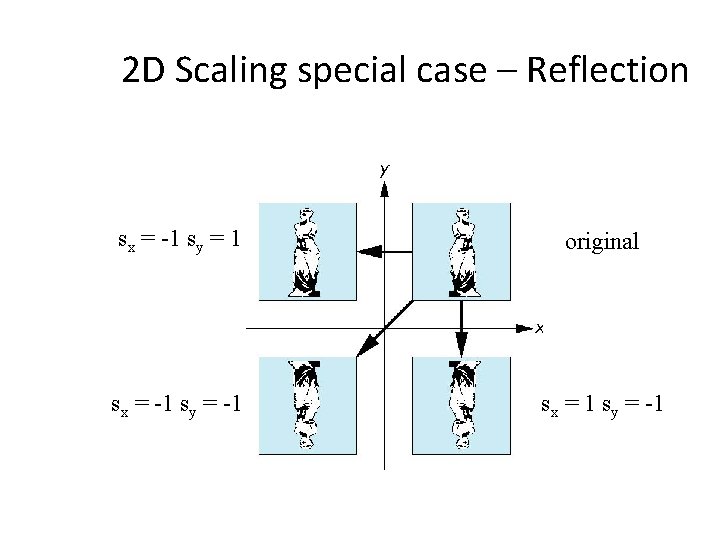
2 D Scaling special case – Reflection sx = -1 sy = 1 original sx = -1 sy = -1 sx = 1 sy = -1

Put it all together • Translation: x’ x = y’ y • Rotation: • Scaling: + tx ty x’ cos(q) ‐sin(q) x = * y’ sin(q) cos(q) y x’ y’ Sx = 0 0 x * Sy y

Translation as multiplication? Can we use only tx and ty to make a multiplicative translation matrix? (Boardwork derivation)

Translation Multiplication Matrix x’ y’ = x y + tx ty Use 3 x 1 vector x’ y’ 1 = 1 0 0 0 1 0 tx ty 1 * x y 1

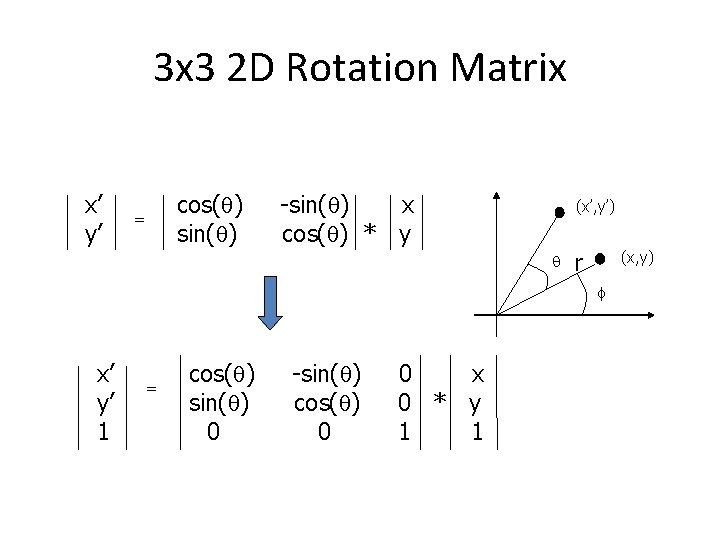
3 x 3 2 D Rotation Matrix x’ y’ cos(q) sin(q) = -sin(q) x cos(q) * y (x’, y’) q r (x, y) f x’ y’ 1 = cos(q) sin(q) 0 -sin(q) cos(q) 0 0 x 0 * y 1 1

3 x 3 2 D Scaling Matrix x’ y’ 1 = = Sx 0 0 Sy Sx 0 0 0 Sy 0 x y 0 0 1 x * y 1

3 x 3 2 D Matrix representations • Translation: • Rotation: • Scaling:

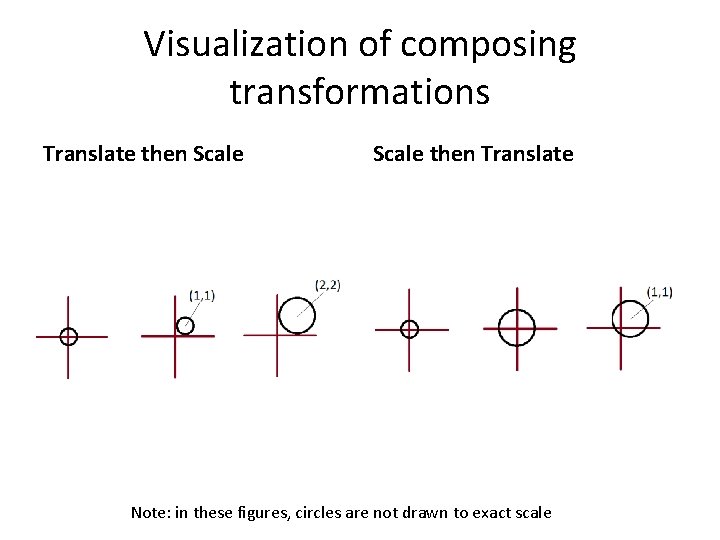
Visualization of composing transformations Translate then Scale then Translate Note: in these figures, circles are not drawn to exact scale

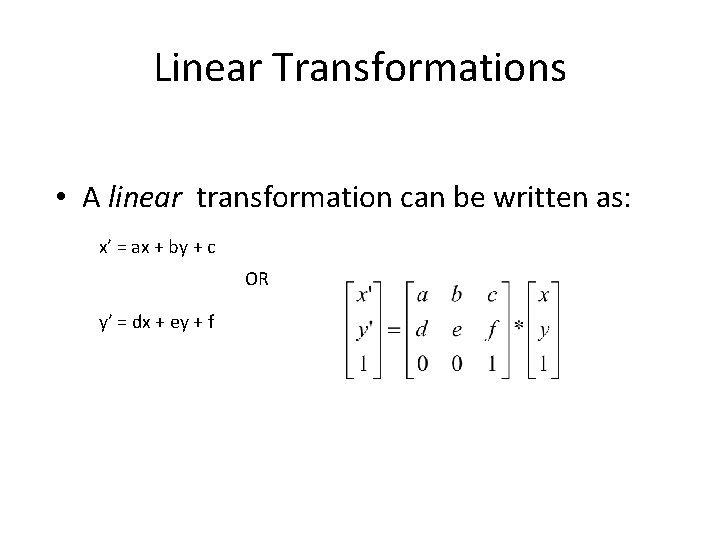
Linear Transformations • A linear transformation can be written as: x’ = ax + by + c OR y’ = dx + ey + f

Why use 3 x 3 matrices? • So that we can perform all transformations using matrix/vector multiplications • This allows us to pre-multiply all the matrices together • The point (x, y) is represented using Homogeneous Coordinates (x, y, 1)

Matrix concatenation • Examine the computational cost of using four matrices ABCD to transform one or more points (i. e. p’ = ABCDp) • We could: apply one at a time – – p' = D * p p'' = C * p' … 3 x 3 * 3 x 1 for each transformation for each point • Or we could: concatenate (pre-multiply matrices) – – M=A*B*C*D p' = M * p 3 x 3 * 3 x 3 for each transformation 3 x 3 * 3 x 1 for each point

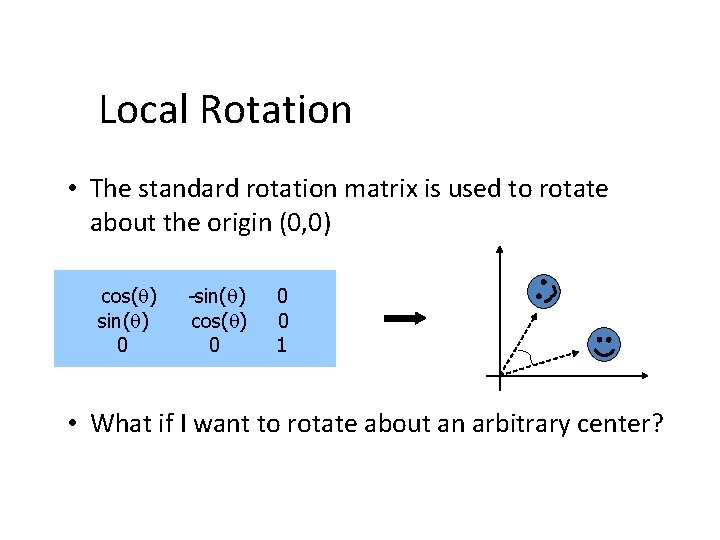
Local Rotation • The standard rotation matrix is used to rotate about the origin (0, 0) cos(q) sin(q) 0 -sin(q) cos(q) 0 0 0 1 • What if I want to rotate about an arbitrary center?

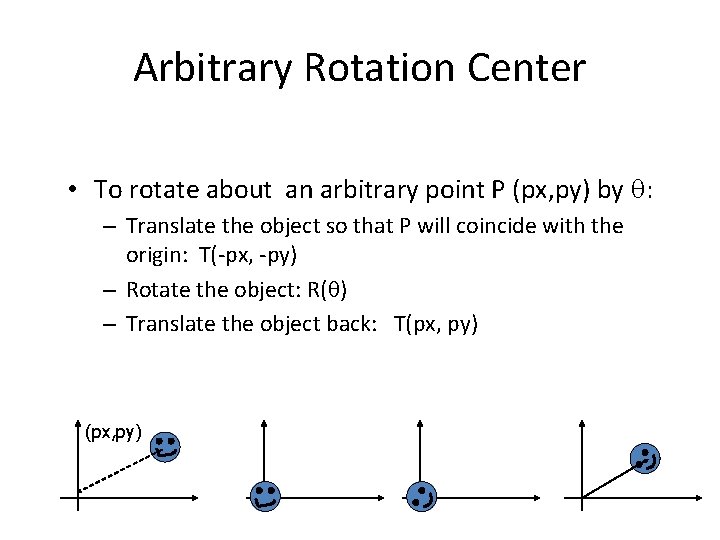
Arbitrary Rotation Center • To rotate about an arbitrary point P (px, py) by q: – Translate the object so that P will coincide with the origin: T(‐px, ‐py) – Rotate the object: R(q) – Translate the object back: T(px, py)

Arbitrary Rotation Center • Translate the object so that P will coincide with the origin: T(‐ px, ‐py) • Rotate the object: R(q) • Translate the object back: T(px, py) • As a matrix multiplication • p’ = T[px, py] * R[q] * T[‐px, ‐py] * P x’ y’ = 1 1 0 px 0 1 py 00 1 cos(q) -sin(q) 0 sin(q) cos(q) 0 0 0 1 1 0 -px 0 1 -py 0 0 1 x y 1

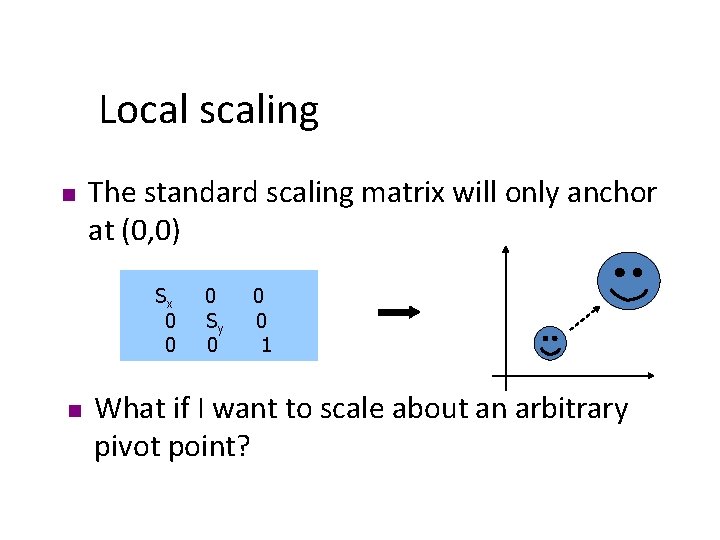
Local scaling n The standard scaling matrix will only anchor at (0, 0) Sx 0 0 n 0 Sy 0 0 0 1 What if I want to scale about an arbitrary pivot point?

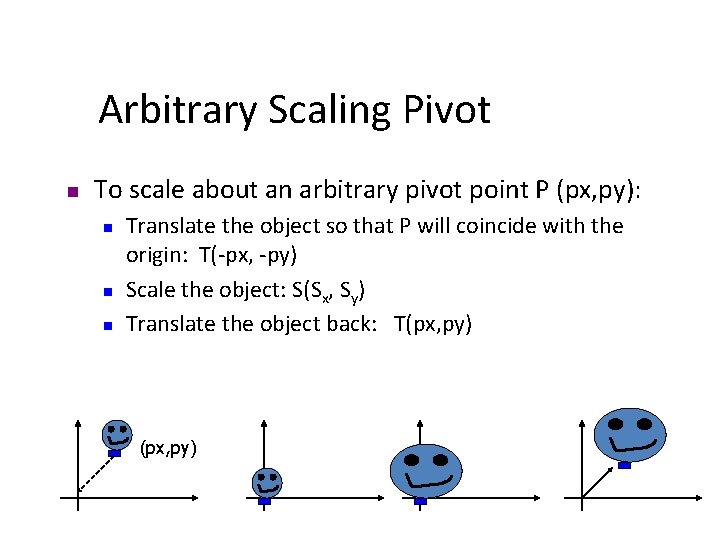
Arbitrary Scaling Pivot n To scale about an arbitrary pivot point P (px, py): n n n Translate the object so that P will coincide with the origin: T(‐px, ‐py) Scale the object: S(Sx, Sy) Translate the object back: T(px, py)

Moving to 3 D • Translation and Scaling are very similar, just include z dimension • Rotation is more complex

3 D Translation

3 D Scaling

3 D Rotations – rotation about primary axes

VIEWING AND PROJECTION TRANSFORMATIONS

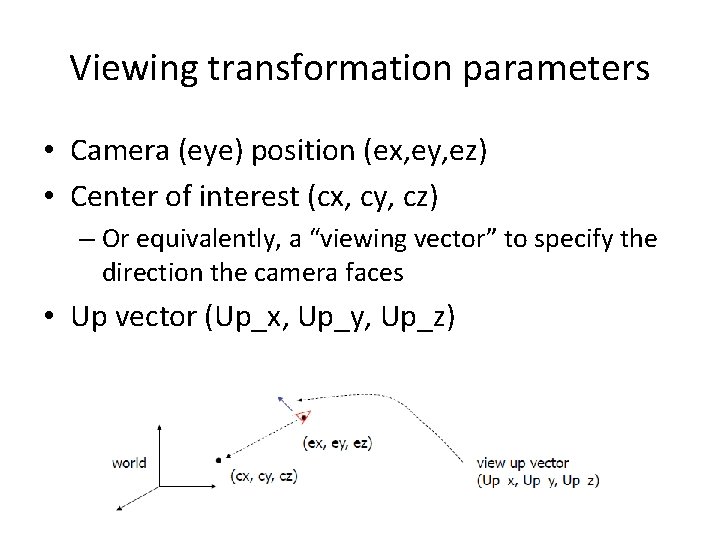
Viewing transformation parameters • Camera (eye) position (ex, ey, ez) • Center of interest (cx, cy, cz) – Or equivalently, a “viewing vector” to specify the direction the camera faces • Up vector (Up_x, Up_y, Up_z)

Eye coordinate system • • Camera (eye) position (ex, ey, ez) View vector : v Up vector : u Third vector (v x u) : w • Viewing transform – construct a matrix such that: – Camera is translated to the origin – Camera is rotated so that • v is aligned with (0, 0, 1) or (0, 0, ‐ 1) • u is aligned with (0, 1, 0)

Projection • Transform a point from a high dimensional space to a low‐dimensional space. • In 3 D, the projection means mapping a 3 D point onto a 2 D projection plane (or called image plane). • There are two basic projection types: – Parallel (orthographic) – Perspective

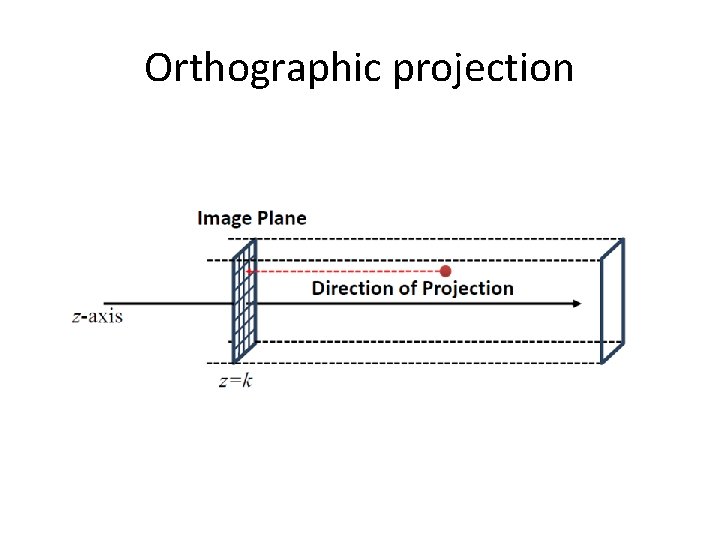
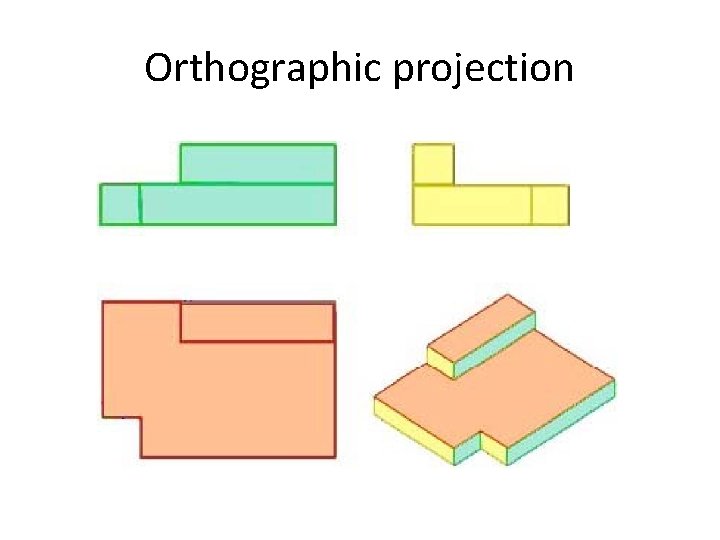
Orthographic projection

Orthographic projection

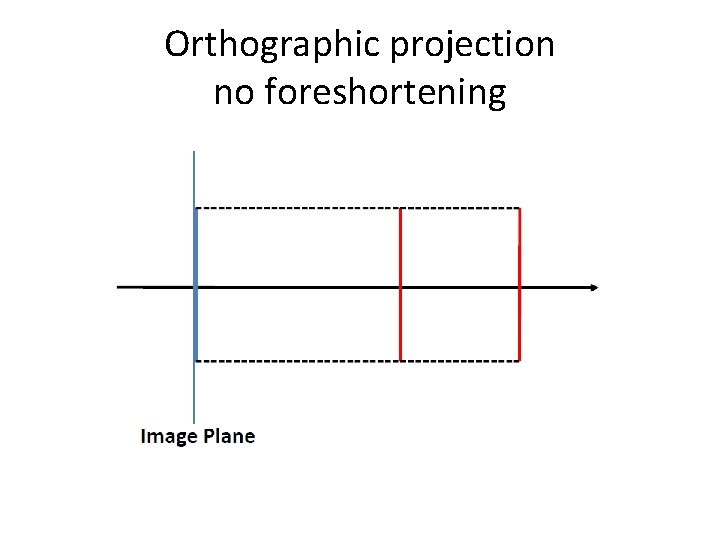
Properties of orthographic projection • • • Not realistic looking Can preserve parallel lines Can preserve ratios Does not preserve angles between lines Mostly used in computer aided design and architectural drawing software

Foreshortening – Pietro Perugino fresco example

Orthographic projection no foreshortening

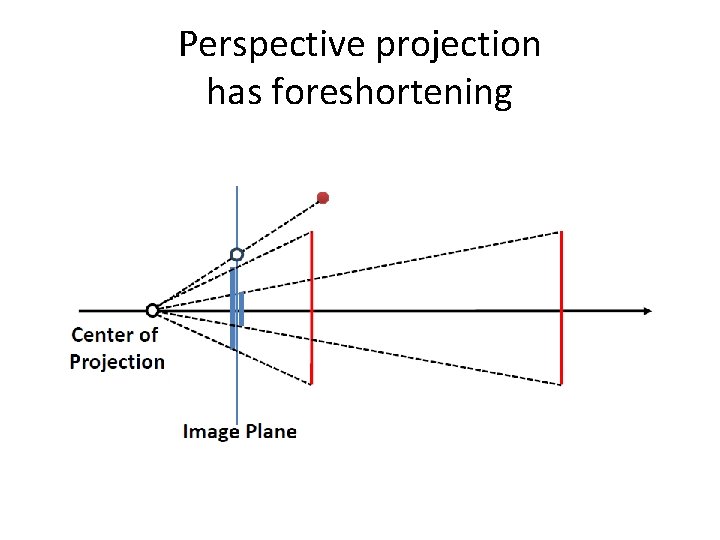
Perspective projection has foreshortening

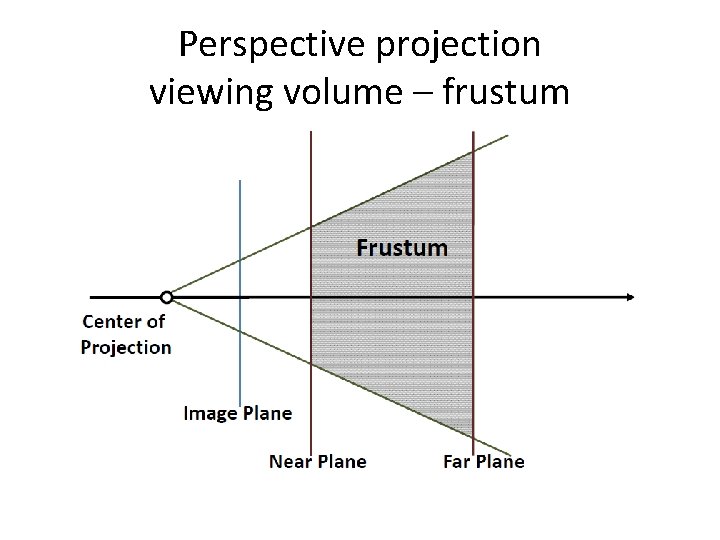
Perspective projection viewing volume – frustum

Properties of perspective projection • • • Realistic looking Lines are mapped to lines Parallel lines may not remain parallel Ratios are not preserved Distances cannot be directly measured, as in parallel projection

VISIBILITY AND RASTERIZATION

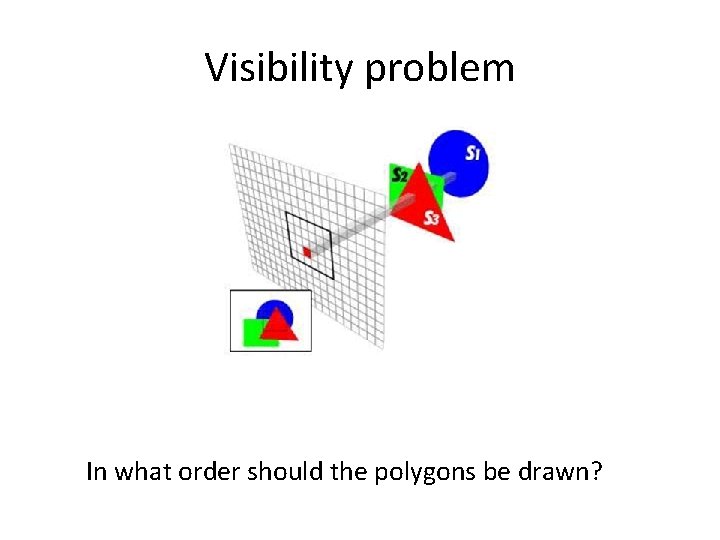
Visibility problem In what order should the polygons be drawn?

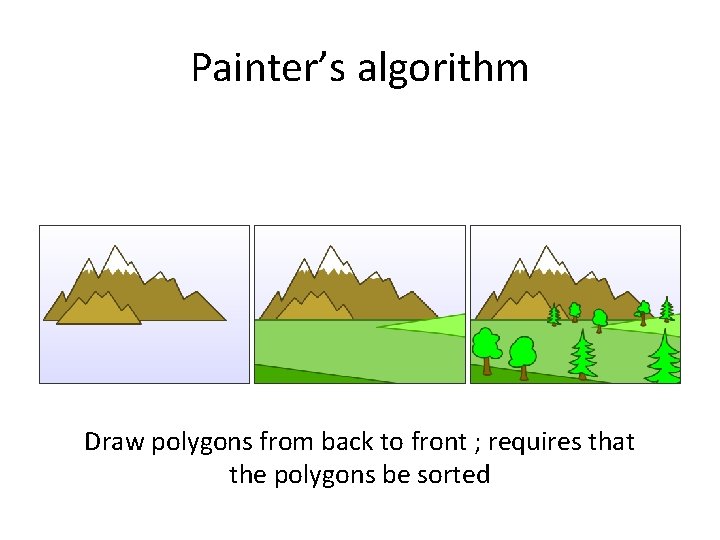
Painter’s algorithm Draw polygons from back to front ; requires that the polygons be sorted

Z‐buffer, with example • Foreach polygon – Foreach pixel in polygon • Compare polygon depth at (x, y) with current depth at (x, y) • If( polygon. z < midepth) – Set mindepth – Set pixel as polygon’s color

ADDITIONAL SLIDES

Critical thinking – transformations and matrix multiplication • Suppose we want to scale an object, then translate it. What should the matrix multiplication look like? A. B. C. D. p’ = Scale * Translate * p p’ = Translate * Scale * p p’ = p * Scale * Translate Any of these is correct

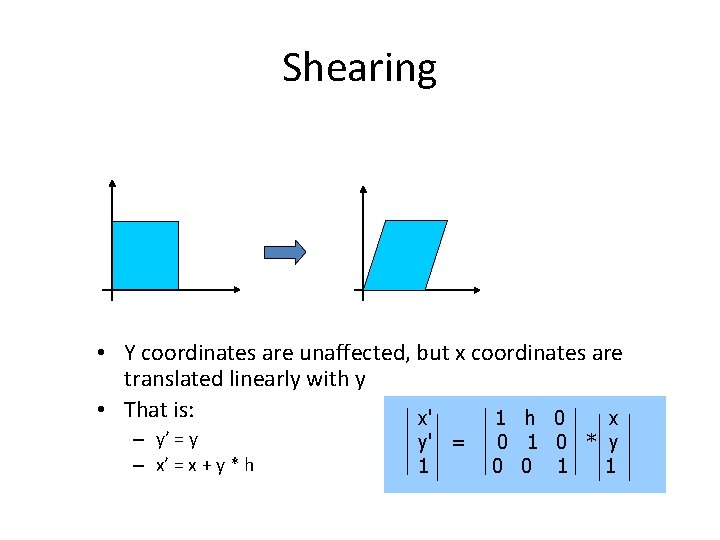
Shearing • Y coordinates are unaffected, but x coordinates are translated linearly with y • That is: x' 1 h 0 x – y’ = y – x’ = x + y * h y' = 1 0 * y 0 0 1 1

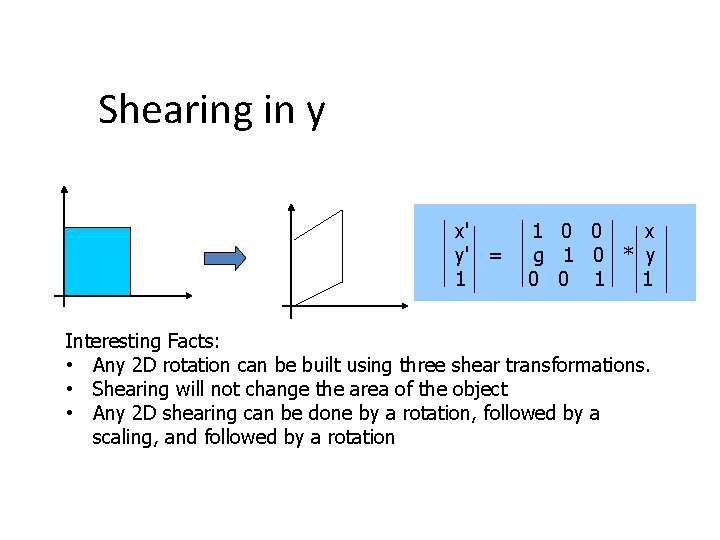
Shearing in y x' y' = 1 1 0 0 x g 1 0 * y 0 0 1 1 Interesting Facts: • Any 2 D rotation can be built using three shear transformations. • Shearing will not change the area of the object • Any 2 D shearing can be done by a rotation, followed by a scaling, and followed by a rotation

Another use of perspective • Head Tracking for Desktop VR Displays using the Wii. Remote