Matrix and Graph Matrix Binary Matrix Sparse Matrix

Matrix and Graph • Matrix • Binary Matrix • Sparse Matrix • Operations for Vectors/Matrices • Graph and Adjacent Matrix • Adjacent List

Matrix and Graph • Matrix is a 2 -dimensional structure • Used in wide areas from physical simulations to customer management • Graphs are also used in many areas, to represent the relations and flows between data • Some data structures have been considered to handle matrix and graph; update, preserve, search, and operate

2 -Dimensional Structure of Matrix • An n×m matrix has n×m numbers 　 can be stored in an array of size n×m 　[i, j] element corresponds to the i*m+j th cell of the array 　　 • A naïve design is done, but there are something more

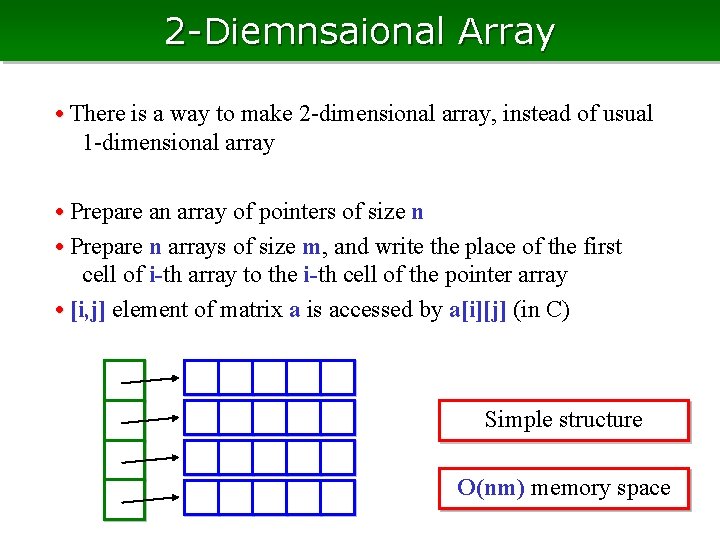
2 -Diemnsaional Array • There is a way to make 2 -dimensional array, instead of usual 1 -dimensional array • Prepare an array of pointers of size n • Prepare n arrays of size m, and write the place of the first cell of i-th array to the i-th cell of the pointer array • [i, j] element of matrix a is accessed by a[i][j] (in C) 　　 Simple structure O(nm) memory space

Allocate a 2 -Dimensional Array int *MATRIX_alloc ( int n, int m ){ int i, **a, flag =0; a = malloc ( sizeof(int *)*n ); if ( a=NULL ) return (NULL); for ( i=0 ; i<n ; i++ ){ a[i] = malloc (sizeof(int)*m); if ( a[i] = NULL ) flag = 1; } if ( flag == 1 ) return (NULL); else return (a); } int *MATRIX_free ( int **a ){ int i; for ( i=0 ; i<n ; i++ ) free ( a[i] ); }

Binary Matrix • A binary matrix is a matrix all whose cells are either 0 or 1 　+ each cell is either ○ or × 　+ adjacency matrix of a graph, shown later • Space consuming if use one integer for one 01 value (1 bit) 　 motivated to compress the matrix ０１０１０ １０００１ １１１１０ １１０００

Representation by Bits • A row composed of 01 values can be considered as a big integer by chopping into some integers of 32 bits (or 64 bits), the integer becomes tractable └m/32┘ integers are sufficient to store a row 　　 (space efficiency also increases, and also cache efficiency) • [i, j] element can be accessed by looking at the (j%32)th bit of the j/32 th integer in the i-th row

Handling Bit Access • [i, j] element can be accessed by looking at the (j%32)th bit of the j/32 th integer in the i-th row … writing a code is bothering • Prepare an array BIT_MASK[]= {1, 2, 4, 8, 16, …} BIT_MASK_[]= {0 xfffffffe, 0 xfffffffd, 0 xfffffffb, …} + read value: a[i][j/32] & BITMASK[j%32] + set to 1 : a[i][j/32] = a[i][j/32] | BITMASK[j%32] + set to 0 : a[i][j/32] = a[i][j/32] & BITMASK_[j%32]

Sparse Matrix • That’s all, for structures for simple matrices • Space efficiency is in some sense optimal • But, in application, it is often not sufficient/efficient 　 for example, if matrix is sparse, many parts are redundant • Sparse matrix has the same value in many cells (usually 0) • Sparse matrix should be stored by memorizing the places with non-zero values

Storing Sparse Matrix • Let’s begin from binary matrix, for simplicity 　 almost cells are 0, and few 1’s • A simple idea is to make a list of the places of the cells being 1 • That is, memorize (x 1, y 1), (x 2, y 2), (x 3, y 3), … , store the row ID and column ID of the cells being 1 • The memory requirement is “twice the number of 1’s” this is very efficient if there are few 1’s (sparse) • But, bad accessibility; to read a cell, we have to scan all (binary tree / hash can be used)

Store Row-wise • Let’s have a structure to improve the accessibility • Classify the places of 1’s according to their row ID 　 prepare n arrays, and store the column ID of 1’s in i-th row, in the ith array • We need to have n pointers to n arrays, but we don’t have to store the row ID’s, thus memory efficiency increases • The memory requirement is “# 1’s ＋ #rows× 2” (can be “# 1’s ＋ #rows”) • Accessibility is good; sorting ID’s in a row array, binary search works (linear scan is enough, if few column ID’s)

Structure in Each Row • In sparse cases, the efficiency is increased, However, the update concerned with insertion/deletions is not efficient • They are the same, in the situation of stacks and queues • So, according to the purpose, we use lists bucket/hash/binary tree for structures in a row 　(having n arrays is equivalent to having buckets)

Real World Data • The characteristics of sparse matrices in practice are; + Matrix representing mesh network (structural calculation) few meshes are adjacent to one, in geometrical sense, thus not so many non-zeros per row array is sufficient for structures of rows + Road network data (adjacency of cross points + distance) 　 almost the same, but update comes sometimes (would be sufficient if (re-)allocate bit larger memory)

Real World Data (2) Ex) A matrix representing, row text, column word, a cell is one if the word is included in the text, is sparse, usually 　(POS data, Web links, Web surfing, etc. ) + on average, #1’s in a row/column is constant, but some have so many　(texts having many words, words included in many texts) + distribution of 1’s is that so called power (zip) law, scale free; #of items of size D is proportional to 1 / ΔD can be often seen in real world data (≠ geometric distribution) + Such data needs algorithms designed so that the dense part will not affect badly; will be the bottle neck of the computation

Non-binary Sparse Matrix • Usual matrix are of course non-binary, it is not sufficient to remember the places having non-zero value remember (place, value) • In the case of using array, (place, value), …, or place 1, plcae 2, …, value 1, value 2, … • In the case of lists of binary tree, assign (place, value) to each cell/node or, simple prepare two of them

Exercise • Make data representing the following matrix in a sparse way 0, 0, 1, 4, 0 0, 1, 0, 0, 5 2, 0, 0 1, 2, 5, 0, 2 0, 0, 0

Column: Memory Saving for Matrix • Buckets, or a row of a sparse matrix needs two data (pointer to the first cell, and the size ki) • We decrease these from two to one • First, prepare an array of size equal to # non-zero cells. Then, + 0 th row uses the cells of the array ranging from 0 to k 0 -1 + 1 st uses from k 0 to k 0+k 1 -1 … + i-th row uses from k 0+…+ki-1 to k 0+…+ki-1, and we remember only the start positions of the rows • The size of i-th row can be obtained by (start position of i+1) - (start position of i)

Matrix Operation • Basic matrix operations are addition and multiplication (inner product of vectors is a special case) Further, AND and OR for binary matrix • Algorithms for the operations are trivial if the matrices are in the form of 2 -dimensional array However, not clear if they are in sparse forms • Further, there are several structures that have advances for matrix operations

Addition of Matrix • For the addition, it is sufficient to have algorithms for additions of each row (so, operations of vectors are sufficient) • First, we see the case of inner product of sparse vectors

Inner Product • For computing inner product of two sparse vectors, the difficulty is that we have to find the cell corresponding to each • Sort the cells in each vector according to their column ID • Scan two vectors simultaneously, from smaller indices 　“simultaneously” means that iteratively pick up the smallest column ID among the two vectors • When we find a column ID at which both vector have non-zero values, accumulate the product of the cells 1 5 5 1 7 3 1 1 3 3 5 4

A Code for Sparse Inner Product int SVECTOR_innerpro (int *va, int ta, int *vb, int tb){ int ia=0, ib=0, c=0; while ( ia<ta && ib<tb){ if (va[ia*2] < vb[ib*2] ) ia++; else if (va[ia*2] > vb[ib*2] ) ib++; else { c = c + va[ia*2+1]*vb[ib*2+1]; ia++; ib++; } } return ( c ); } 1 5 5 1 7 3 2 1 3 3 5 4

Addition of Two Vectors • The addition can be done in a similar way • Sort the cells in each vector according to their column ID • Scan two vectors simultaneously, from smaller indices • The positions of non-zero values in the resulted vectors are those having non-zero values in one of two vectors, thus can be easily identified by the scan 1 5 5 1 7 3 2 1 3 3 5 4

A Code for Addition int SVECTOR_add (int *vc, int *va, int ta, int *vb, int tb){ int ia=0, ib=0, ic=0, c, cc; while ( ia<ta || ib<tb){ if (ia == ta ){ c = vb[ib*2+1]; cc = vb[ib*2]; ib++; } else if ( ib == tb ){c = va[ia*2+1]; cc = va[ia*2]; ia++; } else if (va[ia*2] > vb[ib*2] ) { c = vb[ib*2+1]; cc = vb[ib*2]; ib++; } else if (va[ia*2] < vb[ib*2] ) { c = va[ia*2+1]; cc = va[ia*2]; ia++; } else { c = va[ia*2+1] + vb[ib*2+1]; cc = vb[ib*2]; ia++; ib++; } vc[ic*2] = cc; vc[ic*2+1] = c; ic++; } return ( ic ); } 1 5 5 1 7 3 2 1 3 3 5 4

Column: Endmarks do a Good Job! • Compared to inner product, code for addition is relatively long we have exceptions at the end of the array • So, we are motivated to simplify the code by using “endmark” (endmark is a symbol that represent the end of the array, or something else representing the end) • 0, -1 or a very large value is used as an endmark • We prepare an additional cell next to the end of each array, and put an endmark at the cell

Column: Endmarks do a Good Job! (2) int SVECTOR_innerpro (int *vc, int *va, int ta, int *vb, int tb){ int ia=0, ib=0, ic=0, c, cc; while ( va[ia*2] != ENDMARK && vb[ib*2] != ENDMARK){ if (va[ia*2] > vb[ib*2] ) { c = vb[ib*2+1]; cc = vb[ib*2]; ib++; } else if (va[ia*2] < vb[ib*2] ) { c = va[ia*2+1]; cc = va[ia*2]; ia++; } else { c = va[ia*2+1] + vb[ib*2+1]; cc = vb[ib*2]; ia++; ib++; } vc[ic*2] = cc; vc[ic*2+1] = c; ic++; } vc[ic*2] = ENDMARK; return ( ic ); 1 5 5 1 7 3 ■ } 2 1 3 3 5 4 ■

Matrix Multiplication • For sparse matrix multiplication, compute the inner products of all the pairs of a row and a column • However, a sparse matrix has row representations but not column representations, getting column vectors is hard • A simple solution is to use transposing algorithm that is explained in the section of bucket; we will have column representation • On the other hand, some data structures are designed to be enabled to trace also columns

Four-Direction List • Lists are good at storing sparse vectors, for tracing • However, collection of lists isn’t good at tracing column vectors, because the cells are not connected vertically • …so, let’s have a list connected in both row direction and column direction • Each cell has four arms, that point the neighboring cells in directions of (←, →, ↑, ↓) 4 7 2

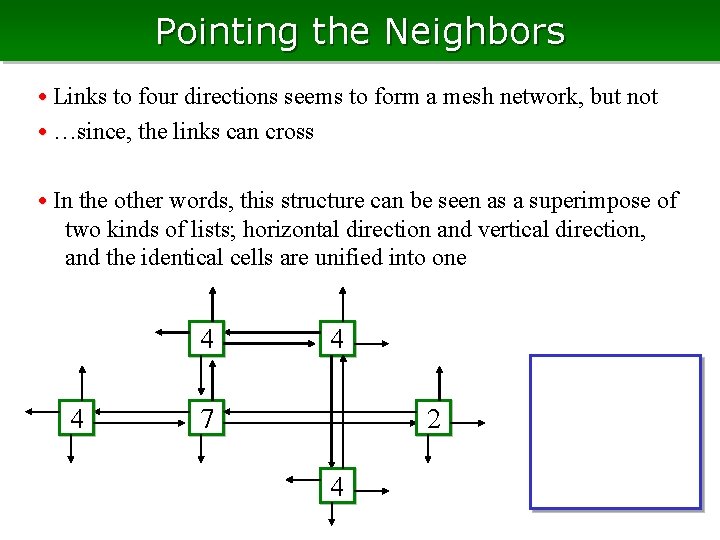
Pointing the Neighbors • Links to four directions seems to form a mesh network, but not • …since, the links can cross • In the other words, this structure can be seen as a superimpose of two kinds of lists; horizontal direction and vertical direction, and the identical cells are unified into one 4 4 4 7 2 4

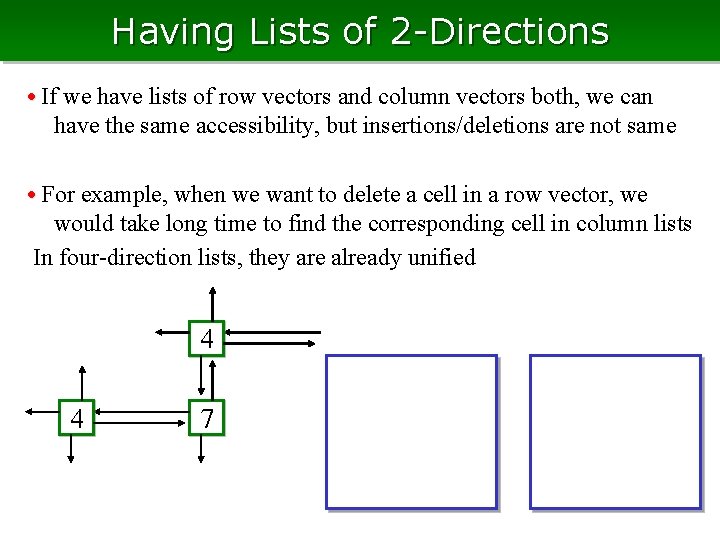
Having Lists of 2 -Directions • If we have lists of row vectors and column vectors both, we can have the same accessibility, but insertions/deletions are not same • For example, when we want to delete a cell in a row vector, we would take long time to find the corresponding cell in column lists In four-direction lists, they are already unified 4 4 7

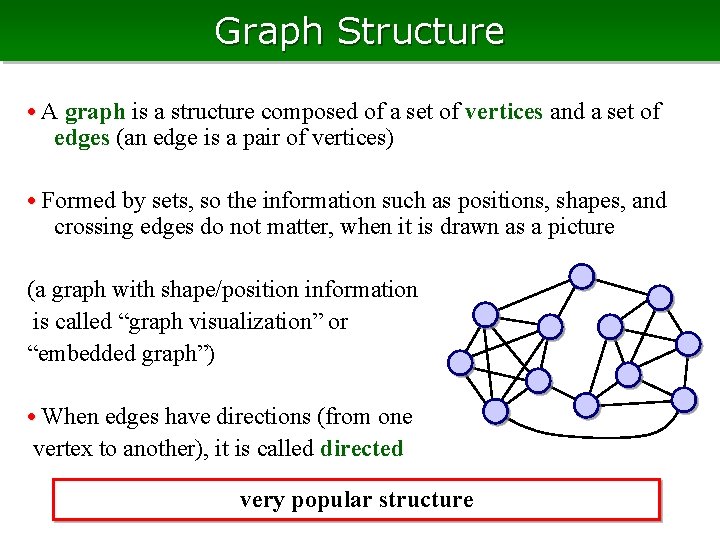
Graph Structure • A graph is a structure composed of a set of vertices and a set of edges (an edge is a pair of vertices) • Formed by sets, so the information such as positions, shapes, and crossing edges do not matter, when it is drawn as a picture 　 (a graph with shape/position information is called “graph visualization” or “embedded graph”) • When edges have directions (from one vertex to another), it is called directed very popular structure

Examples of Graph Data • Adjacency relation Hierarchy in an organization Similarity relation • Web network, human network, SNS friend network, …

Graph Terminology • Edge e is said to be incident to u, v, and vice versa, if e = (u, v) also u and v are said to be adjacent • The #edges incident to v is the degree of v • A graph having edges for any two vertices is a complete graph • When there are two or more edges connecting two vertices, the edges are called multiple edges • If there is a partition of vertices so that any edge connects a vertex in a group and one in the other, the graph is called bipartite graph

Storing a Graph • n vertices can be seen as numbers 0, …, n-1 • Then, an edge is a pair of numbers can be stored by writing the pairs in array, lists, etc. • Further, we need something for the accessibility for example, we often visit a vertex, and go to the neighboring vertex, and so we need to scan all edges incident to the vertex

Using Matrix • The set of edges can be represented by a matrix as follows ① j-th row/column corresponds to vertex j, and ij-cell is 1 if there is edge (i, j) (called adjacency matrix) 　+ efficient for dense graph having many edges + multiplicity of edges can be represented by the value of a cell ② j-th row corresponds to vertex j, and each column corresponds to an edge; when edge e is incident to vertex i, ij cell is 1 (called incidence matrix) + multiple edges represented easily • Sparse matrix representation has advantage for incidence matrix and sparse graph

In Practice • 2 -dimensional array is sufficient when the matrix size is small the cost is small, redundancy is small • Sparse matrix such as 100 by 100 with 10 non-zero elements in a row, sparse representation will be efficient (approximately, when density is less than 10%) + When we often want to scan non-zero elements, such as tracing all vertices adjacent to a vertex, sparse representation is useful + If we want to check whethere is an edge between two specified vertices, 2 -dimensional array has advantage

Incidence Matrix • An incidence matrix represents the incidence relation between vertices and edges • Put indices from 0, …, n-1 to vertices, and 0, …, m-1 to edges + store edges incident to a vertex to the corresponding row = storing vertices incident to an edge in 0: 0, 1 the corresponding column 1: 1, 5 1 5 5 4 0 2 6 0 1 3 4 2 8 3 7 0: 1, 3 1: 0, 2, 4, 5 2: 1, 3, 4, 5 3: 0, 2 4: 1, 2, 5 5: 1, 2, 4 0: 0, 2 1: 0, 1, 3, 4 2: 4, 6, 7, 8 3: 2, 7 4: 3, 5, 8 5: 1, 5, 6 + 2: 0, 3 3: 1, 4 4: 1, 2 5: 4, 5 6: 2, 5 7: 2, 3 8: 2, 4

Advantage of Incidence Matrix • In the case of incidence matrix, each edge has ID so, easy to handle the attached information to each edge just allocate an array of size m, and it is sufficient • In the case of adjacency matrix, edge doesn’t have ID, thus not easy to manage correspondence of edge and its data • Multiple edges are also easy to handle 1 5 5 4 0 2 6 0 1 3 4 2 8 3 7 0: 1, 3 1: 0, 2, 4, 5 2: 1, 3, 4, 5 3: 0, 2 4: 1, 2, 5 5: 1, 2, 4 0: 0, 2 1: 0, 1, 3, 4 2: 4, 6, 7, 8 3: 2, 7 4: 3, 5, 8 5: 1, 5, 6 + 0: 0, 1 1: 1, 5 2: 0, 3 3: 1, 4 4: 1, 2 5: 4, 5 6: 2, 5 7: 2, 3 8: 2, 4

Allocate Memory for Cells • Incidence matrix can be realized by cells of lists having four links like sparse matrix (two for vertices of the edges, and two for the edges in the vertex) disadvantages of arrays are eliminated • Also can be of two array lists • or, prepare an array and edge i corresponds to 0: 0, 1 cells 2 i and 2 i+1, to represent four links 1: 1, 5 1 5 5 4 0 2 6 0 1 3 4 2 8 3 7 0: 1, 3 1: 0, 2, 4, 5 2: 1, 3, 4, 5 3: 0, 2 4: 1, 2, 5 5: 1, 2, 4 0: 0, 2 1: 0, 1, 3, 4 2: 4, 6, 7, 8 3: 2, 7 4: 3, 5, 8 5: 1, 5, 6 + 2: 0, 3 3: 1, 4 4: 1, 2 5: 4, 5 6: 2, 5 7: 2, 3 8: 2, 4

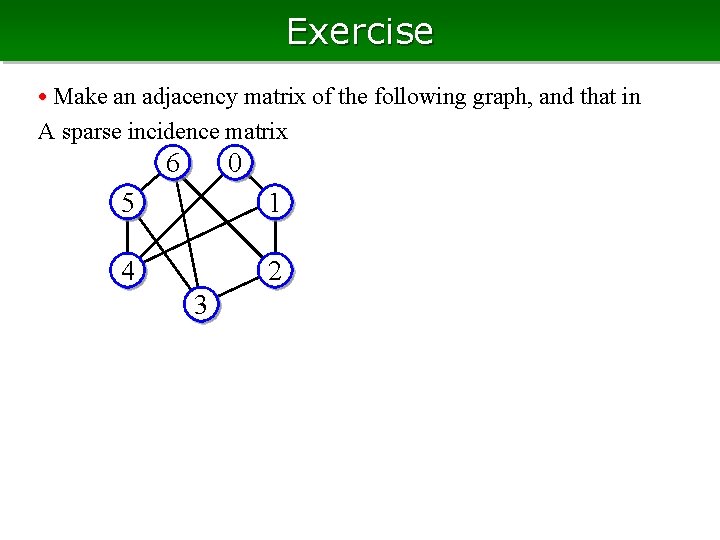
Exercise • Make an adjacency matrix of the following graph, and that in A sparse incidence matrix 6 0 5 1 4 2 3

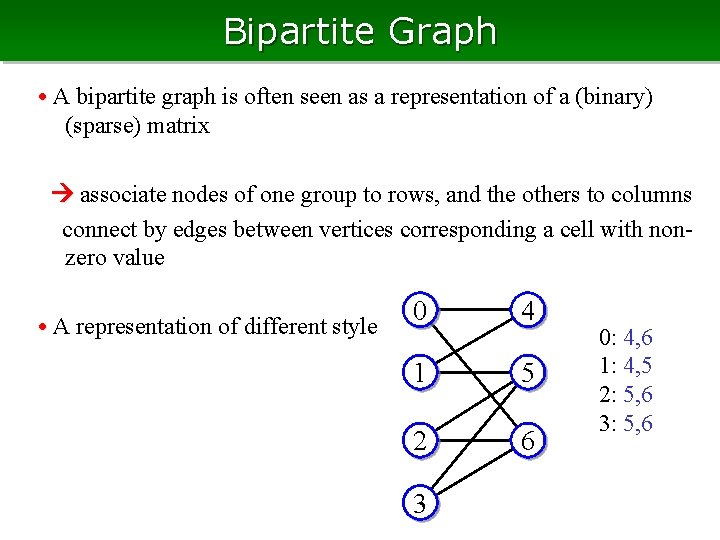
Bipartite Graph • A bipartite graph is often seen as a representation of a (binary) (sparse) matrix associate nodes of one group to rows, and the others to columns connect by edges between vertices corresponding a cell with nonzero value • A representation of different style 0 4 1 5 2 6 3 0: 4, 6 1: 4, 5 2: 5, 6 3: 5, 6

Column: Store Huge Graph • A graph needs two pointer (or integer) per edge weight, and etc. need more • 64 bits are required in 32 bit CPU • However, Web graphs have billion of vertices, and 20 billions of edges 160 GB is necessary in this way • This is too much. Can we reduce the storage size?

Column: Store Huge Graph (2) ① Only few edges have large degrees Vertices are mainly adjacent to these few vertices Put indices so that large degree vertices have small indices, and represent small indices by small number of bits, and large indices by many bits Ex. ) • If the bit sequence representing a number begins with “ 0”, the following 7 bits represent [0 -127] • If “ 10”, the following 14 bits represent 128+[0 -16383] • If “ 11”, the following 30 bits represent 16384+128, …

Column: Store Huge Graph (3) ② Sort the sites in dictionary order of their URLs links are usually to near, thus difference of ID’s becomes small • They can be recorded in the same way, to reduce the space • Using these, one edge needs just 10 bits Further, we can reduce it to 5 bits The storage will be 20 GB, thus can fit recent computers

Summary • Data structures for matrix • Structures for sparse matrix, and four directed lists • Structures for graphs: adjacency matrix and incidence matrix adjacency list