Computer Graphics Chapter 9 Rendering 1 Rendering n

Computer Graphics Chapter 9 Rendering 1

Rendering n RM Three dimensional object rendering is the set of collective processes which make the object model appear more realistic on the display screen. These processes include u The elimination of surfaces (polygonal segments) on the object that are not visible with respect to the user’s view direction. u Incorporating shading and shadowing effects. 2

Computing Surface Normal V 1 = P 2 P 1 = (x 2 x 1, y 2 y 1, z 2 z 1). V 2 = P 3 P 1 = (x 3 x 1, y 3 y 1, z 3 z 1). N = V 1 V 2. Surface Normal: RM 3

Components of Surface Normal Nx = (y 2 y 1) (z 3 z 1) (y 3 y 1) (z 2 z 1) Ny = (z 2 z 1) (x 3 x 1) (z 3 z 1) (x 2 x 1) Nz = (x 2 x 1) (y 3 y 1) (x 3 x 1) (y 2 y 1) OR Nx = y 1(z 2 -z 3)+ y 2(z 3 -z 1)+ y 3(z 1 -z 2) Ny = z 1(x 2 -x 3)+ z 2(x 3 -x 1)+ z 3(x 1 -x 2) Nz = x 1(y 2 -y 3)+ x 2(y 3 -y 1)+ x 3(y 1 -y 2) RM 4

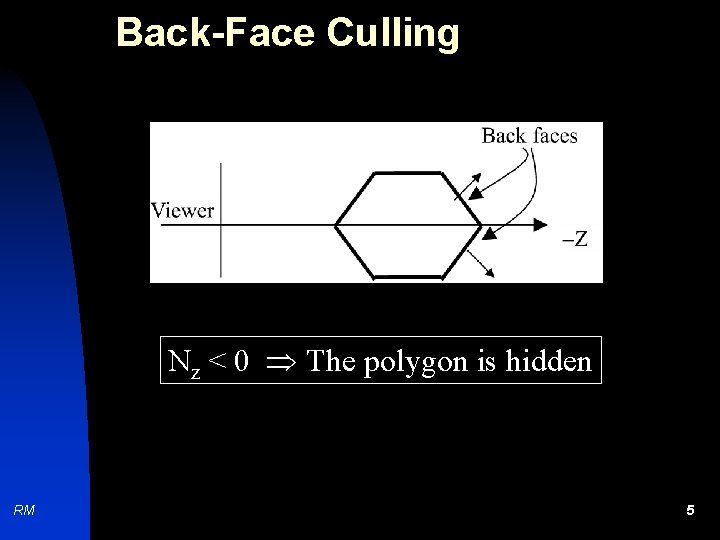
Back-Face Culling Nz < 0 The polygon is hidden RM 5

Back-Face Culling Limitations n n n RM Requires specific ordering of the vertices in the polygon table to determine the outward normal direction. The algorithm will work only with convex objects. A polygon is either completely displayed, or totally eliminated from the display. 6

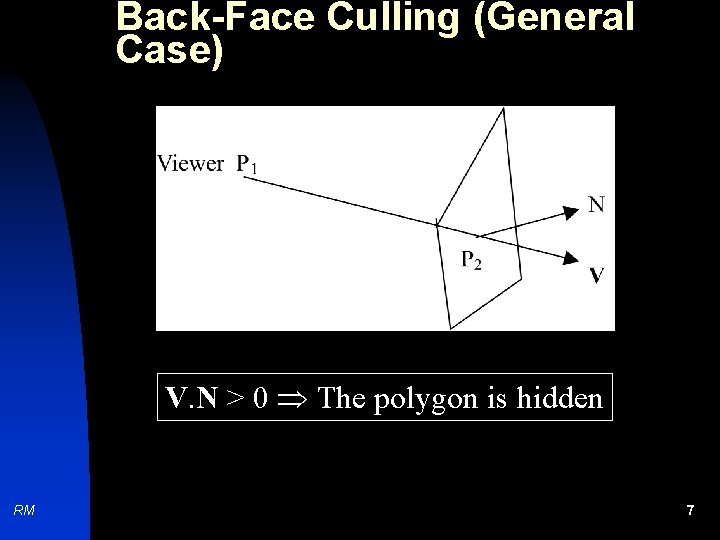
Back-Face Culling (General Case) V. N > 0 The polygon is hidden RM 7

Back-Face Culling (Example) RM 8

Back-Face Culling (Open. GL) RM 9

Painter’s Algorithm RM 10

Painters Algorithm n Basic Steps: u Sort polygons in the ascending order of z-coordinates u Fill RM polygons in the sorted order. 11

Painters Algorithm Limitations n Requires sorting of polygons. n All polygons must be necessarily filled. n RM May lead to erroneous images if a failure condition (see below) occurs. 12

Painters Algorithm Failure Conditions (1) Polygons with depth and region overlap. (1) Z (2) RM Polygons having both depth-overlap and region overlap may require re-sequencing of the polygons in the sorted list. 13

Painters Algorithm Failure Conditions (2) Polygons with cyclic overlap. RM 14

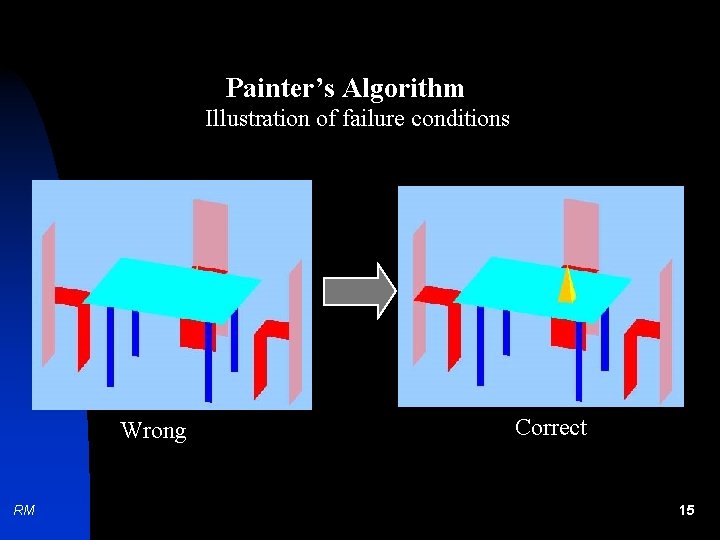
Painter’s Algorithm Illustration of failure conditions Wrong RM Correct 15

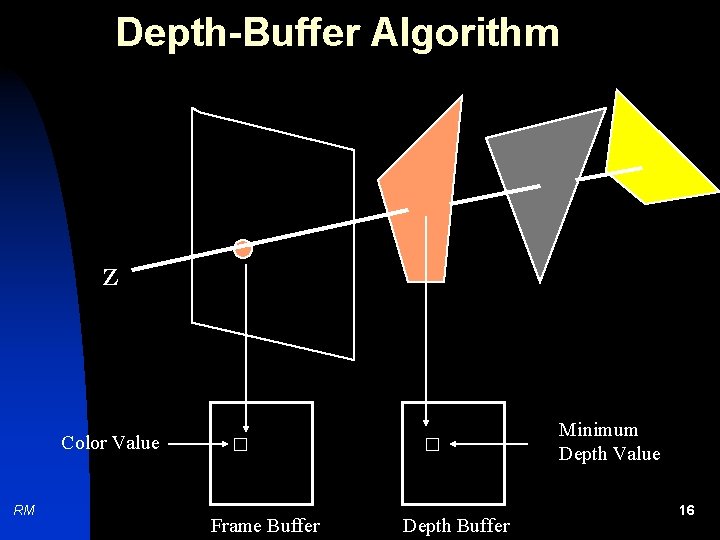
Depth-Buffer Algorithm Z Minimum Depth Value Color Value RM Frame Buffer Depth Buffer 16

Depth-Buffer Algorithm n n n RM For each pixel (i, j), a line passing through the pixel and the viewer is considered, and the depths of the polygons on this line are computed. The value d(i, j) in the depth buffer contains the pseudo-depth of the closest polygon encountered at pixel (i, j). The value p(i, j) in the frame buffer (the color of the pixel) is the color of the closest polygon. 17

Depth-Buffer Algorithm n RM Limitations: u The algorithm requires a large amount of additional memory to store the pseudo depth at each pixel value. u Since the analysis is based on a point by point test, the algorithm is time consuming. 18

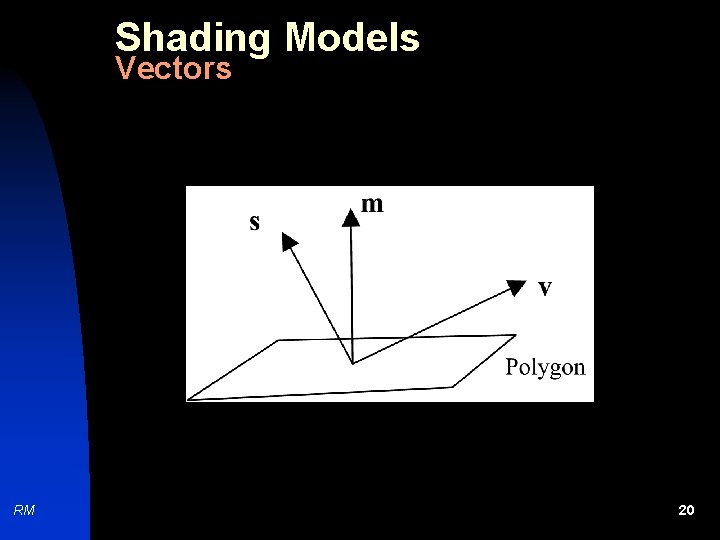
Shading Models n n n A shading model dictates how light is scattered or reflected from a surface. A surface is shaded by adjusting the color intensity value of each polygon according to the shading algorithm. Main components: Light source vector, surface normal vector, viewer direction. u Material characteristics of the surface u The illumination model. u RM 19

Shading Models Vectors RM 20

Shading Models Surface Properties (1) n abs (Coeff. of absorption): Specifies how much of the incident light is absorbed. If all of the incident light is absorbed, the object appears black. n spec (Coeff. of specular reflection) Specifies how much of the incident light is specularly reflected in one direction. For a highly reflective surface such as a mirror, the value is close to 1. 0 RM 21

Shading Models Surface Properties (2) n diff (Coeff. of diffuse reflection): Diffuse scattering occurs when the incident light is re-radiated uniformly in all directions. For a rough non-reflective surface, the value is close to 1. 0. n amb (Coeff. of ambient reflection): Specifies how much of the ambient light is reflected by the surface. Often this is same as the diffuse reflection coefficient diff. abs + spec + diff = 1. 0 RM 22

Surface Properties I If I is the incident light intensity, then I abs is absorbed by the surface. I spec is specularly reflected. I diff is diffusely reflected. RM 23

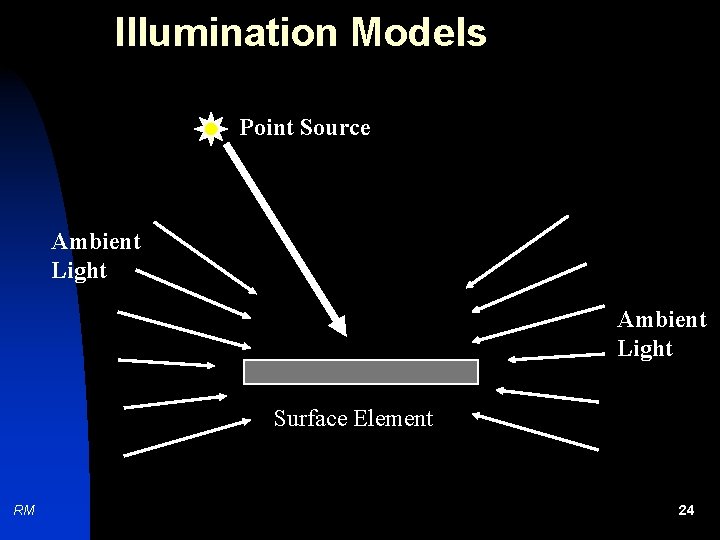
Illumination Models Point Source Ambient Light Surface Element RM 24

Illumination Models Ambient Light n n RM Produces uniform illumination (also known as background light). Has no spatial or directional characteristics. Assumed to be incident from all directions with constant intensity Ia. Ambient light reflection from a surface is constant along all visible directions, and does not depend on the surface orientation. 25

Illumination Models Point Light Source n n n RM Defined in terms of both the position of the source, and the intensity of the source Is. The reflection from a point light source depends on the surface orientation, and varies with respect to the view direction. Light source reflection consists of both specular reflection and diffuse reflection. 26

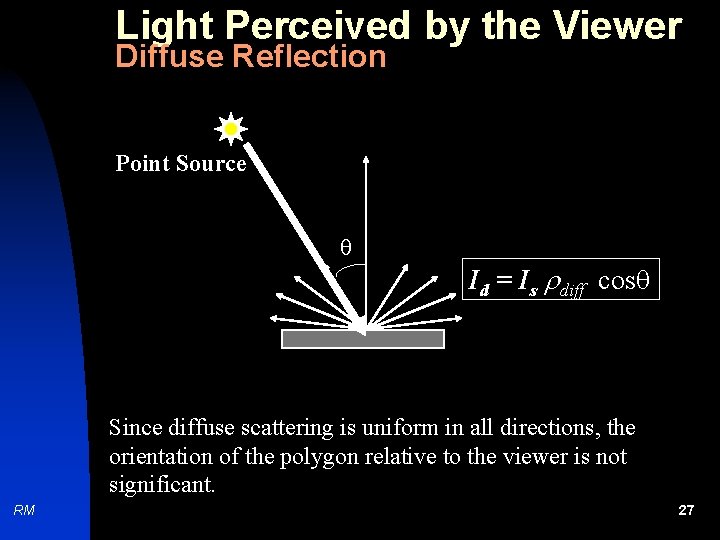
Light Perceived by the Viewer Diffuse Reflection Point Source Id = Is diff cos Since diffuse scattering is uniform in all directions, the orientation of the polygon relative to the viewer is not significant. RM 27

Light Perceived by the Viewer Specular Reflection Isp = (Is spec cos f ) The vector h = s + v is known as the half-way vector. RM f is an experimentally determined constant 28

Light Perceived by the Viewer Specular Reflection f is specular reflection parameter determine type of surface. (in Open. GL the value range 0 to 128). A very shiny surface is modeled with a large value, and smaller value (down to 0) are used for dull object. RM 29

Light Perceived by the Viewer Ambient Reflection n Ambient reflection is independent of surface orientation. Ambient reflection is independent of viewers position. The ambient light Ia is uniformly reflected with intensity Ia amb. This is denoted as the ambient reflection Iamb = Ia amb RM 30

Computation of Total Reflected Light Total light intensity perceived by the user = Iamb+ Isp + Id = (Ia amb) + (Is spec cos f ) + Is diff cos RM 31

Shading (Open. GL) RM 32

Flat and Smooth Shading Flat Shading The entire polygon is drawn with the same shade or color. RM Gouraud Shading The shades at the vertices are interpolated to determine the shade at an interior point 33

Gouraud Shading n n n RM The color at P 1 is obtained by linearly interpolating the colors C 1 and C 2. Similarly, the color at P 2 is found by linearly interpolating the colors C 3 and C 4. Having found P 1 and P 2, the algorithm then fills along the scan line by linearly interpolating between P 1 and P 2 to determine the color at an intermediate pixel Q. 34

Flat and Smooth Shading (Open. GL) RM 35

Flat and Smooth Shading Flat Shading Gouraud shading provides a much smoother appearance of surfaces. RM 36

Texture Mapping (Examples) RM 37

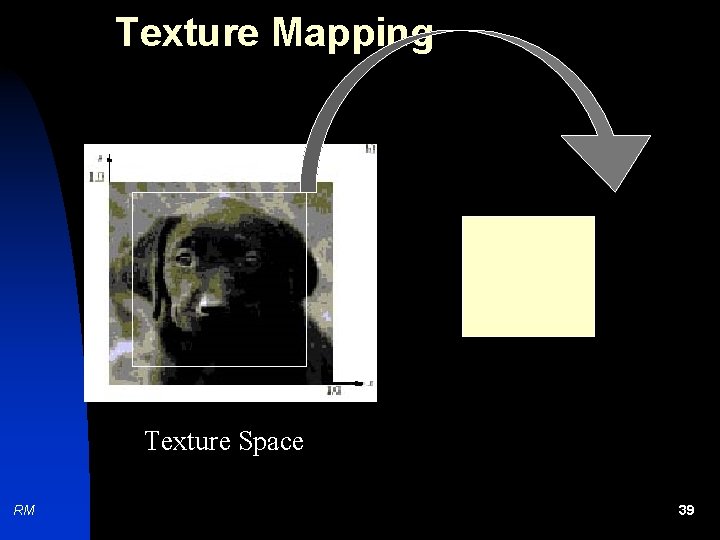
Texture Mapping n n n RM The basic techniques begin with some texture functions, texture(s, t), in texture space which is traditionally marked off by parameters named s and t. The function texture(s, t) produces a color or intensity value for each value of s and t between 0 and 1. Texture mapping is the process of mapping a region in the 2 D texture space to a region in the 3 D space defined by the boundary points. 38

Texture Mapping Texture Space RM 39

Texture Mapping (Open. GL) RM 40

Texture types n n RM Bitmap Textures: Often formed from bitmap representations of images. Defined by a mathematical function or procedure. 41