MultipleView Geometry for Image Based Modeling Course 42

Multiple-View Geometry for Image. Based Modeling (Course 42) Lecturers: Yi Ma (UIUC) Stefano Soatto (UCLA) Jana Kosecka (GMU) Rene Vidal (UC Berkeley) Yizhou Yu (UIUC)

COURSE LECTURE OUTLINE A. Introduction (Ma) B. Preliminaries: geometry & image formation (Ma) C. Image primitives & correspondence (Soatto) D. Two calibrated views (Kosecka) E. Uncalibrated geometry and stratification (Soatto) F. Multiple-view geometry & algebra (Vidal, Ma) G. Reconstruction from scene knowledge (Ma) H. Step-by-step building of 3 D model (Kosecka, Soatto) I. Image-based texture mapping and rendering (Yu)

Multiple-View Geometry for Image-Based Modeling Introduction (Lecture A) Yi Ma Perception & Decision Laboratory Decision & Control Group, CSL Image Formation & Processing Group, Beckman Electrical & Computer Engineering Dept. , UIUC http: //decision. csl. uiuc. edu/~yima

IMAGES AND GEOMETRY – A Little History of Perspective Imaging • Pinhole (perspective) imaging, in most ancient civilizations. • Euclid, perspective projection, 4 th century B. C. , Alexandria • Pompeii frescos, 1 st century A. D. Image courtesy of C. Taylor

IMAGES AND GEOMETRY – A Little History of Perspective Imaging • Fillippo Brunelleschi, first Renaissance artist painted with correct perspective, 1413 • “Della Pictura”, Leone Battista Alberti, 1435 • Leonardo Da Vinci, stereopsis, shading, color, 1500 s • “The scholar of Athens”, Raphael, 1518 Image courtesy of C. Taylor

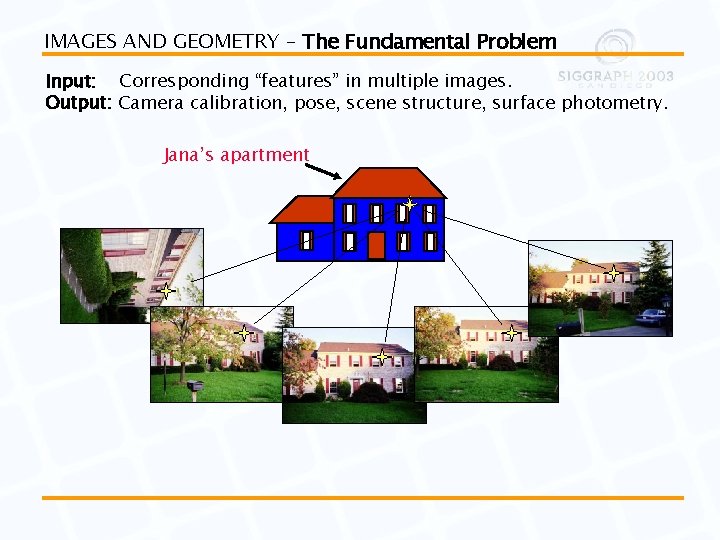
IMAGES AND GEOMETRY – The Fundamental Problem Input: Corresponding “features” in multiple images. Output: Camera calibration, pose, scene structure, surface photometry. Jana’s apartment

IMAGES AND GEOMETRY – History of “Modern” Geometric Vision • Chasles, formulated the two-view seven-point problem, 1855 • Hesse, solved the above problem, 1863 • Kruppa, solved the two-view five-point problem, 1913 • Longuet-Higgins, the two-view eight-point algorithm, 1981 • Liu and Huang, the three-view trilinear constraints, 1986 • Huang and Faugeras, SVD based eight-point algorithm, 1989 • Tomasi and Kanade, (orthographic) factorization method, 1992 • Ma, Huang, Kosecka, Vidal, multiple-view rank condition, 2000

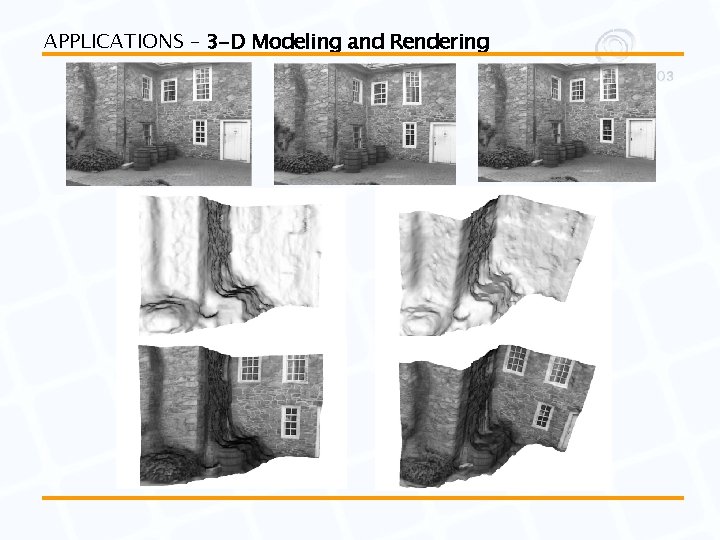
APPLICATIONS – 3 -D Modeling and Rendering

APPLICATIONS – 3 -D Modeling and Rendering Image courtesy of Paul Debevec

APPLICATIONS – Image Morphing, Mosaicing, Alignment Images of CSL, UIUC

APPLICATIONS – Real-Time Sports Coverage First-down line and virtual advertising Image courtesy of Princeton Video Image, Inc.

APPLICATIONS – Real-Time Virtual Object Insertion UCLA Vision Lab

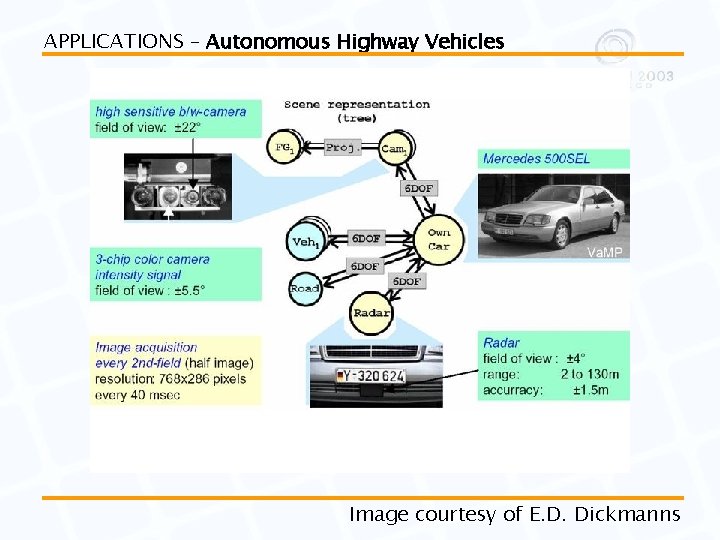
APPLICATIONS – Autonomous Highway Vehicles Image courtesy of E. D. Dickmanns

APPLICATIONS – Unmanned Aerial Vehicles (UAVs) Rate: 10 Hz Accuracy: 5 cm, 4 o Berkeley Aerial Robot (BEAR) Project

Multiple-View Geometry for Image-Based Modeling Preliminaries: Imaging Geometry & Image Formation (Lecture B) Yi Ma Perception & Decision Laboratory Decision & Control Group, CSL Image Formation & Processing Group, Beckman Electrical & Computer Engineering Dept. , UIUC http: //decision. csl. uiuc. edu/~yima

Preliminaries: Imaging Geometry and Image Formation INTRODUCTION 3 D EUCLIDEAN SPACE & RIGID-BODY MOTION • Coordinates and coordinate frames • Rigid-body motion and homogeneous coordinates GEOMETRIC MODELS OF IMAGE FORMATION • Lens & Lambertian surfaces • Pinhole camera model CAMERA INTRINSIC PARAMETERS & RADIAL DISTORTION • From space to pixel coordinates • Notation: image, preimage, and coimage • Radial distortion and correction SUMMARY OF NOTATION

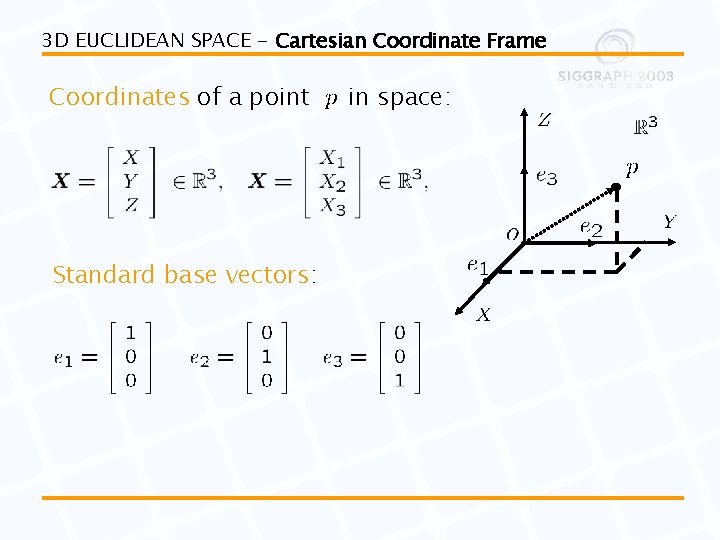
3 D EUCLIDEAN SPACE - Cartesian Coordinate Frame Coordinates of a point Standard base vectors: in space:

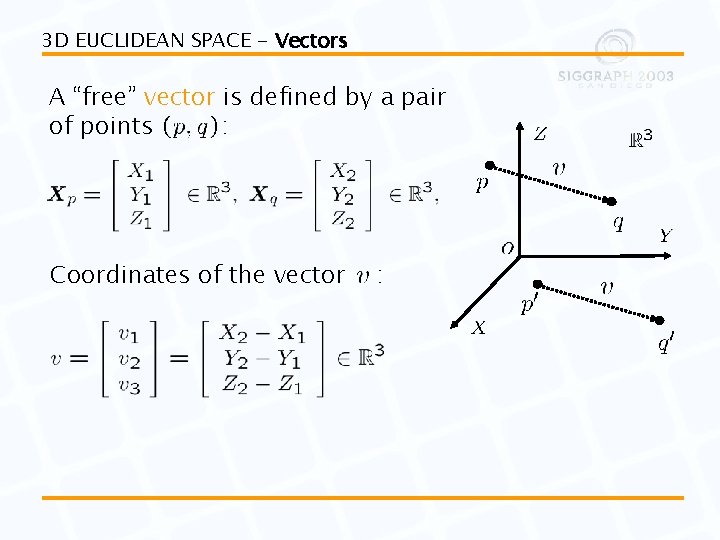
3 D EUCLIDEAN SPACE - Vectors A “free” vector is defined by a pair of points : Coordinates of the vector :

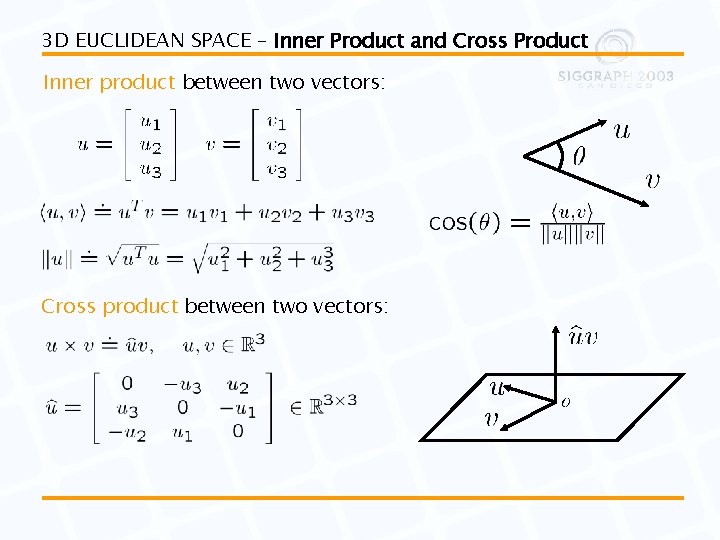
3 D EUCLIDEAN SPACE – Inner Product and Cross Product Inner product between two vectors: Cross product between two vectors:

RIGID-BODY MOTION – Rotation matrix: Coordinates are related by:

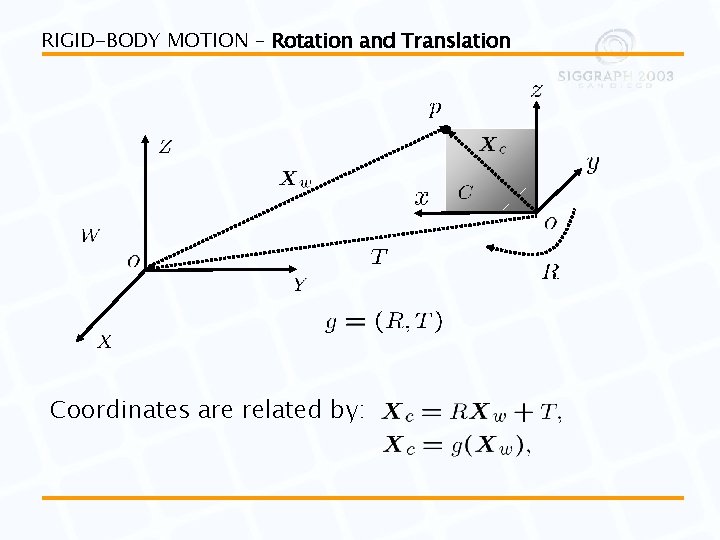
RIGID-BODY MOTION – Rotation and Translation Coordinates are related by:

RIGID-BODY MOTION – Homogeneous Coordinates 3 D coordinates are related by: Homogeneous coordinates are related by: Homogeneous coordinates of a vector:

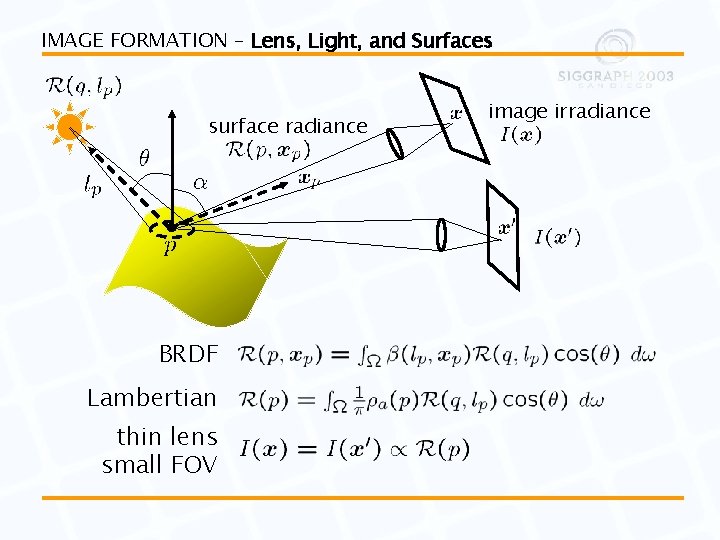
IMAGE FORMATION – Lens, Light, and Surfaces surface radiance BRDF Lambertian thin lens small FOV image irradiance

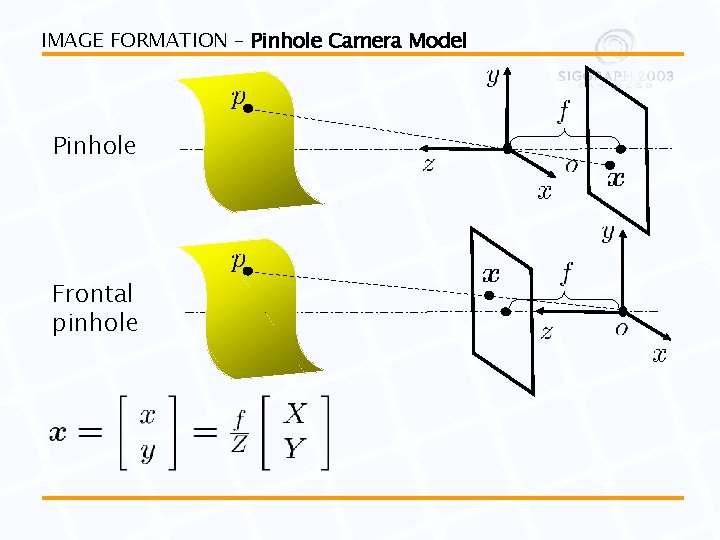
IMAGE FORMATION – Pinhole Camera Model Pinhole Frontal pinhole

IMAGE FORMATION – Pinhole Camera Model 2 D coordinates Homogeneous coordinates

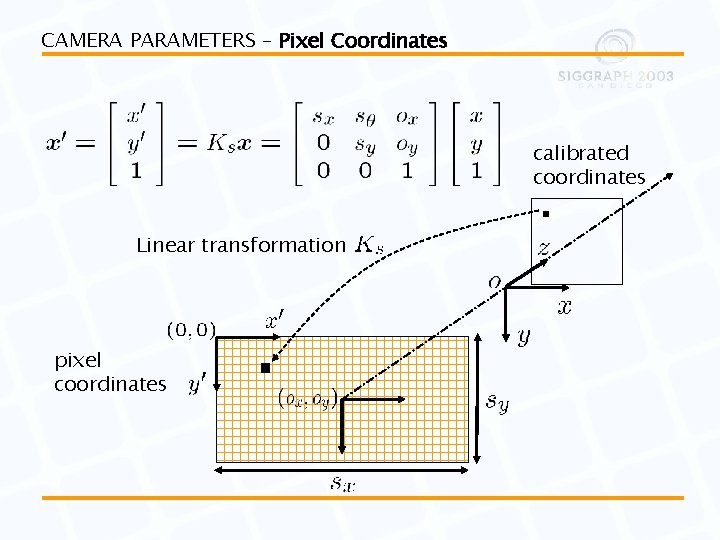
CAMERA PARAMETERS – Pixel Coordinates calibrated coordinates Linear transformation pixel coordinates

CAMERA PARAMETERS – Calibration Matrix and Camera Model Ideal pinhole Calibration matrix (intrinsic parameters) Projection matrix Camera model Pixel coordinates

CAMERA PARAMETERS – Radial Distortion Nonlinear transformation along the radial direction Distortion correction: make lines straight

IMAGE FORMATION – Image of a Point Homogeneous coordinates of a 3 -D point Homogeneous coordinates of its 2 -D image Projection of a 3 -D point to an image plane

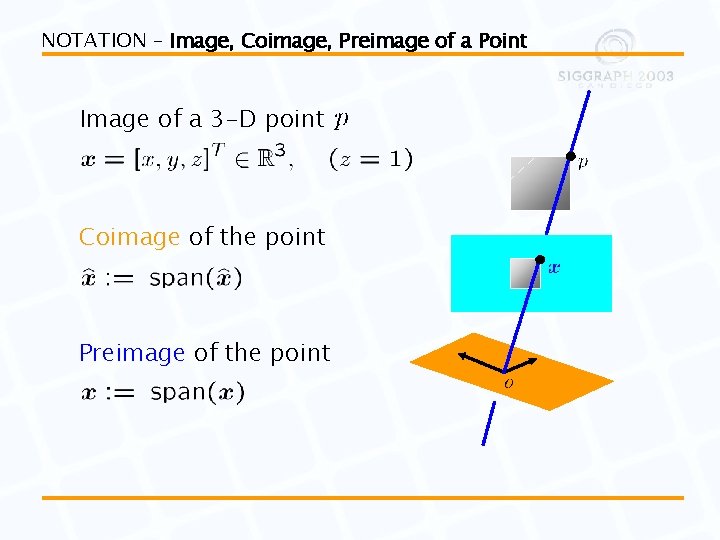
NOTATION – Image, Coimage, Preimage of a Point Image of a 3 -D point Coimage of the point Preimage of the point

NOTATION – Image, Coimage, Preimage of a Line Coimage of a 3 -D line Preimage of the line Image of the line

IMAGE FORMATION – Coimage of a Line Homogeneous representation of a 3 -D line Homogeneous representation of its 2 -D coimage Projection of a 3 -D line to an image plane

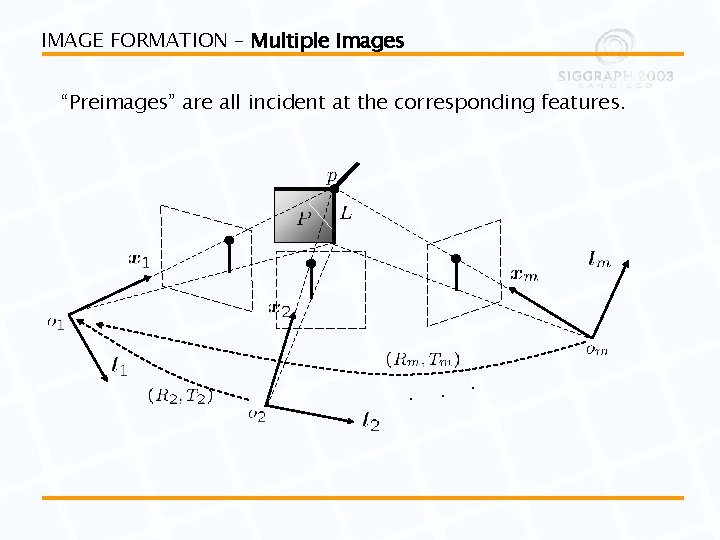
IMAGE FORMATION – Multiple Images “Preimages” are all incident at the corresponding features. .

LIST OF REFERENCES Chapters 2 & 3 An Invitation to 3 -D Vision: From Images to Geometric Models, Ma, Soatto, Kosecka, Sastry, Springer-Verlag, 2003.